Solving Differential Equations Solving Differential Equations A differential





















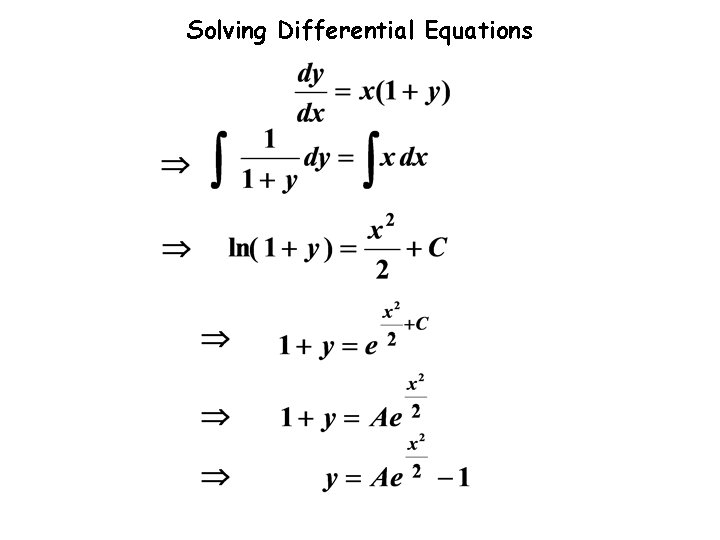

- Slides: 29

Solving Differential Equations

Solving Differential Equations A differential equation is an equation which contains a derivative such as or . Solving a differential equation means finding an expression for y in terms of x or for A in terms of t without the derivative. e. g. (1) e. g. (2) To solve (1) we just integrate with respect to x. However, we can’t integrate y w. r. t. x so (2) needs another method.

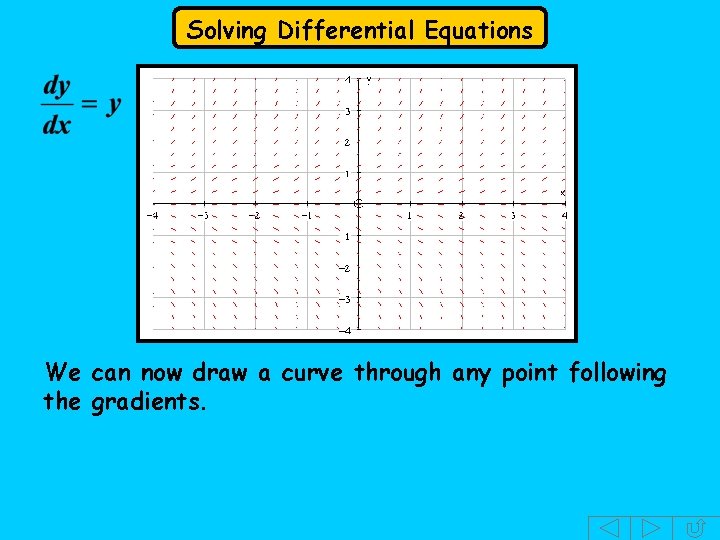
Solving Differential Equations e. g. (2) Before we see how to solve the equation, it’s useful to get some idea of the solution. The equation tells us that the graph of y has a gradient that always equals y. We can sketch the graph by drawing a gradient diagram. For example, at every point where y = 2, the 2 gradient equals 2. We can 1 draw a set of small lines showing this gradient. We can cover the page with similar lines.

Solving Differential Equations We can now draw a curve through any point following the gradients.

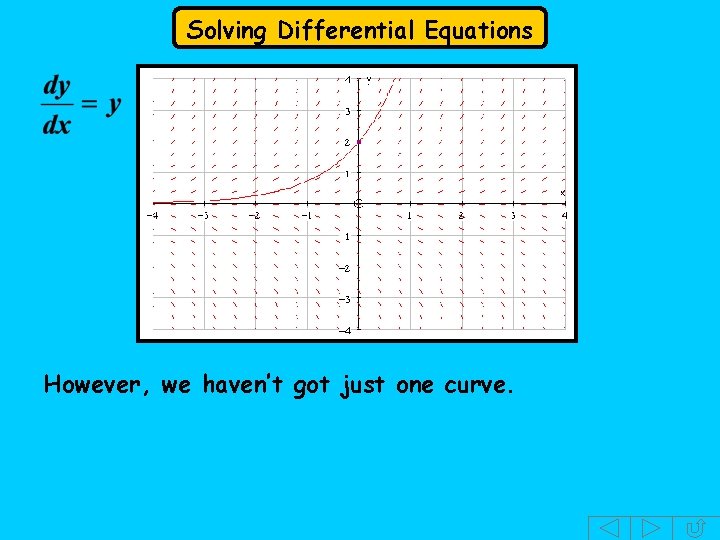
Solving Differential Equations However, we haven’t got just one curve.

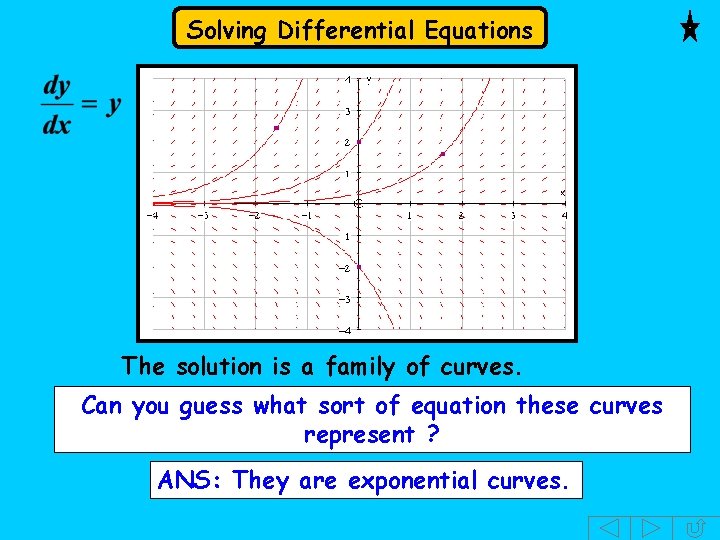
Solving Differential Equations The solution is a family of curves. Can you guess what sort of equation these curves represent ? ANS: They are exponential curves.

Solving Differential Equations Solving We use a method called “ Separating the Variables” and the title describes exactly what we do. We rearrange so that x terms are on the right and y on the left. Multiply by dx and divide by y. Now insert integration signs. . . and integrate We can separate the 2 parts of the derivative because although it isn’t actually a fraction, it behaves like one. We l. h. s. don’t need a constant on both sides theyw. r. t. x) (the is integrated w. r. t. y and the as r. h. s. can be combined. I usually put it on the r. h. s.

Solving Differential Equations We’ve now solved the differential equation to find the general solution but we have an implicit equation and we often want it to be explicit ( in the form y =. . . ) A log is just an index, so ( We now have the exponential that we spotted from the gradient diagram. ) However, it can be simplified.

Solving Differential Equations We can write as. Since is a constant it can be replaced by a single letter, k. So, This is usually written as positive or negative. where k is positive where A is So, In this type of example, because the result is valid for positive and negative values, I usually use A directly when I change from log to exponential form.

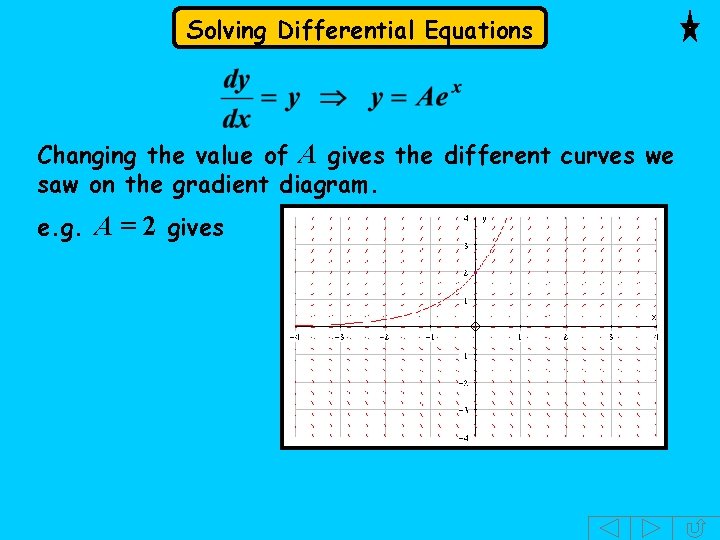
Solving Differential Equations Changing the value of A gives the different curves we saw on the gradient diagram. e. g. A = 2 gives

Solving Differential Equations The differential equation is important as it is one of a group used to model actual situations. These are situations where there is exponential growth or decay. We will investigate them further in the next presentation. We will now solve some other equations using the method of separating the variables.

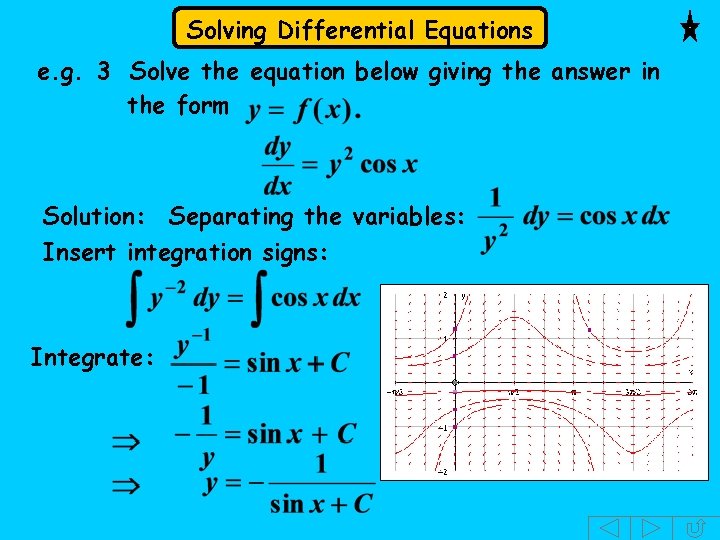
Solving Differential Equations e. g. 3 Solve the equation below giving the answer in the form Solution: Separating the variables: Insert integration signs: Integrate:

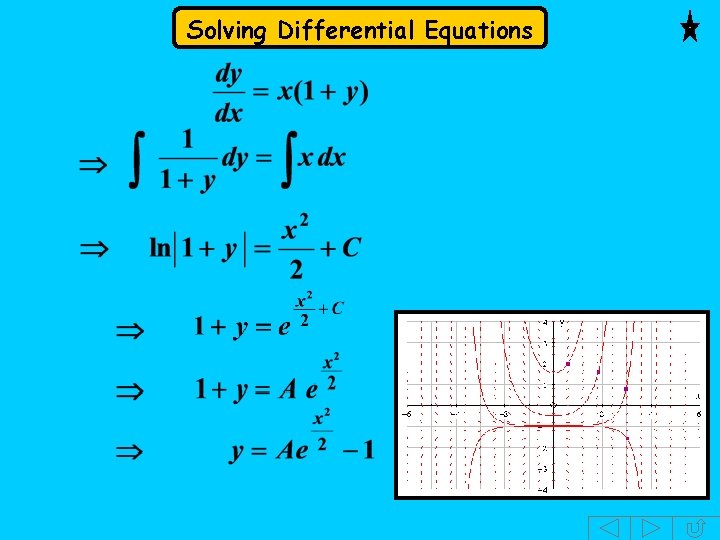
Solving Differential Equations e. g. 4 Solve the equation below giving the answer in the form Solution: It’s no good dividing by y as this would give which is no help. Instead, we take out x as a common factor on the r. h. s. , so We can now separate the variables by dividing by

Solving Differential Equations

Solving Differential Equations You may sometimes see this written as

Solving Differential Equations

Solving Differential Equations • • SUMMARY Some differential equations can be solved by separating the variables. To use the method we need to be able to write the equation in the form ( If the equation has a total of 3 terms we will need to bracket 2 together before separating the variables. ) • The l. h. s. is integrated w. r. t. y and the r. h. s. w. r. t. x, so • • The answer is often written explicitly. The solution is called the general solution.

Exercise Solving Differential Equations 1. Find the general solutions of the following equations giving your answers in the form : (a) (b) 2. Find the general solutions of the following equations leaving the answers in implicit form: (a) b) 3. Find the equation of the curve given by the following equation and which passes through the given point. ( This is called a particular solution. )

Solving Differential Equations Solutions: (b)

Solving Differential Equations 2(a) b)

Solving Differential Equations 3. You might prefer to write separate the variables. or as before you

Solving Differential Equations

Solving Differential Equations The following slides contain repeats of information on earlier slides, shown without colour, so that they can be printed and photocopied. For most purposes the slides can be printed as “Handouts” with up to 6 slides per sheet.

Solving Differential Equations e. g. 1 Solving We use a method called “ Separating the Variables” and the title describes exactly what we do. We rearrange so that x terms are on the right and y on the left. Multiply by dx and divide by y. Now insert integration signs. . . and integrate (the l. h. s. is integrated w. r. t. y and the r. h. s. w. r. t. x)

Solving Differential Equations We’ve now solved the differential equation to find the general solution but we have an implicit equation and we often want it to be explicit ( in the form y =. . . ) A log is just an index, so This can be simplified. We can write as. Since is a constant it can be replaced by a single letter. We usually use A. So,

Solving Differential Equations e. g. 2 Solve the equation below giving the answer in the form Solution: Separating the variables: Insert integration signs: Integrate:

Solving Differential Equations e. g. 3 Solve the equation below giving the answer in the form Solution: It’s no good dividing by y as this would give which is no help. Instead, we take out x as a common factor on the r. h. s. We can now separate the variables by dividing by
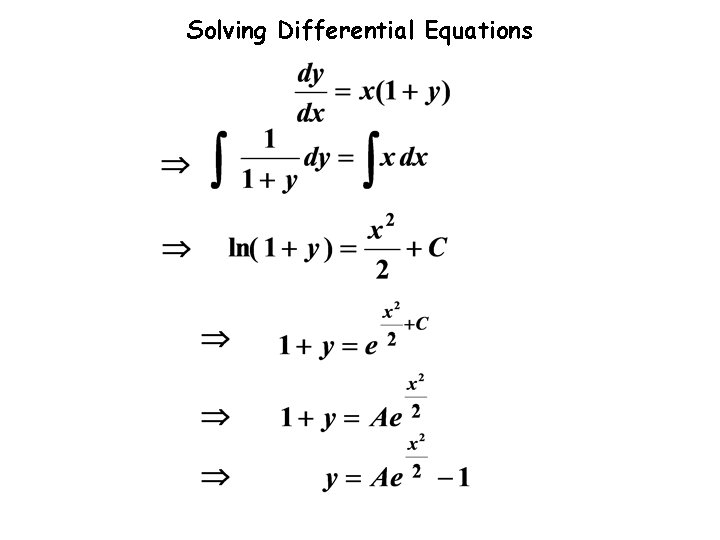
Solving Differential Equations

Solving Differential Equations • • SUMMARY Some differential equations can be solved by separating the variables. To use the method we need to be able to write the equation in the form ( If the equation has a total of 3 terms we will need to bracket 2 together before separating the variables. ) • The l. h. s. is integrated w. r. t. y and the r. h. s. w. r. t. x, so • • The answer is often written explicitly. The solution is called the general solution.