Modeling and Simulation of Genetic Regulatory Networks using

Modeling and Simulation of Genetic Regulatory Networks using Ordinary Differential Equations Hidde de Jong Projet HELIX Institut National de Recherche en Informatique et en Automatique Unité de Recherche Rhône-Alpes 655, avenue de l’Europe Montbonnot, 38334 Saint Ismier CEDEX Email: Hidde. de-Jong@inrialpes. fr

Overview 1. Analysis of genetic regulatory networks 2. Approaches towards modeling and simulation of genetic regulatory networks l overview l nonlinear differential equations l piecewise-linear differential equations 4. Discussion: towards virtual cells 2

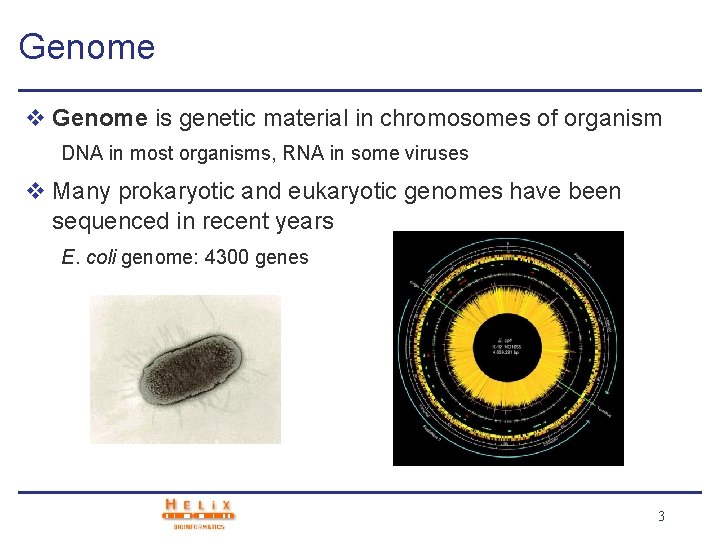
Genome v Genome is genetic material in chromosomes of organism DNA in most organisms, RNA in some viruses v Many prokaryotic and eukaryotic genomes have been sequenced in recent years E. coli genome: 4300 genes 3

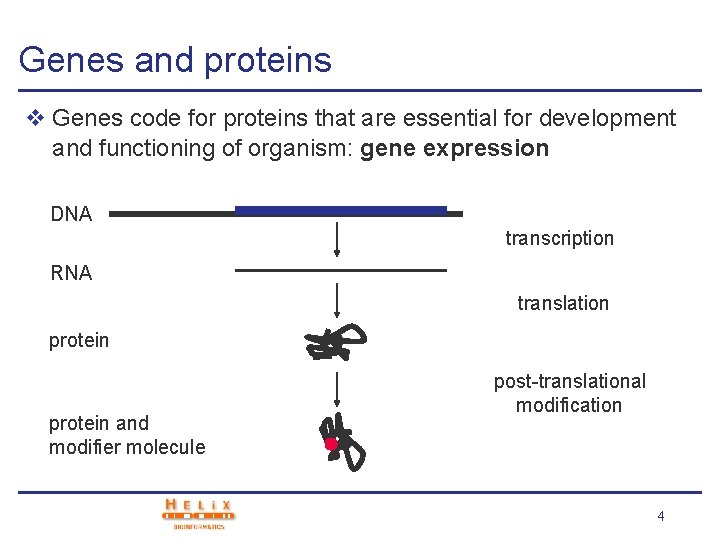
Genes and proteins v Genes code for proteins that are essential for development and functioning of organism: gene expression DNA transcription RNA translation protein and modifier molecule post-translational modification 4

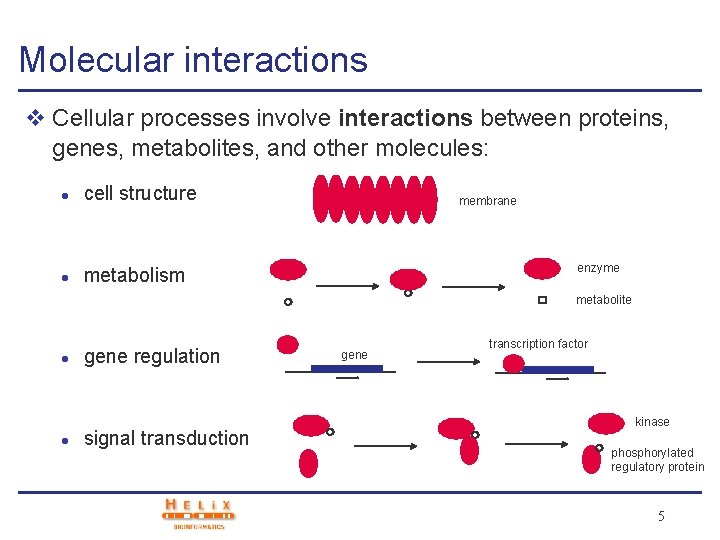
Molecular interactions v Cellular processes involve interactions between proteins, genes, metabolites, and other molecules: l cell structure l metabolism membrane enzyme metabolite l l gene regulation signal transduction gene transcription factor kinase phosphorylated regulatory protein 5

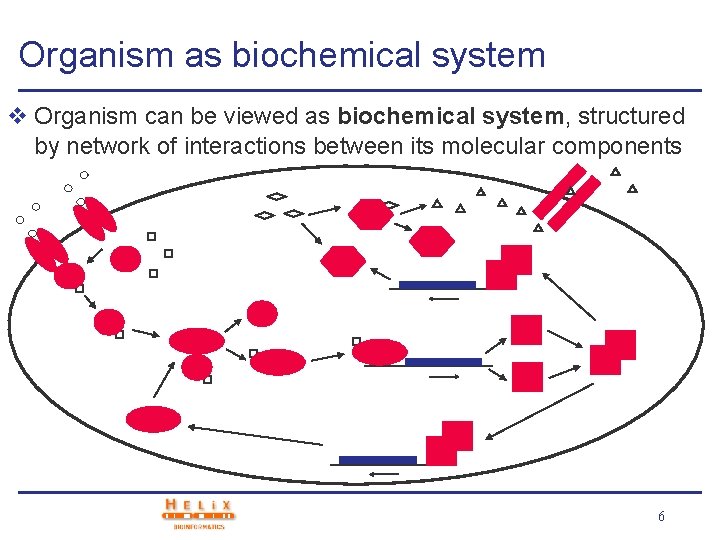
Organism as biochemical system v Organism can be viewed as biochemical system, structured by network of interactions between its molecular components 6

Systems biology v Challenge of systems biology: understand how global behavior of organism emerges from local interactions between its molecular components "A transition is occurring in biology from the molecular level to the system level that promises to revolutionize our understanding of complex biological regulatory systems. . . " Kitano (2002), Science, 295(5560): 564 v Elements of systems biology: l High-throughput experimental techniques l Advanced computational techniques and powerful computers l Integrated application of experimental and computational tools 7

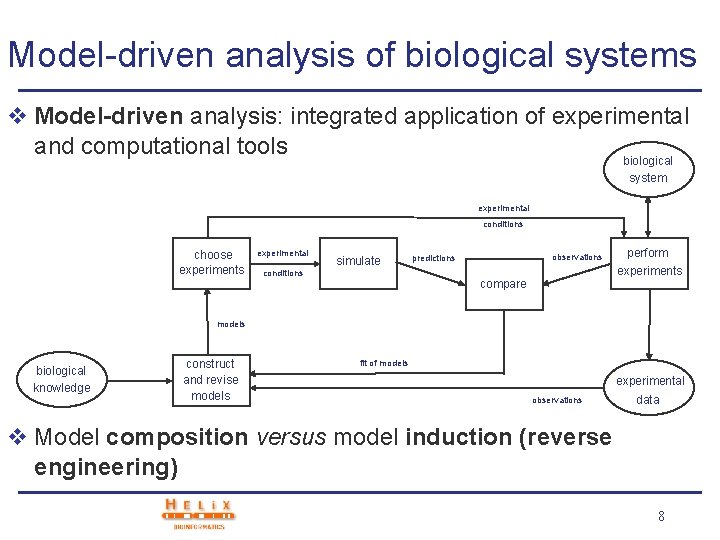
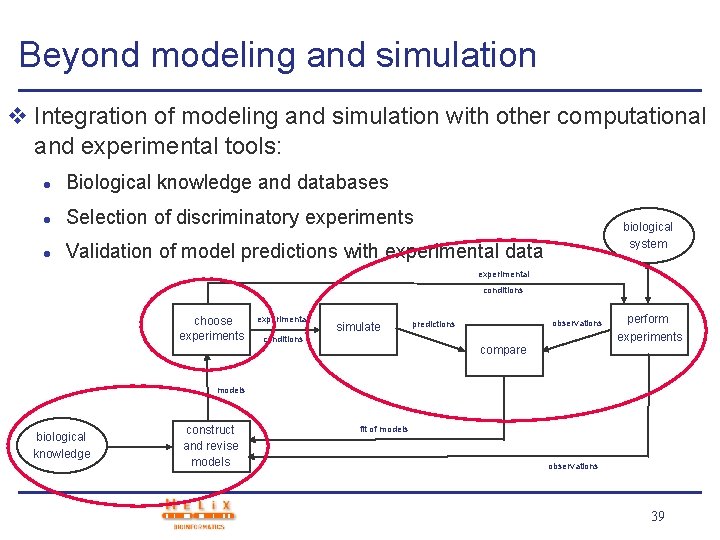
Model-driven analysis of biological systems v Model-driven analysis: integrated application of experimental and computational tools biological system experimental conditions choose experiments experimental simulate conditions observations predictions compare perform experiments models biological knowledge construct and revise models fit of models experimental observations data v Model composition versus model induction (reverse engineering) 8

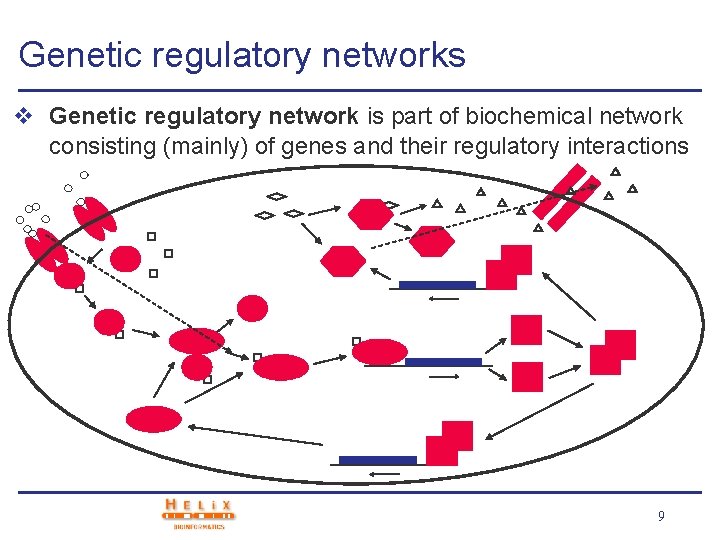
Genetic regulatory networks v Genetic regulatory network is part of biochemical network consisting (mainly) of genes and their regulatory interactions 9

Experimental tools v Study of large and complex genetic regulatory networks requires powerful experimental tools High-throughput, low-cost, reliable, precise v Information obtained from experimental tools in genomics: l DNA sequence (genes) of organism l interactions between proteins and DNA (microarrays) l temporal variation of gene products (microarrays, mass spectometry) 10

Computational tools v Computer support indispensable for dynamical analysis of genetic regulatory networks: modeling and simulation l precise and unambiguous description of network l systematic derivation of behavior predictions v First models of genetic regulatory networks date back to early days of molecular biology Regulation of lac operon (Jacob and Monod) Goodwin (1963), Temporal Organization in Cells v Variety of modeling formalisms exist… de Jong (2002), J. Comput. Biol. , 9(1): 69 -105 Hasty et al. (2001), Nat. Rev. Genet. , 2(4): 268 -279 Smolen et al. (2000), Bull. Math. Biol. , 62(2): 247 -292 11

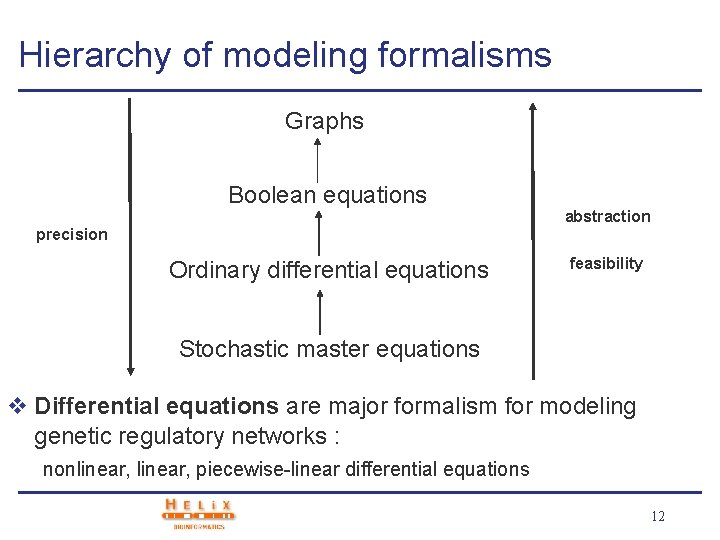
Hierarchy of modeling formalisms Graphs Boolean equations abstraction precision Ordinary differential equations feasibility Stochastic master equations v Differential equations are major formalism for modeling genetic regulatory networks : nonlinear, piecewise-linear differential equations 12

Nonlinear differential equation models v Cellular concentration of proteins, m. RNAs, and other molecules at time-point t represented by continuous variable xi(t) R 0 v Regulatory interactions modeled by differential equations dx. x f (x), dt where x [x 1, …, xn]´and f (x) is nonlinear rate law v No analytical solution for most nonlinear differential equations v Approximation of solution obtained by numerical simulation, given parameter values and initial conditions x(0) x 0 13

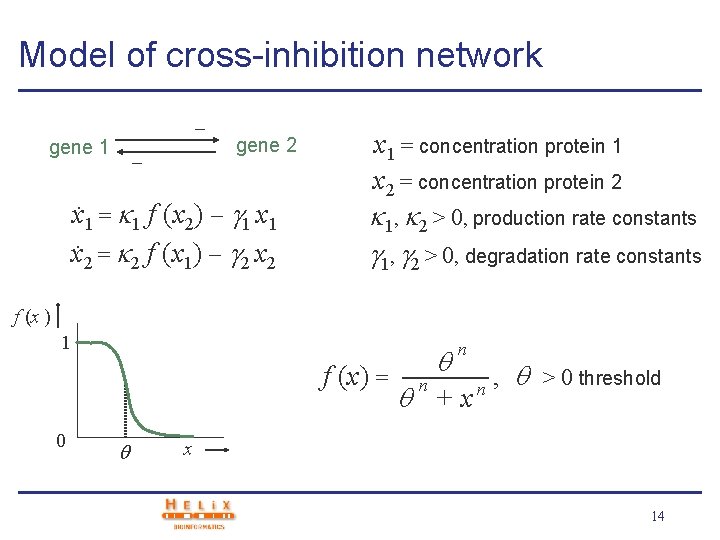
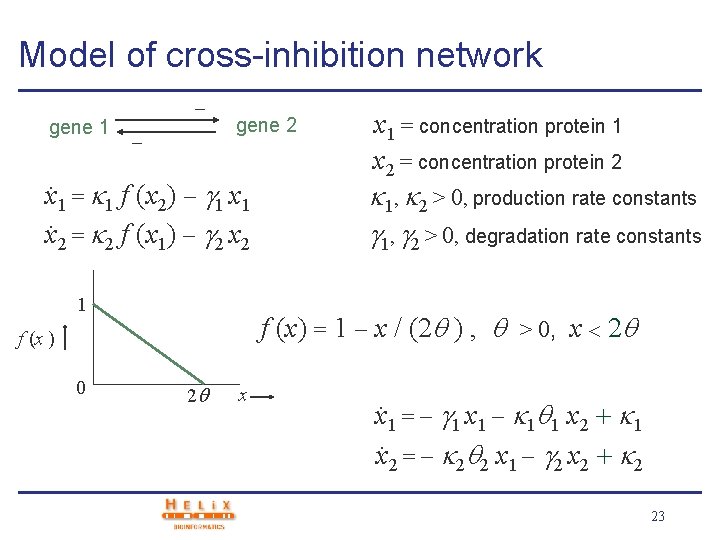
Model of cross-inhibition network gene 1 gene 2 x. 1 = 1 f (x 2) 1 x. 2 = 2 f (x 1) 2 x 1 = concentration protein 1 x 2 = concentration protein 2 1, 2 > 0, production rate constants 1, 2 > 0, degradation rate constants f (x ) 1 f (x) = 0 n n +x n , > 0 threshold x 14

Phase-plane analysis v Analysis of steady states in phase plane x 1 = 0 : x 1 =. . x 2 = 0 0 x 2 = 0 : x 2 = 1 1 f (x 2) 2 f (x 1) 2 x 2 v Two stable and one unstable steady state. System will converge to one of two stable steady states (differentiation) v System displays hysteresis effect: perturbation may cause irreversible switch to another steady state 15

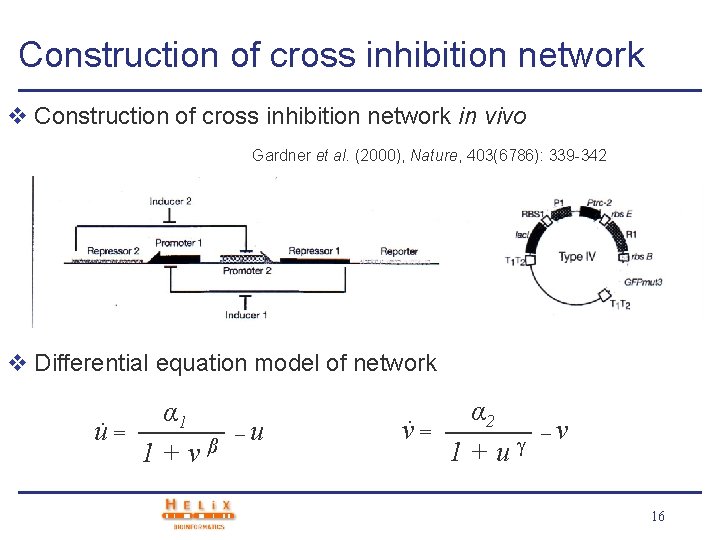
Construction of cross inhibition network v Construction of cross inhibition network in vivo Gardner et al. (2000), Nature, 403(6786): 339 -342 v Differential equation model of network. u= α 1 1+vβ –u . v= α 2 1+u –v 16

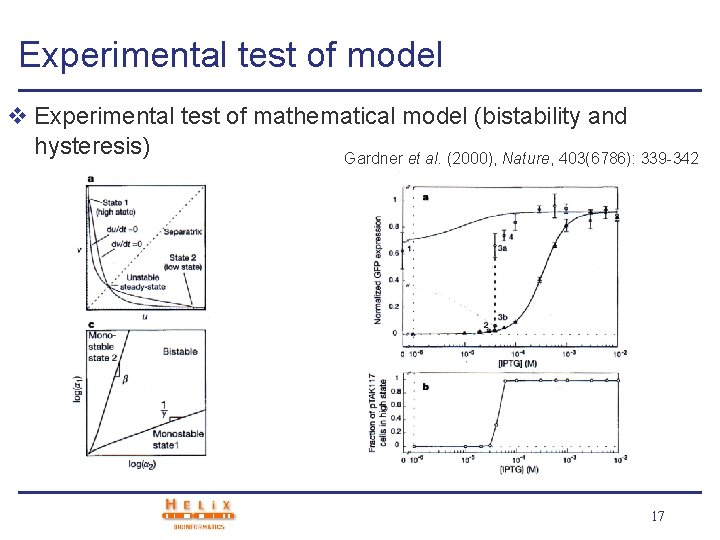
Experimental test of model v Experimental test of mathematical model (bistability and hysteresis) Gardner et al. (2000), Nature, 403(6786): 339 -342 17

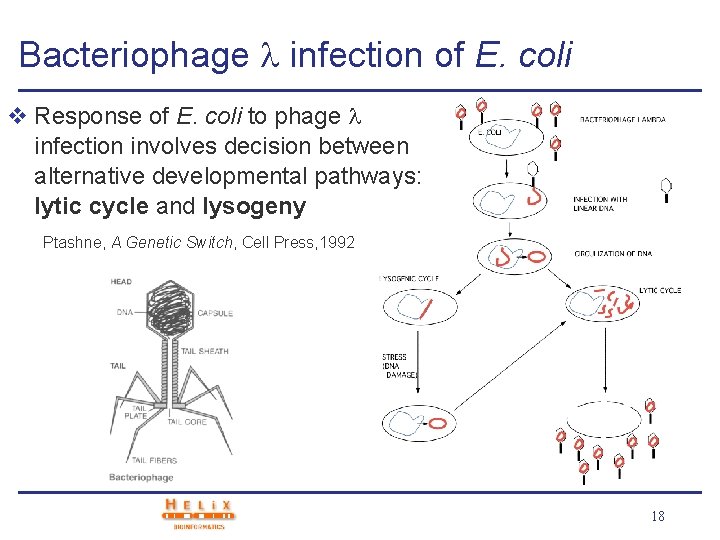
Bacteriophage infection of E. coli v Response of E. coli to phage infection involves decision between alternative developmental pathways: lytic cycle and lysogeny Ptashne, A Genetic Switch, Cell Press, 1992 18

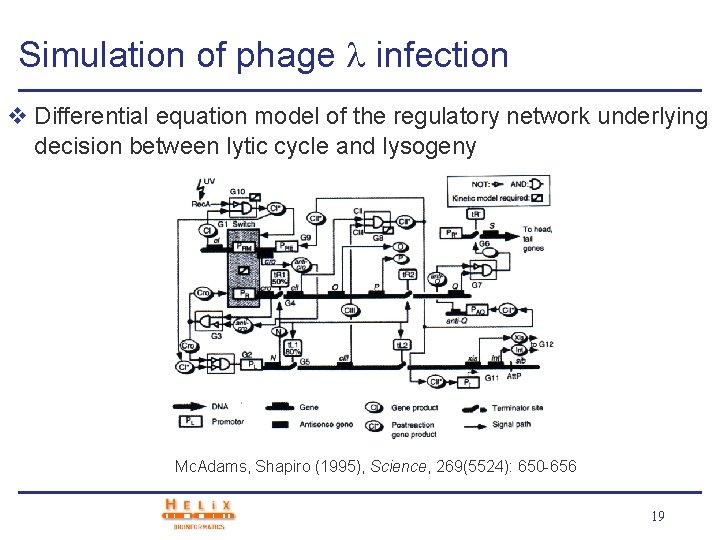
Simulation of phage infection v Differential equation model of the regulatory network underlying decision between lytic cycle and lysogeny Mc. Adams, Shapiro (1995), Science, 269(5524): 650 -656 19

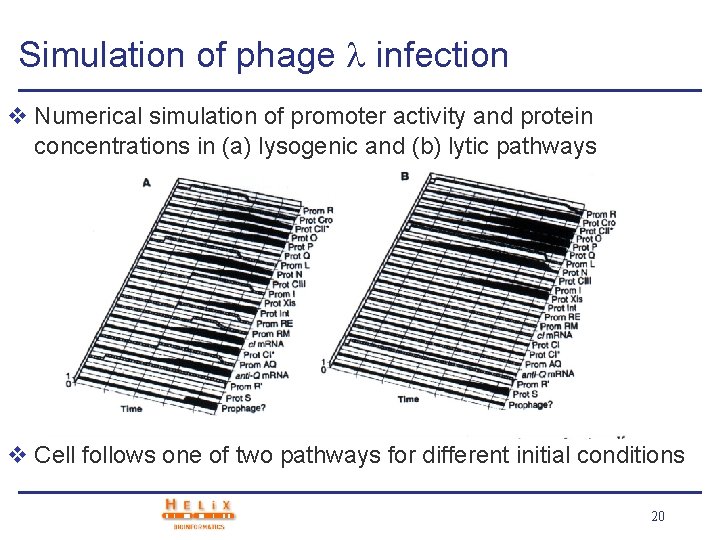
Simulation of phage infection v Numerical simulation of promoter activity and protein concentrations in (a) lysogenic and (b) lytic pathways v Cell follows one of two pathways for different initial conditions 20

Evaluation nonlinear differential equations v Pro: reasonably accurate description of underlying molecular interactions v Contra: for more complex networks, difficult to analyze mathematically, due to nonlinearities v Pro: approximate solution can be obtained through numerical simulation v Contra: simulation techniques difficult to apply in practice, due to lack of numerical values for parameters and initial conditions 21

Linear differential equation models v Cellular concentration of proteins, m. RNAs, and other molecules at time-point t represented by continuous variable xi(t) R 0 v Regulatory interactions modeled by differential equations dx. x f (x) Ax b, dt where x [x 1, …, xn]´ and f (x) is linear rate law v Analytical solution exists for linear differential equations: t x(t) e. At x 0 e. A(t-τ) dτ b 0 22

Model of cross-inhibition network gene 1 gene 2 x 1 = 1 f (x 2) 1 x 1. x 2 = 2 f (x 1) 2 x 2. 1 1, 2 > 0, production rate constants 1, 2 > 0, degradation rate constants f (x) = 1 x / (2 ) , f (x ) 0 x 1 = concentration protein 1 x 2 = concentration protein 2 2 x > 0, x 2 x 1 = 1 x 1 1 1 x 2 1. x 2 = 2 2 x 1 2 x 2 2. 23

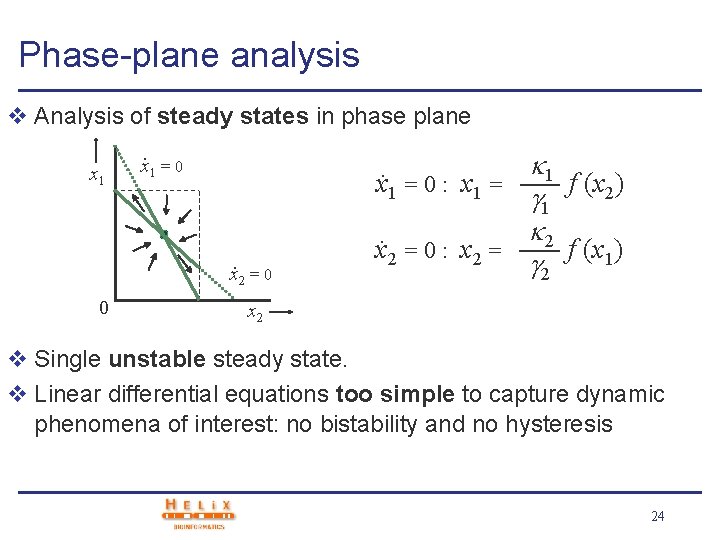
Phase-plane analysis v Analysis of steady states in phase plane x 1 = 0 : x 1 =. . x 2 = 0 0 x 2 = 0 : x 2 = 1 1 f (x 2) 2 f (x 1) 2 x 2 v Single unstable steady state. v Linear differential equations too simple to capture dynamic phenomena of interest: no bistability and no hysteresis 24

Model induction v Linear differential equation models much used for induction of model of regulatory network from gene expression data network reconstruction, reverse engineering v Given time-series of gene expression data, find A and b, such that solution of. x Ax b ξ, with noise term ξ, fits expression data v Powerful techniques for induction of linear model from experimental data Ljung (1995), System Identification, Prentice Hall, 1999 25

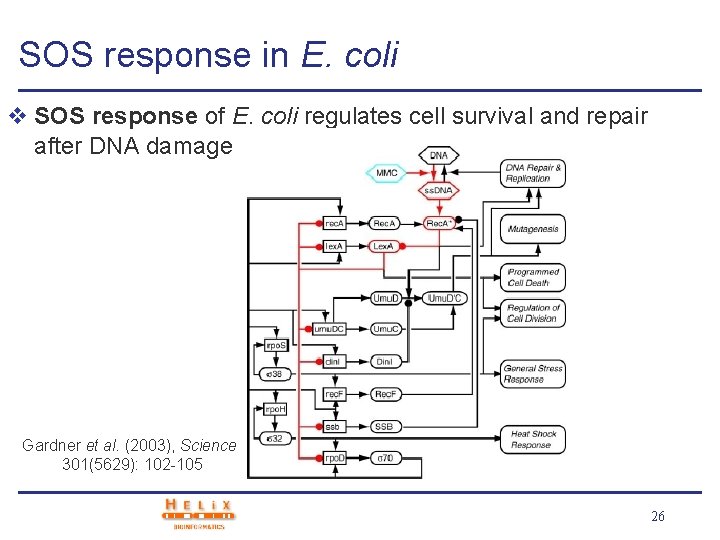
SOS response in E. coli v SOS response of E. coli regulates cell survival and repair after DNA damage Gardner et al. (2003), Science, 301(5629): 102 -105 26

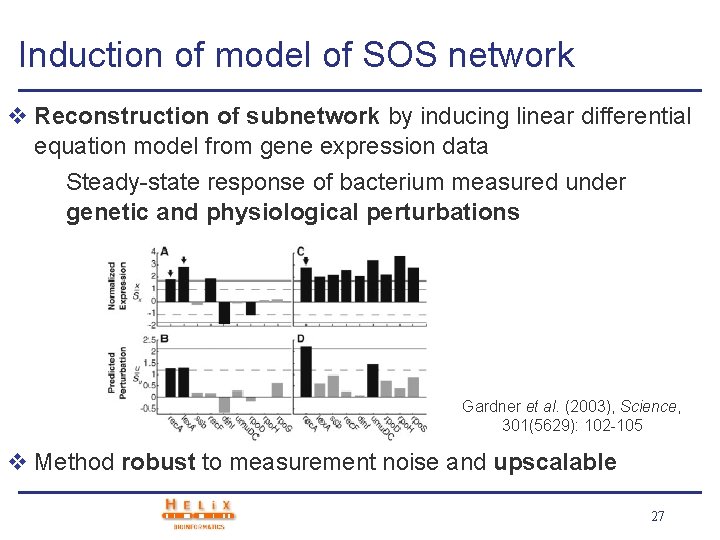
Induction of model of SOS network v Reconstruction of subnetwork by inducing linear differential equation model from gene expression data Steady-state response of bacterium measured under genetic and physiological perturbations Gardner et al. (2003), Science, 301(5629): 102 -105 v Method robust to measurement noise and upscalable 27

Evaluation of linear differential equations v Pro: analytical solution exists, thus facilitating qualitative analysis of complex systems v Contra: too simple to capture important dynamical phenomena of regulatory network, due to neglect of nonlinear character of interactions v Pro: powerful techniques for induction of model of network from gene expression data 28

Piecewise-linear differential equation models v Cellular concentration of proteins, m. RNAs, and other molecules at time-point t represented by continuous variable xi(t) R 0 v Regulatory interactions modeled by differential equations A D 1 x dx. x f (x) dt b. D 1, b. Dm, n D 1 R 0 A Dm x n Dm R 0 where x [x 1, …, xn]´and f (x) is piecewise-linear (PL) v Global solution obtained by piecing together local solutions of linear differential equations in regions Dj 29

Model of cross-inhibition network gene 1 gene 2 x. 1 = 1 f (x 2) 1 x. 2 = 2 f (x 1) 2 x 1 = concentration protein 1 x 2 = concentration protein 2 1, 2 > 0, production rate constants 1, 2 > 0, degradation rate constants f (x ) 1 0 f (x) = s ( x, ) = 1, x < 0, x > x 30

Phase-plane analysis v Analysis of dynamics in phase plane x 1 x. 1 = 1 s (x 2, 2) 1 x 1. x 2 = 2 s (x 1, 1) 2 x 2 . x 1 = 0. 1 x 2 = 0 D 1 D 2 0 x. 1 = 0 2 . x 2 = 0 x 2 in D 21 : x 1 = 1 1 x 1 , x 1 = 0 : x 1 =c = 01 1. . , x x 2 = 2 2 x 2 2 = 0 : x 2 = 2 2. . v In every region Dj , model simplifies to system of piecewiseaffine differential equations All solutions, while being in Dj , converge towards target steady state v Different regions have different target steady states 31

Phase-plane analysis v Global phase-plane analysis by combining analyses in local regions of phase plane Techniques for dealing with discontinuities due to step functions x 1 Gouzé, Sari (2003), Dyn. Syst. , 17(4): 299 -316 . x 1 = 0 1. x 2 = 0 0 2 x 2 v Piecewise-linear model good approximation of nonlinear model, retaining properties of bistability and hysteresis 32

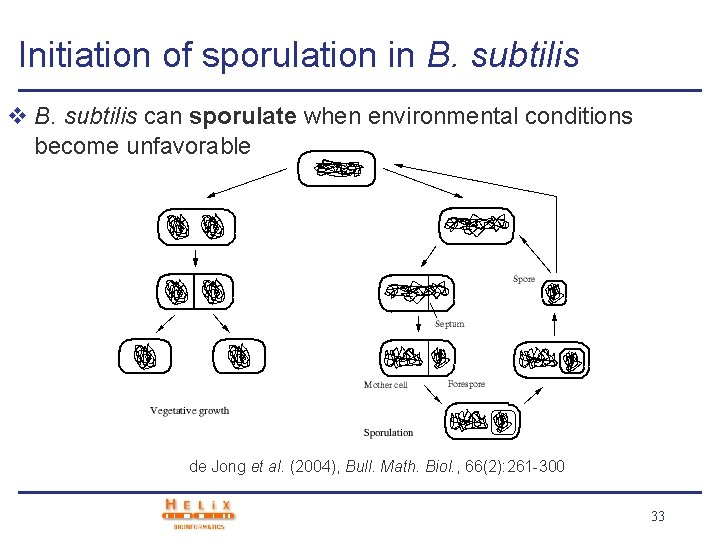
Initiation of sporulation in B. subtilis v B. subtilis can sporulate when environmental conditions become unfavorable de Jong et al. (2004), Bull. Math. Biol. , 66(2): 261 -300 33

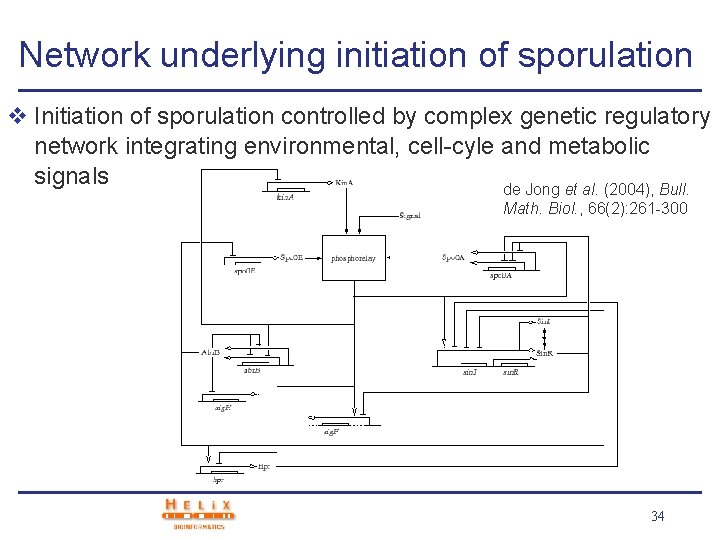
Network underlying initiation of sporulation v Initiation of sporulation controlled by complex genetic regulatory network integrating environmental, cell-cyle and metabolic signals de Jong et al. (2004), Bull. Math. Biol. , 66(2): 261 -300 34

Genetic Network Analyzer (GNA) v Qualitative simulation of initiation of sporulation using tool based on piecewise-linear differential equation models (GNA) de Jong et al. (2003), Bioinformatics, 19(3): 336 -344 35

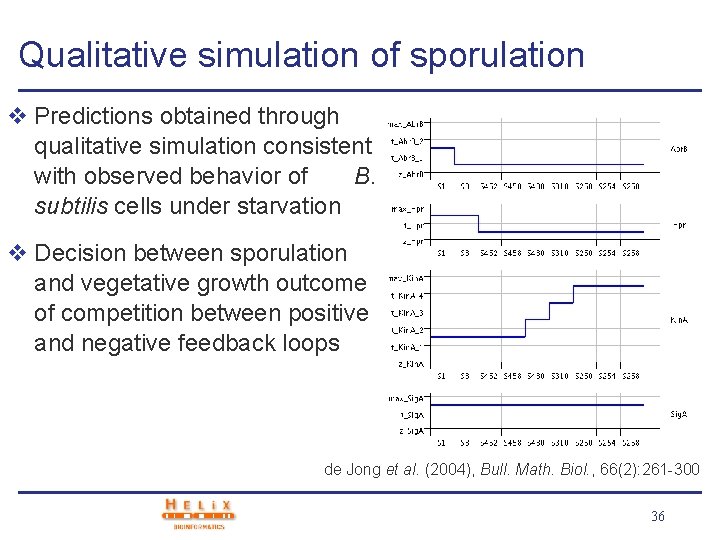
Qualitative simulation of sporulation v Predictions obtained through qualitative simulation consistent with observed behavior of B. subtilis cells under starvation v Decision between sporulation and vegetative growth outcome of competition between positive and negative feedback loops de Jong et al. (2004), Bull. Math. Biol. , 66(2): 261 -300 36

Evaluation of PL differential equations v Pro: captures important dynamical phenomena of network, by suitable approximation of nonlinearities v Pro: qualitative analysis of dynamics of complex systems possible, due to favorable mathematical properties v Pro: powerful techniques for induction of model of network from gene expression data 37

Conclusions v Several kinds of mathematical model of genetic regulatory networks v Nonlinear models give reasonably accurate description of regulatory interactions, but difficult to apply in practice v Linear models have favorable mathematical and computational properties, but can only give rough picture of regulatory structure v Piecewise-linear models are compromise between nonlinear and linear models, satisfying biological applicability and computational feasibility 38

Beyond modeling and simulation v Integration of modeling and simulation with other computational and experimental tools: l Biological knowledge and databases l Selection of discriminatory experiments l Validation of model predictions with experimental data biological system experimental conditions choose experiments experimental simulate conditions observations predictions compare perform experiments models biological knowledge construct and revise models fit of models observations 39

Beyond genetic regulatory networks v Integration of genetic networks with metabolic and signal transduction networks Virtual cell or whole-cell simulation Tomita et al. (1999), Bioinformatics, 15(1): 72 -84 40