PARTIAL DIFFERENTIAL EQUATIONS Formation of Partial Differential equations





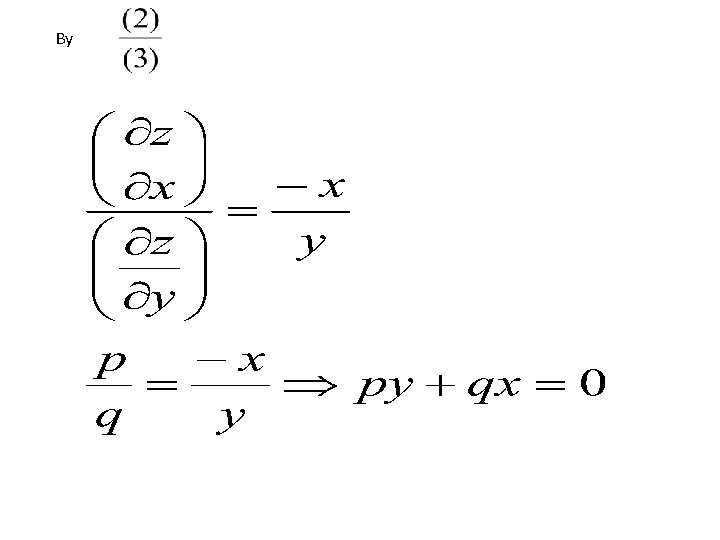

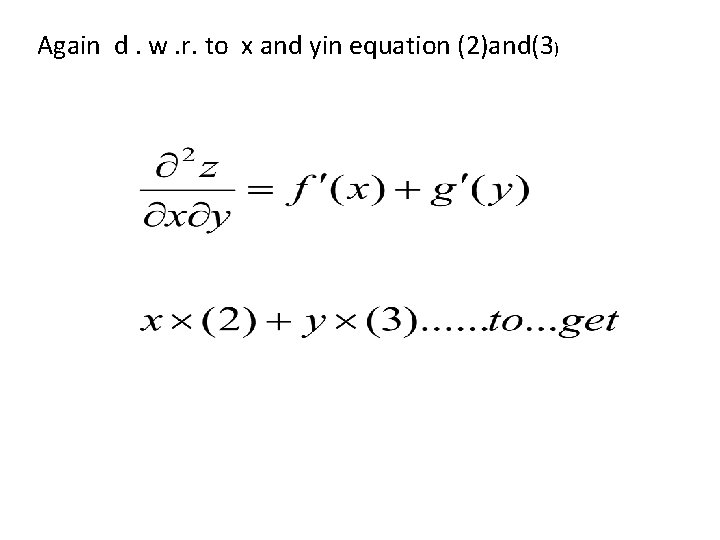





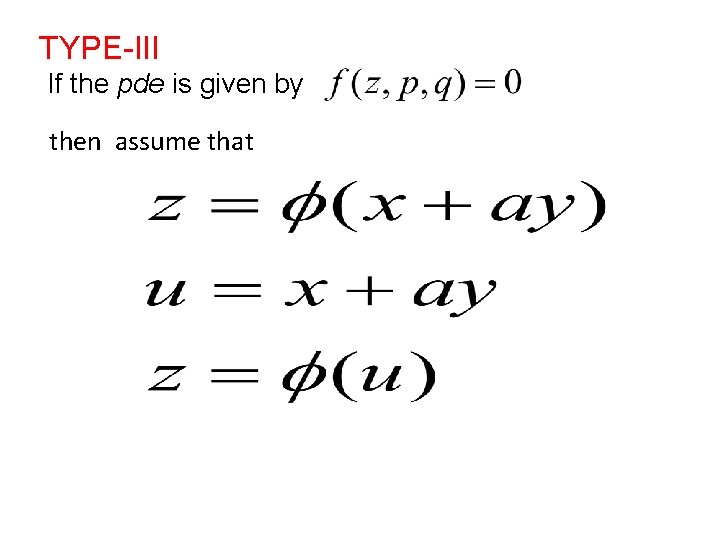








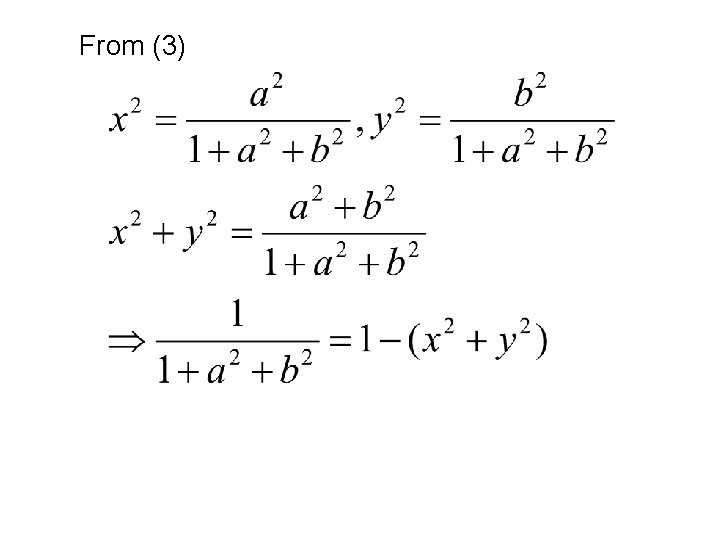


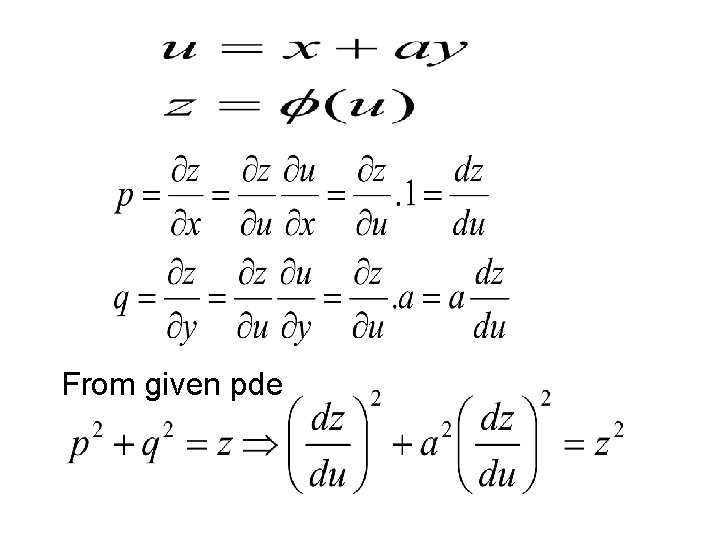






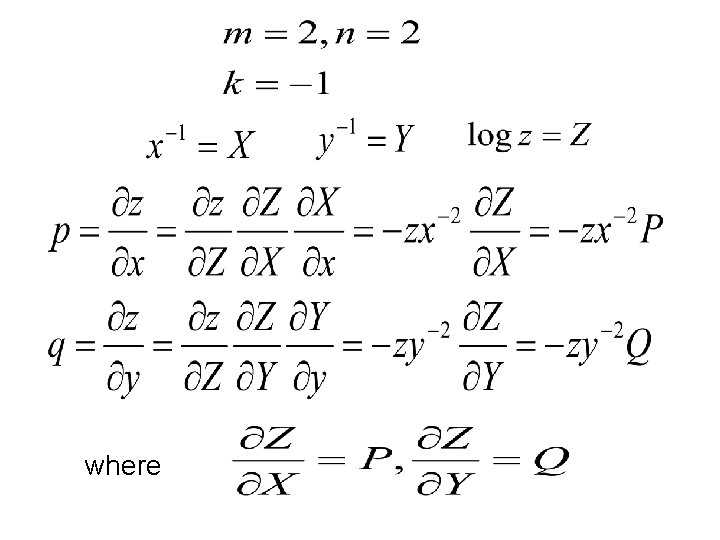
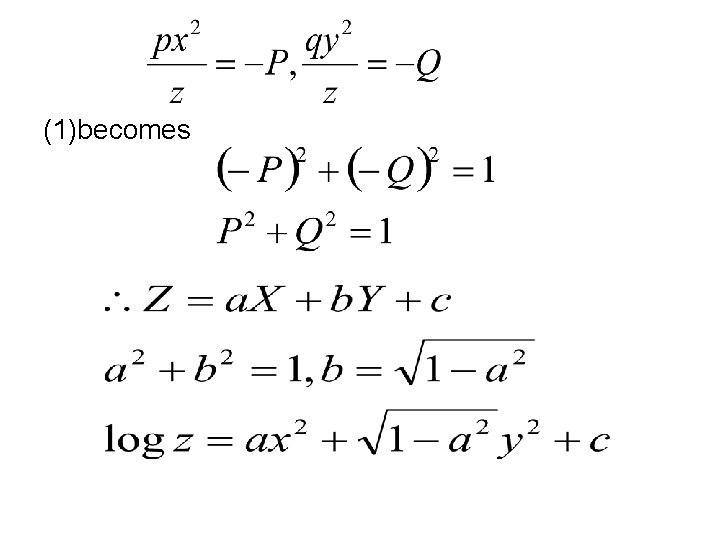

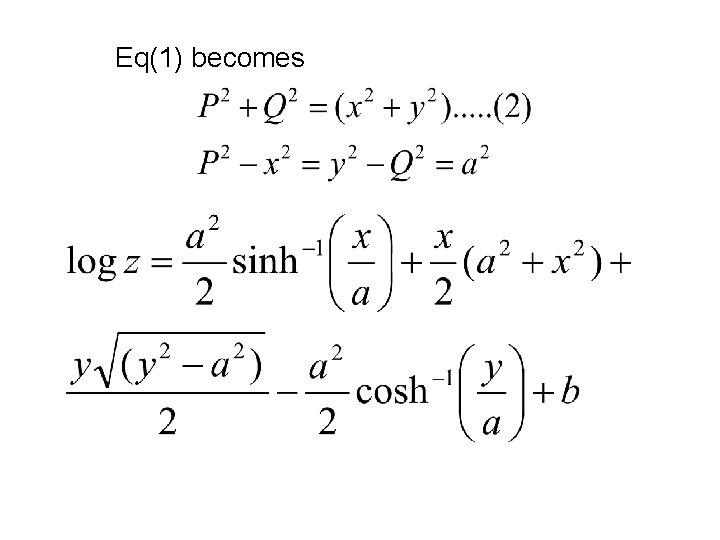



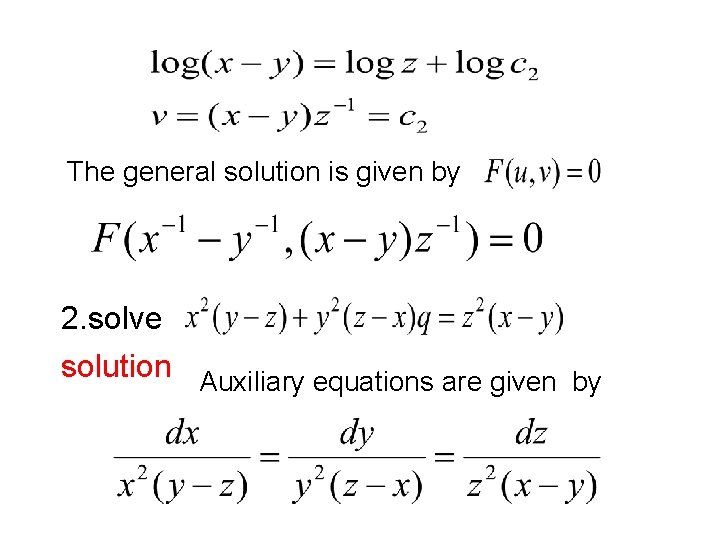

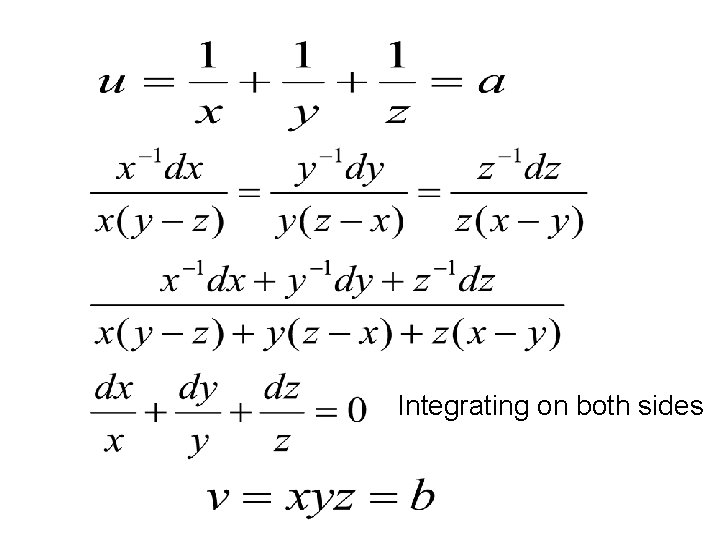





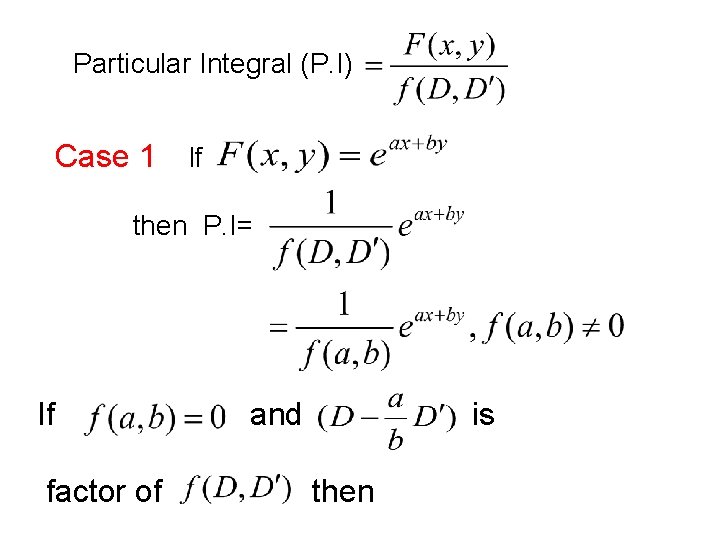
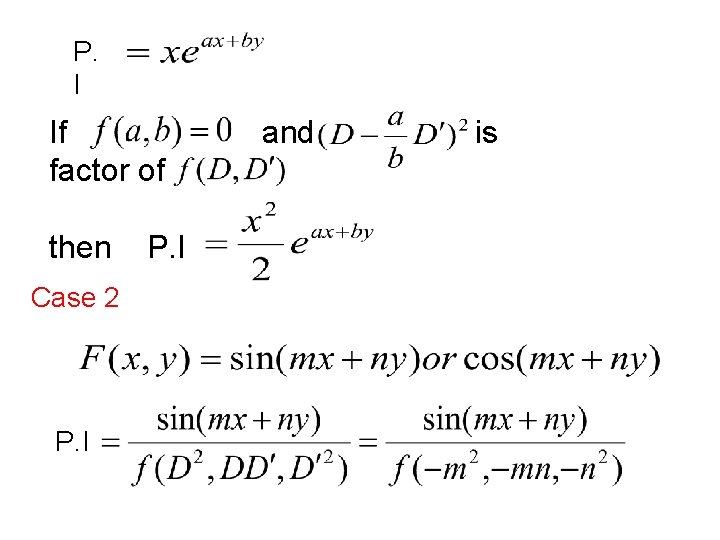



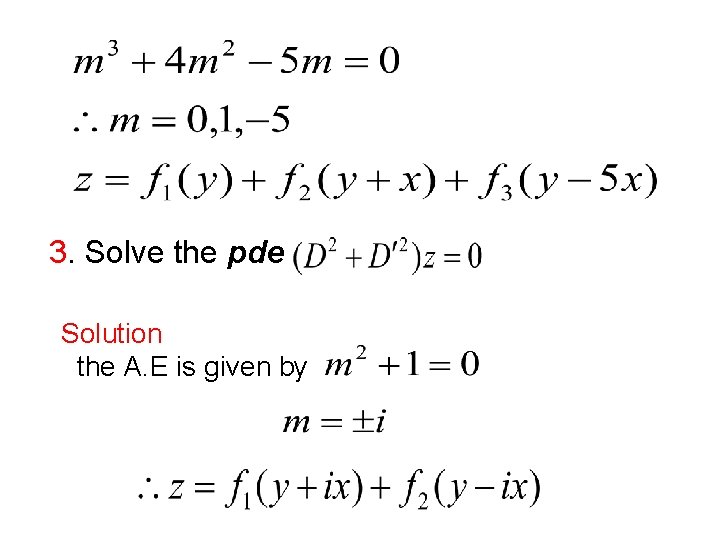


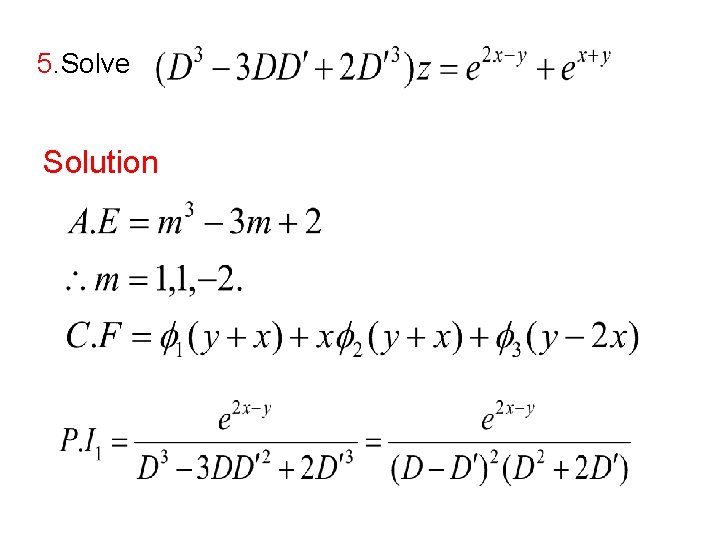
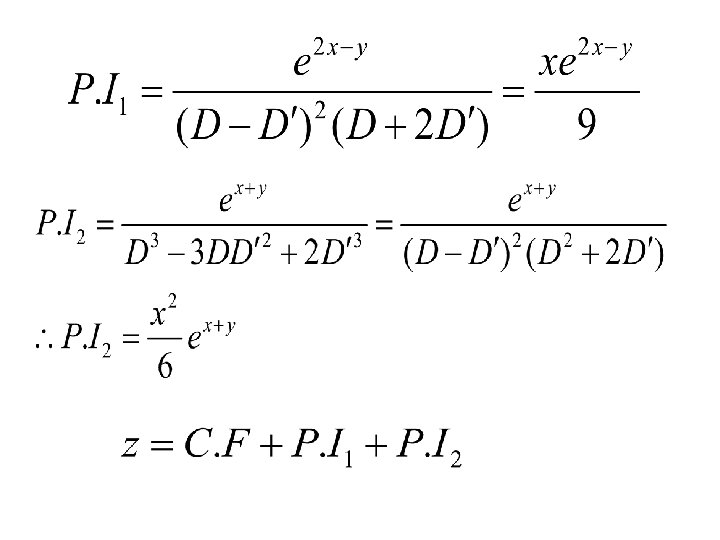
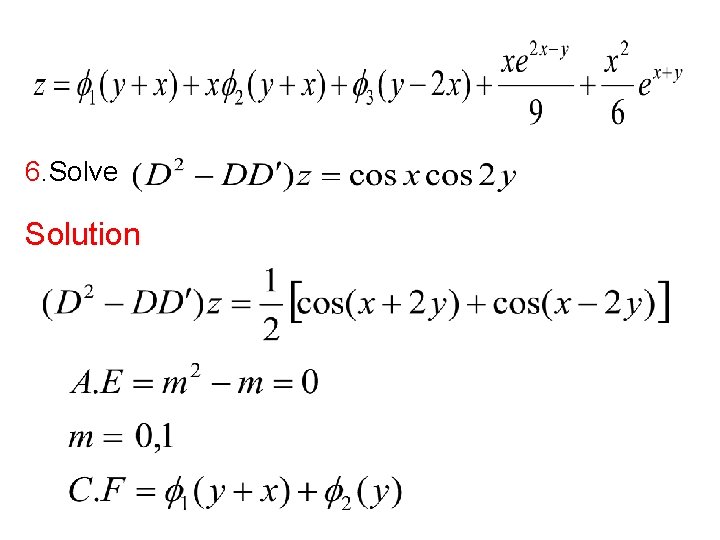
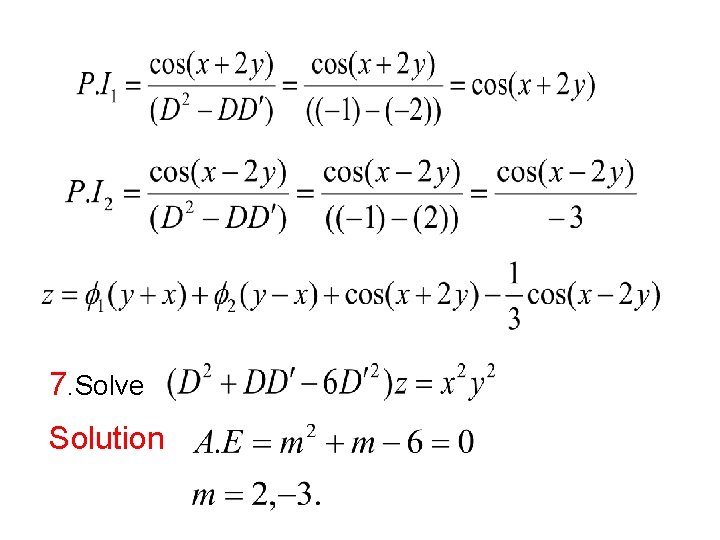
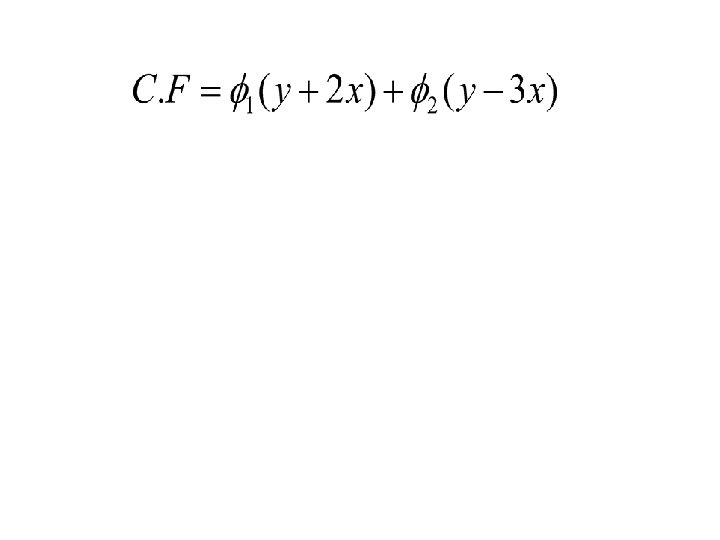


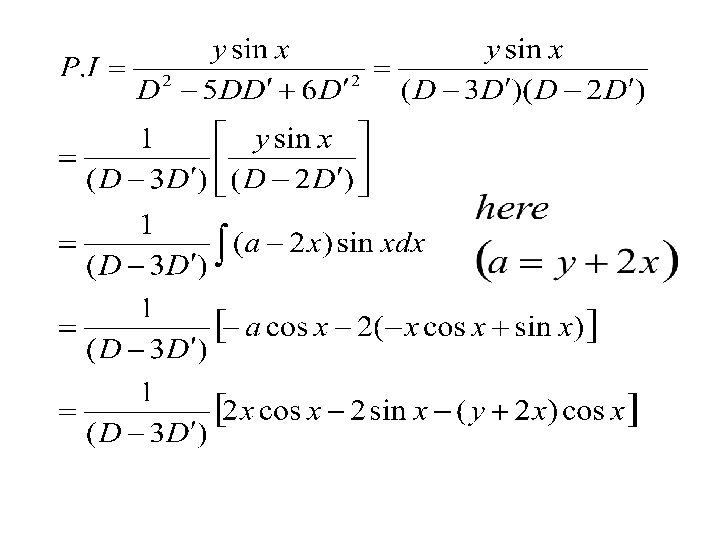
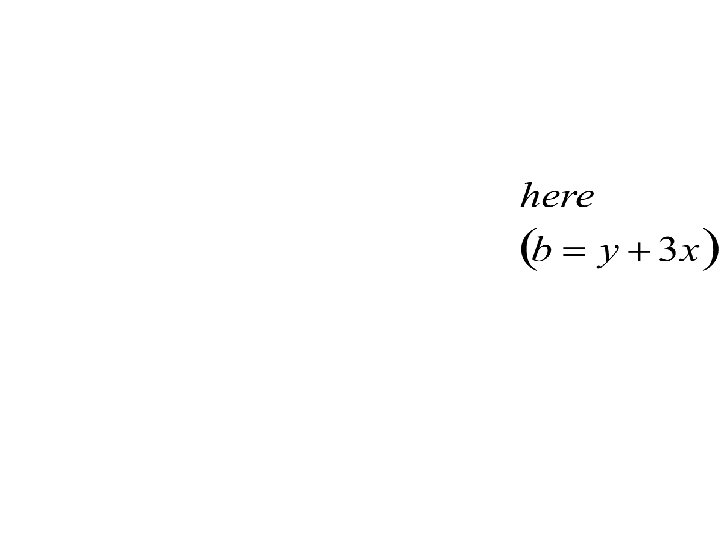



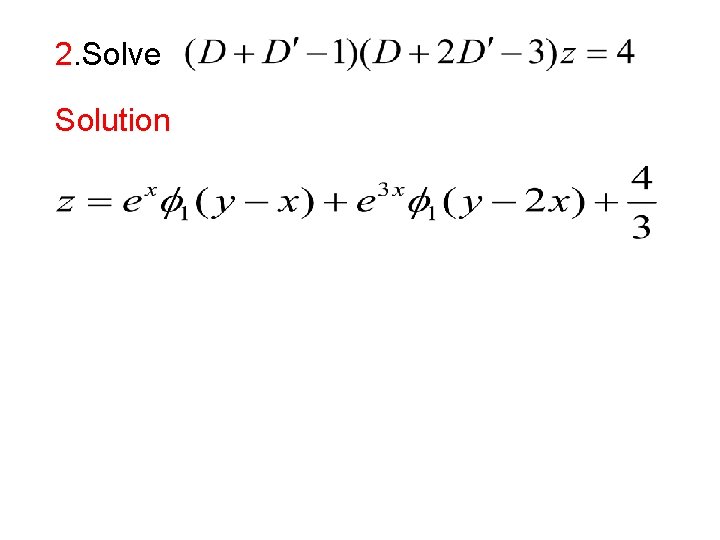
- Slides: 72

PARTIAL DIFFERENTIAL EQUATIONS

Formation of Partial Differential equations Partial Differential Equation can be formed either by elimination of arbitrary constants or by the elimination of arbitrary functions from a relation involving three or more variables. SOLVED PROBLEMS 1. Eliminate two arbitrary constants a and b from here R is known constant.

(OR) Find the differential equation of all spheres of fixed radius having their centers in x y- plane. solution Differentiating both sides with respect to x and y

By substituting all these values in (1) or

2. Find the partial Differential Equation by eliminating arbitrary functions from SOLUTION
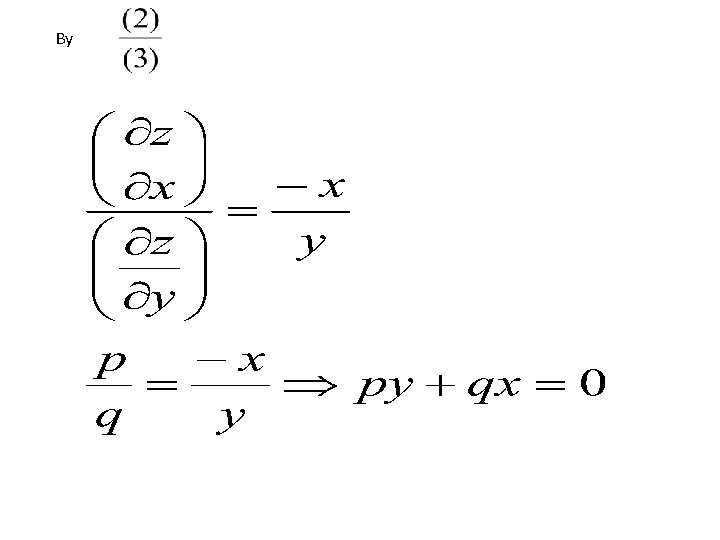
By

3. Find Partial Differential Equation by eliminating two arbitrary functions from SOLUTION Differentiating both sides with respect to x and y
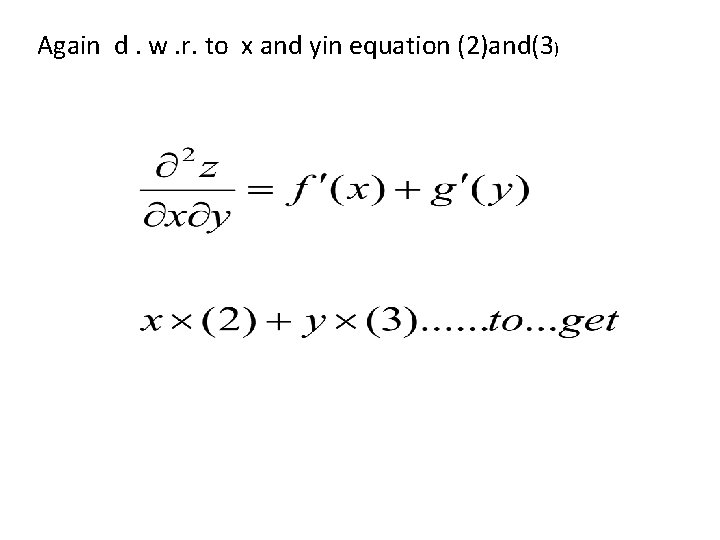
Again d. w. r. to x and yin equation (2)and(3)


Different Integrals of Partial Differential Equation 1. Complete Integral (solution) Let be the Partial Differential Equation. The complete integral of equation (1) is given by

2. Particular solution A solution obtained by giving particular values to the arbitrary constants in a complete integral is called particular solution. 3. Singular solution The eliminant of a , b between when it exists , is called singular solution

4. General solution In equation (2) assume an arbitrary relation of the form. Then (2) becomes Differentiating (2) with respect to a, The eliminant of (3) and (4) if exists, is called general solution

Standard types of first order equations TYPE-I The Partial Differential equation of the form has solution with TYPE-II The Partial Differential Equation of the form is called Clairaut’s form of pde , it’s solution is given by
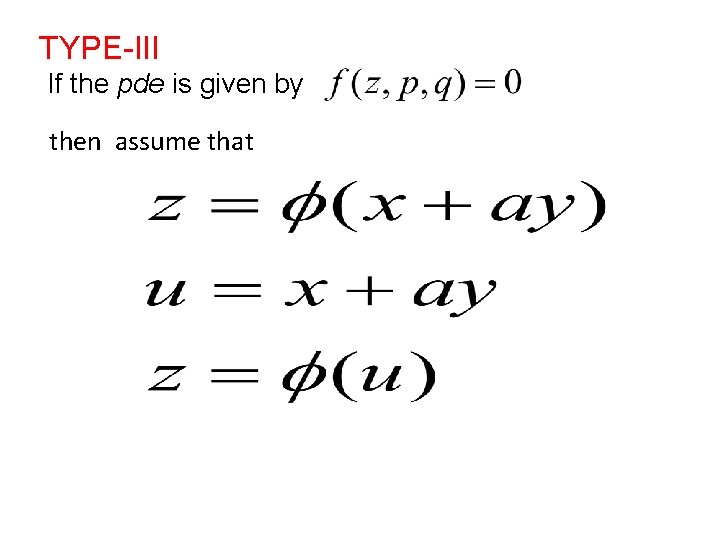
TYPE-III If the pde is given by then assume that

The given pde can be written as. And also this can be integrated to get solution

TYPE-IV The pde of the form solved by assuming can be Integrate the above equation to get solution

SOLVED PROBLEMS 1. Solve the pde and singular solutions and find the complete Solution Complete solution is given by with

d. w. r. to. a and c then Which is not possible Hence there is no singular solution 2. Solve the pde and find the complete, general and singular solutions

Solution The complete solution is given by with

no singular solution To get general solution assume that From eq (1)

Eliminate from (2) and (3) to get general solution 3. Solve the pde and find the complete and singular solutions Solution The pde is in Clairaut’s form

complete solution of (1) is d. w. r. to “a” and “b”
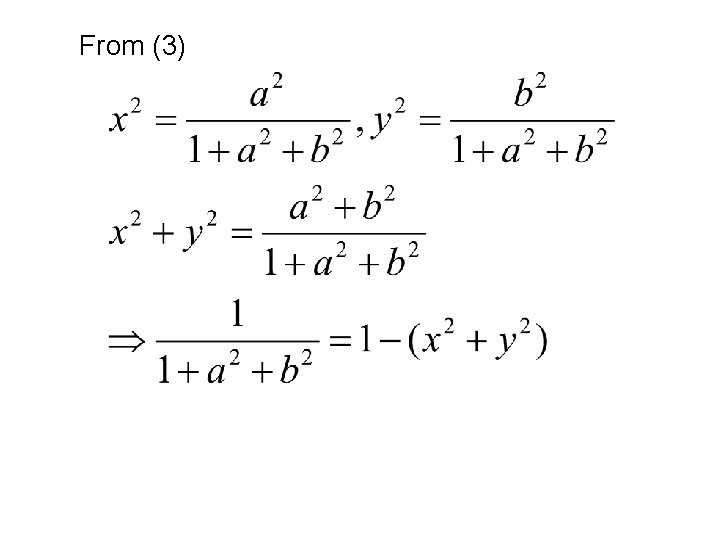
From (3)

is required singular solution

4. Solve the pde Solution pde Complete solution of above pde is 5. Solve the pde Solution Assume that
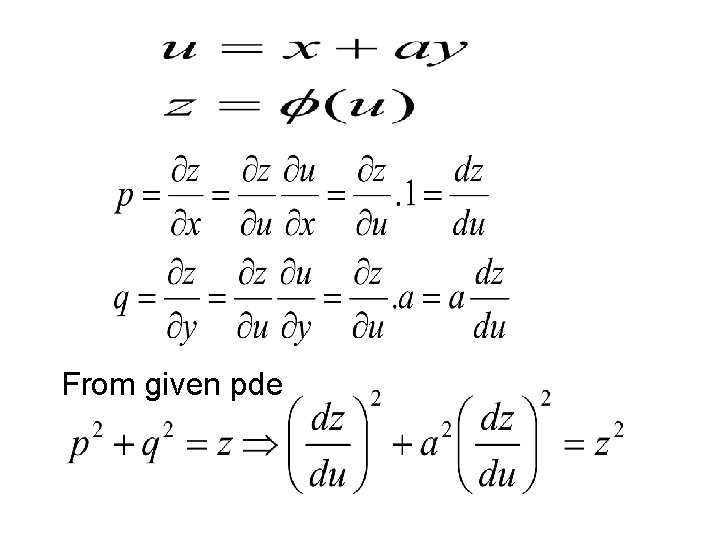
From given pde
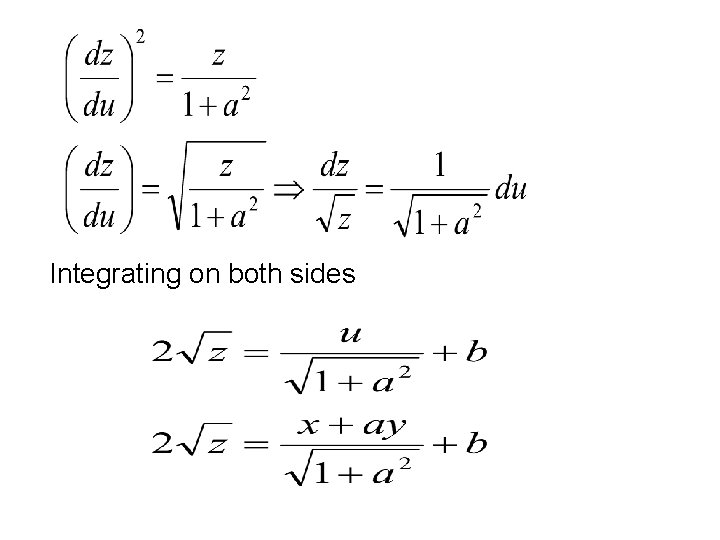
Integrating on both sides

6. Solve the pde Solution Assume Substituting in given equation

Integrating on both sides 7. Solve pde (or) Solution

Assume that Integrating on both sides

8. Solve the equation Solution integrating

Equations reducible to the standard forms (i)If and occur in the pde as in Or in Case (a) Put if and ;
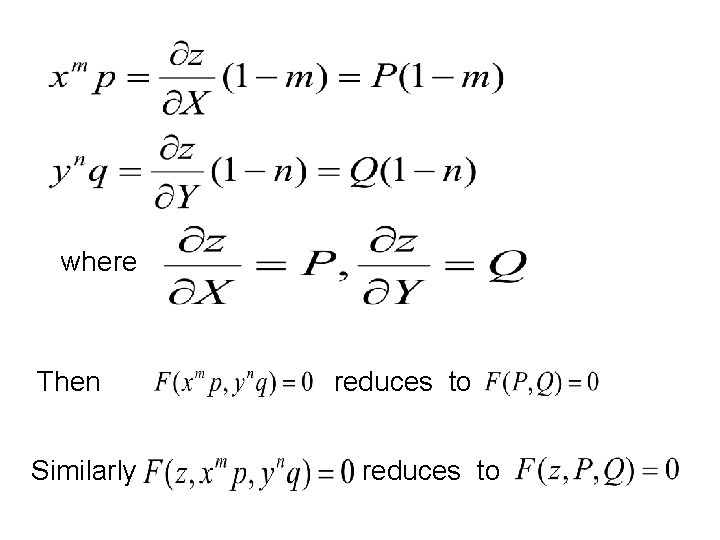
where Then Similarly reduces to
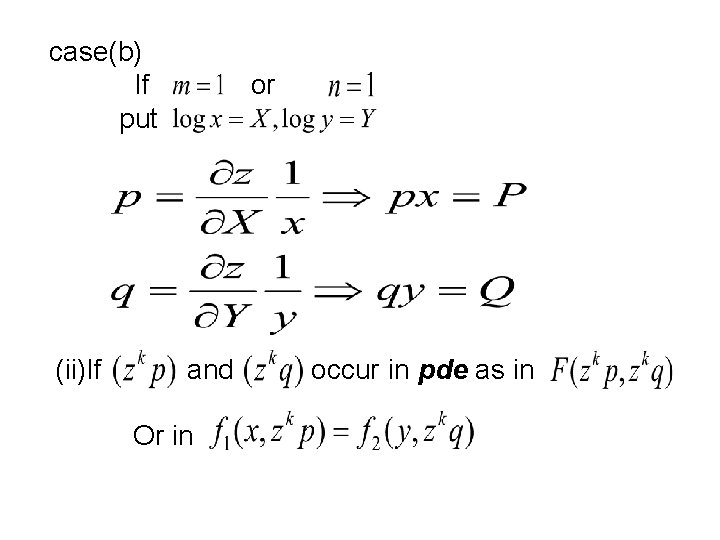
case(b) If put (ii)If or and Or in occur in pde as in
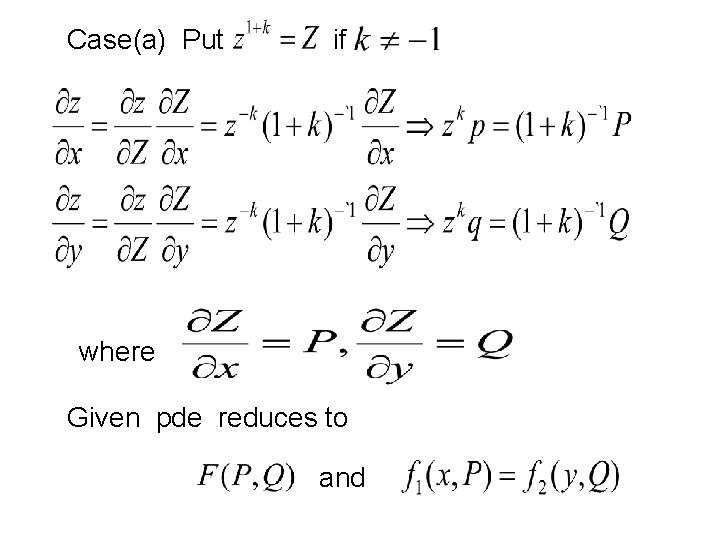
Case(a) Put if where Given pde reduces to and

Case(b) if Solved Problems 1. Solve Solution
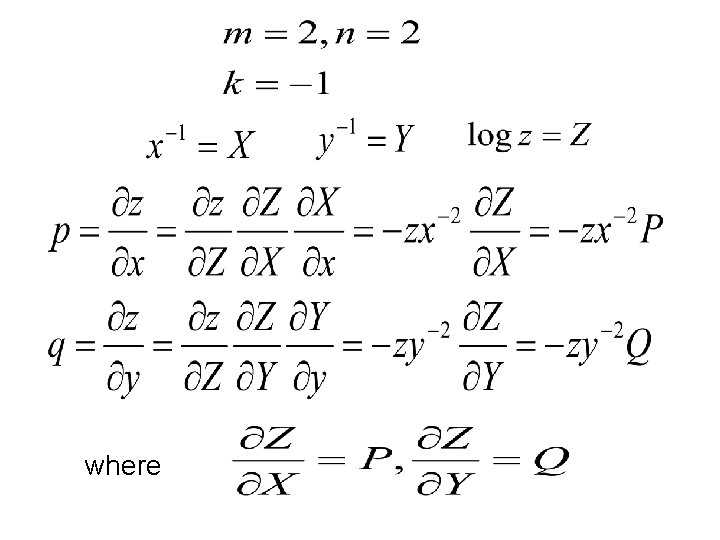
where
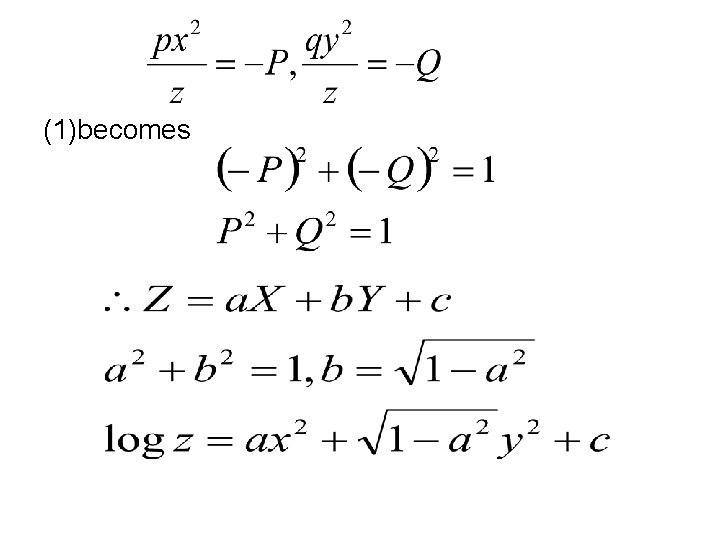
(1)becomes

2. Solve the pde SOLUTION
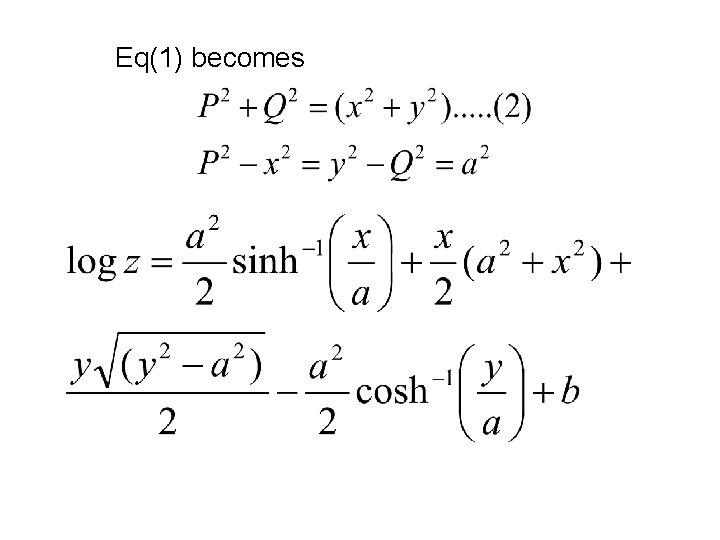
Eq(1) becomes

Lagrange’s Linear Equation Def: The linear partial differenfial equation of first order is called as Lagrange’s linear Equation. This eq is of the form Where and are functions x, y and z The general solution of the partial differential equation is Where and is arbitrary function of

Here and are independent solutions of the auxilary equations Solved problems 1. Find the general solution of Solution auxilary equations are

Integrating on both sides
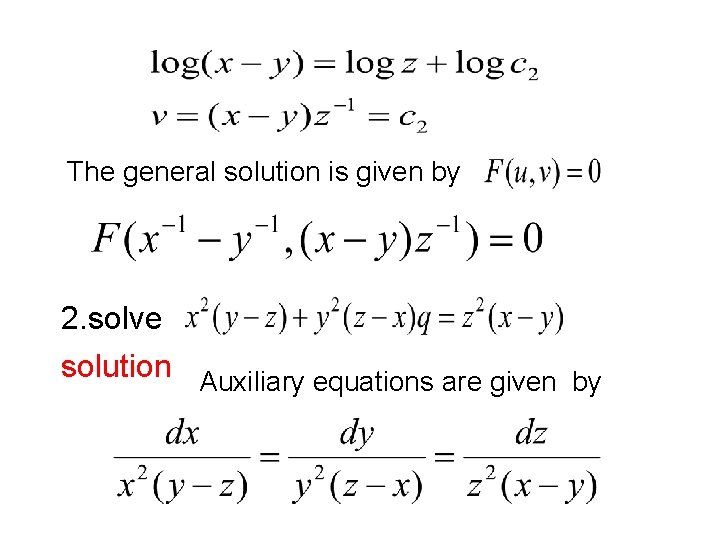
The general solution is given by 2. solve solution Auxiliary equations are given by

Integrating on both sides
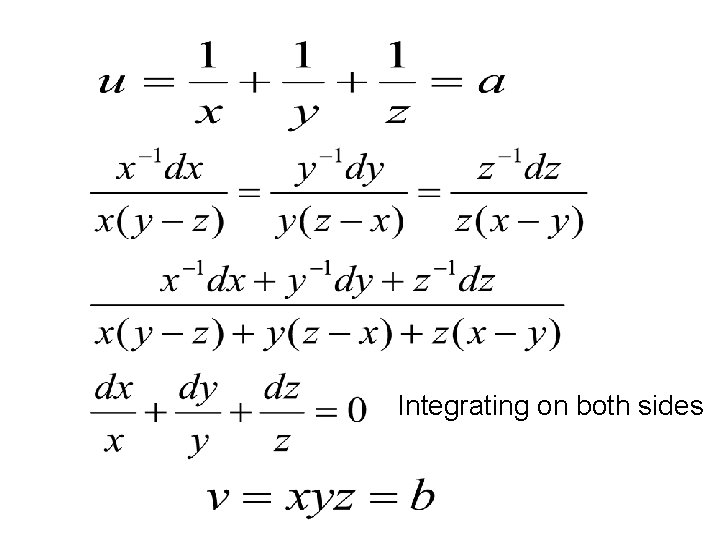
Integrating on both sides

The general solution is given by HOMOGENEOUS LINEAR PDE WITH CONSTANT COEFFICIENTS Equations in which partial derivatives occurring are all of same order (with degree one ) and the coefficients are constants , such equations are called homogeneous linear PDE with constant coefficient

Assume that then order linear homogeneous equation is given by or

The complete solution of equation (1) consists of two parts , the complementary function and particular integral. The complementary function is complete solution of equation of Rules to find complementary function Consider the equation or

The auxiliary equation for (A. E) is given by And by giving The A. E becomes Case 1 If the equation(3) has two distinct roots The complete solution of (2) is given by

Case 2 If the equation(3) has two equal roots i. e The complete solution of (2) is given by Rules to find the particular Integral Consider the equation
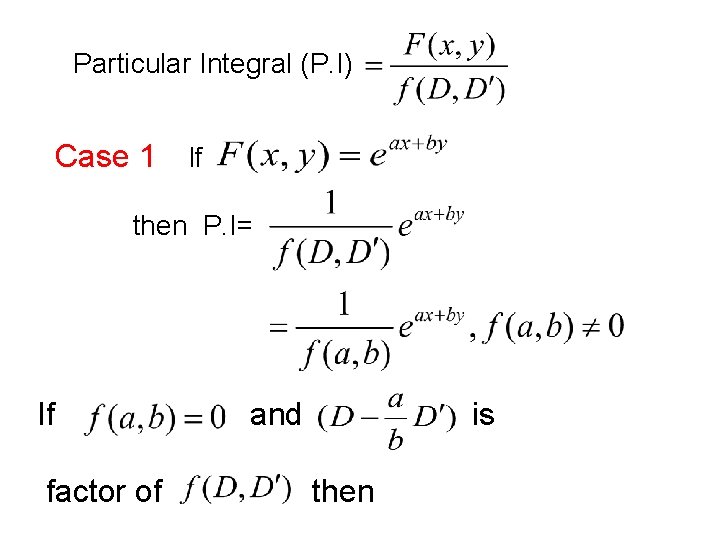
Particular Integral (P. I) Case 1 If then P. I= If factor of and is then
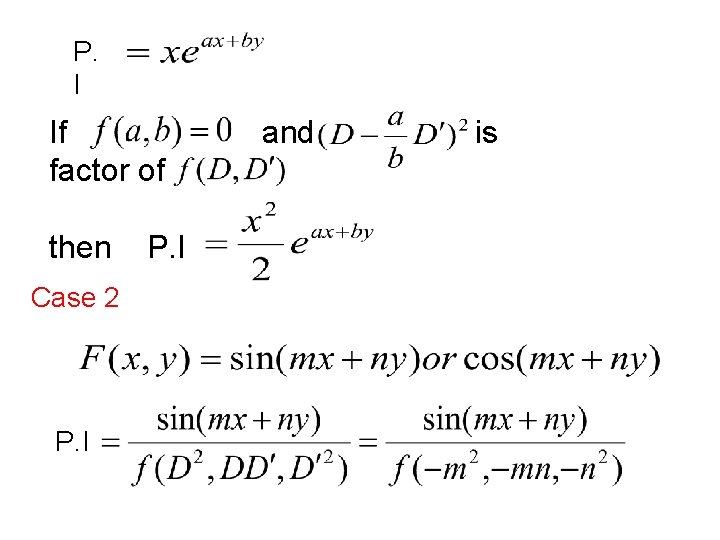
P. I If factor of then Case 2 P. I and is

Case 3 P. I Expand in ascending powers of or and operating on term by term. Case 4 when and y. P. I= is any function of x

Here is factor of Where ‘c’ is replaced by after integration Solved problems 1. Find the solution of pde Solution The Auxiliary equation is given by

Solution The Auxiliary equation is given by By taking Complete solution 2. Solve the pde Solution The Auxiliary equation is given by
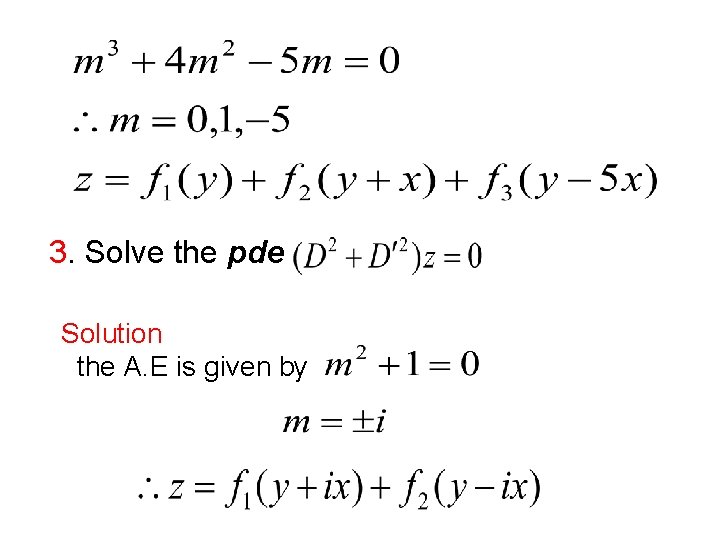
3. Solve the pde Solution the A. E is given by

4. Find the solution of pde Solution Complete solution = Complementary Function + Particular Integral The A. E is given by

Complete solution
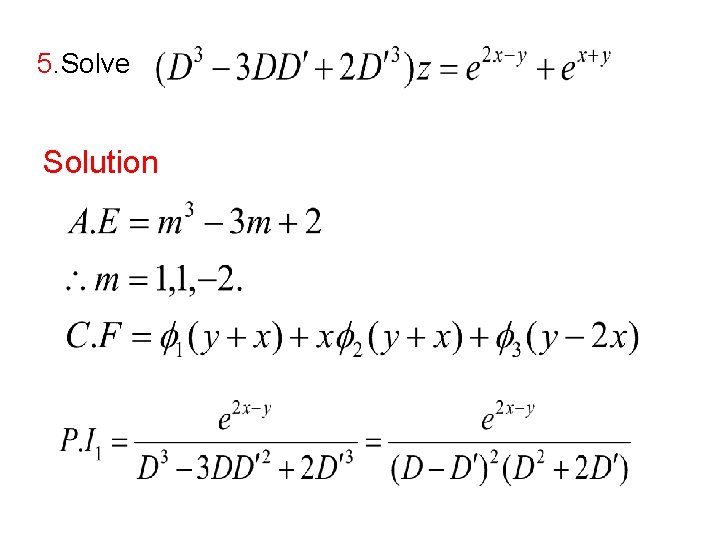
5. Solve Solution
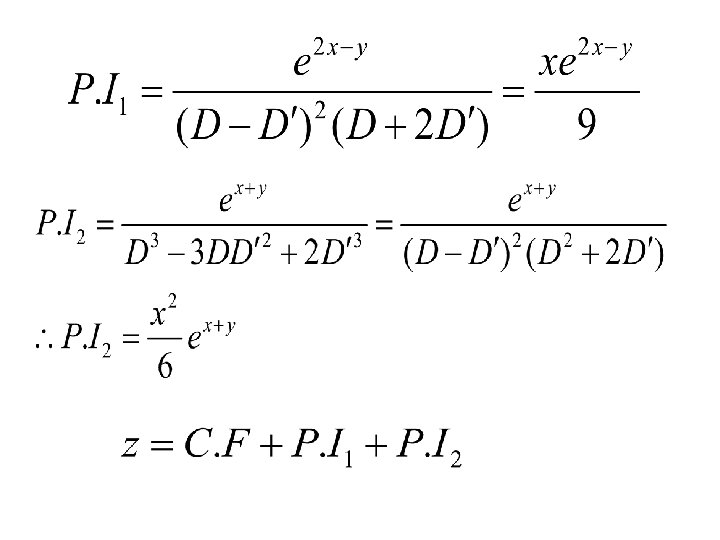
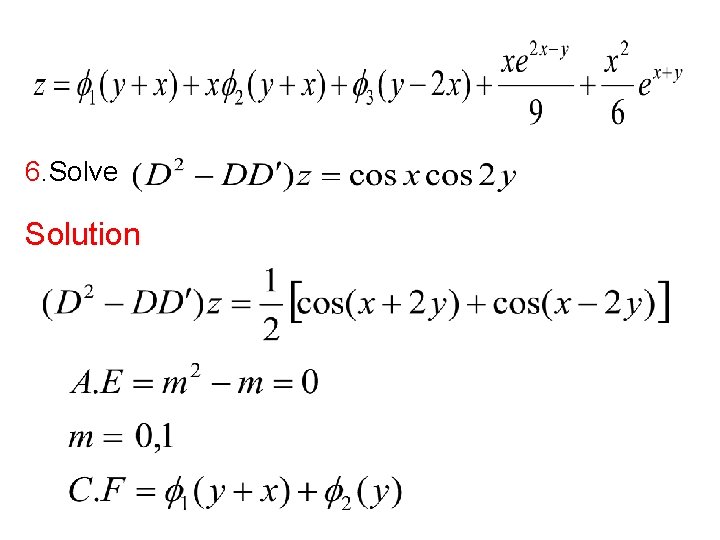
6. Solve Solution
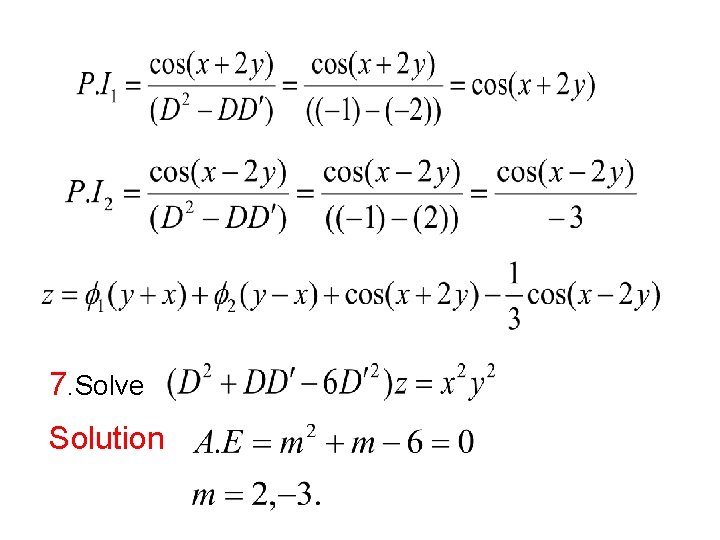
7. Solve Solution
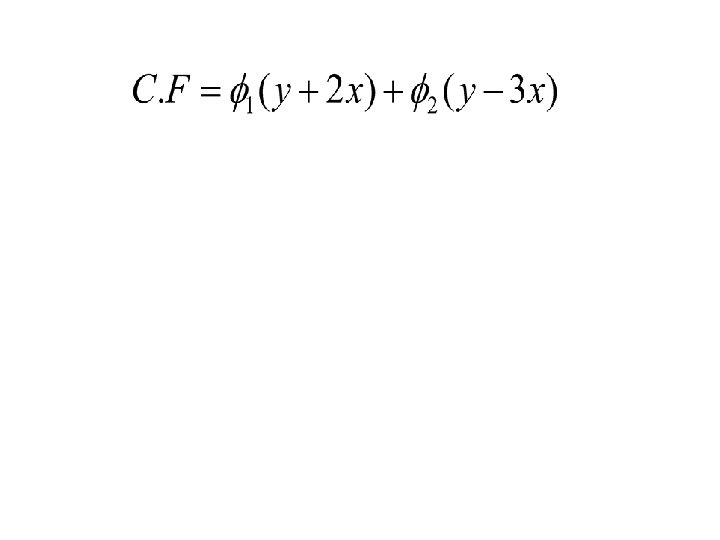


7. Solve Solution A. E is
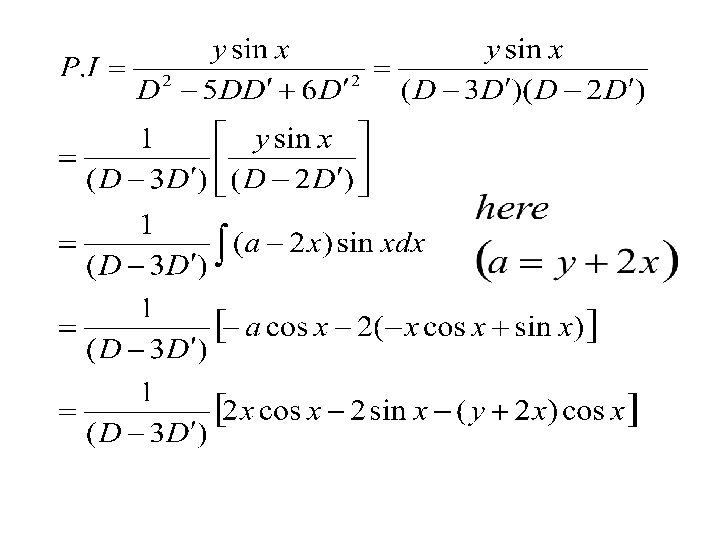
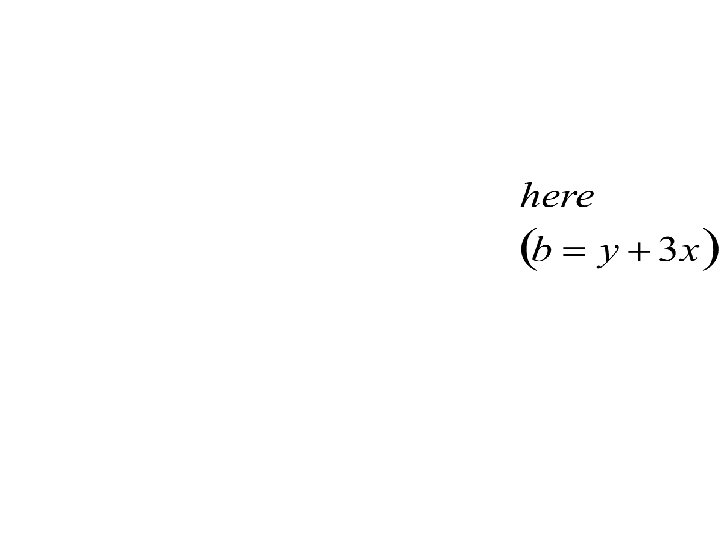

Non Homogeneous Linear PDES If in the equation the polynomial expression is not homogeneous, then (1) is a non- homogeneous linear partial differential equation Ex Complete Solution = Complementary Function + Particular Integral To find C. F. , factorize into factors of the form

If the non homogeneous equation is of the form 1. Solve Solution

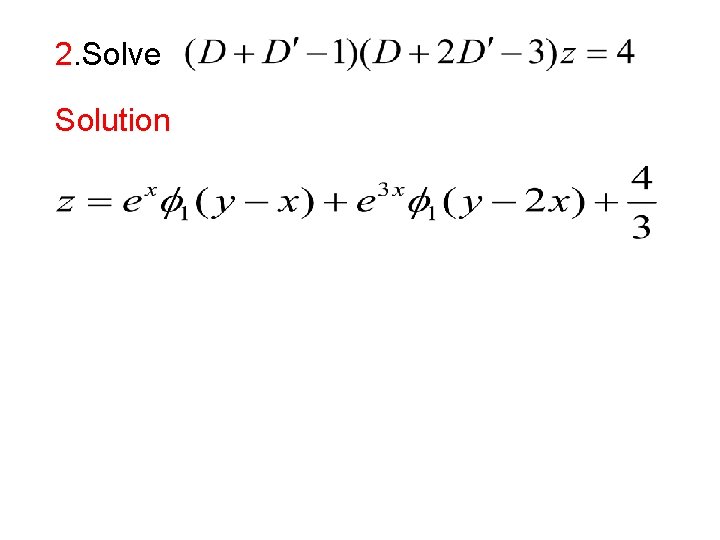
2. Solve Solution
 Bernoulli differential equation ppt
Bernoulli differential equation ppt Methods of characteristics
Methods of characteristics Partial differential equations example
Partial differential equations example Integration of partial differential equation
Integration of partial differential equation Differential formula
Differential formula Order of partial differential equation
Order of partial differential equation Numerical methods for partial differential equations eth
Numerical methods for partial differential equations eth First order linear differential equation
First order linear differential equation Formation initiale vs formation continue
Formation initiale vs formation continue Relion e01
Relion e01 General solution of partial differential equation
General solution of partial differential equation Finite difference equation
Finite difference equation Classification of pde
Classification of pde The solution of partial differential equation
The solution of partial differential equation Differential equations projects
Differential equations projects Classification of pde examples
Classification of pde examples Cengage differential equations
Cengage differential equations First order ordinary differential equations
First order ordinary differential equations Euler midpoint method
Euler midpoint method Differential equations calculus
Differential equations calculus Separation of variables differential equations
Separation of variables differential equations What is a first order equation
What is a first order equation Integrating factor of differential equation
Integrating factor of differential equation Cengage differential equations
Cengage differential equations Natural solution
Natural solution How to solve second order differential equations
How to solve second order differential equations Pde first order
Pde first order Definition and classification of differential equations
Definition and classification of differential equations Traffic flow differential equations
Traffic flow differential equations Midpoint method formula
Midpoint method formula Euler's method
Euler's method First order differential equation
First order differential equation Slidetodoc.com
Slidetodoc.com Differential equations
Differential equations Differential equations with discontinuous forcing functions
Differential equations with discontinuous forcing functions Bernoulli differential equation example
Bernoulli differential equation example Parachute problem differential equations
Parachute problem differential equations Homogeneous differential equation definition
Homogeneous differential equation definition Munthe sizing
Munthe sizing Growth and decay differential equation
Growth and decay differential equation Dennis g zill differential equations solutions
Dennis g zill differential equations solutions Stewart differential equations
Stewart differential equations Highest order chapter 1
Highest order chapter 1 Maxwell's equations differential form
Maxwell's equations differential form Mechanical and electrical vibrations differential equations
Mechanical and electrical vibrations differential equations Method of annihilators
Method of annihilators Ordinary differential equations example
Ordinary differential equations example Nonlinear ode
Nonlinear ode Higher order linear differential equations
Higher order linear differential equations Definition of differential equation
Definition of differential equation Mixing problems differential equations
Mixing problems differential equations Derivation of maxwell's equations in differential form
Derivation of maxwell's equations in differential form Differential equations with discontinuous forcing functions
Differential equations with discontinuous forcing functions Derivation of maxwell's equations in differential form
Derivation of maxwell's equations in differential form Differential equations summary
Differential equations summary Ordinary differential equations examples
Ordinary differential equations examples Logistic vs exponential growth
Logistic vs exponential growth Differential equations formulas
Differential equations formulas Hcc differential equations
Hcc differential equations Polar and rectangular forms of equations
Polar and rectangular forms of equations Translating chemical equations
Translating chemical equations Habit formation
Habit formation Illusion word formation
Illusion word formation Category extension word formation examples
Category extension word formation examples Depart word formation
Depart word formation Word formation prefix and suffix
Word formation prefix and suffix Eponyms examples
Eponyms examples Most likely cause
Most likely cause Time factor in soil formation
Time factor in soil formation How does waterfall form
How does waterfall form Lead word formation
Lead word formation Smog
Smog Soap formation reaction
Soap formation reaction