Chapter 8 Solving Second order differential equations numerically


























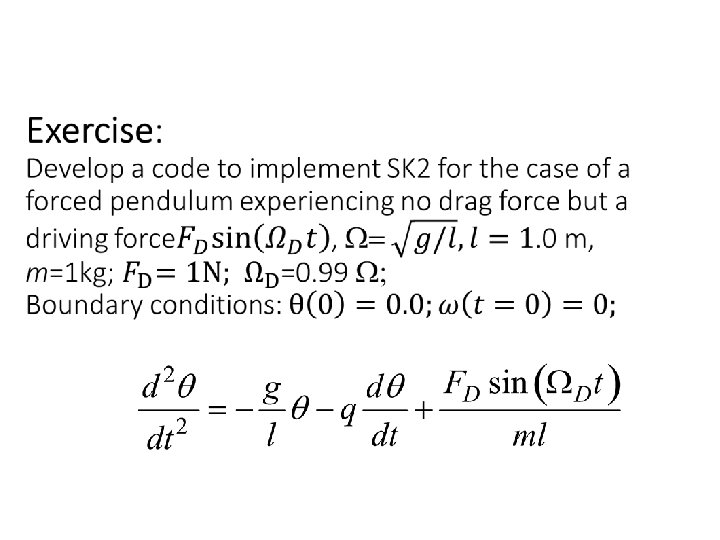

- Slides: 31

Chapter 8 Solving Second order differential equations numerically

Online lecture materials • The online lecture notes by Dr. Tai. Ran Hsu of San José State University, http: //www. engr. sjsu. edu/trhsu/Chapt er%204%20 Second%20 order%20 DEs. p df provides a very clear explanation of the solutions and applications of some typical second order differential equations.





DSolve • DSolve of Mathematica can provide analytical solution to a generic second order differential equation. See Math_built_in_2 ODE. nb.

Typical second order, non-homogeneous ordinary differential equations n(x)

Typical second order, non-homogeneous ordinary differential equations n(x)

Guess: After some algebra


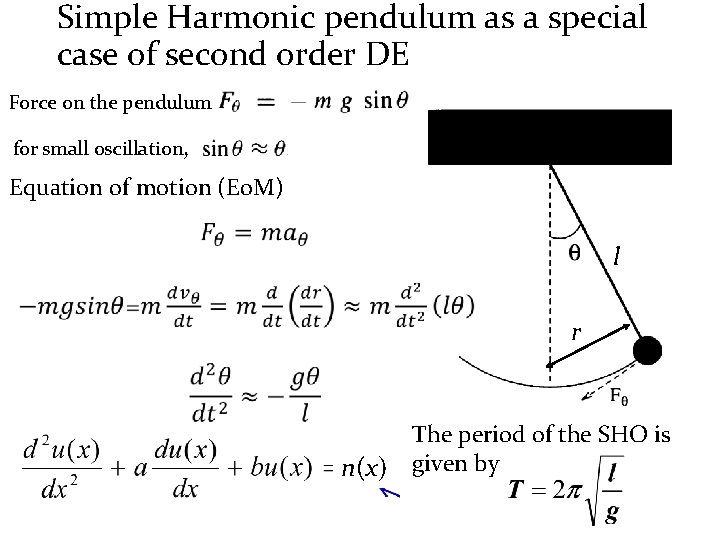
Simple Harmonic pendulum as a special case of second order DE Force on the pendulum for small oscillation, Equation of motion (Eo. M) l r n(x) The period of the SHO is given by

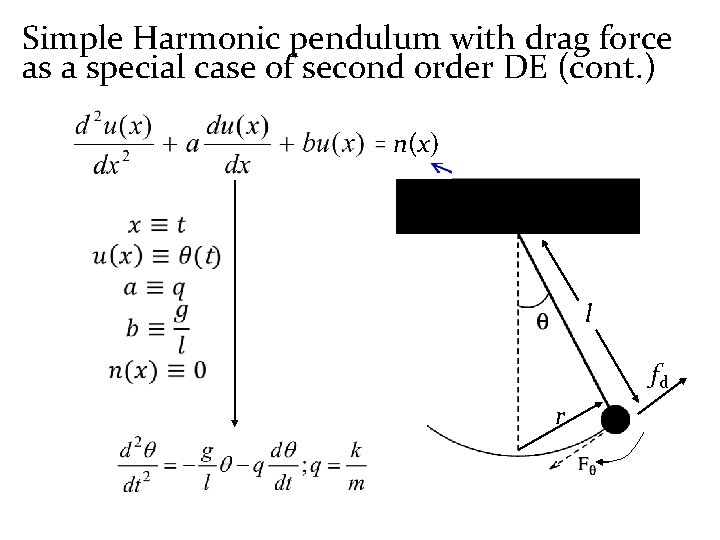
Simple Harmonic pendulum as a special case of second order DE (cont. ) n(x)

Simple Harmonic pendulum as a special case of second order DE (cont. ) Analytical solution:

Simple Harmonic pendulum with drag force as a special case of second order DE Drag force on a moving object, fd = - kv For a pendulum, instantaneous velocity v = wl = l (dq/dt) Hence, fd = - kl (dq/dt). l The net force on the forced pendulum along the tangential direction - kl (dq/dt). fd r

Simple Harmonic pendulum with drag force as a special case of second order DE (cont. ) n(x) l fd r

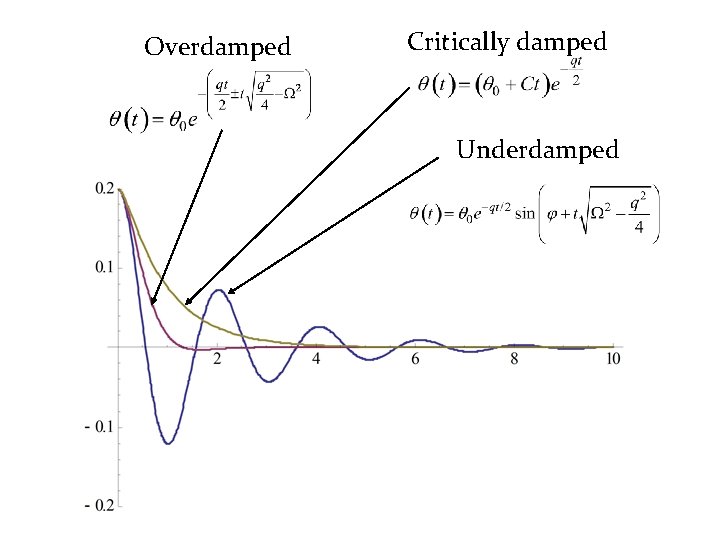
Underdamped regime (small damping). Still oscillate, but amplitude decay slowly over many period before dying totally. Overdamped regime (very large damping), decay slowly over several period before dying totally. q is dominated by exponential term. Analytical solution Critically damped regime, intermediate between under- and overdamping case.

Overdamped Critically damped Underdamped

See 2 ODE_Pendulum. nb where DSolve solves the three cases of a damped pendulum analytically.

Adding driving force to the damped oscillator: forced oscillator - kl (dq/dt) + FD sin(WDt) WD frequency of the applied force

Analytical solution Resonance happens when

Forced oscillator: An example of non homogeneous 2 nd order DE n(x)

Exercise: Forced oscillator

Second order Runge-Kutta (RK 2) method Consider a generic second order differential equation. It can be numerically solved using second order Runge-Kutta method. First, split the second order DE into two first order parts:

Algorithm Set boundary conditions: u(x=x 0)=u 0, u’(x=x 0)=v 0. calculate

Translating the SK 2 algorithm into the case of simple pendulum Set boundary conditions: u(x=x 0)=u 0, u’(x=x 0)=v 0 Set boundary conditions: q(t=t 0)= q 0, q’ (t=t 0)=w 0

Exercise: Develop a code to implement SK 2 for the case of the simple pendulum. Boundary conditions: See pendulum_RK 2. nb

Translating the SK 2 algorithm into the case of damped pendulum Set boundary conditions: u(x=x 0)=u 0, u’(x=x 0)=v 0 Set boundary conditions: q(t=t 0)= q 0, q’ (t=t 0)=w 0

See pendulum_RK 2. nb
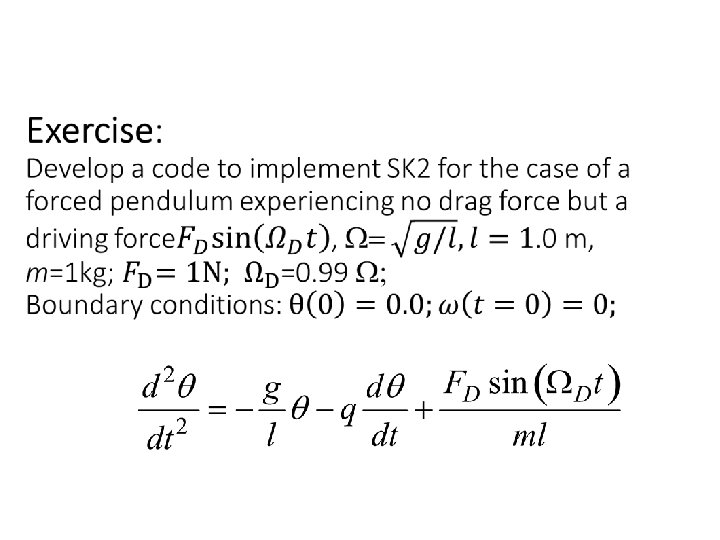

Exercise: Stability of the total energy a SHO in RK 2.
 How to solve second order differential equations
How to solve second order differential equations Euler's differential equation
Euler's differential equation Find the general solution of the differential equation
Find the general solution of the differential equation Integrating factor of differential equation
Integrating factor of differential equation What is a first order equation
What is a first order equation Wolfram alpha phase portrait
Wolfram alpha phase portrait Second order differential equation
Second order differential equation Second order differential equation pendulum
Second order differential equation pendulum First order pde
First order pde First order ordinary differential equations
First order ordinary differential equations Nonlinear ordinary differential equations
Nonlinear ordinary differential equations Separable partial differential equations
Separable partial differential equations Variable separable
Variable separable Higher order linear differential equations
Higher order linear differential equations First order vs second order change
First order vs second order change First order cybernetics and second order cybernetics
First order cybernetics and second order cybernetics Highest order chapter 1
Highest order chapter 1 First order differential equation chapter 9
First order differential equation chapter 9 1st order 2nd order 3rd order neurons
1st order 2nd order 3rd order neurons Substernal notch
Substernal notch The numerically indexed array of php starts with position
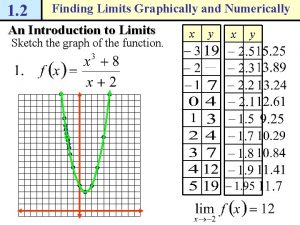
The numerically indexed array of php starts with position Lesson 2 understanding limits graphically and numerically
Lesson 2 understanding limits graphically and numerically Finding limits graphically
Finding limits graphically Finding limits graphically and numerically
Finding limits graphically and numerically Finding limits graphically and numerically worksheet
Finding limits graphically and numerically worksheet Finding limits graphically
Finding limits graphically Lesson 2 understanding limits graphically and numerically
Lesson 2 understanding limits graphically and numerically Topic 9 solving quadratic equations
Topic 9 solving quadratic equations Chapter 1 solving equations and inequalities answers
Chapter 1 solving equations and inequalities answers Linear equations
Linear equations Chapter 1 solving linear equations
Chapter 1 solving linear equations Chapter 1 solving equations and inequalities answers
Chapter 1 solving equations and inequalities answers