First Order Partial Differential Equations Method of characteristics

First Order Partial Differential Equations Method of characteristics Web Lecture WI 2607 -2008 H. M. Schuttelaars 01 November 2020 1 Delft Institute of Applied Mathematics

Contents • Linear First Order Partial Differential Equations Ø Derivation of the Characteristic Equation Ø Examples (solved using Maple) • Quasi-Linear Partial Differential Equations • Nonlinear Partial Differential Equations Ø Derivation of Characteristic Equations Ø Example 01 November 2020 2

Contents • Linear First Order Partial Differential Equations Ø Derivation of the Characteristic Equation Ø Examples (solved using Maple) • Quasi-Linear Partial Differential Equations • Nonlinear Partial Differential Equations Ø Derivation of Characteristic Equations Ø Example 01 November 2020 3

Contents • Linear First Order Partial Differential Equations Ø Derivation of the Characteristic Equation Ø Examples (solved using Maple) After this lecture: • you can recognize a linear first order PDE • you can write down the corresponding characteristic equations • you can parameterize the initial condition and solve the characteristic equation using the initial condition, either analytically or using Maple 01 November 2020 4

First Order Linear Partial Differential Equations Definition of a first order linear PDE: 01 November 2020 5

First Order Linear Partial Differential Equations Definition of a first order linear PDE: 01 November 2020 6

First Order Linear Partial Differential Equations Definition of a first order linear PDE: This is the directional derivative of u in the direction <a, b> 01 November 2020 7

First Order Linear Partial Differential Equations Example 01 November 2020 8

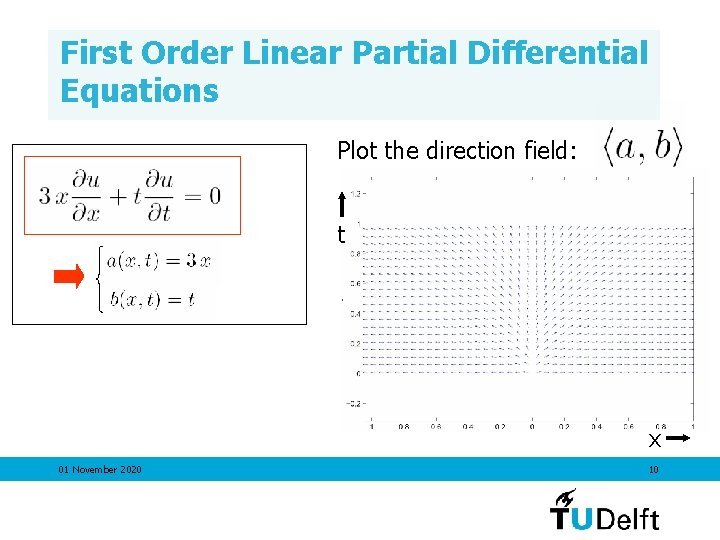
First Order Linear Partial Differential Equations Plot the direction field: 01 November 2020 9

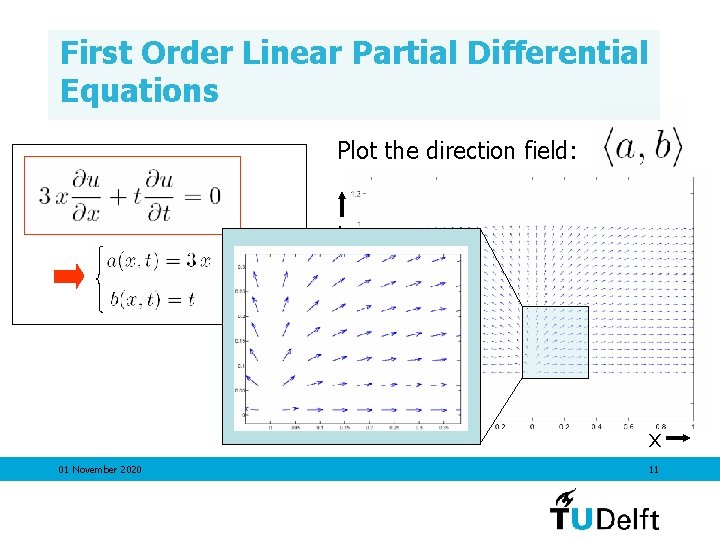
First Order Linear Partial Differential Equations Plot the direction field: t x 01 November 2020 10

First Order Linear Partial Differential Equations Plot the direction field: t x 01 November 2020 11

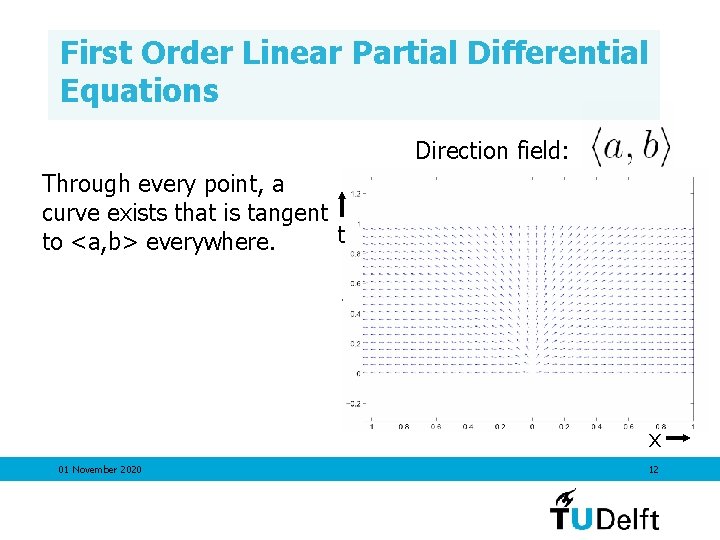
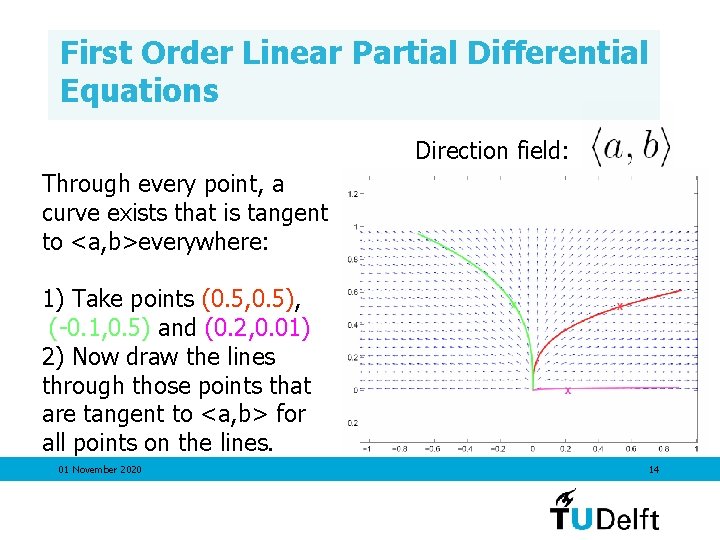
First Order Linear Partial Differential Equations Direction field: Through every point, a curve exists that is tangent t to <a, b> everywhere. x 01 November 2020 12

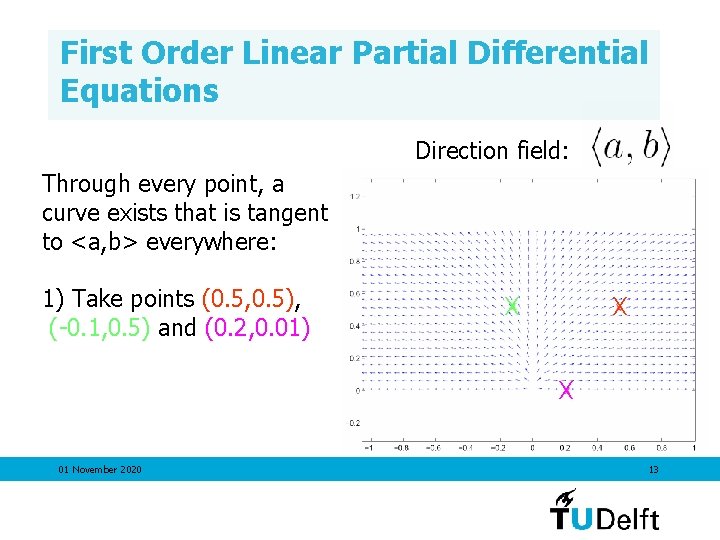
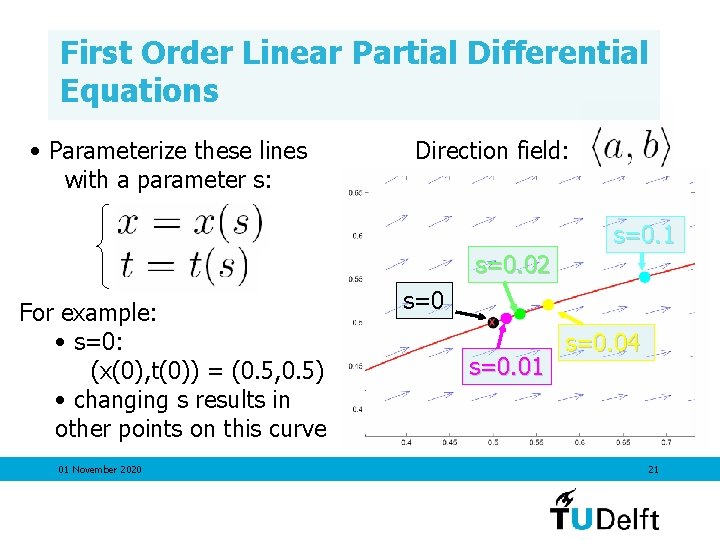
First Order Linear Partial Differential Equations Direction field: Through every point, a curve exists that is tangent to <a, b> everywhere: 1) Take points (0. 5, 0. 5), (-0. 1, 0. 5) and (0. 2, 0. 01) X X X 01 November 2020 13

First Order Linear Partial Differential Equations Direction field: Through every point, a curve exists that is tangent to <a, b>everywhere: 1) Take points (0. 5, 0. 5), (-0. 1, 0. 5) and (0. 2, 0. 01) 2) Now draw the lines through those points that are tangent to <a, b> for all points on the lines. 01 November 2020 14

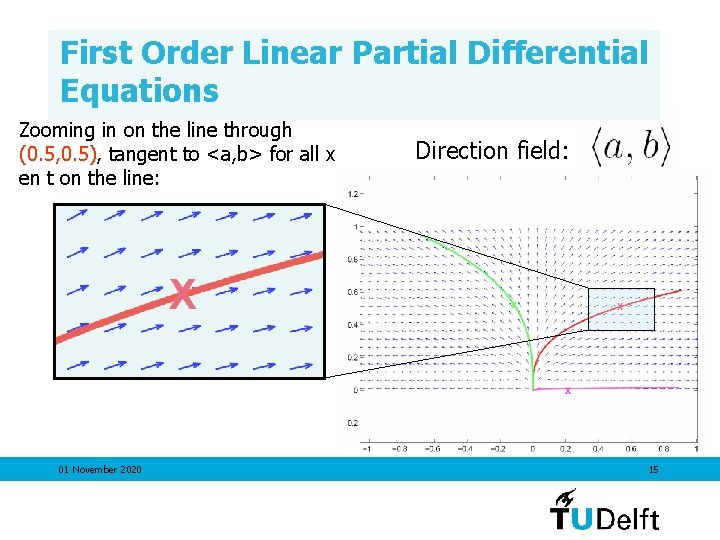
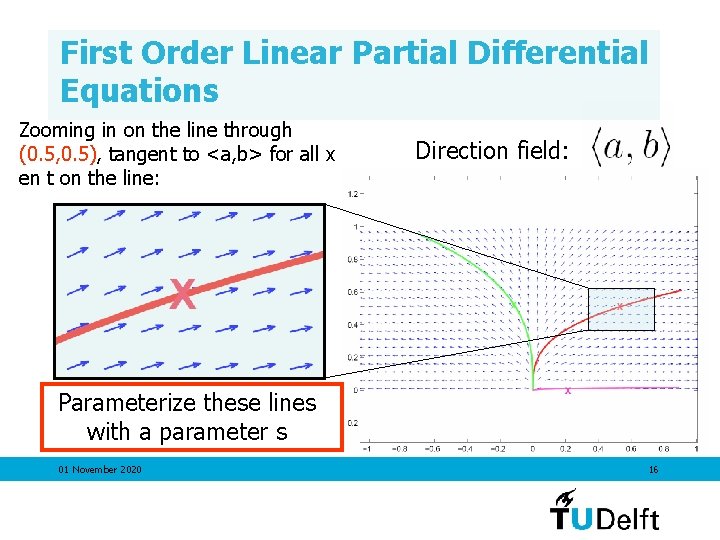
First Order Linear Partial Differential Equations Zooming in on the line through (0. 5, 0. 5), tangent to <a, b> for all x en t on the line: 01 November 2020 Direction field: 15

First Order Linear Partial Differential Equations Zooming in on the line through (0. 5, 0. 5), tangent to <a, b> for all x en t on the line: Direction field: Parameterize these lines with a parameter s 01 November 2020 16

First Order Linear Partial Differential Equations SHORT INTERMEZZO 01 November 2020 17

First Order Linear Partial Differential Equations SHORT INTERMEZZO Parameterization of a line in 2 dimensions Parameter representation of a circle 01 November 2020 18

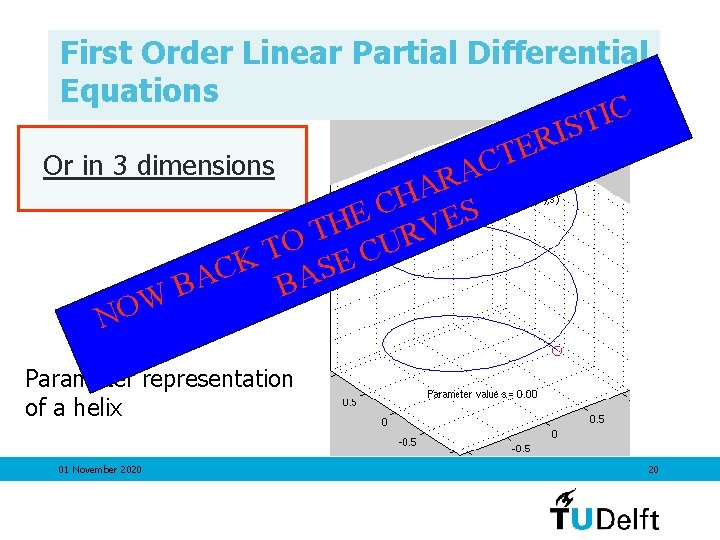
First Order Linear Partial Differential Equations Or in 3 dimensions Parameter representation of a helix 01 November 2020 19

First Order Linear Partial Differential Equations C I T S I R E T C Or in 3 dimensions A R A H S C E E H V T R O U T C K E S C A A B B W NO Parameter representation of a helix 01 November 2020 20

First Order Linear Partial Differential Equations • Parameterize these lines with a parameter s: Direction field: s=0. 1 s=0. 02 For example: • s=0: (x(0), t(0)) = (0. 5, 0. 5) • changing s results in other points on this curve 01 November 2020 s=0. 01 s=0. 04 21

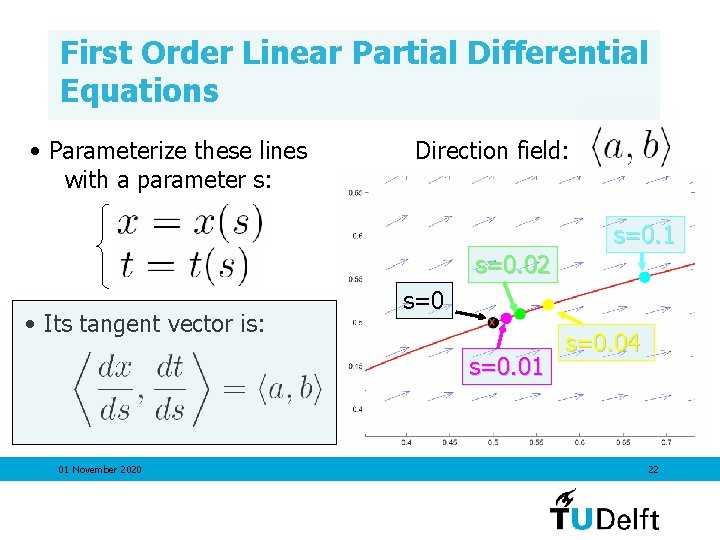
First Order Linear Partial Differential Equations • Parameterize these lines with a parameter s: Direction field: s=0. 1 s=0. 02 • Its tangent vector is: s=0. 01 01 November 2020 s=0. 04 22

First Order Linear Partial Differential Equations • Parameterize these lines with a parameter s, x=x(s), t=t(s). • Its tangent vector is given by • On the curve: 01 November 2020 23

First Order Linear Partial Differential Equations • Parameterize these lines with a parameter s, x=x(s), t=t(s). • Its tangent vector is given by • On the curve: 01 November 2020 24

First Order Linear Partial Differential Equations • Parameterize these lines with a parameter s, x=x(s), t=t(s). • Its tangent vector is given by • On the curve: 01 November 2020 25

First Order Linear Partial Differential Equations • Its tangent vector is given by • On the curve: IN WORDS: THE PDE REDUCES TO AN ODE ON THE CHARACTERISTIC CURVES 01 November 2020 26

First Order Linear Partial Differential Equations • The PDE reduces to an ODE on the characteristic curves. • The characteristic equations (that define the characteristic curves) read: 01 November 2020 27

First Order Linear Partial Differential Equations • The PDE reduces to an ODE on the characteristic curves. • The characteristic equations (that define the characteristic curves) read: One can solve for x(s) and t(s) without solving for u(s). 01 November 2020 28

First Order Linear Partial Differential Equations • The PDE reduces to an ODE on the characteristic curves. • The characteristic equations (that define the characteristic curves) read: One can solve for x(s) Gives the characteristic and t(s) without solving base curves for u(s). 01 November 2020 29

First Order Linear Partial Differential Equations The equations for the characteristic base were solved to get the base curves in the example: Solving 01 November 2020 30

First Order Linear Partial Differential Equations The equations for the characteristic base were solved to get the base curves in the example: Solving 01 November 2020 gives 31

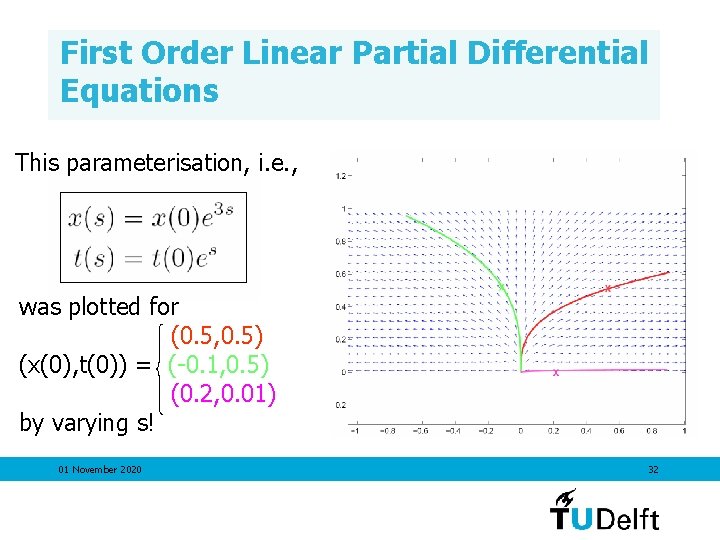
First Order Linear Partial Differential Equations This parameterisation, i. e. , was plotted for (0. 5, 0. 5) (x(0), t(0)) = (-0. 1, 0. 5) (0. 2, 0. 01) by varying s! 01 November 2020 32

First Order Linear Partial Differential Equations To solve the original PDE, u(x, t) has to be prescribed at a certain curve C =C (x, t). 01 November 2020 33

First Order Linear Partial Differential Equations To solve the original PDE, u(x, t) has to be prescribed at a certain curve C =C (x, t). The corresponding system of ODE’s has to be solved such that u(x, t) has the prescribed value at this curve C. 01 November 2020 34

First Order Linear Partial Differential Equations The corresponding system of ODE’s has to be solved such that u(x, t) has the prescribed value at this curve C. • As a first step, parameterize the initial curve C with the parameter τ: x=x(τ), t=t(τ) and u=u(τ). 01 November 2020 35

First Order Linear Partial Differential Equations The corresponding system of ODE’s has to be solved such that u(x, t) has the prescribed value at this curve C. • As a first step, parameterize the initial curve C with the parameter τ: x=x(τ), t=t(τ) and u=u(τ). • Next, the family of characteristic curves, determined by the points on C , may be parameterized by x=x(s, τ), t=t(x, τ) and u=u(s, τ), with the initial conditions prescribed for s=0. 01 November 2020 36

First Order Linear Partial Differential Equations • As a first step, parameterize the initial curve C with the parameter τ: x=x(τ), t=t(τ) and u=u(τ). • Next, the family of characteristic curves, determined by the points on C , may be parameterized by x=x(s, τ), t=t(x, τ) and u=u(s, τ), with the initial conditions prescribed for s=0. This gives the solution surface 01 November 2020 37

First Order Linear Partial Differential Equations EXAMPLE 1 01 November 2020 38

First Order Linear Partial Differential Equations • Consider with The corresponding PDE reads: 01 November 2020 39

First Order Linear Partial Differential Equations • Consider with • Parameterize this initial curve with parameter l: 01 November 2020 40

First Order Linear Partial Differential Equations • Consider with • Parameterize this initial curve with parameter l: • Solve the characteristic equations with these initial conditions. 01 November 2020 41

First Order Linear Partial Differential Equations • Consider with • The (parameterized) solution reads: 01 November 2020 42

First Order Linear Partial Differential Equations Visualize the solution for various values of l: 01 November 2020 43

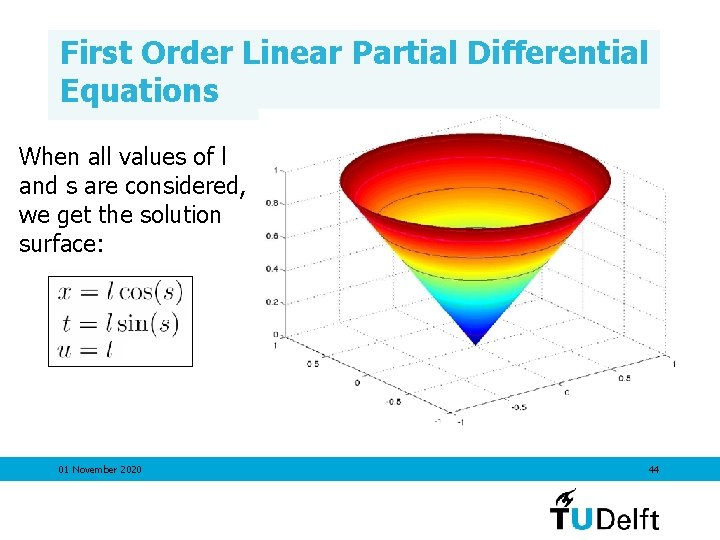
First Order Linear Partial Differential Equations When all values of l and s are considered, we get the solution surface: 01 November 2020 44

First Order Linear Partial Differential Equations EXAMPLE 2 01 November 2020 45

First Order Linear Partial Differential Equations PDE: Initial condition: 01 November 2020 46

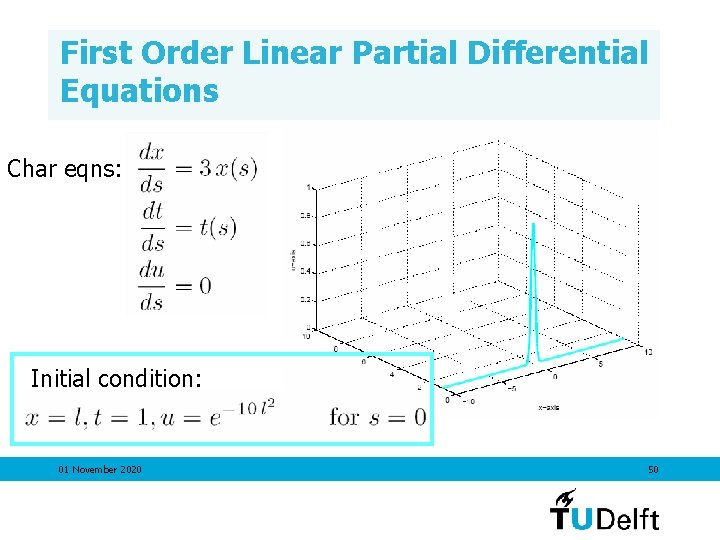
First Order Linear Partial Differential Equations PDE: Initial condition: Char eqns: 01 November 2020 47

First Order Linear Partial Differential Equations PDE: Initial condition: Char eqns: Parameterised initial condition: 01 November 2020 48

First Order Linear Partial Differential Equations Char eqns: Parameterized initial condition: Parameterized solution: 01 November 2020 49

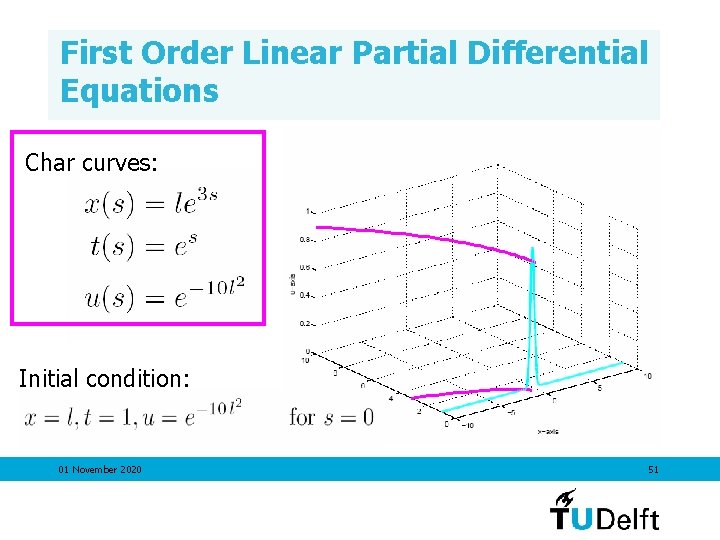
First Order Linear Partial Differential Equations Char eqns: Initial condition: 01 November 2020 50

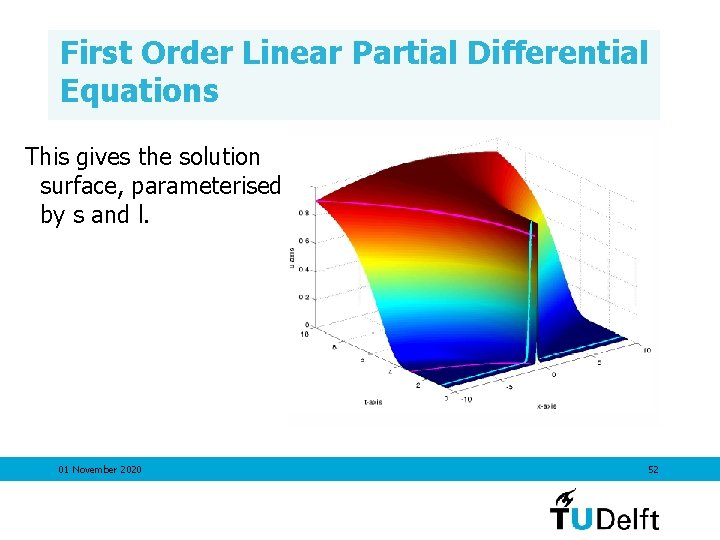
First Order Linear Partial Differential Equations Char curves: Initial condition: 01 November 2020 51

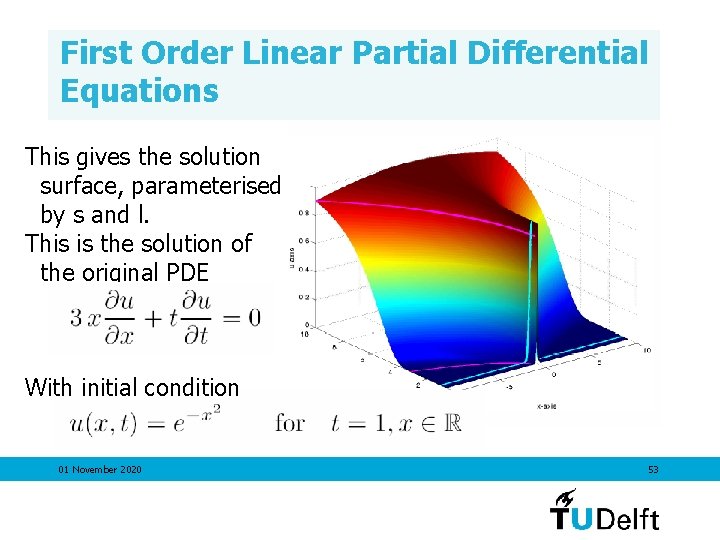
First Order Linear Partial Differential Equations This gives the solution surface, parameterised by s and l. 01 November 2020 52

First Order Linear Partial Differential Equations This gives the solution surface, parameterised by s and l. This is the solution of the original PDE With initial condition 01 November 2020 53

First Order Linear Partial Differential Equations Recipe to solve the PDE 1. To solve the partial differential equation explicitly, u(x, t) must be given at a certain curve C. As a first step, parameterize this curve with parameter l. 01 November 2020 54

First Order Linear Partial Differential Equations 2. Write down the characteristic equations, note that x, t and u now depend on both the parameters s and l. 01 November 2020 55

First Order Linear Partial Differential Equations 3. Solve the characteristic equations, using the conditions on the curve C. Take s=0 at this curve. Hence x, t and u are obtained as functions of s and l. 01 November 2020 56

First Order Linear Partial Differential Equations 3. Solve the characteristic equations, using the conditions on the curve C. Take s=0 at this curve. Hence x, t and u are obtained as functions of s and l. 4. To get u in terms of x and t, at least in the neighbourhood of C , explicit expressions for s and l are needed: 01 November 2020 57

First Order Linear Partial Differential Equations 3. Solve the characteristic equations, using the conditions on the curve C. Take s=0 at this curve. Hence x, t and u are obtained as functions of s and l. 4. To get u in terms of x and t, at least in the neighbourhood of C , explicit expressions for s and l are needed: Implicit Function Theorem: possible in a neighborhood of C if 01 November 2020 58

First Order Linear Partial Differential Equations 3. Solve the characteristic equations, using the conditions on the curve C. Take s=0 at this curve. Hence x, t and u are obtained as functions of s and l. 4. To get u in terms of x and t, at least in the neighbourhood of C , explicit expressions for s and l are needed: (Implicit Function Theorem) • possible in a neighborhood of C if • otherwise: no solution of infinitely many solutions 01 November 2020 59

First Order Linear Partial Differential Equations EXAMPLE 3 (using Maple) 01 November 2020 60

First Order Linear Partial Differential Equations Consider the PDV with initial condition 01 November 2020 61

First Order Linear Partial Differential Equations Consider the PDV with initial condition Visualize the IC using 01 November 2020 62

First Order Linear Partial Differential Equations Consider the PDV with initial condition Write down the characteristic equations 01 November 2020 63

First Order Linear Partial Differential Equations Consider the PDV with initial condition Solve the characteristic equations using dsolve: 01 November 2020 64

First Order Linear Partial Differential Equations Consider the PDV with initial condition Solve the characteristic equations using dsolve: 01 November 2020 65

First Order Linear Partial Differential Equations Use the solution sol to vizualize the solution surface: Note that in this example we can easily find s and l in terms of x and t and hence get the solution in terms of x and t: s=t l = x-t 01 November 2020 66

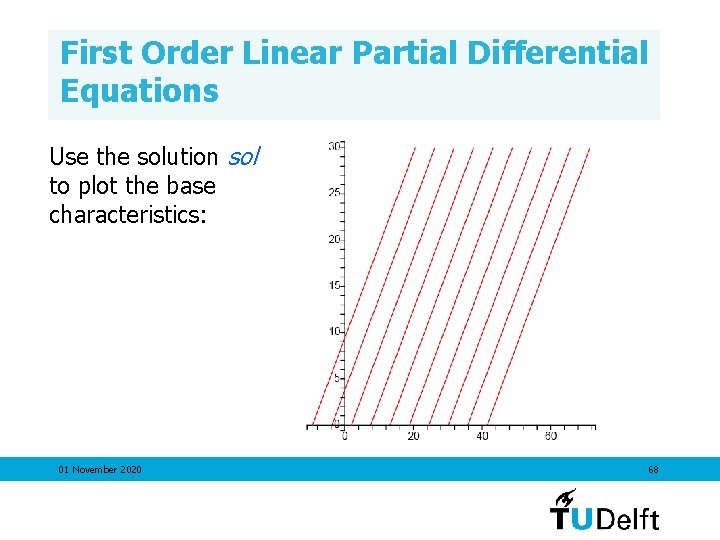
First Order Linear Partial Differential Equations Use the solution sol to plot the base characteristics: 01 November 2020 67

First Order Linear Partial Differential Equations Use the solution sol to plot the base characteristics: 01 November 2020 68

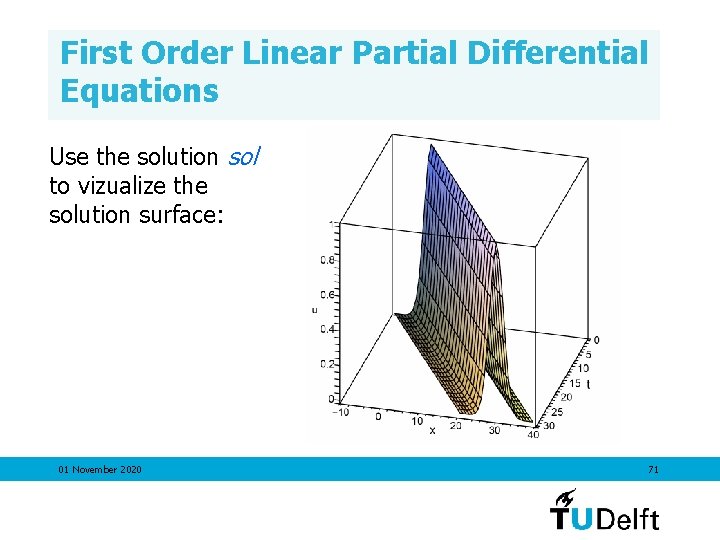
First Order Linear Partial Differential Equations Use the solution sol to vizualize the solution surface: 01 November 2020 69

First Order Linear Partial Differential Equations Use the solution sol to vizualize the solution surface: 01 November 2020 70

First Order Linear Partial Differential Equations Use the solution sol to vizualize the solution surface: 01 November 2020 71

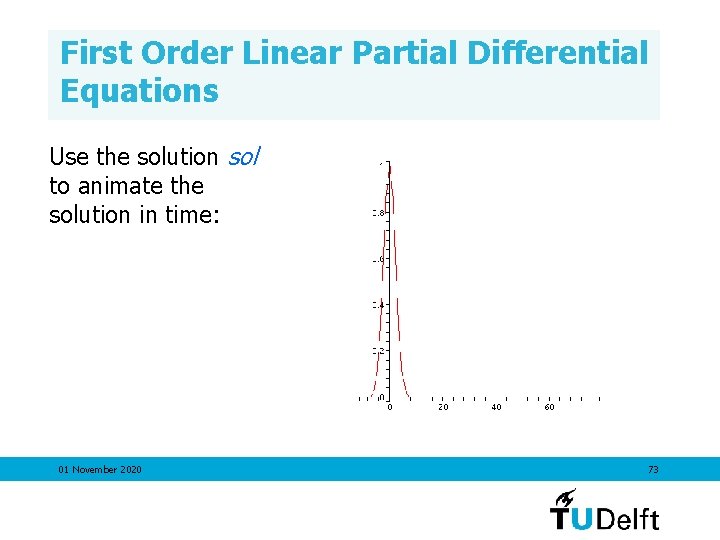
First Order Linear Partial Differential Equations Use the solution sol to animate the solution in time: 01 November 2020 72

First Order Linear Partial Differential Equations Use the solution sol to animate the solution in time: 01 November 2020 73

First Order Linear Partial Differential Equations EXAMPLE 4 (using Maple) 01 November 2020 74

First Order Linear Partial Differential Equations Consider the PDV with initial condition 01 November 2020 75

First Order Linear Partial Differential Equations Consider the PDV with initial condition Write down the characteristic equations 01 November 2020 76

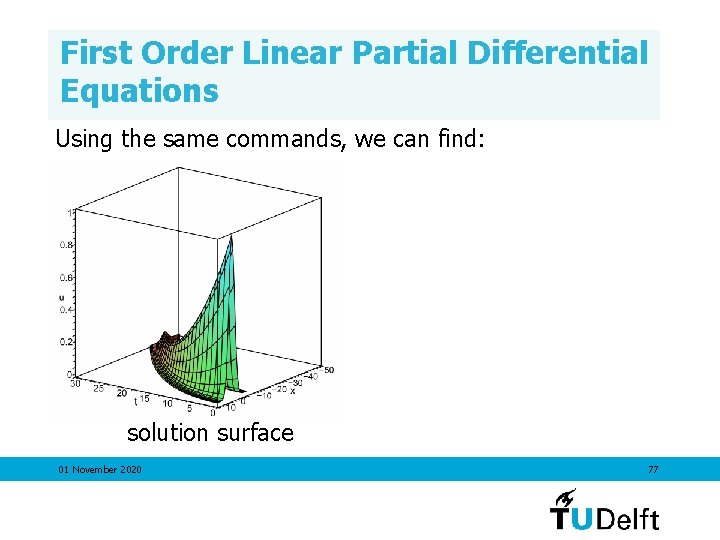
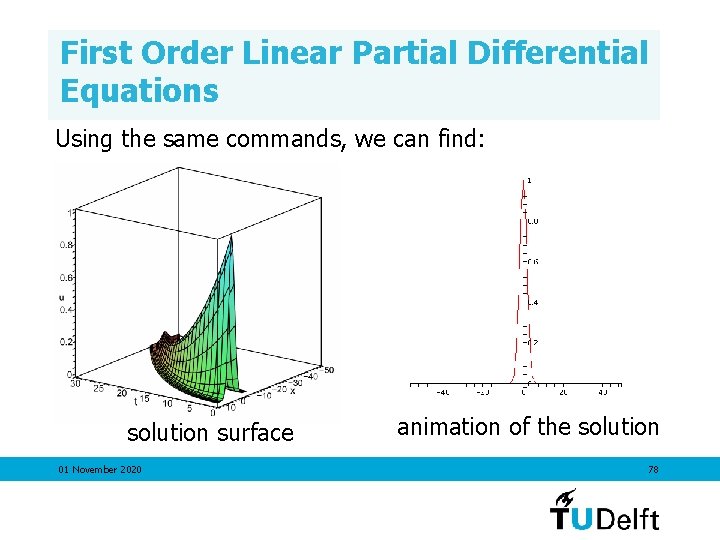
First Order Linear Partial Differential Equations Using the same commands, we can find: solution surface 01 November 2020 77

First Order Linear Partial Differential Equations Using the same commands, we can find: solution surface 01 November 2020 animation of the solution 78

Conclusions You are able to: • you can recognize a linear first order PDE • you can write down the corresponding characteristic equations • you can parameterize the initial condition and solve the characteristic equation using the initial condition, either analytically or using Maple 01 November 2020 79

Conclusions You are able to: • you can recognize a linear first order PDE • you can write down the corresponding characteristic equations • you can parameterize the initial condition and solve the characteristic equation using the initial condition, either analytically or using Maple Next lecture: • quasi-linear first order partial differential equations 01 November 2020 80