Linear Differential Equations with Constant Coefficients ft m




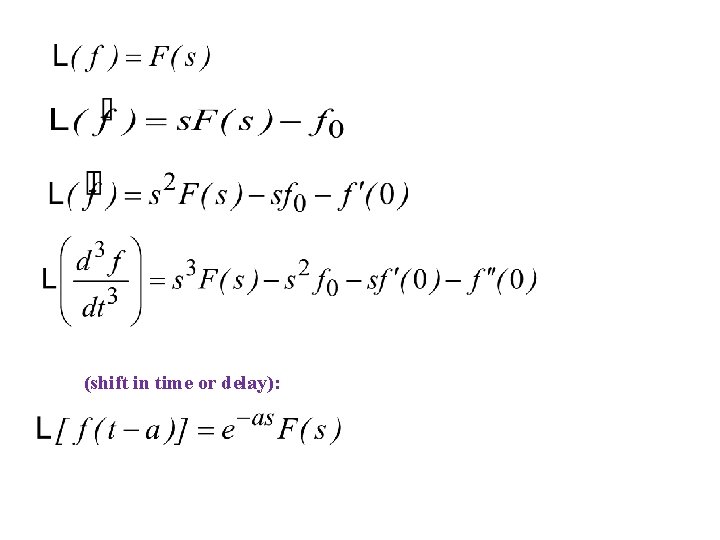

![Partial fraction expansion: With Matlab; num=[-1. 2, -2. 3, -9. 9]; den=[1, 4, 14, Partial fraction expansion: With Matlab; num=[-1. 2, -2. 3, -9. 9]; den=[1, 4, 14,](https://slidetodoc.com/presentation_image_h/b6ba8594232895fd7ee3cb0e7f26b411/image-8.jpg)



- Slides: 12

Linear Differential Equations with Constant Coefficients: f(t) m k x(t) Assume c If (No oscillation) Different two roots If (No oscillation) Repeated roots Homogeneous Form If (x(t) depends on the initial conditions) (Oscillatory response) Complex roots (Characteristic polynomial) The form of the system response is determined by the eigenvalues of the system which are determined by m, c and k. Critical damping coefficient (Damping ratio)

f(t): Input Example: u(t): Output (response) Homogeneous solution f(t)=0. u(t)=est Characteristic Equation: With Matlab: s 3 est + 4 s 2 est + 14 sest + 20 est= 0 s 3 + 4 s 2 + 14 s + 20 = 0 uh(t) = C 1 e(-1+3 i)t + C 2 e(-1 -3 i)t + A 2 e-2 t uh(t) = A 1 e-tcos(3 t-φ)+A 2 e-2 t a=[1, 4, 14, 20]; roots(a) Eigenvalues: -1 3 i, - 2

uh(t) = A 1 e-tcos(3 t-φ)+A 2 e-2 t Initial conditions: at t=0 -1. 2 = A 1 cosφ + A 2 2. 5 = -A 1 cosφ +3 A 1 sinφ -2 A 2 -3. 1= -8 A 1 cosφ - 6 A 1 sinφ + 4 A 2 A 1, A 2 and φ can be found by Newton-Raphson method.

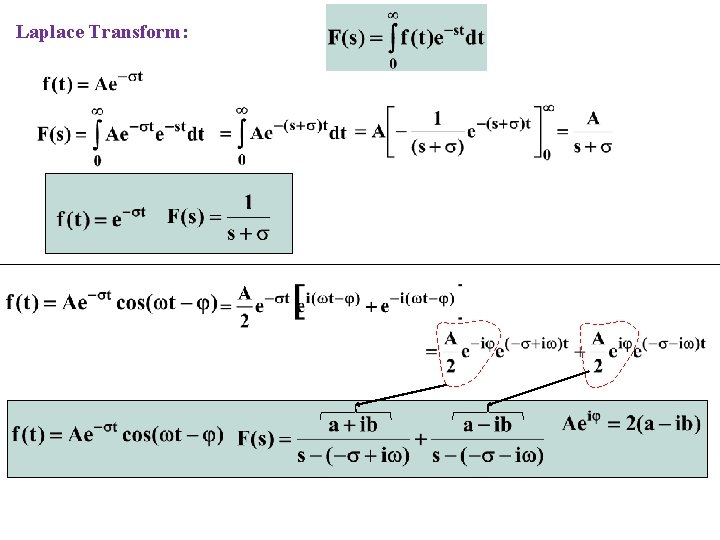
Laplace Transform:

Laplace Transform of the Derivatives :
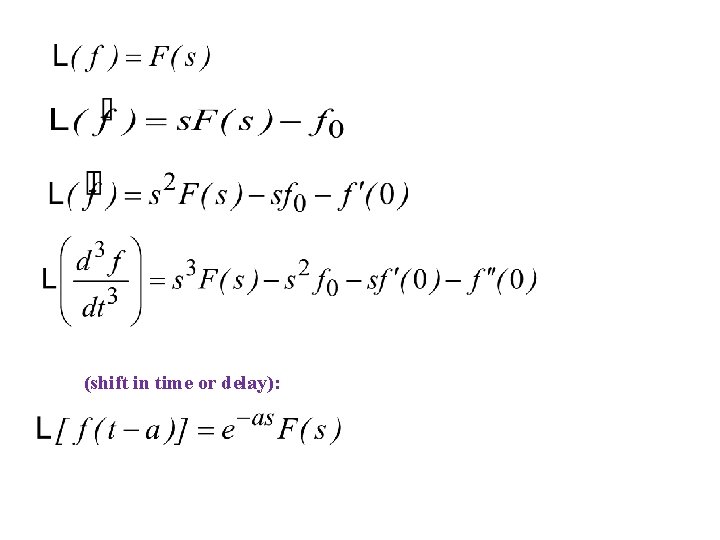
(shift in time or delay):

Laplace transform of the solution due to the initial conditions: Initial conditions: at t=0
![Partial fraction expansion With Matlab num1 2 2 3 9 9 den1 4 14 Partial fraction expansion: With Matlab; num=[-1. 2, -2. 3, -9. 9]; den=[1, 4, 14,](https://slidetodoc.com/presentation_image_h/b6ba8594232895fd7ee3cb0e7f26b411/image-8.jpg)
Partial fraction expansion: With Matlab; num=[-1. 2, -2. 3, -9. 9]; den=[1, 4, 14, 20]; [r, p, k]=residue(num, den) r(1)=-0. 095 -0. 0483 i, r(2)=-0. 095+0. 0483 i, r(3)=-1. 01

Homogeneous solution : uh(t) = A 1 e-tcos(3 t-φ)+A 2 e-2 t With Matlab; z=-0. 095+0. 0483 i A 1=2*abs(z) fi=angle(z)

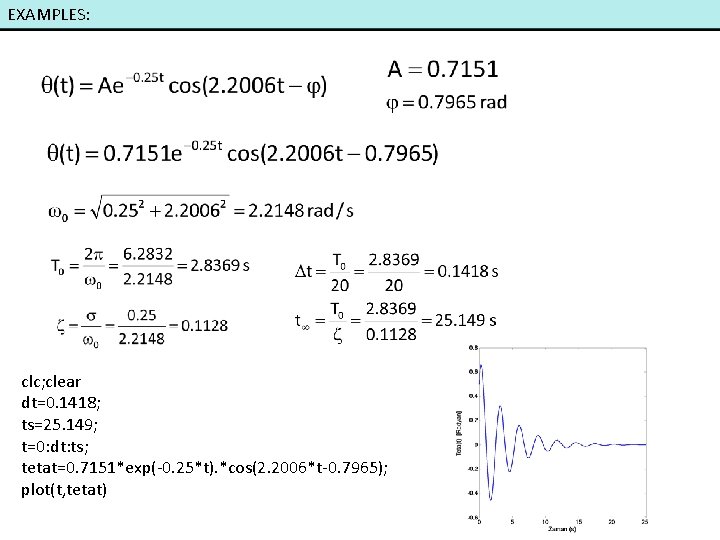
EXAMPLES: Joint friction, B g L The equation of the motion for the unforced motion of a simple pendulum is given as: m=2 kg θ B=4 Nms/rad m L=2 m Applying the Laplace transform, At t=0 are given. Find θ(t).

EXAMPLES: Laplace transform of the homogenous solution (due to the initial conditions) Eigenvalues The system is stable because the real parts of all the roots are negative. clc; clear num=[4 10]; den=[8 4 39. 24]; [r, p, k]=residue(num, den) r(2) A=2*abs(r(2)) Fi=angle(r(2)) 0. 2556 Img 0. 25 Re

EXAMPLES: clc; clear dt=0. 1418; ts=25. 149; t=0: dt: ts; tetat=0. 7151*exp(-0. 25*t). *cos(2. 2006*t-0. 7965); plot(t, tetat)