Differential Equations ordinary differential equations Definition A differential











































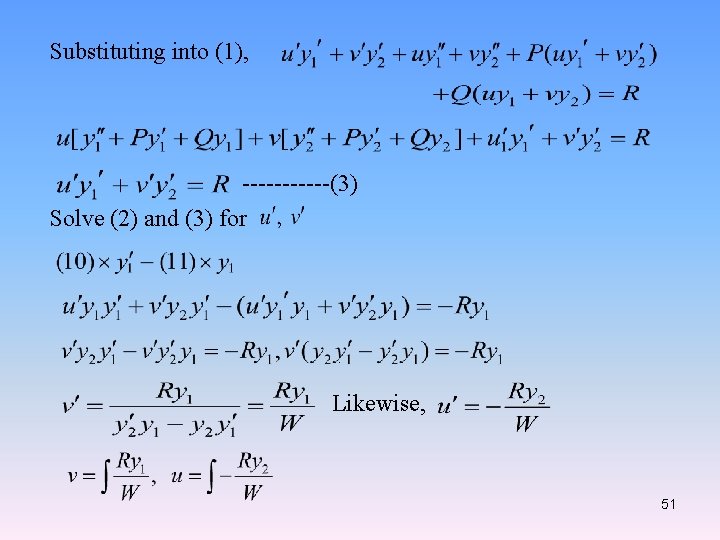

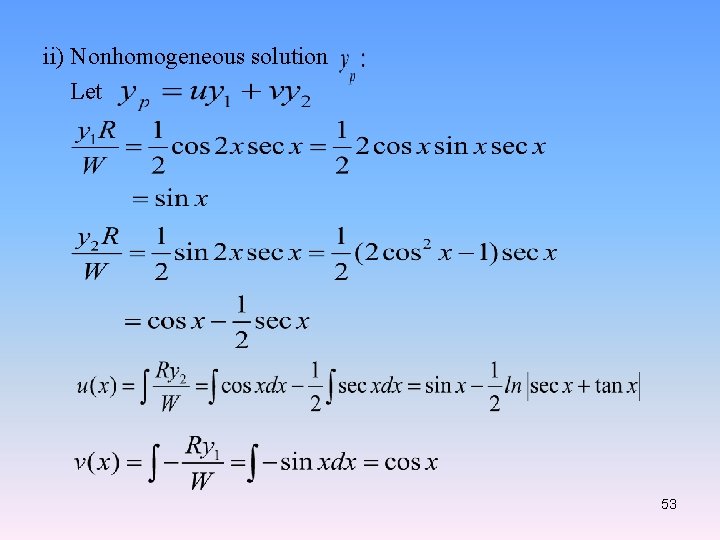
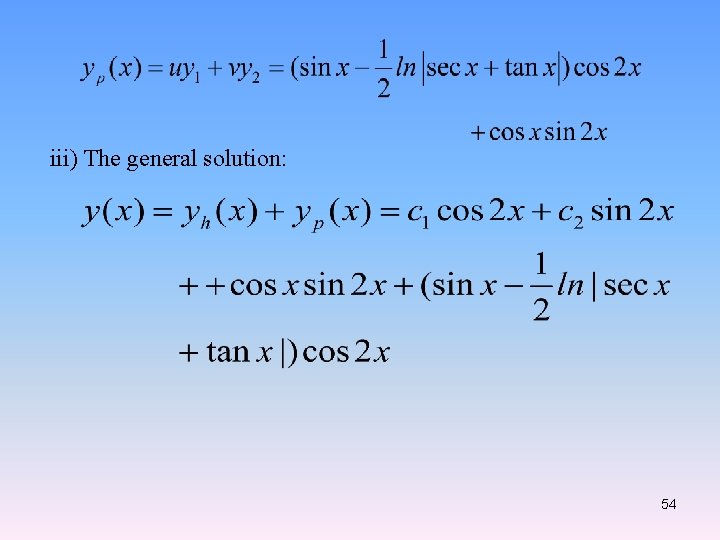
- Slides: 54

Differential Equations

ordinary differential equations Definition: A differential equation is an equation containing an unknown function and its derivatives. Examples: . 1. 2. 3. y is dependent variable and x is independent variable, and these are ordinary differential equations

Partial Differential Equation Examples: 1. u is dependent variable and x and y are independent variables, and is partial differential equation. 2. 3. u is dependent variable and x and t are independent variables

Order of Differential Equation The order of the differential equation is order of the highest derivative in the differential equation. Differential Equation ORDER 1 2 3

Degree of Differential Equation The degree of a differential equation is power of the highest order derivative term in the differential equation. Differential Equation Degree 1 1 3

Linear Differential Equation A differential equation is linear, if 1. dependent variable and its derivatives are of degree one, 2. coefficients of a term does not depend upon dependent variable. Example: 1. is linear. Example: 2. is non - linear because in 2 nd term is not of degree one.

Example: 3. is non - linear because in 2 nd term coefficient depends on y. Example: 4. is non - linear because is non – linear

It is Ordinary/partial Differential equation of order… and of degree…, it is linear / non linear, with independent variable…, and dependent variable….

1 st – order differential equation 1. Derivative form: 2. Differential form: . 3. General form: or Differential Equation Chapter 1 9

First Order Ordinary Differential equation Differential Equation Chapter 1 10

Second order Ordinary Differential Equation Chapter 1 11

nth – order linear differential equation 1. nth – order linear differential equation with constant coefficients. 2. nth – order linear differential equation with variable coefficients Differential Equation Chapter 1 12

Differential Equation Chapter 1 Origin of Differential Equations Solution 1. Geometric Origin 1. For the family of straight lines the differential equation is 2. . For the family of curves A. the differential equation is B. the differential equation is 13

Differential Equation Chapter 1 Physical Origin 1. Newton’s Low of Cooling where is rate of cooling of the liquid, is temperature difference between the liquid ‘T’ and its surrounding Ts 2. Growth and Decay y is the quantity present at any time Differential Equation Chapter 1 14

Solution of Differential Equation Chapter 1 15

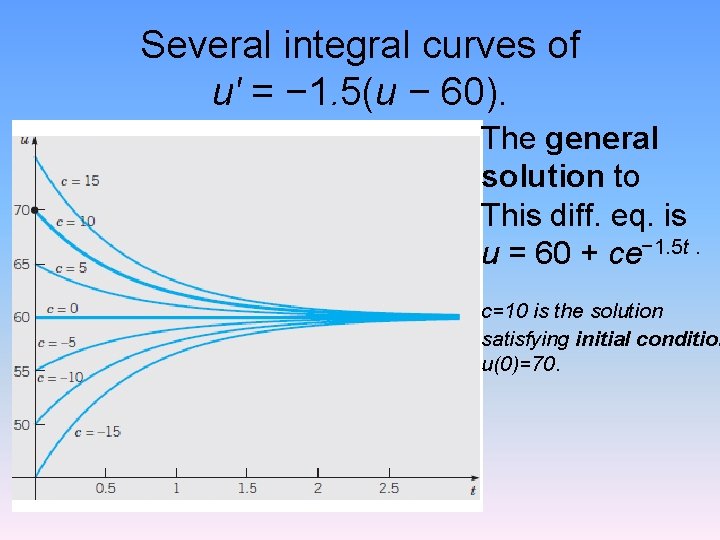
Several integral curves of u' = − 1. 5(u − 60). The general solution to This diff. eq. is u = 60 + ce− 1. 5 t. c=10 is the solution satisfying initial condition u(0)=70.

First order differential equations • No general method of solutions of 1 st O. D. E. s because of their different degrees of complexity. • Possible to classify them as: – exact equations – equations in which the variables can be separated – homogenous equations – equations solvable by an integrating factor

Exact equations • Exact? General solution: F (x, y) = C For example

Separable-variables equations • In the most simple first order differential equations, the independent variable and its differential can be separated from the dependent variable and its differential by the equality sign, using nothing more than the normal processes of elementary algebra. For example

Separable Differential Equations A separable differential equation can be expressed as the product of a function of x and a function of y. Example: Combined constants of integration

Homogeneous equations • Homogeneous? • A differential equation of the type, is termed a homogeneous differential equation of the first order. • Such an equation can be solved by making the substitution u = y/x and thereafter integrating the transformed equation.

Equations solved by integrating factor • There exists a factor by which the equation can be multiplied so that the one side becomes a complete differential equation. The factor is called “the integrating factor”. where P and Q are functions of x only Assuming the integrating factor R is a function of x only, then is the integrating factor

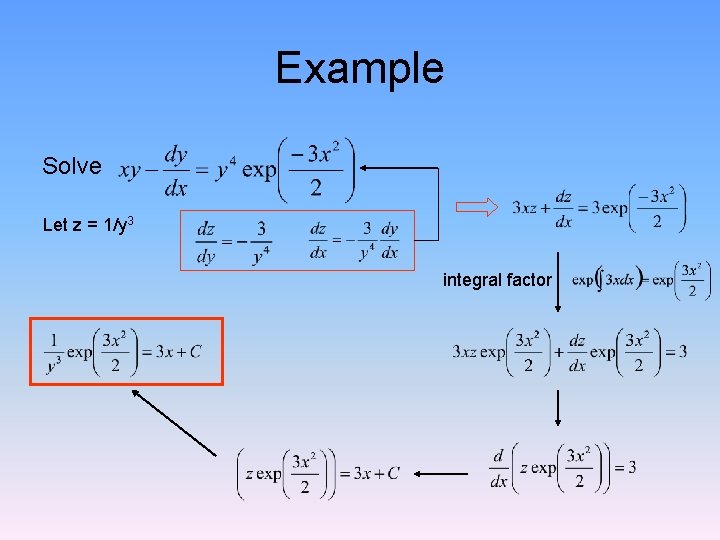
Example Solve Let z = 1/y 3 integral factor

Second-order O. D. E. • Purpose: reduce to 1 st O. D. E. • Likely to be reduced equations: – Non-linear • Equations where the dependent variable does not occur explicitly. • Equations where the independent variable does not occur explicitly. • Homogeneous equations. – Linear • The coefficients in the equation are constant • The coefficients are functions of the independent variable.

Non-linear 2 nd O. D. E. - Equations where the dependent variables does not occur explicitly • They are solved by differentiation followed by the p substitution. • When the p substitution is made in this case, the second derivative of y is replaced by the first derivative of p thus eliminating y completely and producing a first O. D. E. in p and x.

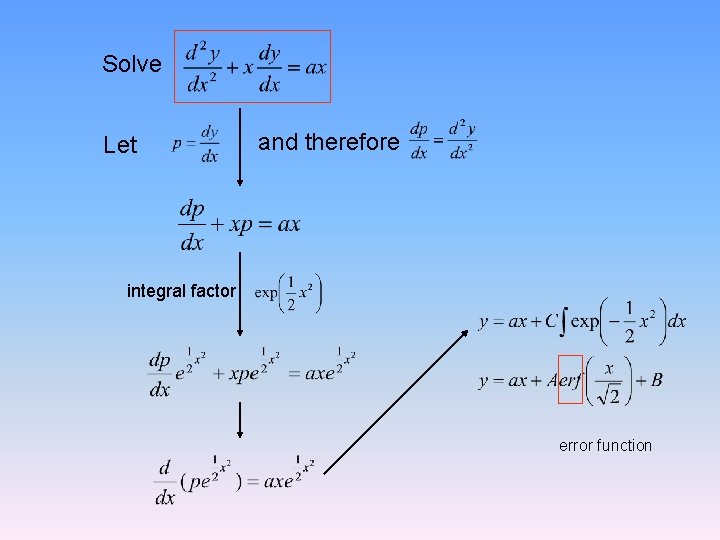
Solve Let and therefore integral factor error function

Non-linear 2 nd O. D. E. - Equations where the independent variables does not occur explicitly • They are solved by differentiation followed by the p substitution. • When the p substitution is made in this case, the second derivative of y is replaced as Let

Solve Let and therefore Separating the variables

Linear differential equations • The general linear differential equation of the nth order having constant coefficients may be written: where (x) is any function of x.

2 nd order linear differential equations The general equation can be expressed in the form where P, Q, and R are constant coefficients Let the dependent variable y be replaced by the sum of the two new variables: y = u + v Therefore If v is a particular solution of the original differential equation The general solution of the linear differential equation will be the sum of a “complementary function” and a “particular solution”. purpose

The complementary function Let the solution assumed to be: auxiliary equation (characteristic equation) Unequal roots Equal roots Real roots Complex roots

Unequal roots to auxiliary equation • Let the roots of the auxiliary equation be distinct and of values m 1 and m 2. Therefore, the solutions of the auxiliary equation are: • The most general solution will be • If m 1 and m 2 are complex it is customary to replace the complex exponential functions with their equivalent trigonometric forms.

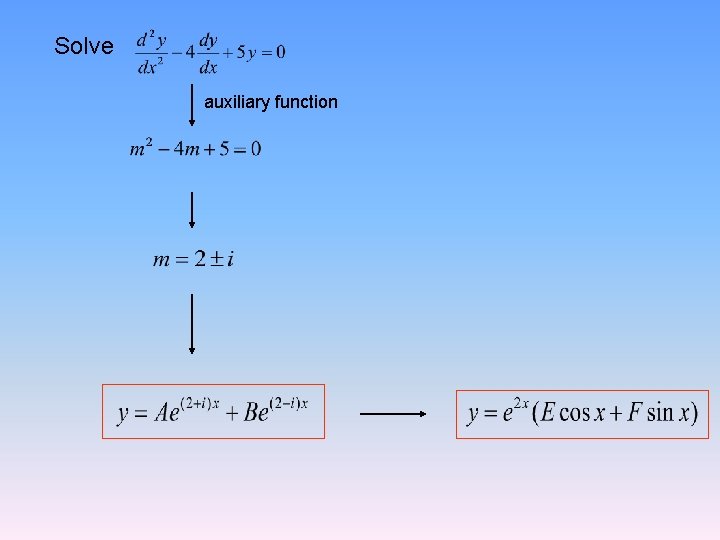
Solve auxiliary function

Equal roots to auxiliary equation • Let the roots of the auxiliary equation equal and of value m 1 = m 2 = m. Therefore, the solution of the auxiliary equation is: Let where V is a function of x

Solve auxiliary function

Solve auxiliary function

Particular integrals • Two methods will be introduced to obtain the particular solution of a second linear O. D. E. – The method of undetermined coefficients • confined to linear equations with constant coefficients and particular form of (x) – The method of inverse operators • general applicability

Method of undetermined coefficients • When (x) is constant, say C, a particular integral of equation is • When (x) is a polynomial of the form where all the coefficients are constants. The form of a particular integral is • When (x) is of the form Terx, where T and r are constants. The form of a particular integral is

Method of undetermined coefficients • When (x) is of the form G sin nx + H cos nx, where G and H are constants, the form of a particular solution is • Modified procedure when a term in the particular integral duplicates a term in the complementary function.

Solve auxiliary equation Equating coefficients of equal powers of x

Method of inverse operators • Sometimes, it is convenient to refer to the symbol “D” as the differential operator: But,

The differential operator D can be treated as an ordinary algebraic quantity with certain limitations. (1) The distribution law: A(B+C) = AB + AC which applies to the differential operator D (2) The commutative law: AB = BA which does not in general apply to the differential operator D Dxy x. Dy (D+1)(D+2)y = (D+2)(D+1)y (3) The associative law: (AB)C = A(BC) which does not in general apply to the differential operator D D(Dy) = (DD)y D(xy) = (Dx)y + x(Dy) The basic laws of algebra thus apply to the pure operators, but the relative order of operators and variables must be maintained.

Differential operator to exponentials More convenient!

Differential operator to trigonometrical functions where “Im” represents the imaginary part of the function which follows it.

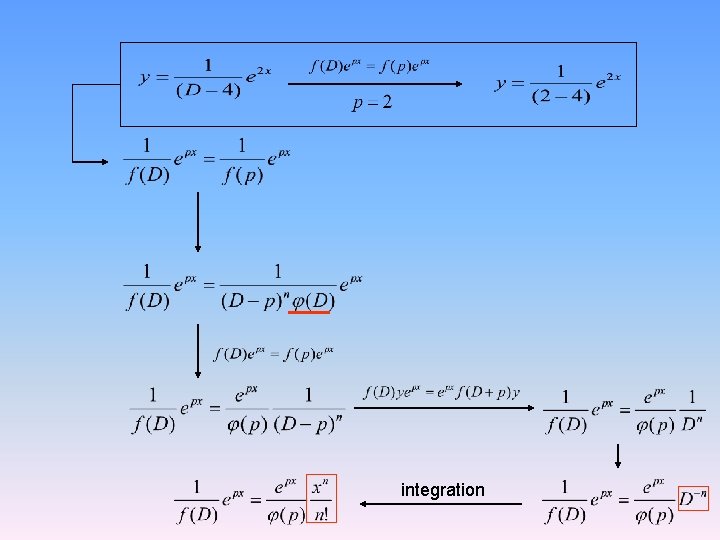
The inverse operator The operator D signifies differentiation, i. e. • D-1 is the “inverse operator” and is an “intergrating” operator. • It can be treated as an algebraic quantity in exactly the same manner as D

Solve differential operator binomial expansion =2

integration

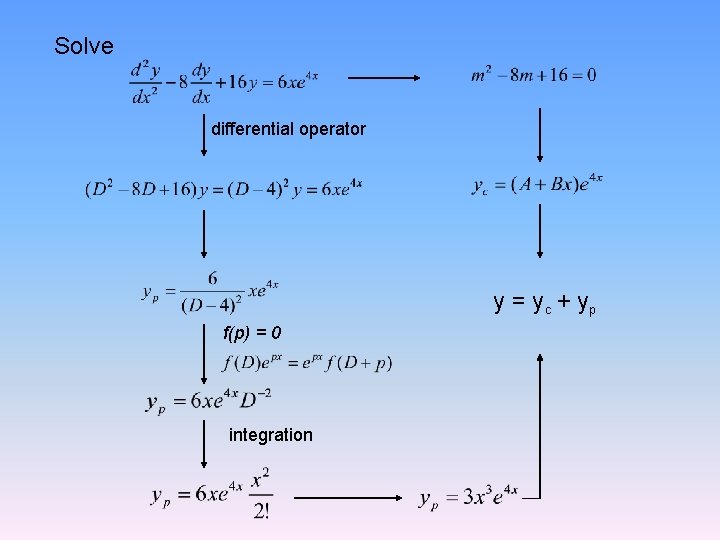
Solve differential operator y = y c + yp f(p) = 0 integration

Solve differential operator y = y c + yp expanding each term by binomial theorem

Variation of parameters ……. (1) The general solution: Replace with homogeneous solution in the general Let Assume …. . (2) Compute 50
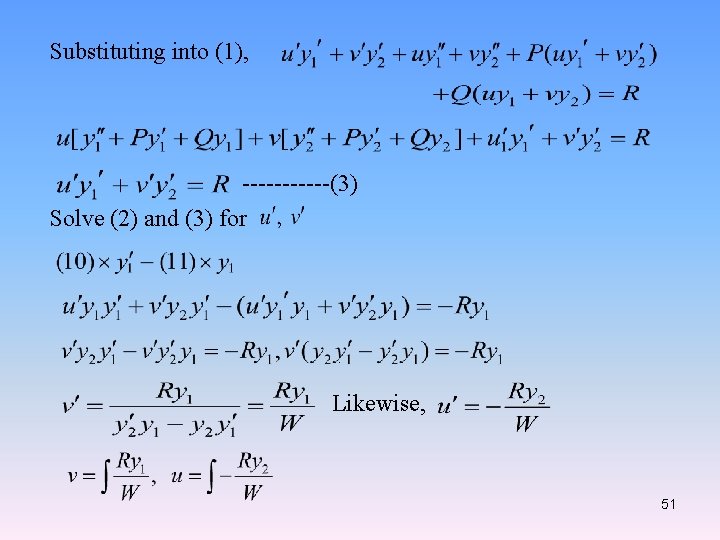
Substituting into (1), ------(3) Solve (2) and (3) for . Likewise, 51

。 Example : ------(A) i) General homogeneous solution : Let. Substitute into (A) The characteristic equation: Complex solutions: Real solutions: : independent 52
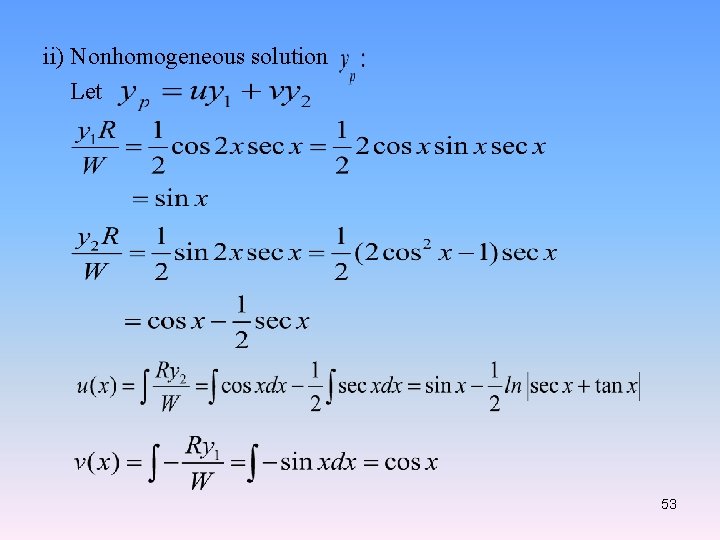
ii) Nonhomogeneous solution Let 53
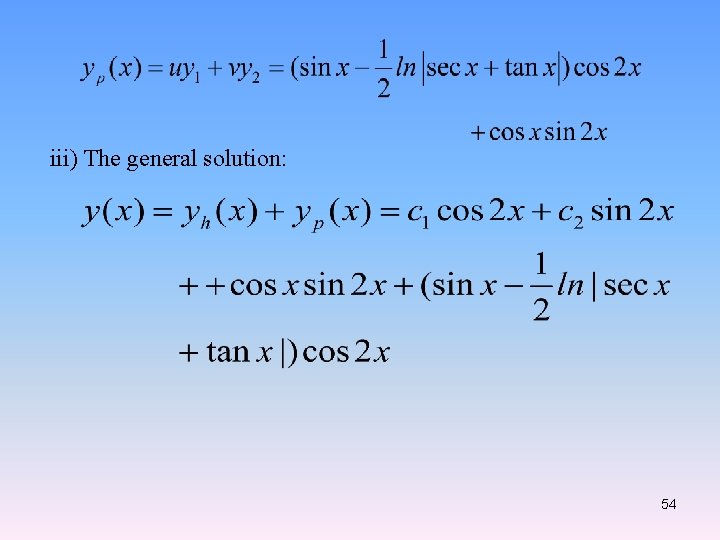
iii) The general solution: 54