18 SECONDORDER DIFFERENTIAL EQUATIONS SECONDORDER DIFFERENTIAL EQUATIONS 18


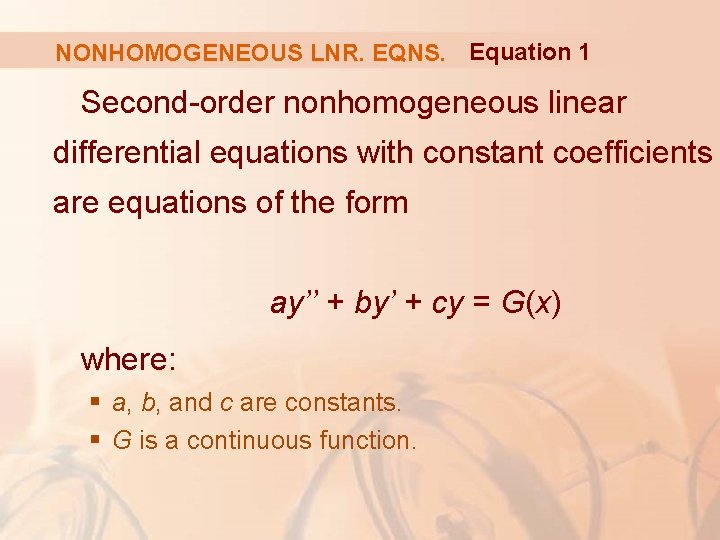









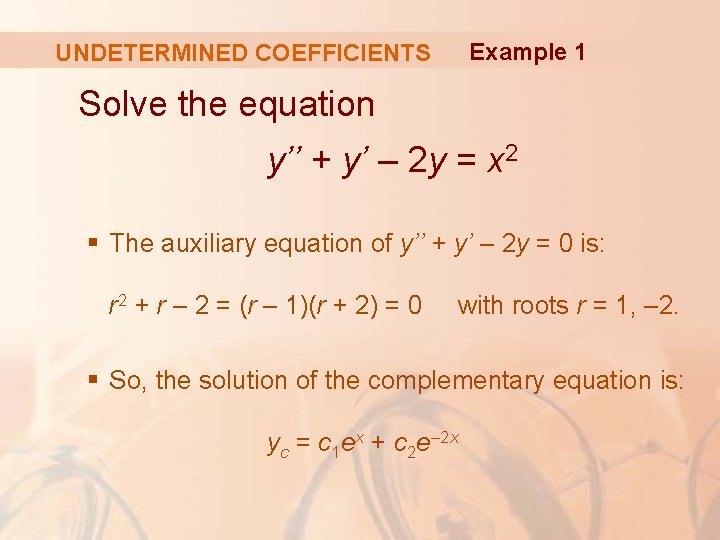





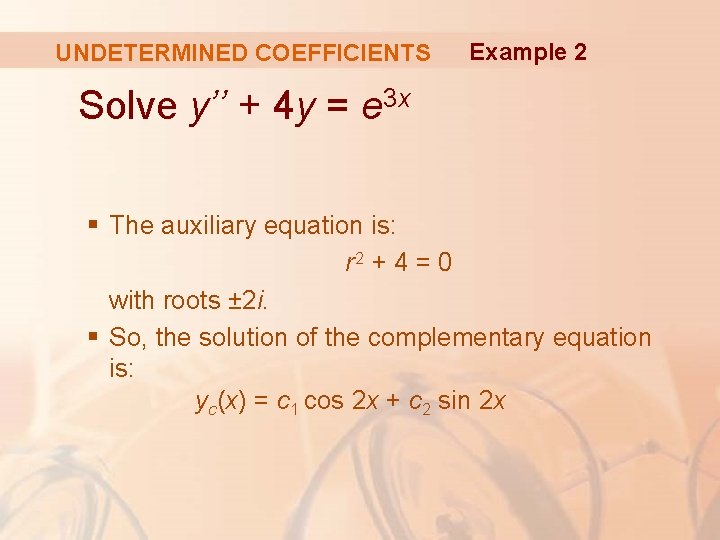




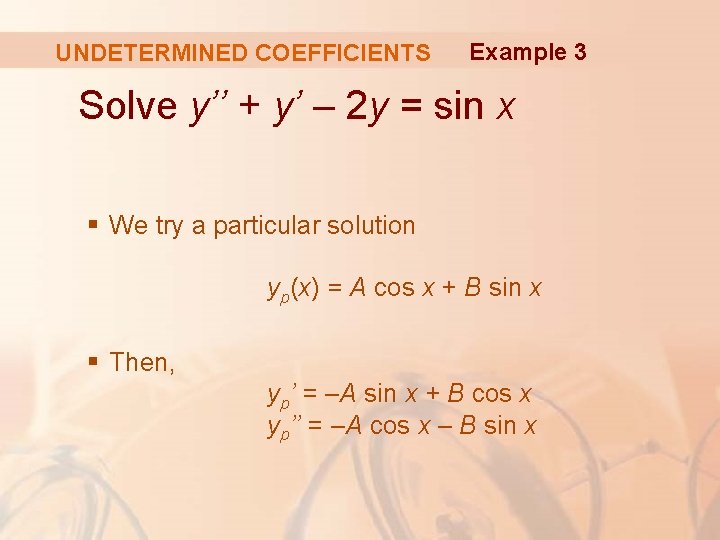





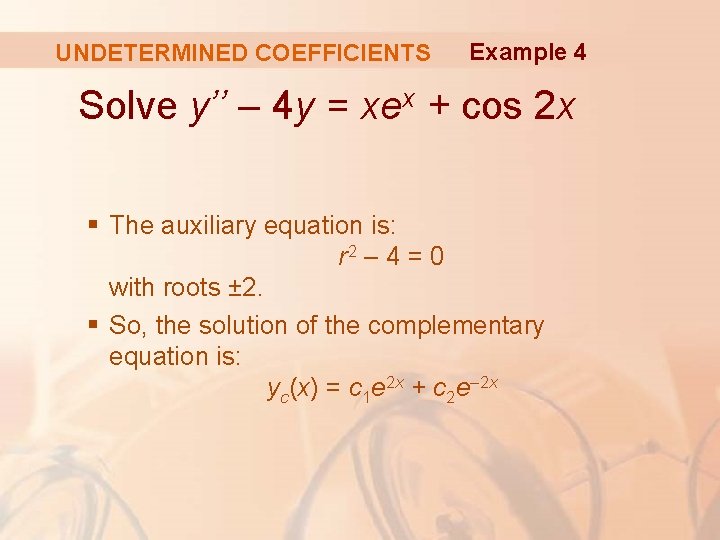



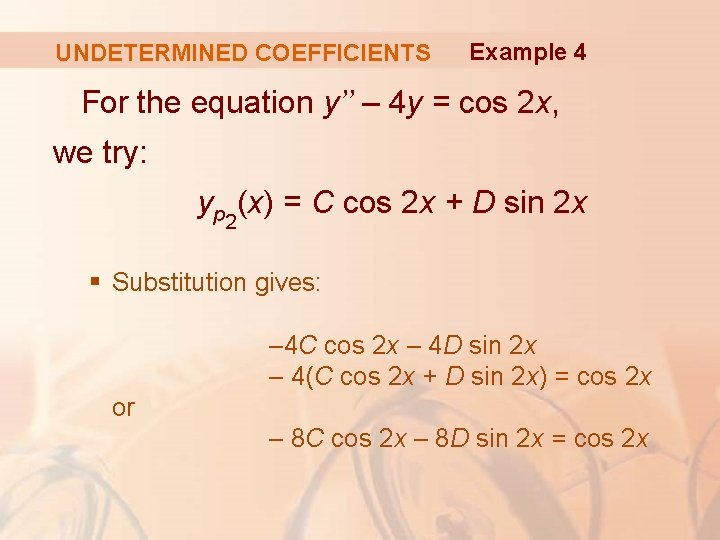


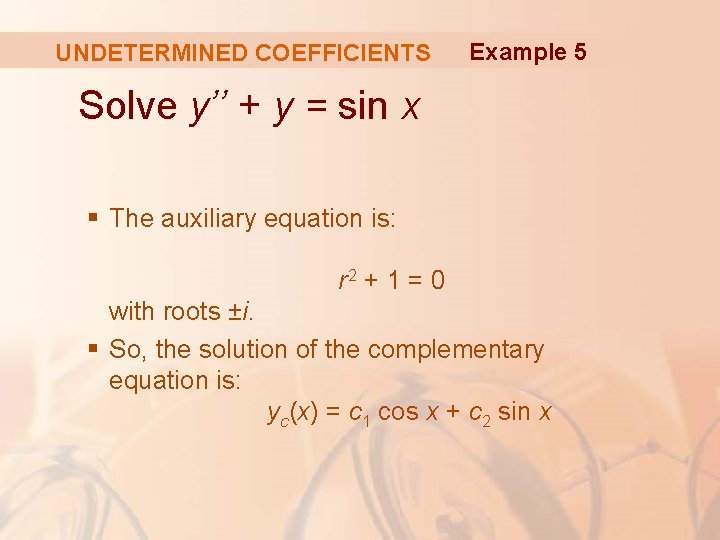































- Slides: 73

18 SECOND-ORDER DIFFERENTIAL EQUATIONS

SECOND-ORDER DIFFERENTIAL EQUATIONS 18. 2 Nonhomogeneous Linear Equations In this section, we will learn how to solve: Second-order nonhomogeneous linear differential equations with constant coefficients.
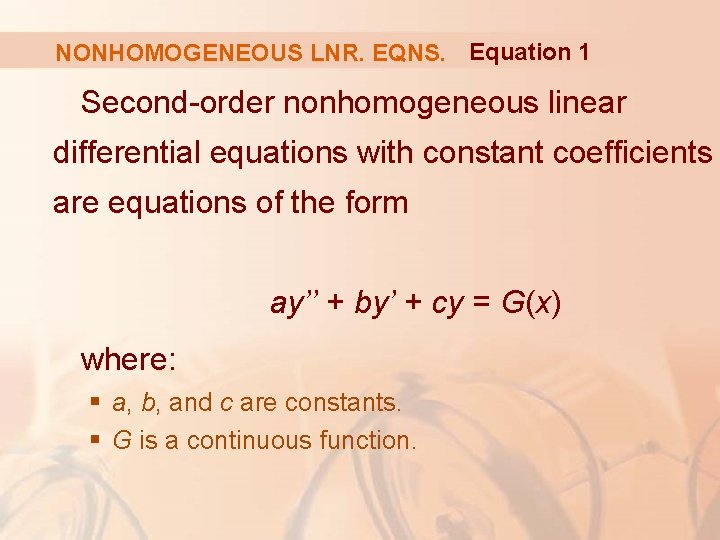
NONHOMOGENEOUS LNR. EQNS. Equation 1 Second-order nonhomogeneous linear differential equations with constant coefficients are equations of the form ay’’ + by’ + cy = G(x) where: § a, b, and c are constants. § G is a continuous function.

COMPLEMENTARY EQUATION Equation 2 The related homogeneous equation ay’’ + by’ + cy = 0 is called the complementary equation. § It plays an important role in the solution of the original nonhomogeneous equation 1.

NONHOMOGENEOUS LNR. EQNS. Theorem 3 The general solution of the nonhomogeneous differential equation 1 can be written as y(x) = yp(x) + yc(x) where: § yp is a particular solution of Equation 1. § yc is the general solution of Equation 2.

NONHOMOGENEOUS LNR. EQNS. Proof All we have to do is verify that, if y is any solution of Equation 1, then y – yp is a solution of the complementary Equation 2. § Indeed, a(y – yp)’’ + b(y – yp)’ + c(y – yp) = ay’’ – ayp’’ + by’ – byp’ + cy – cyp = (ay’’ + by’ + cy) – (ayp’’ + byp’ + cyp) = g(x) – g(x) =0

NONHOMOGENEOUS LNR. EQNS. We know from Section 17. 1 how to solve the complementary equation. § Recall that the solution is: yc = c 1 y 1 + c 2 y 2 where y 1 and y 2 are linearly independent solutions of Equation 2.

NONHOMOGENEOUS LNR. EQNS. Thus, Theorem 3 says that: § We know the general solution of the nonhomogeneous equation as soon as we know a particular solution yp.

METHODS TO FIND PARTICULAR SOLUTION There are two methods for finding a particular solution: § The method of undetermined coefficients is straightforward, but works only for a restricted class of functions G. § The method of variation of parameters works for every function G, but is usually more difficult to apply in practice.

UNDETERMINED COEFFICIENTS We first illustrate the method of undetermined coefficients for the equation ay’’ + by’ + cy = G(x) where G(x) is a polynomial.

UNDETERMINED COEFFICIENTS It is reasonable to guess that there is a particular solution yp that is a polynomial of the same degree as G: § If y is a polynomial, then ay’’ + by’ + cy is also a polynomial.

UNDETERMINED COEFFICIENTS Thus, we substitute yp(x) = a polynomial (of the same degree as G) into the differential equation and determine the coefficients.
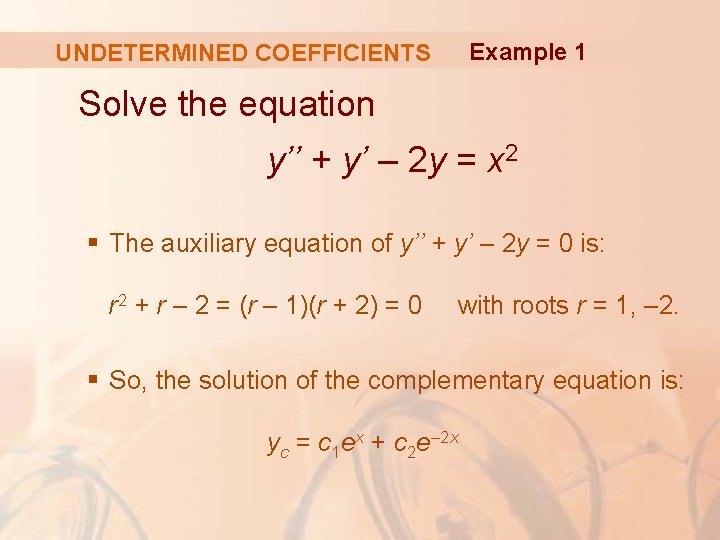
UNDETERMINED COEFFICIENTS Example 1 Solve the equation y’’ + y’ – 2 y = x 2 § The auxiliary equation of y’’ + y’ – 2 y = 0 is: r 2 + r – 2 = (r – 1)(r + 2) = 0 with roots r = 1, – 2. § So, the solution of the complementary equation is: yc = c 1 ex + c 2 e– 2 x

UNDETERMINED COEFFICIENTS Example 1 Since G(x) = x 2 is a polynomial of degree 2, we seek a particular solution of the form yp(x) = Ax 2 + Bx + C Then, § yp’ = 2 Ax + B § yp’’ = 2 A

UNDETERMINED COEFFICIENTS Example 1 So, substituting into the given differential equation, we have: (2 A) + (2 Ax + B) – 2(Ax 2 + Bx + C) = x 2 or – 2 Ax 2 + (2 A – 2 B)x + (2 A + B – 2 C) = x 2

UNDETERMINED COEFFICIENTS Example 1 Polynomials are equal when their coefficients are equal. Thus, – 2 A = 1 2 A – 2 B = 0 2 A + B – 2 C = 0 § The solution of this system of equations is: A = –½ B = –½ C = –¾

UNDETERMINED COEFFICIENTS Example 1 A particular solution, therefore, is: yp(x) = –½x 2 –½x – ¾ By Theorem 3, the general solution is: y = yc + yp = c 1 ex + c 2 e-2 x – ½x 2 – ½x – ¾

UNDETERMINED COEFFICIENTS Suppose G(x) (right side of Equation 1) is of the form Cekx, where C and k are constants. Then, we take as a trial solution a function of the same form, yp(x) = Aekx. § This is because the derivatives of ekx are constant multiples of ekx.

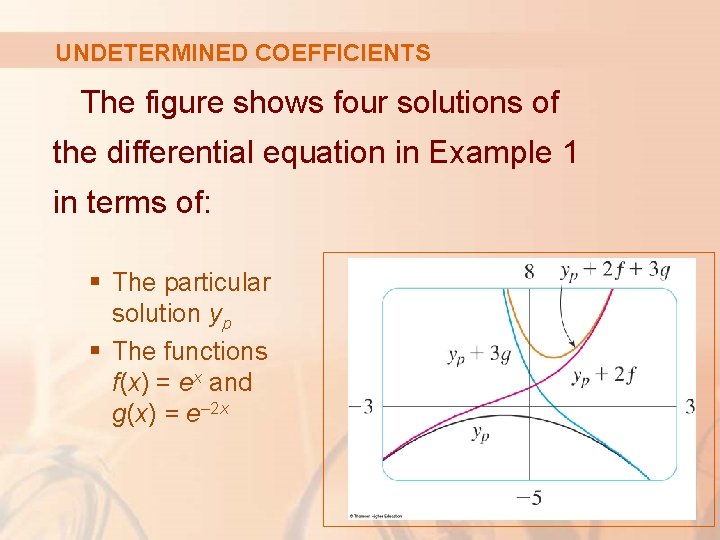
UNDETERMINED COEFFICIENTS The figure shows four solutions of the differential equation in Example 1 in terms of: § The particular solution yp § The functions f(x) = ex and g(x) = e– 2 x
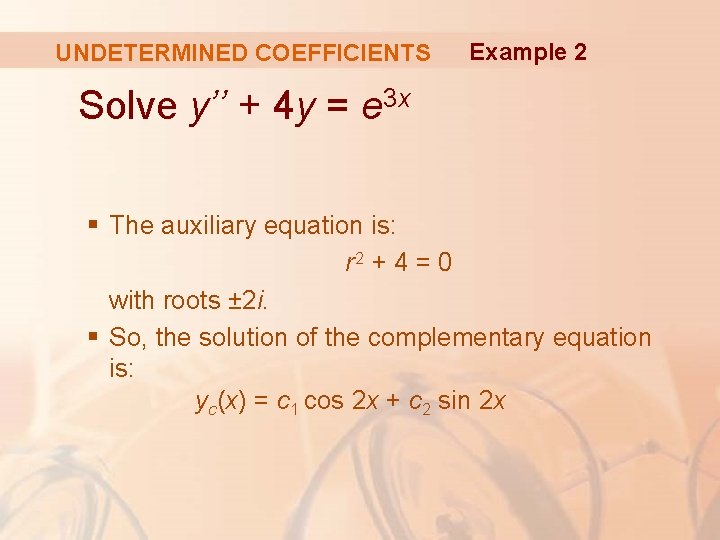
UNDETERMINED COEFFICIENTS Example 2 Solve y’’ + 4 y = e 3 x § The auxiliary equation is: r 2 + 4 = 0 with roots ± 2 i. § So, the solution of the complementary equation is: yc(x) = c 1 cos 2 x + c 2 sin 2 x

UNDETERMINED COEFFICIENTS Example 2 For a particular solution, we try: yp(x) = Ae 3 x Then, § yp’ = 3 Ae 3 x § yp’’ = 9 Ae 3 x

UNDETERMINED COEFFICIENTS Example 2 Substituting into the differential equation, we have: 9 Ae 3 x + 4(Ae 3 x) = e 3 x § So, and 13 Ae 3 x = e 3 x A = 1/13

UNDETERMINED COEFFICIENTS Example 2 Thus, a particular solution is: yp(x) = 1/13 e 3 x The general solution is: y(x) = c 1 cos 2 x + c 2 sin 2 x + 1/13 e 3 x

UNDETERMINED COEFFICIENTS Suppose G(x) is either C cos kx or C sin kx. § Then, because of the rules for differentiating the sine and cosine functions, we take as a trial particular solution a function of the form yp(x) = A cos kx + B sin kx

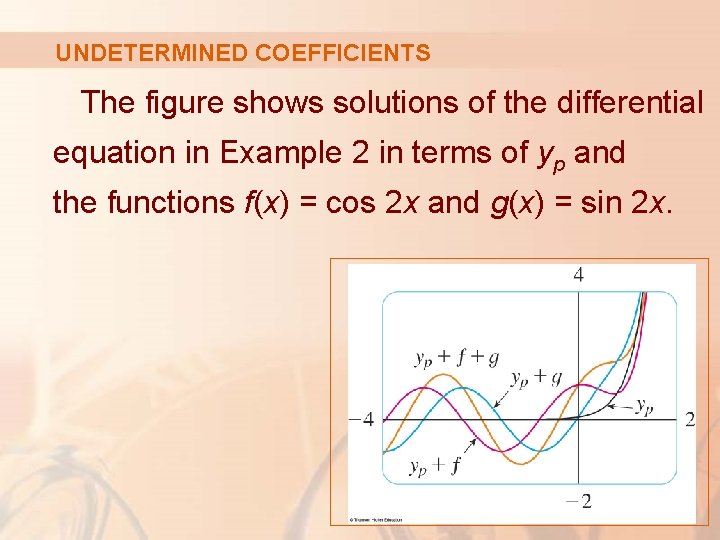
UNDETERMINED COEFFICIENTS The figure shows solutions of the differential equation in Example 2 in terms of yp and the functions f(x) = cos 2 x and g(x) = sin 2 x.

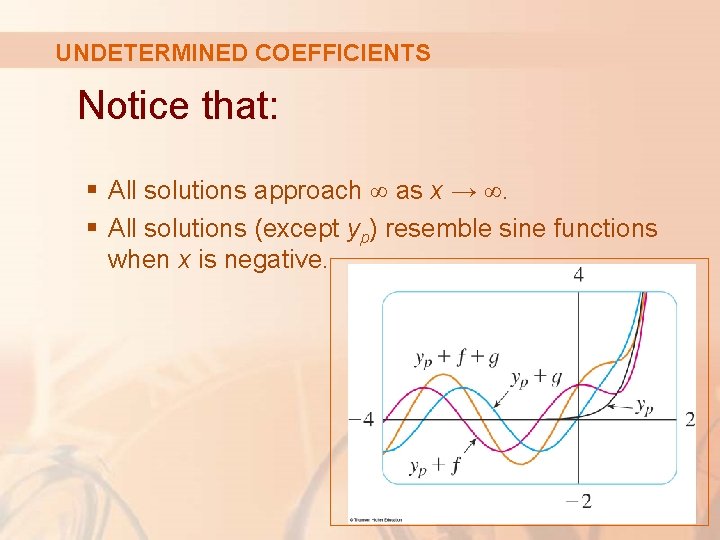
UNDETERMINED COEFFICIENTS Notice that: § All solutions approach ∞ as x → ∞. § All solutions (except yp) resemble sine functions when x is negative.
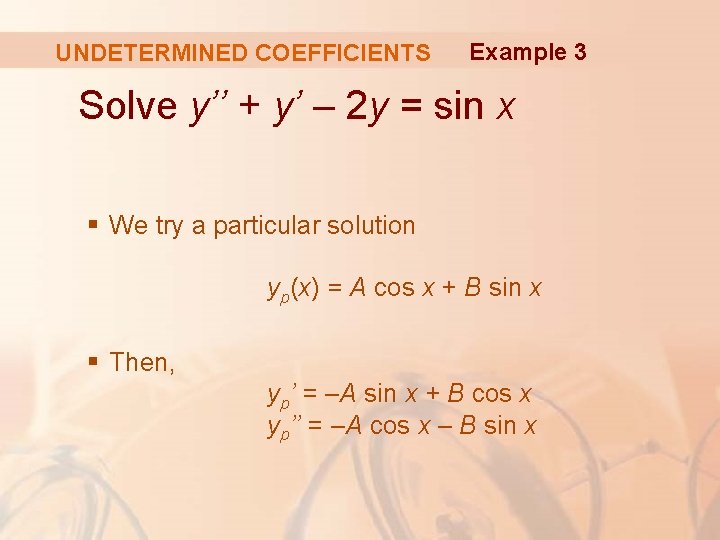
UNDETERMINED COEFFICIENTS Example 3 Solve y’’ + y’ – 2 y = sin x § We try a particular solution yp(x) = A cos x + B sin x § Then, yp’ = –A sin x + B cos x yp’’ = –A cos x – B sin x

UNDETERMINED COEFFICIENTS Example 3 So, substitution in the differential equation gives: (–A cos x – B sin x) + (–A sin x + B cos x) – 2(A cos x + B sin x) = sin x or (– 3 A + B) cos x + (–A – 3 B) sin x = sin x

UNDETERMINED COEFFICIENTS Example 3 This is true if: – 3 A + B = 0 and –A – 3 B = 1 § The solution of this system is: A = – 1/10 B = – 3/10 § So, a particular solution is: yp(x) = – 1/10 cos x – 3/10 sin x

UNDETERMINED COEFFICIENTS Example 3 In Example 1, we determined that the solution of the complementary equation is: yc = c 1 ex + c 2 e– 2 x § So, the general solution of the given equation is: y(x) = c 1 ex + c 2 e– 2 x – 1/10 (cos x – 3 sin x)

UNDETERMINED COEFFICIENTS If G(x) is a product of functions of the preceding types, we take the trial solution to be a product of functions of the same type. § For instance, in solving the differential equation y’’ + 2 y’ + 4 y = x cos 3 x we could try yp(x) = (Ax + B) cos 3 x + (Cx + D) sin 3 x

UNDETERMINED COEFFICIENTS If G(x) is a sum of functions of these types, we use the principle of superposition, which says that: § If yp 1 and yp 2 are solutions of ay’’ + by’ + cy = G 1(x) ay’’ + by’ + cy = G 2(x) respectively, then yp 1 + yp 2 is a solution of ay’’ + by’ + cy = G 1(x) + G 2(x)
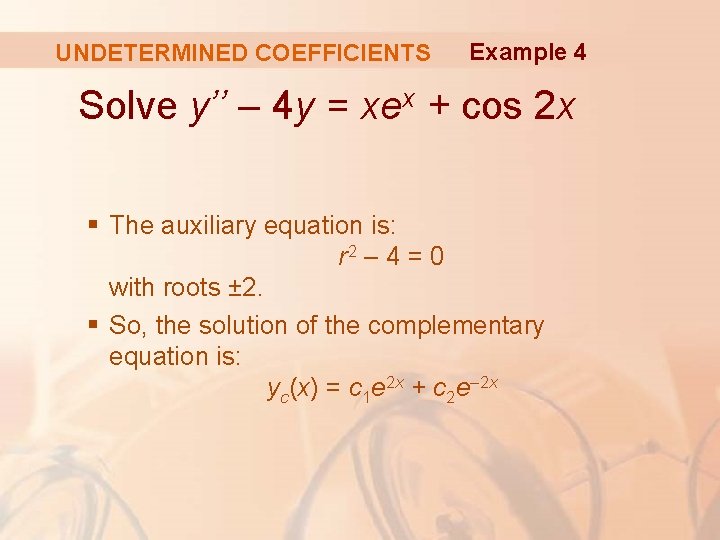
UNDETERMINED COEFFICIENTS Example 4 Solve y’’ – 4 y = xex + cos 2 x § The auxiliary equation is: r 2 – 4 = 0 with roots ± 2. § So, the solution of the complementary equation is: yc(x) = c 1 e 2 x + c 2 e– 2 x

UNDETERMINED COEFFICIENTS Example 4 For the equation y’’ – 4 y = xex, we try: yp 1(x) = (Ax + B)ex Then, § y’p 1= (Ax + A + B)ex § y’’p 1= (Ax + 2 A + B)ex

UNDETERMINED COEFFICIENTS Example 4 So, substitution in the equation gives: (Ax + 2 A + B)ex – 4(Ax + B)ex = xex or (– 3 Ax + 2 A – 3 B)ex = xex

UNDETERMINED COEFFICIENTS Example 4 Thus, – 3 A = 1 and 2 A – 3 B = 0 § So, A = –⅓, B = – 2/9, and yp 1(x) = (–⅓x – 2/9)ex
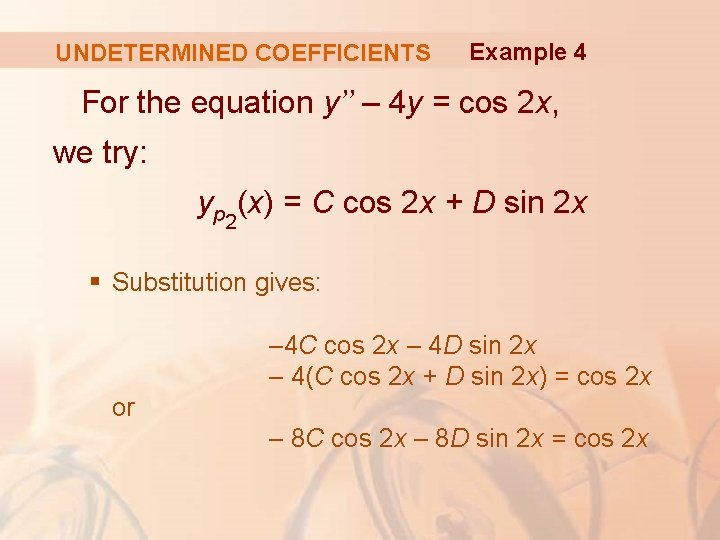
UNDETERMINED COEFFICIENTS Example 4 For the equation y’’ – 4 y = cos 2 x, we try: yp 2(x) = C cos 2 x + D sin 2 x § Substitution gives: – 4 C cos 2 x – 4 D sin 2 x – 4(C cos 2 x + D sin 2 x) = cos 2 x or – 8 C cos 2 x – 8 D sin 2 x = cos 2 x

UNDETERMINED COEFFICIENTS Example 4 Thus, – 8 C = 1, – 8 D = 0, and yp 2(x) = – 1/8 cos 2 x § By the superposition principle, the general solution is: y = yc + yp 1 + yp 2 = c 1 e 2 x + c 2 e-2 x – (1/3 x + 2/9)ex – 1/8 cos 2 x

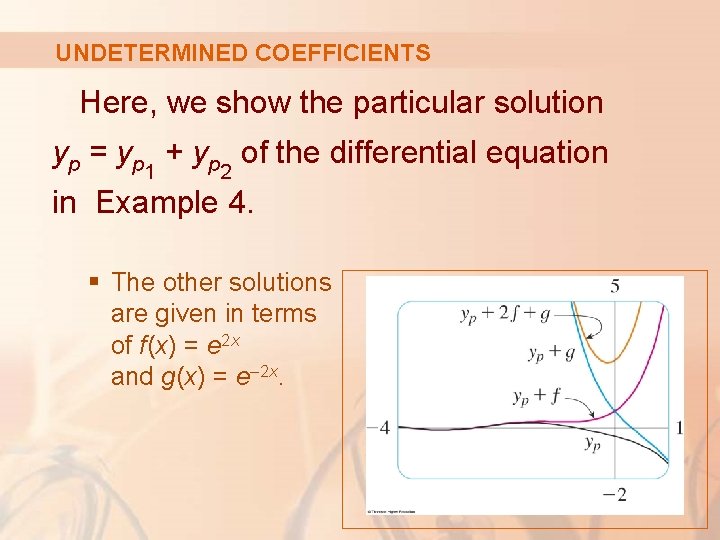
UNDETERMINED COEFFICIENTS Here, we show the particular solution yp = yp 1 + yp 2 of the differential equation in Example 4. § The other solutions are given in terms of f(x) = e 2 x and g(x) = e– 2 x.

UNDETERMINED COEFFICIENTS Finally, we note that the recommended trial solution yp sometimes turns out to be a solution of the complementary equation. § So, it can’t be a solution of the nonhomogeneous equation. § In such cases, we multiply the recommended trial solution by x (or by x 2 if necessary) so that no term in yp(x) is a solution of the complementary equation.
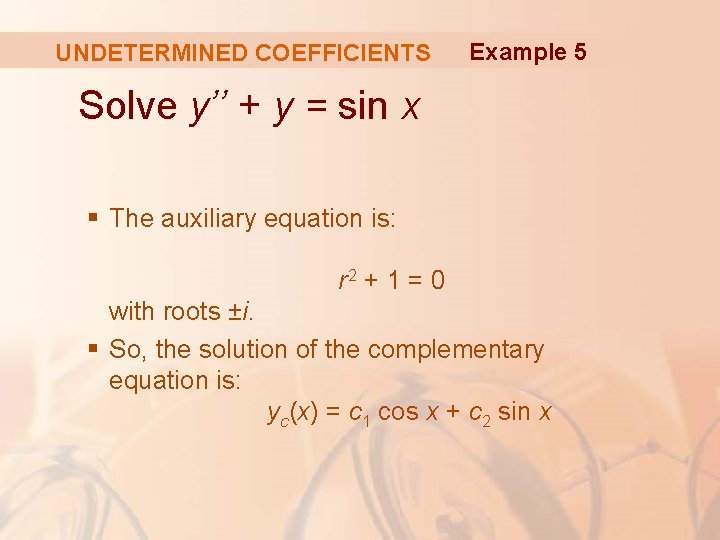
UNDETERMINED COEFFICIENTS Example 5 Solve y’’ + y = sin x § The auxiliary equation is: r 2 + 1 = 0 with roots ±i. § So, the solution of the complementary equation is: yc(x) = c 1 cos x + c 2 sin x

UNDETERMINED COEFFICIENTS Example 5 Ordinarily, we would use the trial solution yp(x) = A cos x + B sin x § However, we observe that it is a solution of the complementary equation. § So, instead, we try: yp(x) = Ax cos x + Bx sin x

UNDETERMINED COEFFICIENTS Example 5 Then, § yp’(x) = A cos x – Ax sin x + Bx cos x § yp’’(x) = – 2 A sin x – Ax cos x + 2 B cos x – Bx sin x

UNDETERMINED COEFFICIENTS Example 5 Substitution in the differential equation gives: yp’’ + yp = – 2 A sin x + 2 B cos x = sin x § So, A = –½ , B = 0, and yp(x) = –½x cos x § The general solution is: y(x) = c 1 cos x + c 2 sin x – ½ x cos x

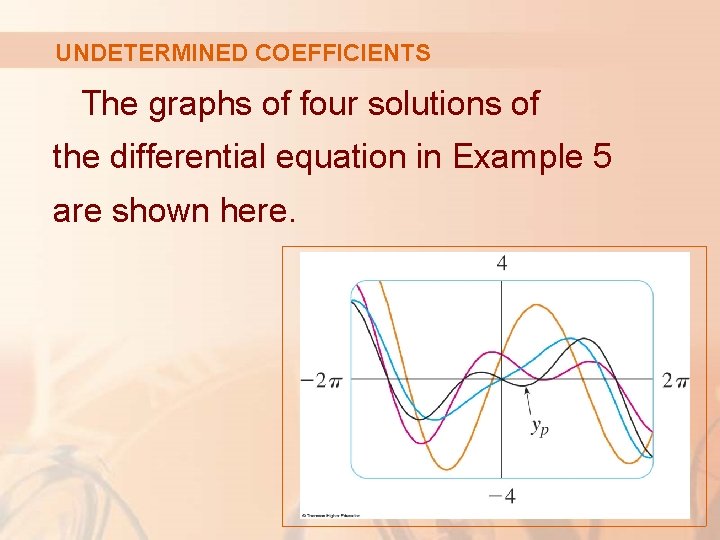
UNDETERMINED COEFFICIENTS The graphs of four solutions of the differential equation in Example 5 are shown here.

UNDETERMINED COEFFICIENTS We summarize the method of undetermined coefficients as follows.

SUMMARY—PART 1 If G(x) = ekx. P(x), where P is a polynomial of degree n, then try: yp(x) = ekx. Q(x) where Q(x) is an nth-degree polynomial (whose coefficients are determined by substituting in the differential equation).

SUMMARY—PART 2 If G(x) = ekx. P(x)cos mx or G(x) = ekx. P(x) sin mx where P is an nth-degree polynomial, then try: yp(x) = ekx. Q(x) cos mx + ekx. R(x) sin mx where Q and R are nth-degree polynomials.

SUMMARY—MODIFICATION If any term of yp is a solution of the complementary equation, multiply yp by x (or by x 2 if necessary).

UNDETERMINED COEFFICIENTS Example 6 Determine the form of the trial solution for the differential equation y’’ – 4 y’ + 13 y = e 2 x cos 3 x

UNDETERMINED COEFFICIENTS Example 6 G(x) has the form of part 2 of the summary, where k = 2, m = 3, and P(x) = 1. § So, at first glance, the form of the trial solution would be: yp(x) = e 2 x(A cos 3 x + B sin 3 x)

UNDETERMINED COEFFICIENTS Example 6 However, the auxiliary equation is: r 2 – 4 r + 13 = 0 with roots r = 2 ± 3 i. § So, the solution of the complementary equation is: yc(x) = e 2 x(c 1 cos 3 x + c 2 sin 3 x)

UNDETERMINED COEFFICIENTS Example 6 This means that we have to multiply the suggested trial solution by x. § So, instead, we use: yp(x) = xe 2 x(A cos 3 x + B sin 3 x)

VARIATION OF PARAMETERS Equation 4 Suppose we have already solved the homogeneous equation ay’’ + by’ + cy = 0 and written the solution as: y(x) = c 1 y 1(x) + c 2 y 2(x) where y 1 and y 2 are linearly independent solutions.

VARIATION OF PARAMETERS Let’s replace the constants (or parameters) c 1 and c 2 in Equation 4 by arbitrary functions u 1(x) and u 2(x).

VARIATION OF PARAMETERS Equation 5 We look for a particular solution of the nonhomogeneous equation ay’’ + by’ + cy = G(x) of the form yp(x) = u 1(x) y 1(x) + u 2(x) y 2(x)

VARIATION OF PARAMETERS This method is called variation of parameters because we have varied the parameters c 1 and c 2 to make them functions.

VARIATION OF PARAMETERS Equation 6 Differentiating Equation 5, we get: yp’ = (u 1’y 1 + u 2’y 2) + (u 1 y 1’ + u 2 y 2’)

VARIATION OF PARAMETERS Since u 1 and u 2 are arbitrary functions, we can impose two conditions on them. § One condition is that yp is a solution of the differential equation. § We can choose the other condition so as to simplify our calculations.

VARIATION OF PARAMETERS Equation 7 In view of the expression in Equation 6, let’s impose the condition that: u 1’y 1 + u 2’y 2 = 0 § Then, yp’’ = u 1’y 1’ + u 2’y 2’ + u 1 y 1’’ + u 2 y 2’’

VARIATION OF PARAMETERS Equation 8 Substituting in the differential equation, we get: a(u 1’y 1’ + u 2’y 2’ + u 1 y 1’’ + u 2 y 2’’) + b(u 1 y 1’ + u 2 y 2’) + c(u 1 y 1 + u 2 y 2) = G or u 1(ay 1” + by 1’ + cy 1) + u 2(ay 2” + by 2” + cy 2) + a(u 1’y 1’ + u 2’y 2’) = G

VARIATION OF PARAMETERS However, y 1 and y 2 are solutions of the complementary equation. So, ay 1’’ + by 1’ + cy 1 = 0 and ay 2’’ + by 2’ + cy 2 = 0

VARIATION OF PARAMETERS Equation 9 Thus, Equation 8 simplifies to: a(u 1’y 1’ + u 2’y 2’) = G

VARIATION OF PARAMETERS Equations 7 and 9 form a system of two equations in the unknown functions u 1’ and u 2’. § After solving this system, we may be able to integrate to find u 1 and u 2. § Then, the particular solution is given by Equation 5.

VARIATION OF PARAMETERS Example 7 Solve the equation y’’ + y = tan x, 0 < x < π/2 § The auxiliary equation is: r 2 + 1 = 0 with roots ±i. § So, the solution of y’’ + y = 0 is: c 1 sin x + c 2 cos x

VARIATION OF PARAMETERS Example 7 Using variation of parameters, we seek a solution of the form yp(x) = u 1(x) sin x + u 2(x) cos x § Then, yp’ = (u 1’ sin x + u 2’ cos x) + (u 1 cos x – u 2 sin x)

VARIATION OF PARAMETERS E. g. 7—Equation 10 Set u 1’ sin x + u 2’ cos x = 0 § Then, yp’’ = u 1’ cos x – u 2’ sin x – u 1 sin x – u 2 cos x

VARIATION OF PARAMETERS E. g. 7—Equation 11 For yp to be a solution, we must have: yp’’ + yp = u 1’ cos x – u 2’ sin x = tan x

VARIATION OF PARAMETERS Example 7 Solving Equations 10 and 11, we get: u 1’(sin 2 x + cos 2 x) = cos x tan x u 1’ = sin x u 1(x) = –cos x § We seek a particular solution. § So, we don’t need a constant of integration here.

VARIATION OF PARAMETERS Then, from Equation 10, we obtain: Example 7

VARIATION OF PARAMETERS Example 7 So, u 2(x) = sin x – ln(sec x + tan x) § Note that: sec x + tan x > 0 for 0 < x < π/2

VARIATION OF PARAMETERS Example 7 Therefore, yp(x) = –cos x sin x + [sin x – ln(sec x + tan x)] cos x = –cos x ln(sec x + tan x) § The general solution is: y(x) = c 1 sin x + c 2 cos x – cos x ln(sec x + tan x)

VARIATION OF PARAMETERS The figure shows four solutions of the differential equation in Example 7.
 Logistic growth equation biology
Logistic growth equation biology Integration of partial differential equation
Integration of partial differential equation Find the general solution of the differential equation
Find the general solution of the differential equation Stewart differential equations
Stewart differential equations Munthe sizing
Munthe sizing Cengage differential equations
Cengage differential equations Variable separable
Variable separable How to solve second order differential equations
How to solve second order differential equations Partial differential equations
Partial differential equations Derivation of maxwell's equations in differential form
Derivation of maxwell's equations in differential form Natural solution
Natural solution Annihilator method
Annihilator method Bernoulli equation differential equations examples
Bernoulli equation differential equations examples Partial differential equation
Partial differential equation 1st order derivative formula
1st order derivative formula Differential equations projects
Differential equations projects Differential equations formula
Differential equations formula Higher order linear differential equations
Higher order linear differential equations First ode
First ode Differential equations chapter 1
Differential equations chapter 1 Slidetodoc
Slidetodoc Non linear ode
Non linear ode What is a first order equation
What is a first order equation Differential equations summary
Differential equations summary Differential equations with discontinuous forcing functions
Differential equations with discontinuous forcing functions Ordinary differential equations example
Ordinary differential equations example Growth and decay differential equation
Growth and decay differential equation Parachute problem
Parachute problem Integrating factor of differential equation
Integrating factor of differential equation Euler method formula
Euler method formula Ppt on differential equations
Ppt on differential equations Hcc differential equations
Hcc differential equations Independent variable definition
Independent variable definition First ode
First ode Hertz
Hertz Differential equations
Differential equations Euler midpoint method
Euler midpoint method Definition and classification of differential equations
Definition and classification of differential equations Ordinary differential equation
Ordinary differential equation Non linear ode
Non linear ode Method of characteristics
Method of characteristics Differential equations zill solutions
Differential equations zill solutions Definition of homogeneous differential equation
Definition of homogeneous differential equation Pde paula
Pde paula First-order differential equations
First-order differential equations Numerical methods for partial differential equations eth
Numerical methods for partial differential equations eth Derivation of maxwell's equations in differential form
Derivation of maxwell's equations in differential form Mixing problems differential equations
Mixing problems differential equations Separation of variables differential equations
Separation of variables differential equations Mechanical and electrical vibrations differential equations
Mechanical and electrical vibrations differential equations Differential equations with discontinuous forcing functions
Differential equations with discontinuous forcing functions Calculus equations
Calculus equations Traffic flow differential equations
Traffic flow differential equations Polar and rectangular forms of equations
Polar and rectangular forms of equations Translating chemical equations
Translating chemical equations Classification scale
Classification scale Saw tooth appearance in lichen planus
Saw tooth appearance in lichen planus Dc analysis of differential amplifier
Dc analysis of differential amplifier Educadora differential amplifier
Educadora differential amplifier Eisenmenger syndrome
Eisenmenger syndrome Differential thermal analysis
Differential thermal analysis H165 differential amplifier
H165 differential amplifier Antrectomy
Antrectomy Linear variable differential transformer
Linear variable differential transformer Dd jaundice
Dd jaundice Linear differential equation formula
Linear differential equation formula Differential calculus formulas
Differential calculus formulas Broad differential meaning
Broad differential meaning Impossible differential equation
Impossible differential equation Semantic differential scale
Semantic differential scale Dda computer graphics
Dda computer graphics Differential levelling
Differential levelling General purpose media
General purpose media Differential low-cost access to productive inputs
Differential low-cost access to productive inputs