Second order differential equations Introduction Second order differential

















































- Slides: 60

Second order differential equations

Introduction • Second order differential equations allow you to solve a variety of problems in economics, physics and engineering • Examples include modelling shock absorption and variation of current in an electrical circuit • These methods were originally created by Leonhard Euler and Jean le Rond d’Alambert

Teachings for Exercise 5 A

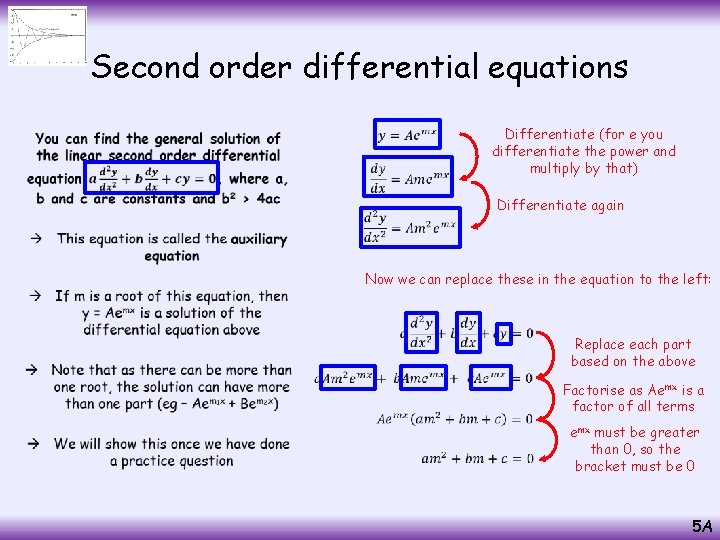
Second order differential equations • Divide all by a Divide all by y Subtract b/a Multiply by dx (now the variables are separated) Integrate each side Calculate the Integrals, using ln. A to represent the constant Exponentials of each side You can think of the powers of e as a multiplication eln. A = A as they cancel out 5 A

Second order differential equations • As the solution to the first order differential equation looks like this, it implies that the second order differential will take a similar form (because we would essentially solve it in a similar way) 5 A

Second order differential equations Differentiate (for e you differentiate the power and multiply by that) • Differentiate again Now we can replace these in the equation to the left: Replace each part based on the above Factorise as Aemx is a factor of all terms emx must be greater than 0, so the bracket must be 0 5 A

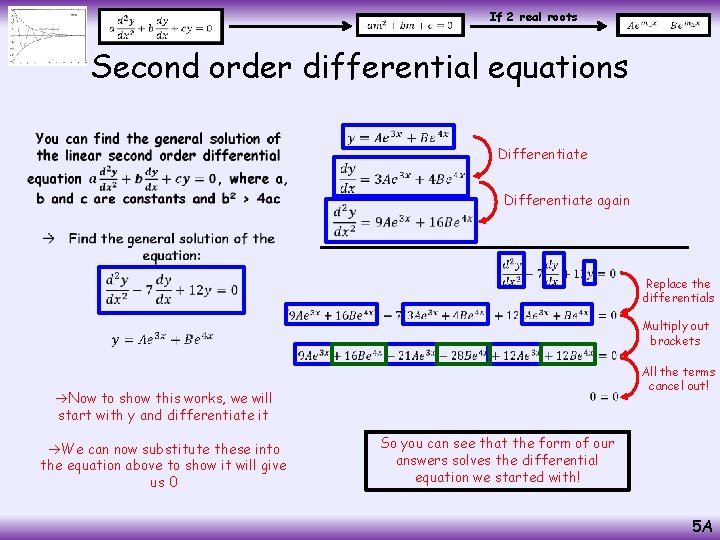
If 2 real roots Second order differential equations • Form the auxiliary equation Factorise it Solve Now we can substitute the roots into the form above At this point we do not have enough information to work out the values of A and B (they are equivalent to the +C you get when integrating!) m 1 = 3 and m 2 = 4 5 A

If 2 real roots Second order differential equations • Differentiate again Now to show this works, we will start with y and differentiate it We can now substitute these into the equation above to show it will give us 0 Replace the differentials Multiply out brackets All the terms cancel out! So you can see that the form of our answers solves the differential equation we started with! 5 A

Teachings for Exercise 5 B

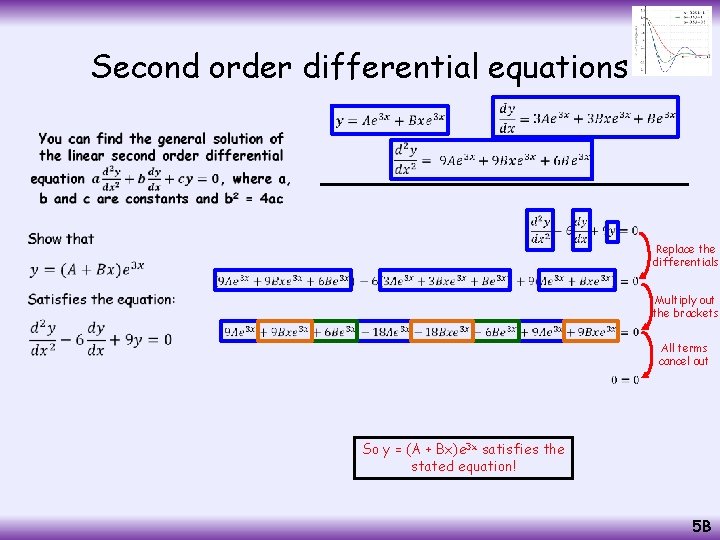
Second order differential equations • Multiply out the bracket Differentiate – the second term needs the product rule… Differentiate again, using the product rule where needed Simplify 3 x Product rule for 3 Bxe 3 x 5 B

Second order differential equations • Replace the differentials Multiply out the brackets All terms cancel out So y = (A + Bx)e 3 x satisfies the stated equation! 5 B

If repeated roots Second order differential equations • Form the auxiliary equation Factorise Solve Now we can substitute the root into the form above: m = -4 5 B

Teachings for Exercise 5 C

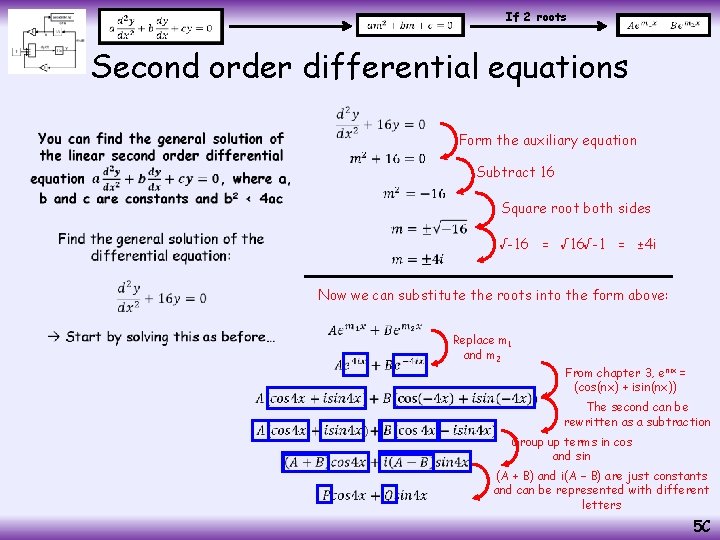
If 2 roots Second order differential equations • Form the auxiliary equation Subtract 16 Square root both sides √-16 = √ 16√-1 = ± 4 i Now we can substitute the roots into the form above: Replace m 1 and m 2 From chapter 3, enix = (cos(nx) + isin(nx)) The second can be rewritten as a subtraction Group up terms in cos and sin (A + B) and i(A – B) are just constants and can be represented with different letters 5 C

If 2 roots Second order differential equations • 5 C

If 2 roots Second order differential equations • Form the auxiliary equation Factorise (or use the quadratic formula) Completing the square is often effective in these questions! Group terms Subtract 25 Square root Add 3 5 C

If 2 roots Second order differential equations Now we can substitute the roots into the form above: • Sub in the two solutions m 1 and m 2 Think of the powers of e as a multiplication Factorise as e 3 x is common to both The part in the bracket can be rewritten as you have just seen So if the root is of the form: The solution will be of the form: 5 C

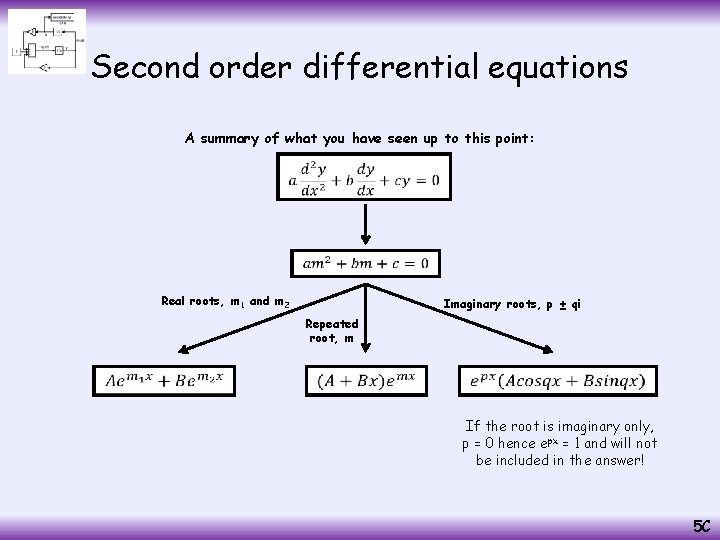
Second order differential equations A summary of what you have seen up to this point: Real roots, m 1 and m 2 Imaginary roots, p ± qi Repeated root, m If the root is imaginary only, p = 0 hence epx = 1 and will not be included in the answer! 5 C

Teachings for Exercise 5 D

Second order differential equations • However, to solve an equation which is equal to a function of x, you also need to calculate the Particular Integral and add it on You will need to do this for these possible forms of f(x) We will have a look at dealing with each of these types now! 5 D

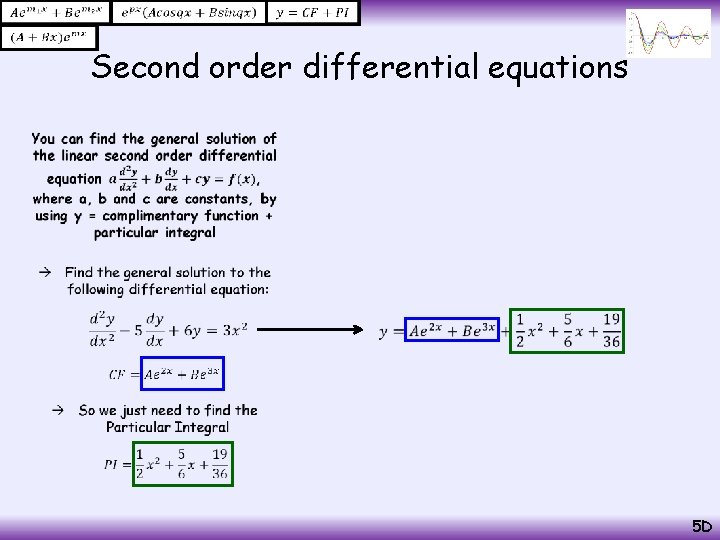
Second order differential equations Complimentary Function • Form the auxiliary equation Factorise Solve Sub the two answers into the ‘real roots’ form above m 1 = 2 and m 2 = 3 This is the complimentary function (sometimes abbreviated as ‘CF’) 5 D

Second order differential equations We let y = λ as it is the same form as f(x) λ represents a constant value (a number) • Particular Integral Now differentiate this expression for y Differentiate again You can substitute these into the differential equation The differentials are equal to 0 so they will be cancelled Solve for λ So the Particular Integral (PI) is equal to 1/2 5 D

Second order differential equations • Replace CF and PI with the expressions we found We will now check that this works… 5 D

Second order differential equations • Differentiate again Substitute these into the differential equation Replace the differentials Expand brackets All terms cancel except the 3! So you can see that the process has worked! 5 D

Second order differential equations • 5 D

Second order differential equations • We let y = λx + μ as it is the same form as f(x) λ and μ represent constant values Particular Integral Now differentiate this expression for y Differentiate again You can substitute these into the differential equation The second differential will be cancelled out Multiply out the bracket 5 D

Second order differential equations • We let y = λx + μ as it is the same form as f(x) λ and μ represent constant values Compare coefficients of x on each side – they must be equal… Divide by 6 Compare coefficients of the ‘constant’ on each side – they must be equal as well… Sub in the value of λ that we have found Particular Integral Solve for μ We now know the value of the Particular Integral! 5 D

Second order differential equations We let y = λx 2 + μx + v as it is the same form as f(x) • Particular Integral λ, μ and v represent constant values Now differentiate this expression for y Differentiate again You can substitute these into the differential equation Sub in differentials Multiply out the brackets Group terms in x 2, x and constants separately 5 D

Second order differential equations • We let y = λx 2 + μx + v as it is the same form as f(x) λ, μ and v represent constant values Compare coefficients of x 2 Solve Compare coefficients of x Particular Integral Use the value of λ to help solve Compare constants Use the values of λ and μ to help solve 5 D

Second order differential equations • 5 D

Second order differential equations • We let y = λex as it is the same form as f(x) λ represents a constant value Particular Integral Now differentiate this expression for y Differentiate again You can substitute these into the differential equation Replace the differentials Simplify Find the value of λ 5 D

Second order differential equations • Particular Integral We let y = λsinx + µcosx as it is the same form as f(x) (you need both sin AND cos!) λ and µ represent constant values Now differentiate this expression for y Differentiate again You can substitute these into the differential equation Replace the differentials Multiply out the brackets Group terms in sin and cos 5 D

Second order differential equations We let y = λsinx + µcosx as it is the same form as f(x) (you need both sin AND cos!) • λ and µ represent constant values Compare coefficients of sin 3 x Compare coefficients of cos 3 x You can solve these equations simultaneously Multiply by 5 Add together Particular Integral Solve Use to find µ 5 D

Second order differential equations Complimentary Function • Form the auxiliary equation Factorise Solve Sub the two answers into the ‘real roots’ form above m 1 = 0 and m 2 = 2 e 0 x = 1 5 D

Second order differential equations Particular Integral • Normally, we would now let y = λ However, if you look at the complimentary function, we already have a term of this form, ‘A’. Therefore, the Particular Integral cannot be of this form as it has already been absorbed into the CF In situations like this, we can introduce ‘x’ into the equation with λ in Now differentiate this expression for y Differentiate again Now substitute these into the equation to find λ Replace the differentials – the second one cancels Find the value of λ 5 D

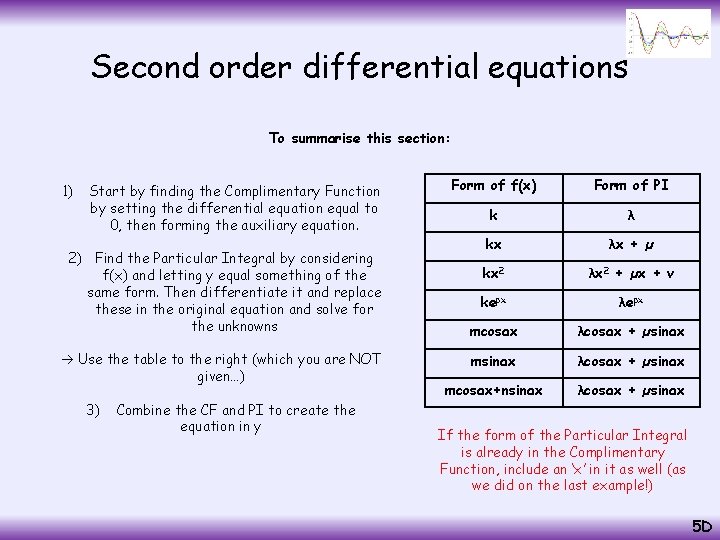
Second order differential equations To summarise this section: 1) Start by finding the Complimentary Function by setting the differential equation equal to 0, then forming the auxiliary equation. 2) Find the Particular Integral by considering f(x) and letting y equal something of the same form. Then differentiate it and replace these in the original equation and solve for the unknowns Use the table to the right (which you are NOT given…) 3) Combine the CF and PI to create the equation in y Form of f(x) Form of PI k λ kx λx + µ kx 2 λx 2 + µx + v kepx λepx mcosax λcosax + µsinax msinax λcosax + µsinax mcosax+nsinax λcosax + µsinax If the form of the Particular Integral is already in the Complimentary Function, include an ‘x’ in it as well (as we did on the last example!) 5 D

Teachings for Exercise 5 E

Second order differential equations • 5 E

Second order differential equations Complimentary Function • Form the auxiliary equation Square root Sub the two answers into the ‘real roots’ form above Add 1 m 1 = 1 and m 2 = -1 5 E

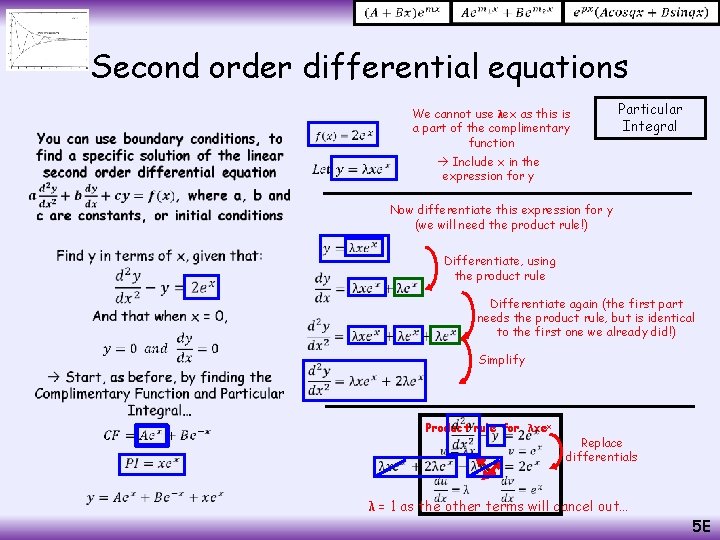
Second order differential equations • We cannot use λex as this is a part of the complimentary function Include x in the expression for y Particular Integral Now differentiate this expression for y (we will need the product rule!) Differentiate, using the product rule Differentiate again (the first part needs the product rule, but is identical to the first one we already did!) Simplify rule for λxex Product Replace differentials λ = 1 as the other terms will cancel out… 5 E

Second order differential equations • When x = 0, y = 0 Calculate Differentiate (using the product rule for xex) When x = 0, dy/ dx =0 Calculate Rearrange 5 E

Second order differential equations • Add together Solve Use this to find B Now we have A and B, we finally have the solution of the differential equation, given the conditions we were told! 5 E

Second order differential equations Complimentary Function • Form the auxiliary equation Subtract 1 Square root Sub the two answers into the ‘imaginary roots’ form above (remember as there is no real part, we can ignore the part outside the bracket…) q = 1 (as it is ± 1 i) Also, remember that for this example we are using t, not x here! 5 E

Second order differential equations • Remember to use x in place of y, and t in place of x Differentiate again Replace the differentials Simplify Particular Integral Use the form you’re given! Calculate λ 5 E

Second order differential equations • When t = 0, x=0 Calculate As we found the value of A straight away, we can update the equation for x… (This is an important step as it can make the next step, differentiation, much easier) Differentiate When t = 0, Update, with A = 0 and B = 3 =1 Calculate dx/ dt Add 2 5 E

Teachings for Exercise 5 F

Second order differential equations You can use a given substitution to transform a second order differential equation into one of the previous types of equation, which you can then solve You saw this type of process in Chapter 4 – where a equation which doesn’t fit the ‘pattern’ we need can be modified by a substitution You will almost certainly be given the substitution to use in these questions 5 F

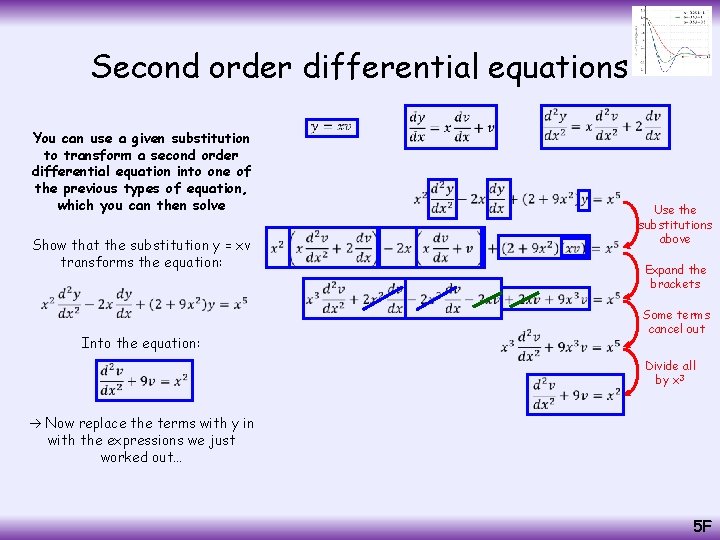
Second order differential equations You can use a given substitution to transform a second order differential equation into one of the previous types of equation, which you can then solve Show that the substitution y = xv transforms the equation: Use the substitution you are given to find the differentials Differentiate using the product rule Simplify Into the equation: Productrulefor forxdv xv Product /dx Differentiate with respect to x You need to replace all the terms with y in, including the differentials… Differentiate using the product rule for the first part (I have used ‘a’ and ‘b’ to avoid confusion with the ‘v’ term that is already in there!) 5 F

Second order differential equations You can use a given substitution to transform a second order differential equation into one of the previous types of equation, which you can then solve Show that the substitution y = xv transforms the equation: Use the substitutions above Expand the brackets Into the equation: Some terms cancel out Divide all by x 3 Now replace the terms with y in with the expressions we just worked out… 5 F

Second order differential equations Complimentary Function You can use a given substitution to transform a second order differential equation into one of the previous types of equation, which you can then solve Form the auxiliary equation Subtract 9 Show that the substitution y = xv transforms the equation: Square root Sub the two answers into the ’imaginary roots’ form above (remember as there is no real part, we can ignore the part outside the bracket…) Into the equation: q = 3 (as it is ± 3 i) Now we have to find the solution to this equation as we have seen before 5 F

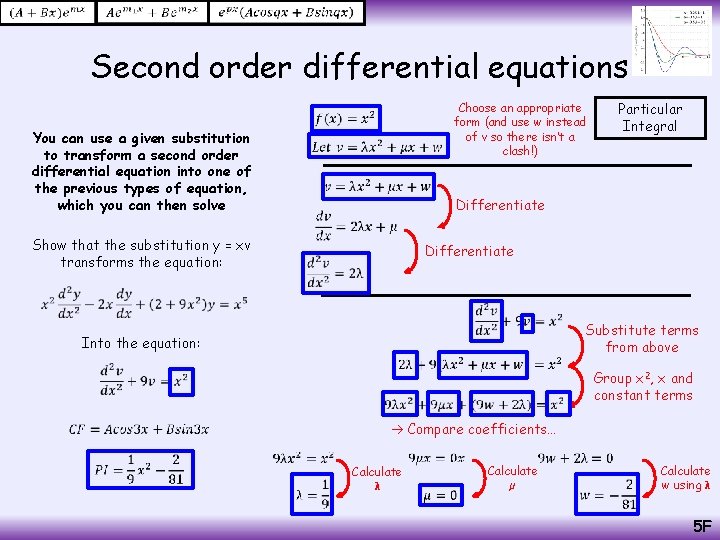
Second order differential equations Choose an appropriate form (and use w instead of v so there isn’t a clash!) You can use a given substitution to transform a second order differential equation into one of the previous types of equation, which you can then solve Differentiate Show that the substitution y = xv transforms the equation: Differentiate Substitute terms from above Into the equation: Group x 2, x and constant terms Compare coefficients… Particular Integral Calculate λ Calculate µ Calculate w using λ 5 F

Second order differential equations You can use a given substitution to transform a second order differential equation into one of the previous types of equation, which you can then solve We need to use the original substitution to bring y back into the equation… Show that the substitution y = xv transforms the equation: Divide by x Replace v with the expression in y and x Into the equation: Multiply by x Expand the bracket (or leave as it is!) 5 F

Second order differential equations You can use a given substitution to transform a second order differential equation into one of the previous types of equation, which you can then solve Given that: Find the general solution of the equation: This question initially looks similar to the previous one, but it is actually very different… You have been given x in terms of u This means you have to replace the x terms with u terms As a result, you need to change dy/dx terms into dy/du terms (so you are changing the denominator rather than the numerator, as in the previous example) In addition, your substitution does not even have y in it, so how on earth can you get dy/dx in the first place? You will need to use the chain rule in this type of question! 5 F

Second order differential equations You can use a given substitution to transform a second order differential equation into one of the previous types of equation, which you can then solve Start by differentiating the equation you’re using for substitution… Differentiate Given that: Now you can use the Chain rule to involve dy/du and dy/dx so they can be replaced. You will need to include dx/du as well Find the general solution of the equation: This is usually easier if you start with ’du/dx =‘ rather than ’dy/dx =‘ This question initially looks similar to the previous one, but it is actually very different… Now we need to continue this process to find an expression for the other differential Replace dx/du with the expression we worked out Replace eu with x (from above) This is very useful as this gives us an exact expression we want to replace! 5 F

Second order differential equations You can use a given substitution to transform a second order differential equation into one of the previous types of equation, which you can then solve Given that: Differentiate using the product rule, with respect to u dx/ du Find the general solution of the equation: This question initially looks similar to the previous one, but it is actually very different… Replace x with eu We will differentiate with respect to u in a moment and it is easier if the parts are in terms of u (we can’t do anything with the dy/dx though!) = x and eu = x as well Replace xdy/dx with Subtract dy/ du Again, this is very useful as this is the exact expression we want to replace! dy/ du u (I will explain the differentiation of dy/dx with respect to u on the next slide…) 5 F

Second order differential equations You can use a given substitution to transform a second order differential equation into one of the previous types of equation, which you can then solve Given that: Differentiating When there isn’t a ‘y’ on the top, it doesn’t really change much. It just means you’re differentiating the function in the bracket after it… Find the general solution of the equation: dy/ dx with respect to u Replace the first differential using the chain rule dy/ dx of dy/dx gives a second differential Just change the order This question initially looks similar to the previous one, but it is actually very different… You can think of d/du as being effectively the same as Therefore, by the chain rule: dy/ du 5 F

Second order differential equations You can use a given substitution to transform a second order differential equation into one of the previous types of equation, which you can then solve We can use these to remove the x terms in the function! Replace the differentials Given that: Find the general solution of the equation: This question initially looks similar to the previous one, but it is actually very different… Simplify Now we can start solving this as before, by finding the Complimentary Function and Particular Integral! Although in this particular example, we do not need the Particular Integral as the equation is set equal to 0 5 F

Second order differential equations You can use a given substitution to transform a second order differential equation into one of the previous types of equation, which you can then solve Find the general solution of the equation: Form the auxiliary equation Subtract 1 Given that: Complimentary Function Square root Sub the two answers into the ’imaginary roots’ form above (remember as there is no real part, we can ignore the part outside the bracket…) Also, REMEMBER TO USE u, NOT x!!! This question initially looks similar to the previous one, but it is actually very different… q = 1 (as it is ± 1 i) 5 F

Second order differential equations You can use a given substitution to transform a second order differential equation into one of the previous types of equation, which you can then solve Finally, we now need to replace u in terms of x Given that: Simplify Find the general solution of the equation: Take natural logarithms Use this to replace u This question initially looks similar to the previous one, but it is actually very different… You will probably need quite a lot of practice at this type of question – there are many different substitutions you might be asked to use! 5 F

Summary • You have learnt how to solve second order differential equations • You have seen that the answer will have different forms depending on the nature of the roots • You have also seen how to use information to calculate the unknowns • You have used substitutions to change the equations into ones that are simpler to solve
 How to solve second order differential equations
How to solve second order differential equations Linear partial differential equations examples
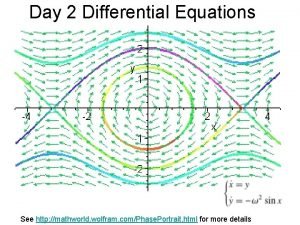
Linear partial differential equations examples Wolfram alpha phase portrait
Wolfram alpha phase portrait Symlicity
Symlicity Differential equation pendulum
Differential equation pendulum How to solve linear first order differential equations
How to solve linear first order differential equations Find the general solution of the differential equation
Find the general solution of the differential equation First order ode
First order ode Solving 1st order differential equations
Solving 1st order differential equations 1st order derivative formula
1st order derivative formula Example of ordinary differential equation
Example of ordinary differential equation First order linear equation
First order linear equation First order linear equation
First order linear equation Higher order linear differential equations
Higher order linear differential equations Second order change
Second order change First order cybernetics and second order cybernetics
First order cybernetics and second order cybernetics Via optica
Via optica Differential equations projects
Differential equations projects Exact differential equation ppt
Exact differential equation ppt Paul heckbert
Paul heckbert Cengage differential equations
Cengage differential equations Euler midpoint method
Euler midpoint method Differential calculus
Differential calculus Differential equations definition
Differential equations definition Seperation of variables
Seperation of variables Cengage differential equations
Cengage differential equations Natural solution
Natural solution Definition and classification of differential equations
Definition and classification of differential equations Traffic flow differential equations
Traffic flow differential equations Runge kutta second order method formula
Runge kutta second order method formula Slidetodoc.com
Slidetodoc.com Differential equations
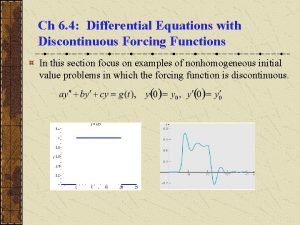
Differential equations Differential equations with discontinuous forcing functions
Differential equations with discontinuous forcing functions Bernoulli differential equation definition
Bernoulli differential equation definition Parachute problem differential equations
Parachute problem differential equations Non homogeneous differential equation
Non homogeneous differential equation Munthe sizing
Munthe sizing Exponential differential equation
Exponential differential equation Differential equations zill solutions
Differential equations zill solutions Stewart differential equations
Stewart differential equations Differential equations chapter 1
Differential equations chapter 1 Hertz
Hertz Mechanical and electrical vibrations
Mechanical and electrical vibrations Annihilator approach
Annihilator approach Ordinary differential equations example
Ordinary differential equations example Nonlinear ode
Nonlinear ode Integration of partial differential equation
Integration of partial differential equation Definition of differential equation
Definition of differential equation Mixing problems differential equations
Mixing problems differential equations Derivation of maxwell's equations in differential form
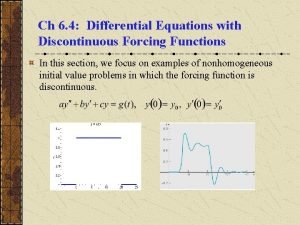
Derivation of maxwell's equations in differential form Differential equations with discontinuous forcing functions
Differential equations with discontinuous forcing functions Derivation of maxwell's equations in differential form
Derivation of maxwell's equations in differential form Partial differential equation solution
Partial differential equation solution Differential equations summary
Differential equations summary Piecewise differential equation
Piecewise differential equation Logistic growth curve equation
Logistic growth curve equation Differential equation for deflection
Differential equation for deflection Hcc differential equations
Hcc differential equations Numerical methods for partial differential equations eth
Numerical methods for partial differential equations eth 27 miles per gallon into kilometers per liter
27 miles per gallon into kilometers per liter Rectangular and polar coordinates
Rectangular and polar coordinates