The Promise of Differential Privacy Cynthia Dwork Microsoft





![Differential Privacy [D. , Mc. Sherry, Nissim, Smith 06] M gives (ε, 0) - Differential Privacy [D. , Mc. Sherry, Nissim, Smith 06] M gives (ε, 0) -](https://slidetodoc.com/presentation_image_h/236d3379f989b846665d32f0d8de133b/image-8.jpg)


![Vector-Valued Queries f = maxadj x, x’ ||f(x) – f(x’)||1 Theorem [DMNS 06]: On Vector-Valued Queries f = maxadj x, x’ ||f(x) – f(x’)||1 Theorem [DMNS 06]: On](https://slidetodoc.com/presentation_image_h/236d3379f989b846665d32f0d8de133b/image-15.jpg)


![Composition [D. , Rothblum, Vadhan’ 10] Composition [D. , Rothblum, Vadhan’ 10]](https://slidetodoc.com/presentation_image_h/236d3379f989b846665d32f0d8de133b/image-19.jpg)






![Algorithm and Privacy Analysis Caution: Conditional branch leaks private information! • [Hardt-Rothblum] Algorithm and Privacy Analysis Caution: Conditional branch leaks private information! • [Hardt-Rothblum]](https://slidetodoc.com/presentation_image_h/236d3379f989b846665d32f0d8de133b/image-28.jpg)





![Private Multiplicative Weights [Hardt-Rothblum’ 10] Represent database as (normalized) histogram on U Private Multiplicative Weights [Hardt-Rothblum’ 10] Represent database as (normalized) histogram on U](https://slidetodoc.com/presentation_image_h/236d3379f989b846665d32f0d8de133b/image-37.jpg)




![Boosting [Schapire, 1989] General method for improving accuracy of any given learning algorithm Example: Boosting [Schapire, 1989] General method for improving accuracy of any given learning algorithm Example:](https://slidetodoc.com/presentation_image_h/236d3379f989b846665d32f0d8de133b/image-44.jpg)


![Private Boosting for Queries [Variant of Ada. Boost] Initial distribution D is uniform on Private Boosting for Queries [Variant of Ada. Boost] Initial distribution D is uniform on](https://slidetodoc.com/presentation_image_h/236d3379f989b846665d32f0d8de133b/image-55.jpg)
![Private Boosting for Queries [Variant of Ada. Boost] Initial distribution D is uniform on Private Boosting for Queries [Variant of Ada. Boost] Initial distribution D is uniform on](https://slidetodoc.com/presentation_image_h/236d3379f989b846665d32f0d8de133b/image-56.jpg)







![High/Unknown Sensitivity Functions Subsample-and-Aggregate [Nissim, Raskhodnikova, Smith’ 07] High/Unknown Sensitivity Functions Subsample-and-Aggregate [Nissim, Raskhodnikova, Smith’ 07]](https://slidetodoc.com/presentation_image_h/236d3379f989b846665d32f0d8de133b/image-68.jpg)
![Functions “Expected” to Behave Well Propose-Test-Release [D. -Lei’ 09] Privacy-preserving test for “goodness” of Functions “Expected” to Behave Well Propose-Test-Release [D. -Lei’ 09] Privacy-preserving test for “goodness” of](https://slidetodoc.com/presentation_image_h/236d3379f989b846665d32f0d8de133b/image-69.jpg)

- Slides: 72

The Promise of Differential Privacy Cynthia Dwork, Microsoft Research

NOT A History Lesson Developments presented out of historical order; key results omitted

NOT Encyclopedic Whole sub-areas omitted

Outline Part 1: Basics Part 2: Many Queries Sparse Vector Multiplicative Weights Boosting for queries Part 3: Techniques Smoking causes cancer Definition Laplace mechanism Simple composition Histogram example Advanced composition Exponential mechanism and application Subsample-and-Aggregate Propose-Test-Release Application of S&A and PTR combined Future Directions

Basics Model, definition, one mechanism, two examples, composition theorem

Model for This Tutorial C Database is a collection of rows ? One person in the database Adversary/User and curator computationally unbounded All users are part of one giant adversary “Curator against the world”

Databases that Teach Database teaches that smoking causes cancer. Smoker S’s insurance premiums rise. This is true even if S not in database! Learning that smoking causes cancer is the whole point. Smoker S enrolls in a smoking cessation program. Differential privacy: limit harms to the teachings, not participation The outcome of any analysis is essentially equally likely, independent of whether any individual joins, or refrains from joining, the dataset. Automatically immune to linkage attacks
![Differential Privacy D Mc Sherry Nissim Smith 06 M gives ε 0 Differential Privacy [D. , Mc. Sherry, Nissim, Smith 06] M gives (ε, 0) -](https://slidetodoc.com/presentation_image_h/236d3379f989b846665d32f0d8de133b/image-8.jpg)
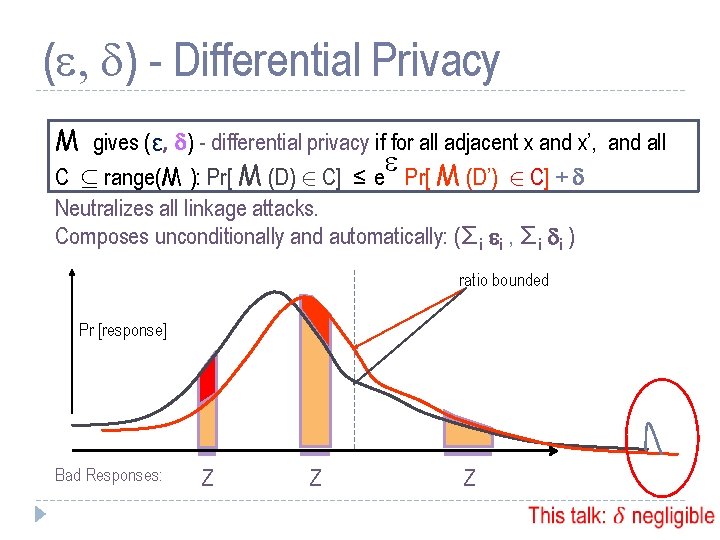
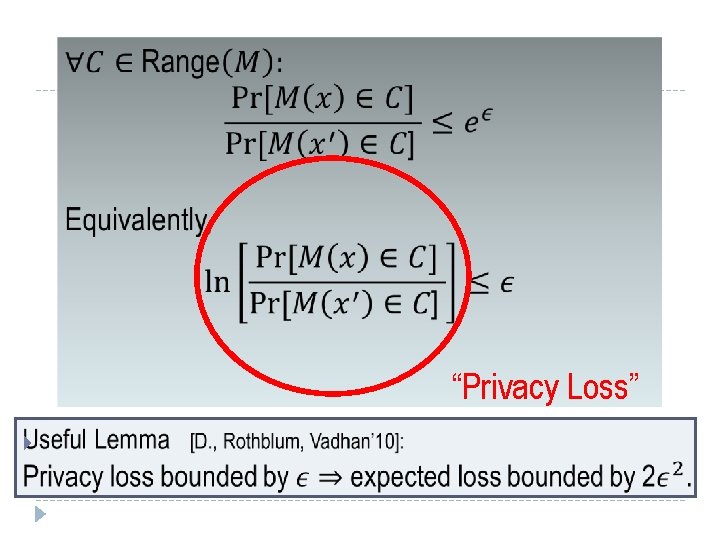
Differential Privacy [D. , Mc. Sherry, Nissim, Smith 06] M gives (ε, 0) - differential privacy if for all adjacent x and x’, and all C µ range(M): Pr[ M (x) 2 C] ≤ e Pr[ M (x’) 2 C] Neutralizes all linkage attacks. Composes unconditionally and automatically: Σi ε i ratio bounded Pr [response] Bad Responses: Z Z Z

( , d) - Differential Privacy M gives (ε, d) - differential privacy if for all adjacent x and x’, and all C µ range(M ): Pr[ M (D) 2 C] ≤ e Pr[ M (D’) 2 C] + d Neutralizes all linkage attacks. Composes unconditionally and automatically: (Σi i , Σi di ) ratio bounded Pr [response] Bad Responses: Z Z Z

“Privacy Loss”

Sensitivity of a Function f = maxadjacent x, x’ |f(x) – f(x’)| Adjacent databases differ in at most one row. Counting queries have sensitivity 1. Sensitivity captures how much one person’s data can affect output

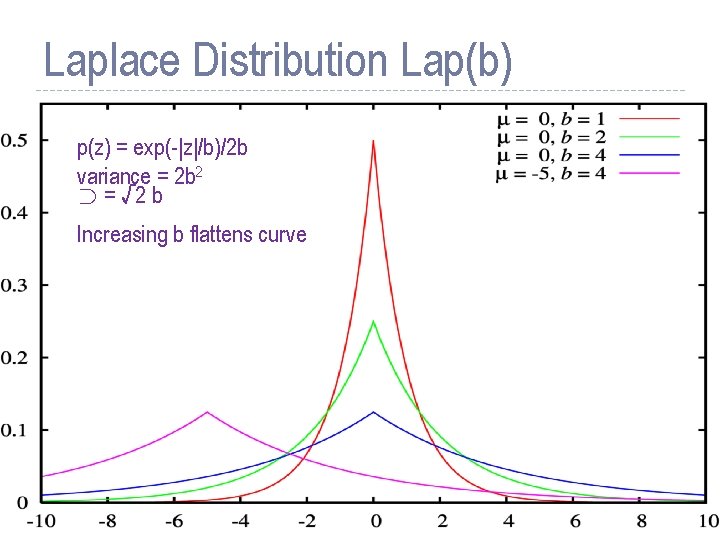
Laplace Distribution Lap(b) p(z) = exp(-|z|/b)/2 b variance = 2 b 2 ¾ = √ 2 b Increasing b flattens curve 13

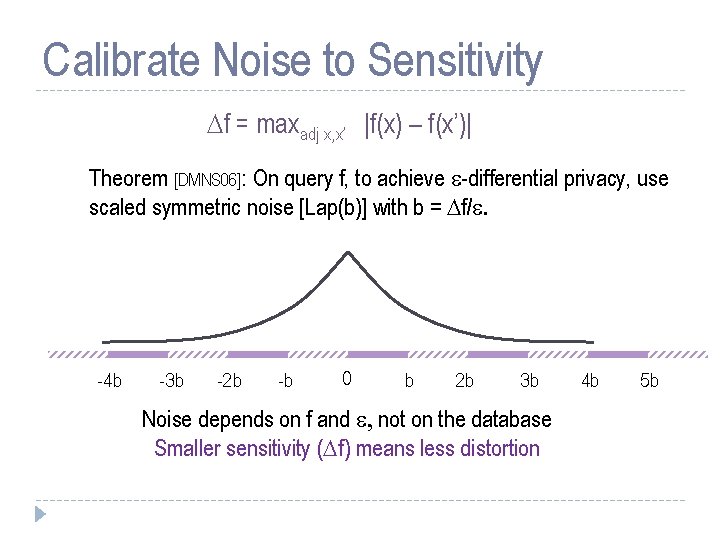
Calibrate Noise to Sensitivity f = maxadj x, x’ |f(x) – f(x’)| Theorem [DMNS 06]: On query f, to achieve -differential privacy, use scaled symmetric noise [Lap(b)] with b = f/. -4 b -3 b -2 b -b 0 b 2 b 3 b Noise depends on f and , not on the database Smaller sensitivity ( f) means less distortion 4 b 5 b

Example: Counting Queries
![VectorValued Queries f maxadj x x fx fx1 Theorem DMNS 06 On Vector-Valued Queries f = maxadj x, x’ ||f(x) – f(x’)||1 Theorem [DMNS 06]: On](https://slidetodoc.com/presentation_image_h/236d3379f989b846665d32f0d8de133b/image-15.jpg)
Vector-Valued Queries f = maxadj x, x’ ||f(x) – f(x’)||1 Theorem [DMNS 06]: On query f, to achieve -differential privacy, use scaled symmetric noise [Lap( f/ )]d. -4 b -3 b -2 b -b 0 b 2 b 3 b Noise depends on f and , not on the database Smaller sensitivity ( f) means less distortion 4 b 5 b

Example: Histograms f = maxadj x, x’ ||f(x) – f(x’)||1 Theorem: To achieve -differential privacy, use scaled symmetric noise [Lap( f/ )]d. 17

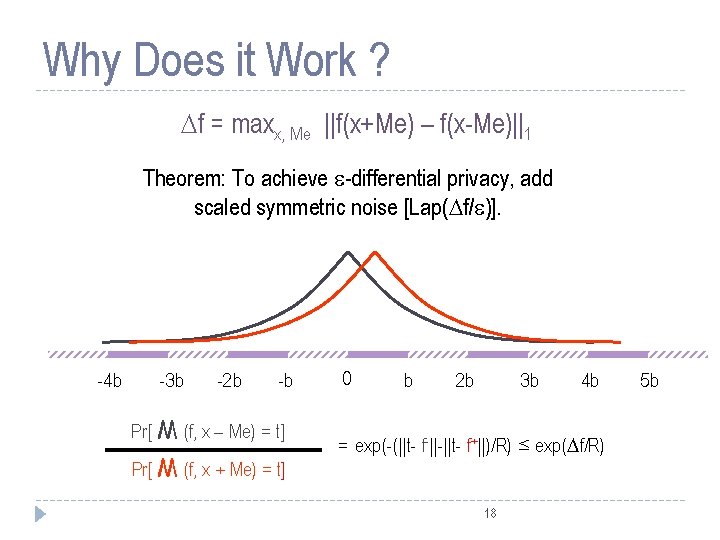
Why Does it Work ? f = maxx, Me ||f(x+Me) – f(x-Me)||1 Theorem: To achieve -differential privacy, add scaled symmetric noise [Lap( f/ )]. -4 b -3 b -2 b -b Pr[ M (f, x – Me) = t] Pr[ M (f, x + Me) = t] 0 b 2 b 3 b 4 b = exp(-(||t- f-||-||t- f+||)/R) ≤ exp( f/R) 18 5 b

“Simple” Composition k-fold composition of ( , ±)-differentially private mechanisms is (k , k±)-differentially private.
![Composition D Rothblum Vadhan 10 Composition [D. , Rothblum, Vadhan’ 10]](https://slidetodoc.com/presentation_image_h/236d3379f989b846665d32f0d8de133b/image-19.jpg)
Composition [D. , Rothblum, Vadhan’ 10]

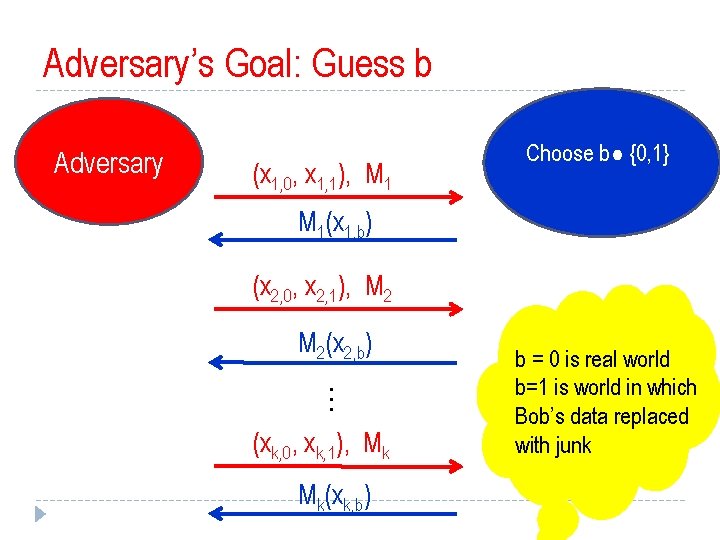
Adversary’s Goal: Guess b Adversary (x 1, 0, x 1, 1), M 1 Choose b² {0, 1} M 1(x 1, b) (x 2, 0, x 2, 1), M 2(x 2, b) … (xk, 0, xk, 1), Mk Mk(xk, b) b = 0 is real world b=1 is world in which Bob’s data replaced with junk

Flavor of Privacy Proof A B

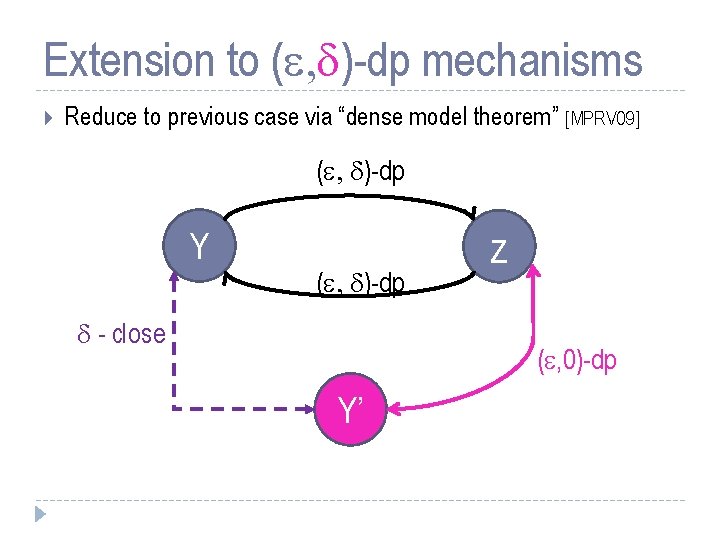
Extension to ( , d)-dp mechanisms Reduce to previous case via “dense model theorem” [MPRV 09] ( , d)-dp Y ( , d)-dp d - close z ( , 0)-dp Y’

Composition Theorem

Outline Part 1: Basics Part 2: Many Queries Sparse Vector Multiplicative Weights Boosting for queries Part 3: Techniques Smoking causes cancer Definition Laplace mechanism Simple composition Histogram example Advanced composition Exponential mechanism and application Subsample-and-Aggregate Propose-Test-Release Application of S&A and PTR combined Future Directions

Many Queries Sparse Vector; Private Multiplicative Weights, Boosting for Queries

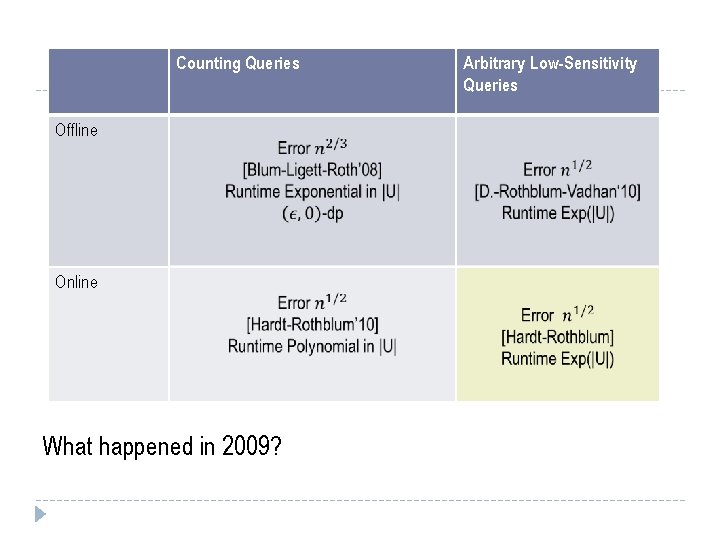
Counting Queries Arbitrary Low-Sensitivity Queries Offline Online Caveat: Omitting polylog(various things, some of them big) terms

Sparse Vector insignificant insig
![Algorithm and Privacy Analysis Caution Conditional branch leaks private information HardtRothblum Algorithm and Privacy Analysis Caution: Conditional branch leaks private information! • [Hardt-Rothblum]](https://slidetodoc.com/presentation_image_h/236d3379f989b846665d32f0d8de133b/image-28.jpg)
Algorithm and Privacy Analysis Caution: Conditional branch leaks private information! • [Hardt-Rothblum]

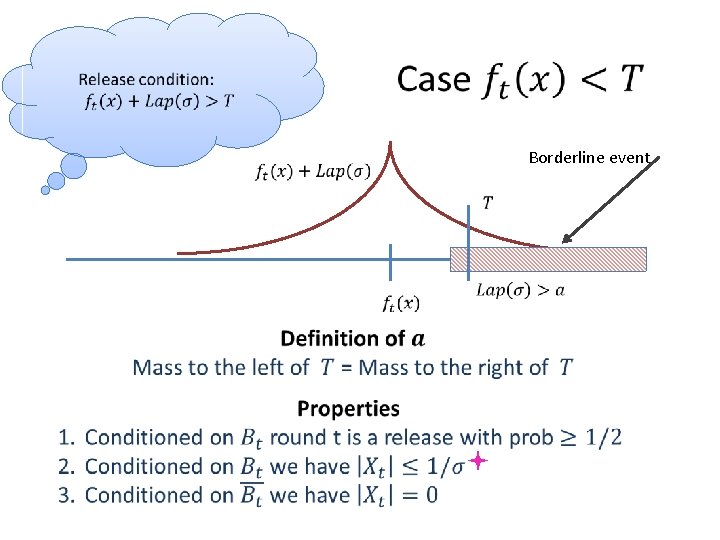
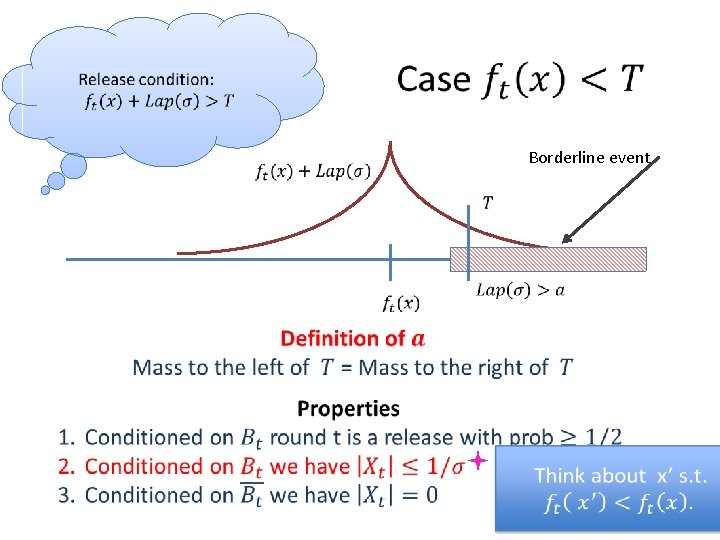
Algorithm and Privacy Analysis Caution: Conditional branch leaks private information! • • Intuition: counts far below T leak nothing – Only charge for noisy counts in this range:



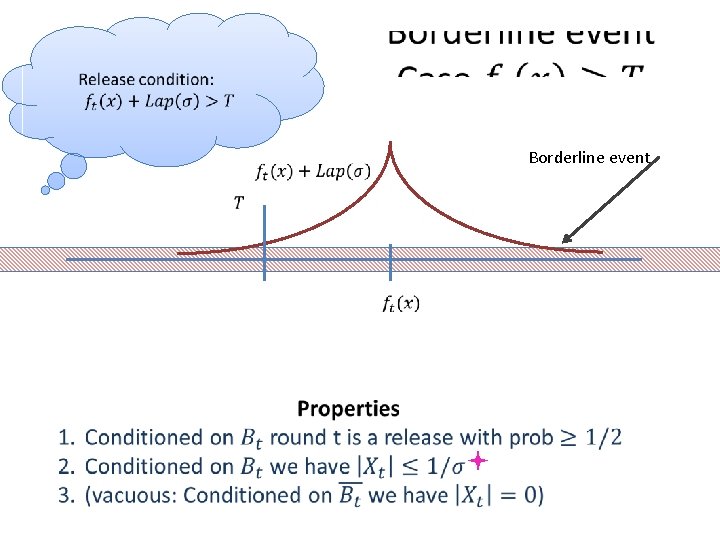
Borderline event

Borderline event

Borderline event


Wrapping Up: Sparse Vector Analysis
![Private Multiplicative Weights HardtRothblum 10 Represent database as normalized histogram on U Private Multiplicative Weights [Hardt-Rothblum’ 10] Represent database as (normalized) histogram on U](https://slidetodoc.com/presentation_image_h/236d3379f989b846665d32f0d8de133b/image-37.jpg)
Private Multiplicative Weights [Hardt-Rothblum’ 10] Represent database as (normalized) histogram on U

Multiplicative Weights

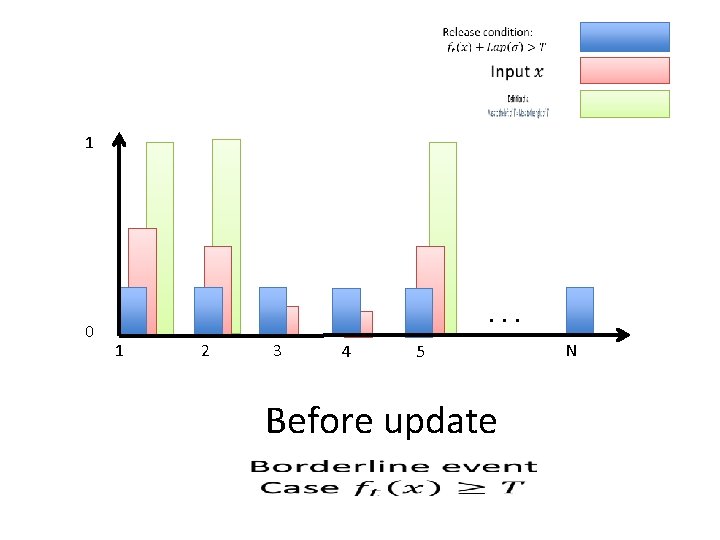
1 0 . . . 1 2 3 4 5 Before update N

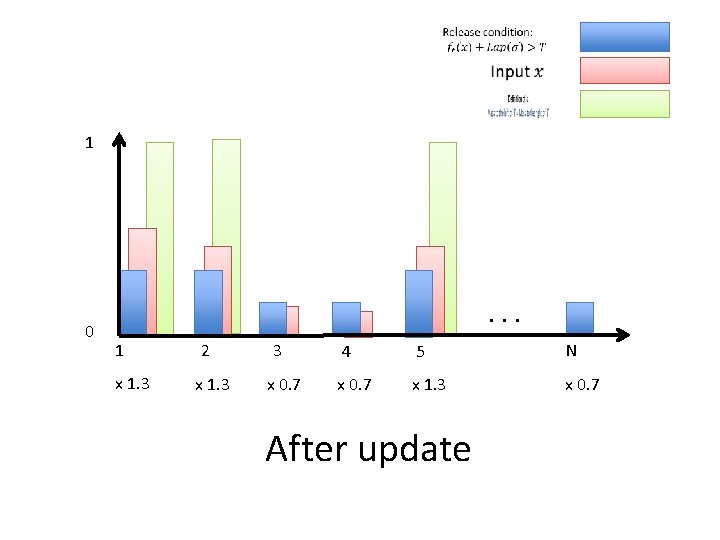
1 0 . . . 1 x 1. 3 2 x 1. 3 3 x 0. 7 4 5 N x 0. 7 x 1. 3 x 0. 7 After update


Analysis

Counting Queries Arbitrary Low-Sensitivity Queries Offline Online Caveat: Omitting polylog(various things, some of them big) terms
![Boosting Schapire 1989 General method for improving accuracy of any given learning algorithm Example Boosting [Schapire, 1989] General method for improving accuracy of any given learning algorithm Example:](https://slidetodoc.com/presentation_image_h/236d3379f989b846665d32f0d8de133b/image-44.jpg)
Boosting [Schapire, 1989] General method for improving accuracy of any given learning algorithm Example: Learning to recognize spam e-mail “Base learner” receives labeled examples, outputs heuristic Run many times; combine the resulting heuristics

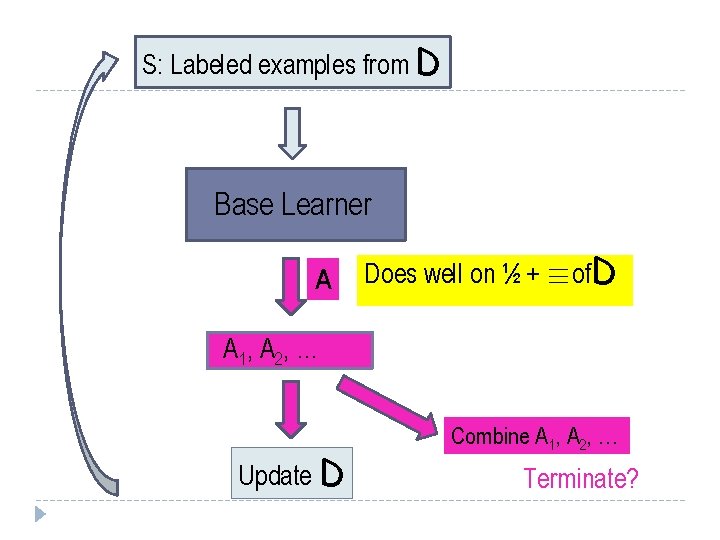
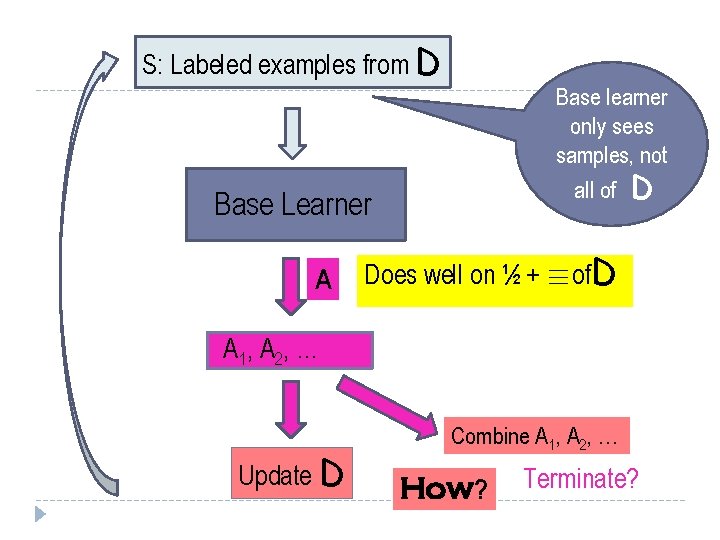
S: Labeled examples from D Base Learner A Does well on ½ + ´of. D A 1, A 2, … Update D Combine A 1, A 2, … Terminate?

S: Labeled examples from D Base learner only sees samples, not all of D Base Learner A Does well on ½ + ´of. D A 1, A 2, … Update D Combine A 1, A 2, … How? Terminate?

Boosting for Queries? Goal: Given database x and a set Q of low-sensitivity queries, produce an object O such that 8 q 2 Q : can extract from O an approximation of q(x). Assume existence of (² 0, ± 0)-dp Base Learner producing an object O that does well on more than half of D Pr q » D[ |q(O) – q(DB)| < ¸] > (1/2 + ´)

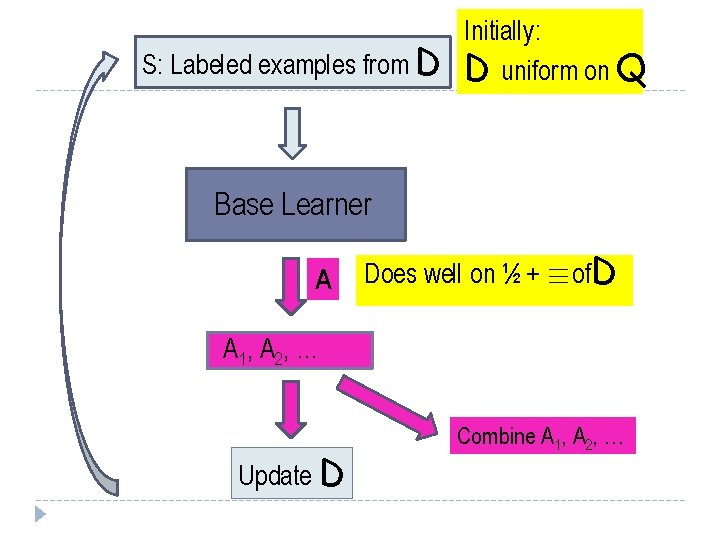
S: Labeled examples from D Initially: D uniform on Q Base Learner A Does well on ½ + ´of. D A 1, A 2, … Update D Combine A 1, A 2, …

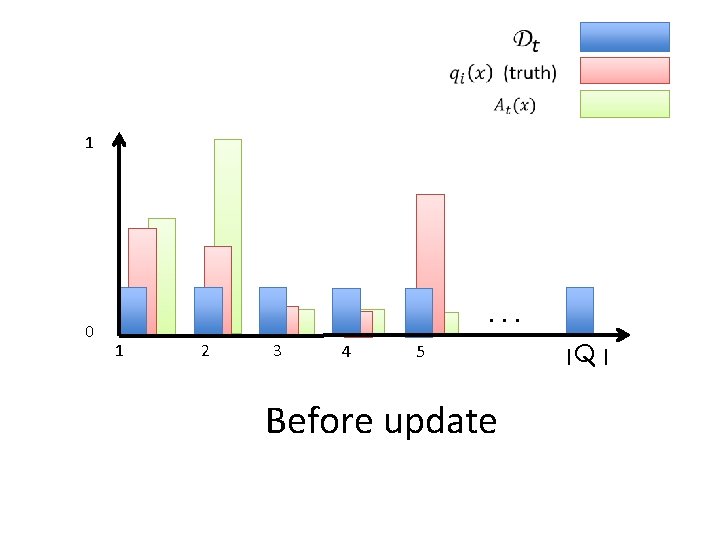
1 0 . . . 1 2 3 4 5 Before update |Q |

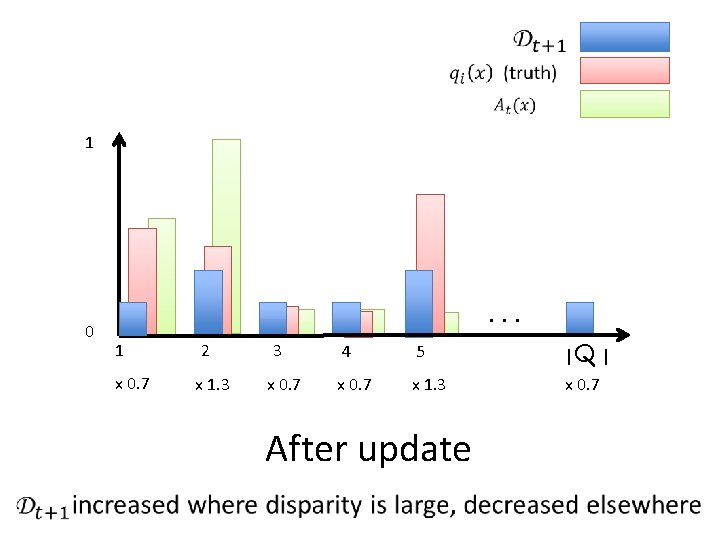
1 0 . . . 1 x 0. 7 2 x 1. 3 3 x 0. 7 4 5 |Q | x 0. 7 x 1. 3 x 0. 7 After update

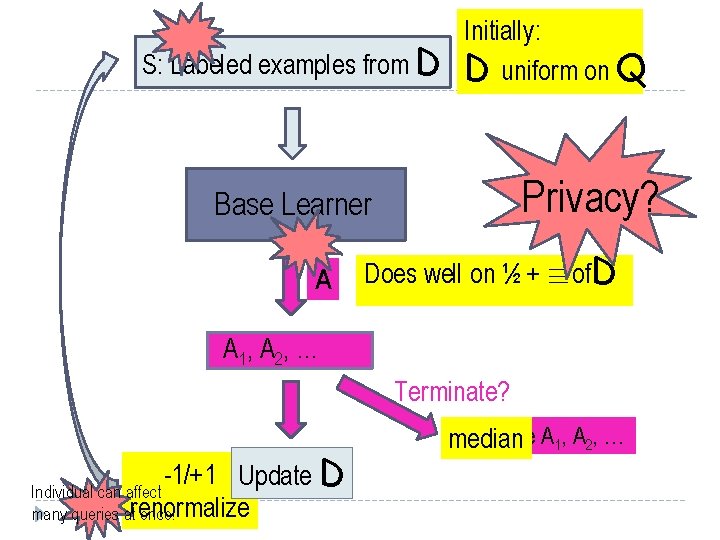
S: Labeled examples from D Initially: D uniform on Q Privacy? Base Learner A Does well on ½ + ´of. D A 1, A 2, … Terminate? -1/+1 Update D Individual can affect renormalize many queries at once! Combine A 1, A 2, … median

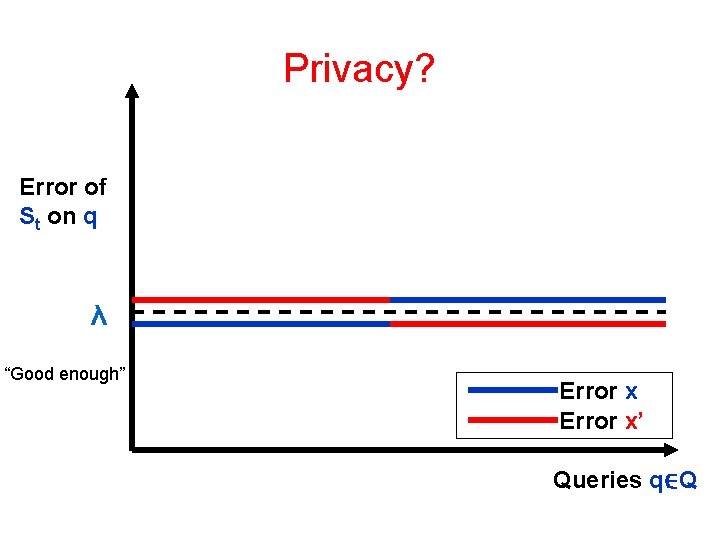
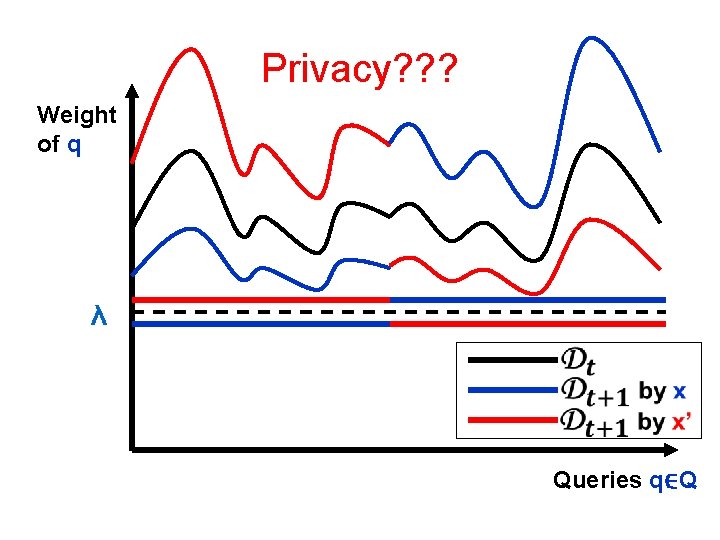
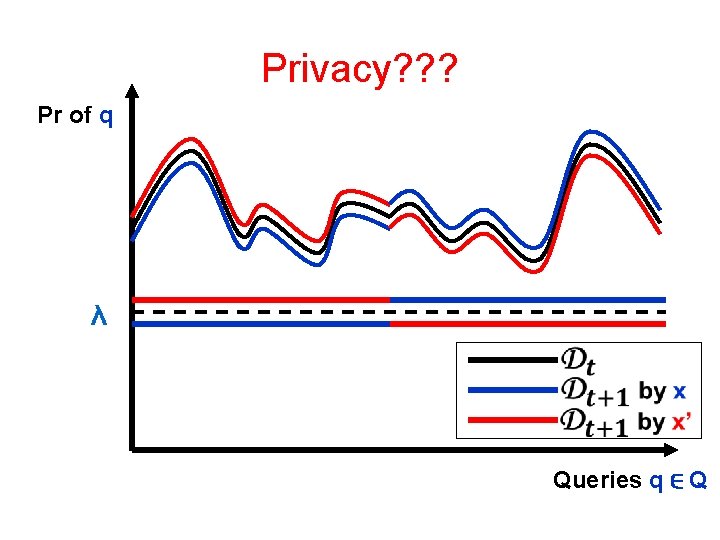
Privacy is Problematic

Privacy? Error of St on q λ “Good enough” Error x’ Queries q∈Q

Privacy? ? ? Weight of q λ Queries q∈Q
![Private Boosting for Queries Variant of Ada Boost Initial distribution D is uniform on Private Boosting for Queries [Variant of Ada. Boost] Initial distribution D is uniform on](https://slidetodoc.com/presentation_image_h/236d3379f989b846665d32f0d8de133b/image-55.jpg)
Private Boosting for Queries [Variant of Ada. Boost] Initial distribution D is uniform on queries in Q S is always a set of k elements drawn from Qk Combiner is median [viz. Freund 92] Attenuated Re-Weighting If very well approximated by At, decrease weight by factor of e (“-1”) If very poorly approximated by At, increase weight by factor of e (“+1”) In between, scale with distance of midpoint (down or up): 2 ( |q(DB) – q(At)| - (¸ + ¹/2) ) / ¹(sensitivity: 2½/¹) + (log |Q |3/2½√k) / ²´ 4
![Private Boosting for Queries Variant of Ada Boost Initial distribution D is uniform on Private Boosting for Queries [Variant of Ada. Boost] Initial distribution D is uniform on](https://slidetodoc.com/presentation_image_h/236d3379f989b846665d32f0d8de133b/image-56.jpg)
Private Boosting for Queries [Variant of Ada. Boost] Initial distribution D is uniform on queries in Q Reweighting similar under x and x’ Need lots of samples to detect difference S is always a set of k elements drawn from Qk Adversary never gets hands on lots of samples Combiner is median [viz. Freund 92] Attenuated Re-Weighting If very well approximated by At, decrease weight by factor of e (“-1”) If very poorly approximated by At, increase weight by factor of e (“+1”) In between, scale with distance of midpoint (down or up): 2 ( |q(DB) – q(At)| - (¸ + ¹/2) ) / ¹(sensitivity: 2½/¹) + (log |Q |3/2½√k) / ²´ 4

Privacy? ? ? Pr of q λ Queries q ∈ Q

Agnostic as to Type Signature of Q

Analyzing Privacy Loss Know that “the epsilons and deltas add up” T invocations of Base Generator ( base , ±base) Tk samples from distributions ( sample, ±sample) k each from D 1, … , DT Fair because samples in iteration t are mutually independent and distribution being sampled depends only on A 1, …, A t-1 (public) Improve on (T base + Tk sample , T±base +Tk ±sample)-dp via composition theorem

Counting Queries Arbitrary Low-Sensitivity Queries Offline Online Caveat: Omitting polylog(various things, some of them big) terms



Moral: To handle many databases must relax adversary assumptions or introduce coordination

Outline Part 1: Basics Part 2: Many Queries Sparse Vector Multiplicative Weights Boosting for queries Part 3: Techniques Smoking causes cancer Definition Laplace mechanism Simple composition Histogram example Advanced composition Exponential mechanism and application Subsample-and-Aggregate Propose-Test-Release Application of S&A and PTR combined Future Directions

Discrete-Valued Functions

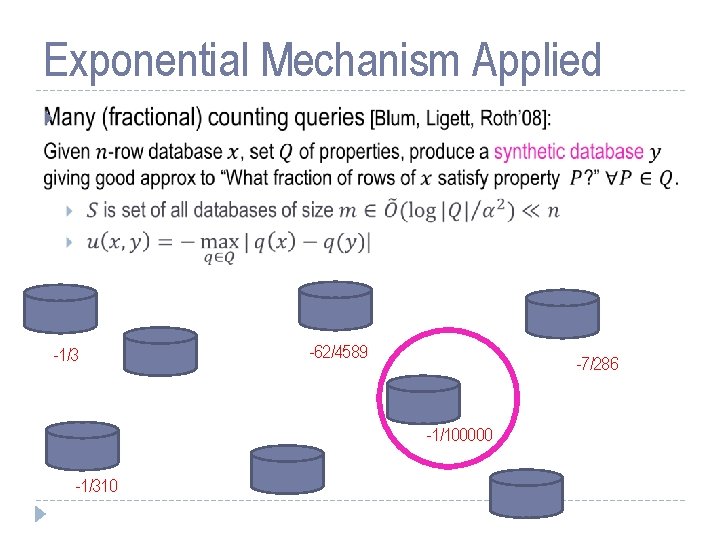
Exponential Mechanism Applied -1/3 -62/4589 -7/286 -1/100000 -1/310

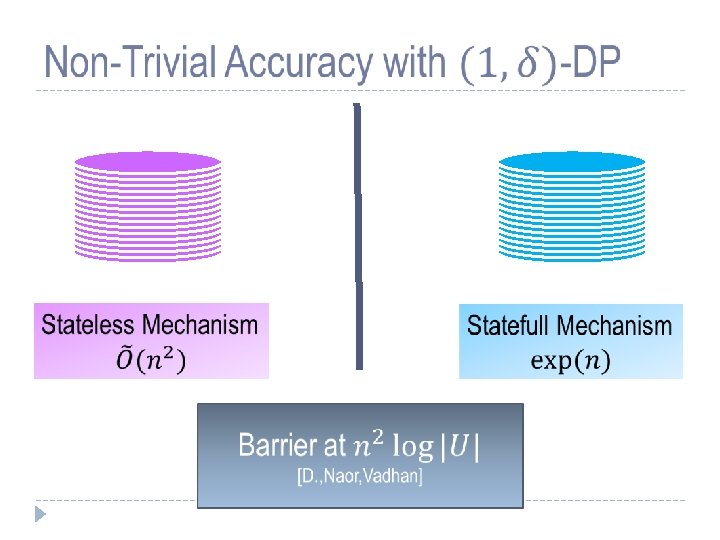
Counting Queries Arbitrary Low-Sensitivity Queries Offline Online What happened in 2009?
![HighUnknown Sensitivity Functions SubsampleandAggregate Nissim Raskhodnikova Smith 07 High/Unknown Sensitivity Functions Subsample-and-Aggregate [Nissim, Raskhodnikova, Smith’ 07]](https://slidetodoc.com/presentation_image_h/236d3379f989b846665d32f0d8de133b/image-68.jpg)
High/Unknown Sensitivity Functions Subsample-and-Aggregate [Nissim, Raskhodnikova, Smith’ 07]
![Functions Expected to Behave Well ProposeTestRelease D Lei 09 Privacypreserving test for goodness of Functions “Expected” to Behave Well Propose-Test-Release [D. -Lei’ 09] Privacy-preserving test for “goodness” of](https://slidetodoc.com/presentation_image_h/236d3379f989b846665d32f0d8de133b/image-69.jpg)
Functions “Expected” to Behave Well Propose-Test-Release [D. -Lei’ 09] Privacy-preserving test for “goodness” of data set Eg, low local sensitivity [Nissim-Raskhodnikova-Smith 07] Big gap …… Robust statistics theory: Lack of density at median is the only thing that can go wrong

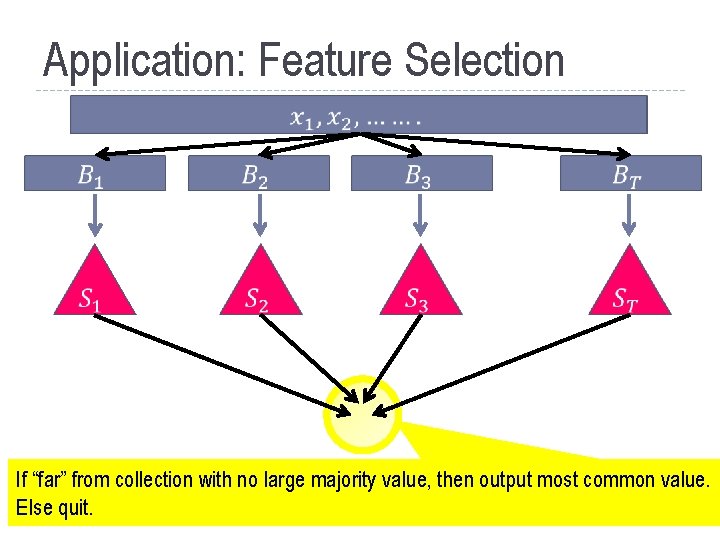
Application: Feature Selection If “far” from collection with no large majority value, then output most common value. Else quit.

Future Directions

Thank You! -4 R -3 R -2 R -R 0 R 2 R 3 R 4 R 5 R
 Cynthia dwork differential privacy
Cynthia dwork differential privacy Microsoft differential privacy
Microsoft differential privacy Privacy awareness and hipaa privacy training cvs answers
Privacy awareness and hipaa privacy training cvs answers Quantum differential privacy
Quantum differential privacy Differential privacy
Differential privacy Differential privacy
Differential privacy Complexity of differential privacy
Complexity of differential privacy Microsoft azure security privacy and compliance
Microsoft azure security privacy and compliance Microsoft office privacy settings popup
Microsoft office privacy settings popup Edge startwarren theverge
Edge startwarren theverge Microsof excel merupakan program aplikasi
Microsof excel merupakan program aplikasi Microsoft official academic course microsoft word 2016
Microsoft official academic course microsoft word 2016 Microsoft official academic course microsoft word 2016
Microsoft official academic course microsoft word 2016 Microsoft official academic course microsoft excel 2016
Microsoft official academic course microsoft excel 2016 Cynthia lightfoot
Cynthia lightfoot Cynthia polk johnson
Cynthia polk johnson Trashketball directions
Trashketball directions Cynthia arndell md
Cynthia arndell md Cynthia cooper (accountant)
Cynthia cooper (accountant) 8 854x10^-12
8 854x10^-12 Cynthia bergman
Cynthia bergman Rules cynthia lord
Rules cynthia lord Cynthia rivera nj
Cynthia rivera nj Cynthia couto
Cynthia couto Cynthia kieffer
Cynthia kieffer Cynthia jane anderson
Cynthia jane anderson Cynthia santamaria
Cynthia santamaria Cynthia jackevicius
Cynthia jackevicius Cynthia gatewood
Cynthia gatewood Stray'' by cynthia rylant point of view
Stray'' by cynthia rylant point of view Cynthia cooper
Cynthia cooper Cynthia caron
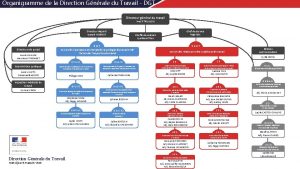
Cynthia caron Direction générale du travail
Direction générale du travail Cynthia freelund sexy
Cynthia freelund sexy Cynthia nediyakalayil
Cynthia nediyakalayil Cynthia freeland football
Cynthia freeland football Dr cynthia quainoo
Dr cynthia quainoo Slidetodoc.com
Slidetodoc.com Cynthia youngblood
Cynthia youngblood Cynthia vant hul
Cynthia vant hul Cynthia agustin
Cynthia agustin Cynthia weber international relations theory
Cynthia weber international relations theory Dr cynthia lim
Dr cynthia lim Cynthia hale birthday
Cynthia hale birthday Dr. cynthia warrick
Dr. cynthia warrick Cynthia lee sheng
Cynthia lee sheng Cynthia švrlingová
Cynthia švrlingová Cynthia cooper (accountant)
Cynthia cooper (accountant) Cynthia vallerand
Cynthia vallerand Family tree princess diana
Family tree princess diana Cynthia atterberry
Cynthia atterberry Cynthia thomas md
Cynthia thomas md Cynthia tay
Cynthia tay Introduction of school health services
Introduction of school health services Cynthia shanahan
Cynthia shanahan Dr cynthia lynch
Dr cynthia lynch Cynthia nagendra
Cynthia nagendra Cynthia furse
Cynthia furse Cynthia lundberg
Cynthia lundberg Cynthia talavera
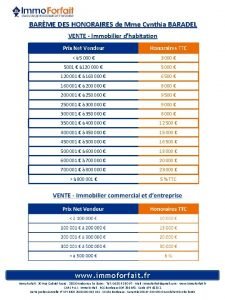
Cynthia talavera Cynthia baradel
Cynthia baradel Rules by cynthia lord read aloud
Rules by cynthia lord read aloud Supa forensics
Supa forensics Cynthia fung chen
Cynthia fung chen Moon goddess cynthia
Moon goddess cynthia Tư thế ngồi viết
Tư thế ngồi viết Cái miệng nó xinh thế chỉ nói điều hay thôi
Cái miệng nó xinh thế chỉ nói điều hay thôi Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Cách giải mật thư tọa độ
Cách giải mật thư tọa độ Bổ thể
Bổ thể Tư thế ngồi viết
Tư thế ngồi viết Ví dụ giọng cùng tên
Ví dụ giọng cùng tên Thẻ vin
Thẻ vin