First order differential equations Introduction In this chapter

First order differential equations

Introduction • In this chapter you will learn how to solve differential equations • There are various techniques including use of an integrating factor • Models like these allow the more detailed study of areas such as population growth, and optimisation of medical treatments!

Teachings for Exercise 4 A

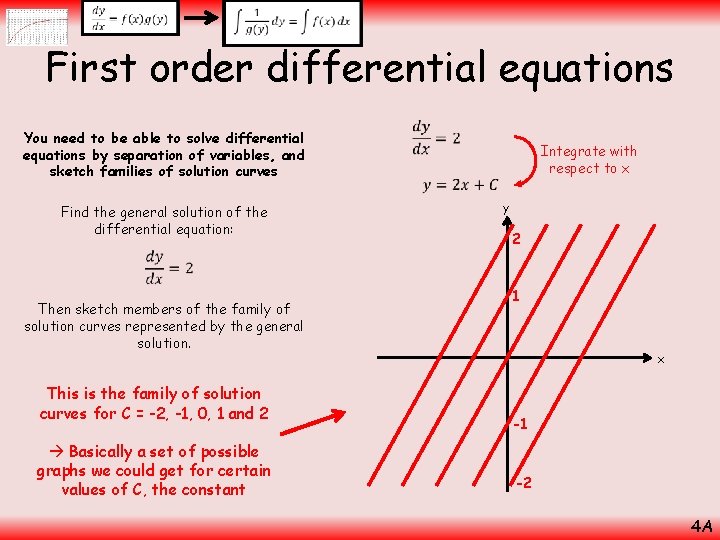
First order differential equations You need to be able to solve differential equations by separation of variables, and sketch families of solution curves In C 4 you have solved equations using the ‘separation of variables’ technique Remember what this looks like? Divide by g(y) and multiply by dx Integrate both sides Once integrated, you will be left with an equation that you can rearrange to put in different forms Remember that the ‘+C’ part could be anything at this stage. The possible functions are known as a ‘family of solution curves’ You can also find ‘particular’ solutions if you are told information linking x and y 4 A

First order differential equations You need to be able to solve differential equations by separation of variables, and sketch families of solution curves Find the general solution of the differential equation: Then sketch members of the family of solution curves represented by the general solution. This is the family of solution curves for C = -2, -1, 0, 1 and 2 Basically a set of possible graphs we could get for certain values of C, the constant Integrate with respect to x y 2 1 x -1 -2 4 A

First order differential equations You need to be able to solve differential equations by separation of variables, and sketch families of solution curves Find the general solution of the differential equation: In this case you will need to separate the variables x and y before you can Integrate As 2 C is just a number, we can think of it as being the ‘r 2’ part of the circle equation Integrate both sides Then sketch members of the family of solution curves represented by the general solution. Multiply by y and multiply by dx Calculate Add 1/2 x Multiply by 2 Hopefully you recognise this as the equation of a circle! r 2 = 2 C 4 A

First order differential equations You need to be able to solve differential equations by separation of variables, and sketch families of solution curves The original equation… Find the general solution of the differential equation: y 6 Then sketch members of the family of solution curves represented by the general solution. Now we have the equation we can sketch some examples from this ‘family’ 3 2 1 x These curves correspond to C = 0. 5, 1, 1. 5 and 3 respectively (as the equation has 2 C in it!) 4 A

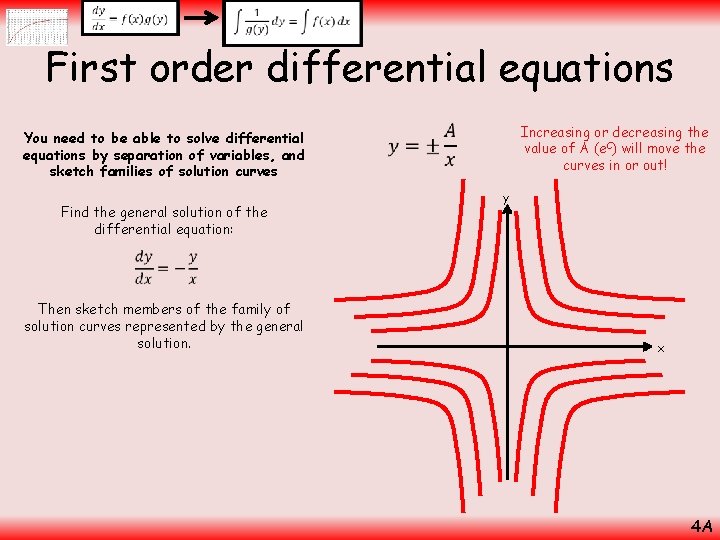
First order differential equations You need to be able to solve differential equations by separation of variables, and sketch families of solution curves Divide by y, multiply by dx Find the general solution of the differential equation: Integrate each side Then sketch members of the family of solution curves represented by the general solution. Calculate the integrals This step is common – ie) the replacing of a constant involving several letters with a single, different letter Make sure it is clear when you do this! Remember you cannot replace a ‘variable’ term such as ‘x’ in this way! Add lnx Use the multiplication law Take exponentials of each side (cancels the ‘ln’ – we will explain the modulus in a moment!) Divide by x (remember the modulus gives a positive or negative possibility) Replace e. C with ‘A’ as e. C is just a constant 4 A

First order differential equations You need to be able to solve differential equations by separation of variables, and sketch families of solution curves Why did we have to include a modulus here? This is the equation we ended up with when using the modulus Find the general solution of the differential equation: If positive If negative Rewrite Then sketch members of the family of solution curves represented by the general solution. Both possibilities differentiate to give us the original function, so therefore we need to include the modulus or we would lose an answer! Take exponentials of each side Rewrite Differentiate If y = A/x, A = xy Group x’s Rewrite Differentiate If y = -A/x, A = -xy Group x’s Rewrite 4 A

First order differential equations You need to be able to solve differential equations by separation of variables, and sketch families of solution curves Find the general solution of the differential equation: Increasing or decreasing the value of A (e. C) will move the curves in or out! y Then sketch members of the family of solution curves represented by the general solution. x 4 A

First order differential equations You need to be able to solve differential equations by separation of variables, and sketch families of solution curves Find the general solution of the differential equation: Divide by √x, multiply by dt Rewrite as powers (if needed) Take Integrals of each side Calculate And then find the particular solution if x = 9 when t = 0. As always, start by separating the variables and integrating The difference in this questions is that you will be able to find the value of the constant, C Rewrite left side Divide by 2 Sub in x = 9 when t = 0 Remember √ 9 means ‘positive square root’ Calculate 4 A

First order differential equations You need to be able to solve differential equations by separation of variables, and sketch families of solution curves Find the general solution of the differential equation: Sub in C = 6 which we worked out Square both sides And then find the particular solution if x = 9 when t = 0. As always, start by separating the variables and integrating The difference in this questions is that you will be able to find the value of the constant, C 4 A

Teachings for Exercise 4 B

First order differential equations You can solve exact equations where one side is the exact derivative of a product, and the other side can be integrated with respect to x The product rule Imagine we were finding: Find the general solution of the following equation: In this example you will not be able to separate the variables easily, if at all! You can use a pattern from the product rule however… (so u = x 3 and v = y) We can use the product rule above Sub in the values to the right Notice that d/dx(x 3 y) is equivalent to the left side of the original equation This means we can replace it! Replace the left hand side with equivalent expression 4 B

First order differential equations You can solve exact equations where one side is the exact derivative of a product, and the other side can be integrated with respect to x Find the general solution of the following equation: In this example you will not be able to separate the variables easily, if at all! You can use a pattern from the product rule however… Replace the left hand side with equivalent expression Take integrals of each side On the left side, the integral and differential cancel each other On the right side calculate the integral of sinx Divide by x 3 Other forms of this answer, such as the one below, are also fine! 4 B

First order differential equations You can solve exact equations where one side is the exact derivative of a product, and the other side can be integrated with respect to x You can use a general pattern to see whether this is doable. It is possible if the conditions to the right are met. If the conditions are met, you can change the expression on the left side to: General pattern This function of x… … differentiates to this function of x … differentiates to this function of y (with respect to x) This function of y… To put this using ‘proper’ mathematical notation… 4 B

First order differential equations You can solve exact equations where one side is the exact derivative of a product, and the other side can be integrated with respect to x Using mathematical notation General pattern Can be written as: The most common one you’ll see is: Can be written as: 4 B

First order differential equations You can solve exact equations where one side is the exact derivative of a product, and the other side can be integrated with respect to x Imagine the first part was split up – we can see the pattern will work! Find the general solution of the following differential equation: Rewrite the left side using the rule you have seen Take integrals of each side At a first glance it might look like the pattern will not work here 6 x 2 does not differentiate to 6 x, and y 2 does not differentiate to ydy/dx However, if we split up part of the equation, we can see that the pattern does work Calculate Divide by 3 x 2 Square root (or just leave as it is with y 2!) 4 B

Teachings for Exercise 4 C

First order differential equations • Multiply all terms by 4 x 2 Simplify each one Rewrite now using the pattern from 4 B Take integrals of each side Calculate Divide by 4 x 2 Alternative form (either is fine) 4 C

First order differential equations • 4 C

First order differential equations • Multiply by f(x) The idea is to produce an ‘exact’ equation which follows the pattern we know Now since we have produced an exact equation, the left side must now equal the general pattern from before The second terms must be equal if the sides are equal Divide by y Divide by f(x) 4 C

First order differential equations • The right side is a ‘standard pattern’ Take integrals of each side Take exponentials of each side 4 C

First order differential equations • Sub in the value of P Calculate the Integral So to make our differential equation exact, we need to multiply all terms by e-4 x 4 C

First order differential equations So to make our differential equation exact, we need to multiply all terms by e-4 x • Multiply all by e-4 x Differentiating e-4 x would give -4 e-4 x, so you can see the left side is now an exact equation Hence, we can rewrite it! We can also simplify the right side We are multiplying so add the powers together Integrate each side – cancels d/ dx on the left Calculate the integral on the right side Multiply by e 4 x (same as dividing by e-4 x) 4 C

First order differential equations • Divide all terms by cosx Sinx becomes tanx, cos 4 x becomes cos 3 x Now it is in the correct form, we can see the value of P is 2 tanx… Sub in the value of P Integrate (this one is in the formula booklet!) Use the power law The e and ln cancel out (this often happens in these questions!) So we need to multiply each part of the equation by sec 2 x (at the stage where it had only dy/dx at the front) 4 C

First order differential equations • Divide all terms by cosx Sinx becomes tanx, cos 4 x becomes cos 3 x Multiply by sec 2 x As sec 2 x = 1/cos 2 x, the right hand side can be simplified Combine the left side into a single differential as you have seen Integrate – cancels out the d/dx Calculate the right side Divide by sec 2 x (same as multiplying by cos 2 x) 4 C

Teachings for Exercise 4 D

First order differential equations You can use a given substitution to reduce a differential equation into one of the earlier types of equation, which you can then solve Use the substitution z = y/x to transform the differential equation: into a differential equation in x and z. By solving this equation, find the general solution of the original equation, writing y 2 in terms of x. As we are turning this into an equation in x and z, we are wanting to remove y We need an expression for y in terms of x and z, as well as an expression for dy/ dx in terms of x and z Use the substitution first to find these Multiply by x Use the product rule Now we have expressions for y and dy/dx, we can replace them in the differential equation to eliminate the y terms Replace y and dy/ dx terms Simplify You can divide all of the fraction on the right by x 2 4 D

First order differential equations You can use a given substitution to reduce a differential equation into one of the earlier types of equation, which you can then solve Use the substitution z = y/x to transform the differential equation: into a differential equation in x and z. By solving this equation, find the general solution of the original equation, writing y 2 in terms of x. We need an expression for y in terms of x and z, as well as an expression for dy/ dx in terms of x and z Combine fractions As we are turning this into an equation in x and z, we are wanting to remove y Multiply ‘z’ by 2 z/2 z so it can be combined Subtract z In this case, we can easily separate the variables! Divide by x, multiply by dx Divide by the ‘z’ based fraction (effectively flipping it as it moves across) Now we take integrals Use the substitution first to find these 4 D

First order differential equations You can use a given substitution to reduce a differential equation into one of the earlier types of equation, which you can then solve Use the substitution z = y/x to transform the differential equation: into a differential equation in x and z. By solving this equation, find the general solution of the original equation, writing y 2 in terms of x. As we are turning this into an equation in x and z, we are wanting to remove y We need an expression for y in terms of x and z, as well as an expression for dy/ dx in terms of x and z Integrate both sides – the left is a ‘standard pattern’ from C 4 C will be equal to ln of a number (let’s call it A) Combine the logarithms on the right Now you can remove the logarithms completely Replace z using the original substitution (to bring y back in) Subtract 1 Multiply by x 2 Use the substitution first to find these 4 D

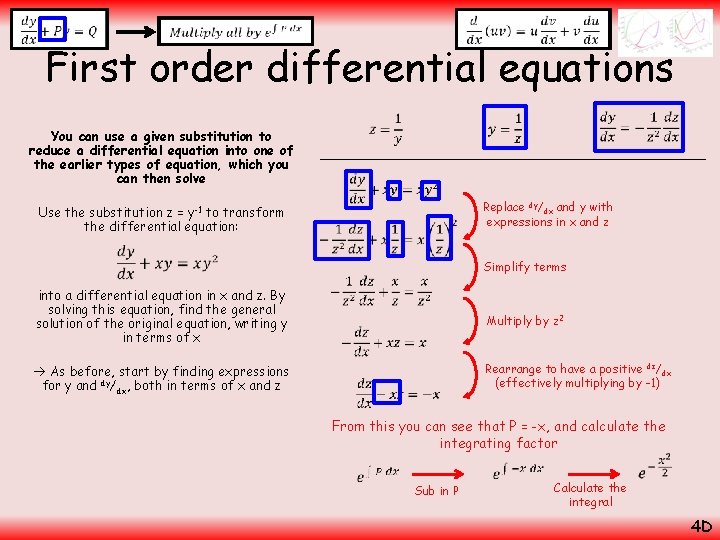
First order differential equations You can use a given substitution to reduce a differential equation into one of the earlier types of equation, which you can then solve Use the substitution z = y-1 to transform the differential equation: into a differential equation in x and z. By solving this equation, find the general solution of the original equation, writing y in terms of x Rewrite Multiply by y, Divide by z Rewrite Differentiate with respect to x (remember to include dz/dx on the right side) Rewrite As before, start by finding expressions for y and dy/dx, both in terms of x and z 4 D

First order differential equations You can use a given substitution to reduce a differential equation into one of the earlier types of equation, which you can then solve Use the substitution z = y-1 to transform the differential equation: Replace dy/dx and y with expressions in x and z into a differential equation in x and z. By solving this equation, find the general solution of the original equation, writing y in terms of x As before, start by finding expressions for y and dy/dx, both in terms of x and z Simplify terms Multiply by z 2 Rearrange to have a positive dz/dx (effectively multiplying by -1) From this you can see that P = -x, and calculate the integrating factor Sub in P Calculate the integral 4 D

First order differential equations You can use a given substitution to reduce a differential equation into one of the earlier types of equation, which you can then solve Use the substitution z = y-1 to transform the differential equation: into a differential equation in x and z. By solving this equation, find the general solution of the original equation, writing y in terms of x As before, start by finding expressions for y and dy/dx, both in terms of x and z Multiply by the integrating factor The left side can now be grouped as a single differential as we have seen Take integrals of both sides (cancels the d/dx) This is another ‘standard pattern’ Start with this expression and differentiate it Differentiating this gives the expression we are integrating So this is the integral we want! Always look for standard patterns first If you can’t find one, only then try using ‘integration by parts’ 4 D

First order differential equations You can use a given substitution to reduce a differential equation into one of the earlier types of equation, which you can then solve Use the substitution z = y-1 to transform the differential equation: into a differential equation in x and z. By solving this equation, find the general solution of the original equation, writing y in terms of x As before, start by finding expressions for y and dy/dx, both in terms of x and z Multiply by the integrating factor The left side can now be grouped as a single differential as we have seen Take integrals of both sides (cancels the d/dx) Use the integral we found z = y-1 so z = 1/y Rearrange (flip both sides effectively) 4 D

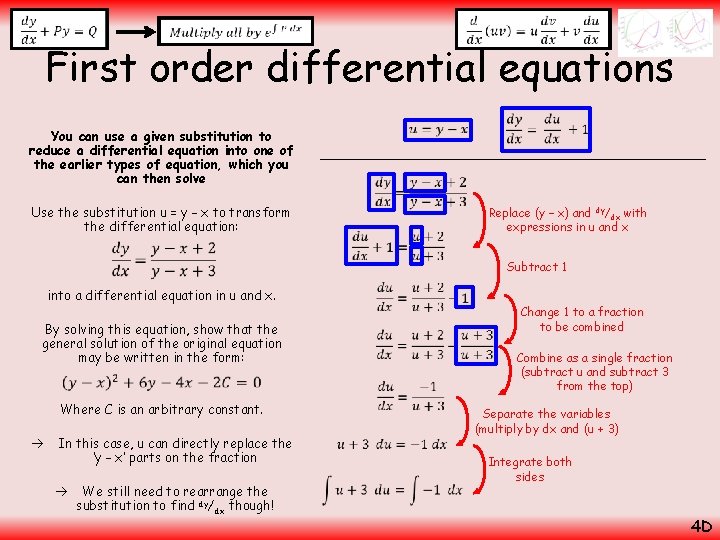
First order differential equations You can use a given substitution to reduce a differential equation into one of the earlier types of equation, which you can then solve Use the substitution u = y – x to transform the differential equation: Add x Swap round (you might not need to do this actually!) Differentiate into a differential equation in u and x. By solving this equation, show that the general solution of the original equation may be written in the form: Where C is an arbitrary constant. In this case, u can directly replace the ‘y – x’ parts on the fraction We still need to rearrange the substitution to find dy/dx though! 4 D

First order differential equations You can use a given substitution to reduce a differential equation into one of the earlier types of equation, which you can then solve Subtract 1 into a differential equation in u and x. By solving this equation, show that the general solution of the original equation may be written in the form: Where C is an arbitrary constant. In this case, u can directly replace the ‘y – x’ parts on the fraction We still need to rearrange the substitution to find dy/dx though! Replace (y – x) and dy/dx with expressions in u and x Use the substitution u = y – x to transform the differential equation: Change 1 to a fraction to be combined Combine as a single fraction (subtract u and subtract 3 from the top) Separate the variables (multiply by dx and (u + 3) Integrate both sides 4 D

First order differential equations You can use a given substitution to reduce a differential equation into one of the earlier types of equation, which you can then solve Use the substitution u = y – x to transform the differential equation: into a differential equation in u and x. By solving this equation, show that the general solution of the original equation may be written in the form: Integrate both sides Replace u with y-x Multiply all by 2 Expand the bracket Add 2 x, subtract 2 C Where C is an arbitrary constant. In this case, u can directly replace the ‘y – x’ parts on the fraction We still need to rearrange the substitution to find dy/dx though! 4 D

Summary • You have learnt how to solve first order differential equations • We have seen several methods for this and the drawing of solution curves • Ensure your knowledge of C 4 Integration is solid as it helps a lot with these!