Ordinary Differential Equations ODEs Differential equations are the

Ordinary Differential Equations (ODEs) • Differential equations are the ubiquitous, the lingua franca of the sciences; many different fields are linked by having similar differential equations • ODEs have one independent variable; PDEs have more • Examples: electrical circuits Newtonian mechanics chemical reactions population dynamics economics… and so on, ad infinitum

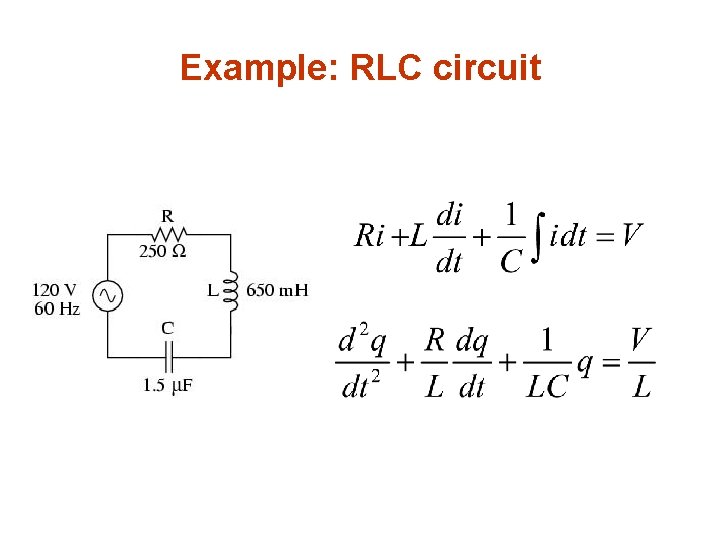
Example: RLC circuit

To illustrate: Population dynamics • 1798 Malthusian catastrophe • 1838 Verhulst, logistic growth • Predator-prey systems, Volterra-Lotka

Population dynamics • Malthus: • Verhulst: Logistic growth

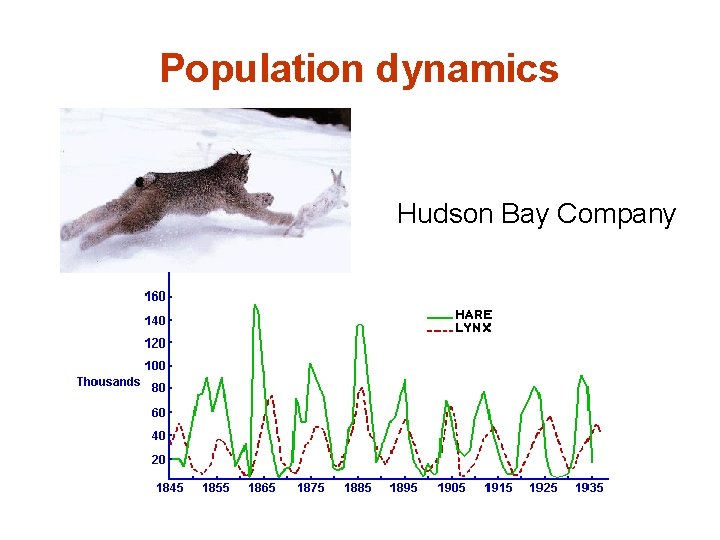
Population dynamics Hudson Bay Company

Population dynamics V. Volterra, commercial fishing in the Adriatic

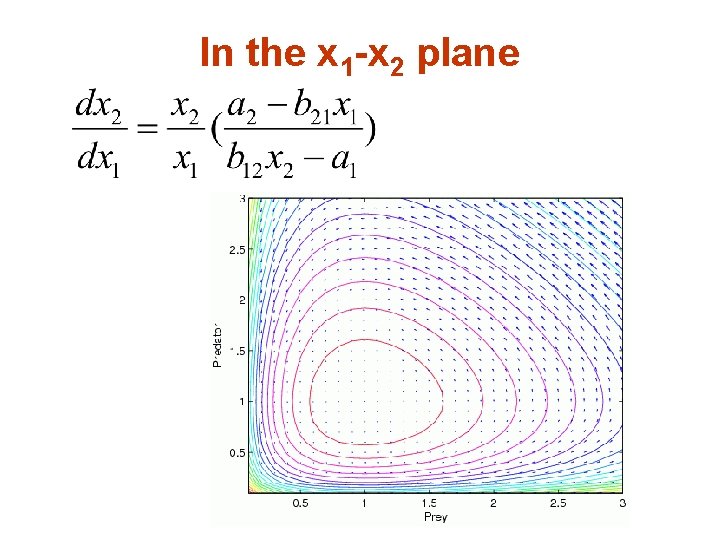
In the x 1 -x 2 plane

State space Integrate analytically! Produces a family of concentric closed curves as shown… How to compute?

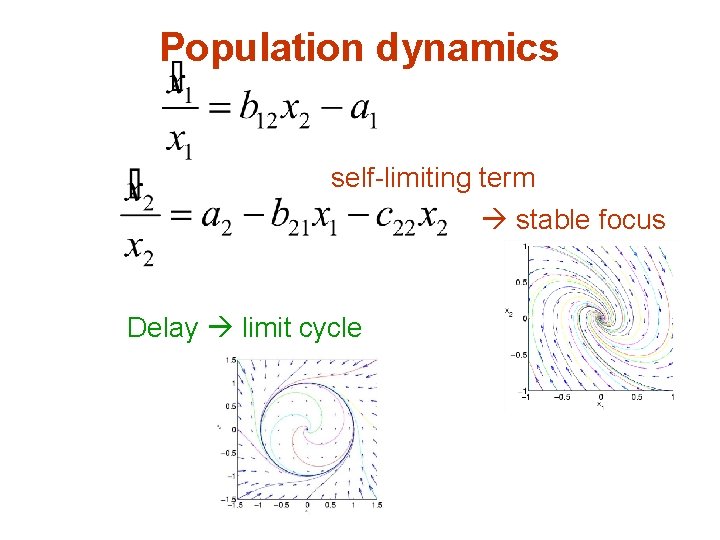
Population dynamics self-limiting term stable focus Delay limit cycle

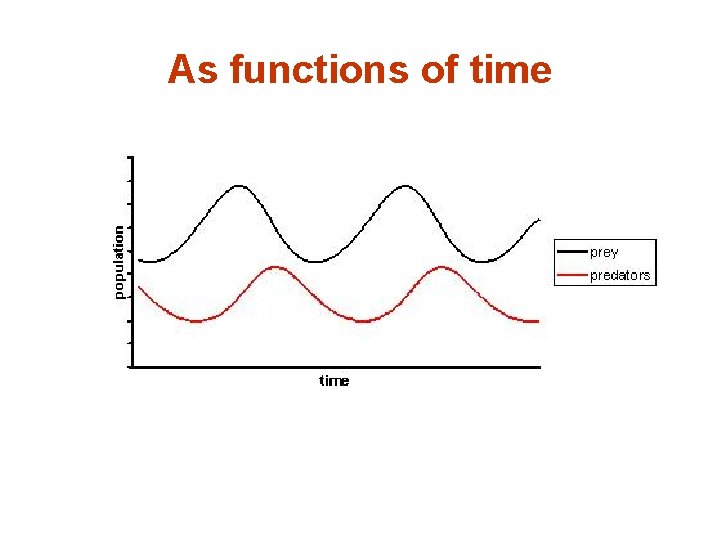
As functions of time

Do you believe this? • Do hares eat lynx, Gilpin 1973 Do Hares Eat Lynx? Michael E. Gilpin The American Naturalist, Vol. 107, No. 957 (Sep. - Oct. , 1973), pp. 727 -730 Published by: The University of Chicago Press for The American Society of Naturalists Stable URL: http: //www. jstor. org/stable/2459670

Putting equations in state-space form

Traditional state space: Example: the (nonlinear) pendulum Mc. Master

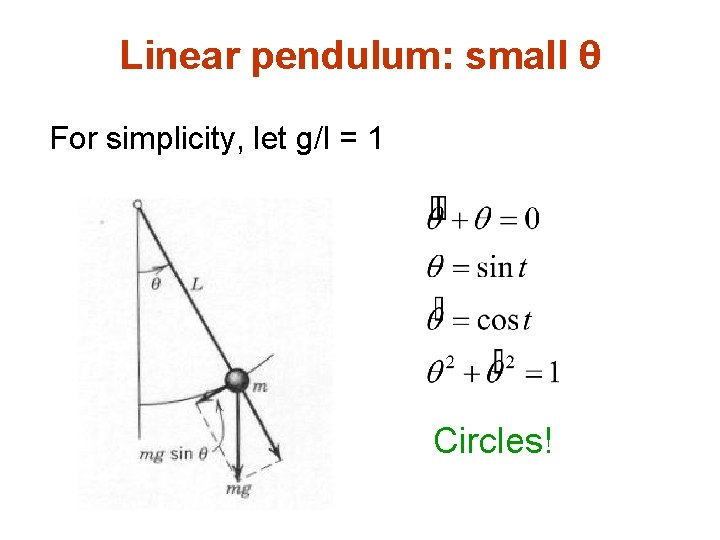
Linear pendulum: small θ For simplicity, let g/l = 1 Circles!

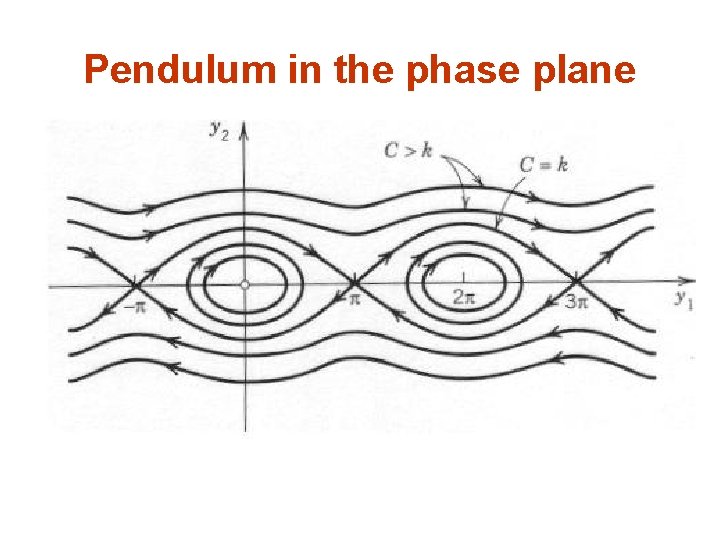
Pendulum in the phase plane

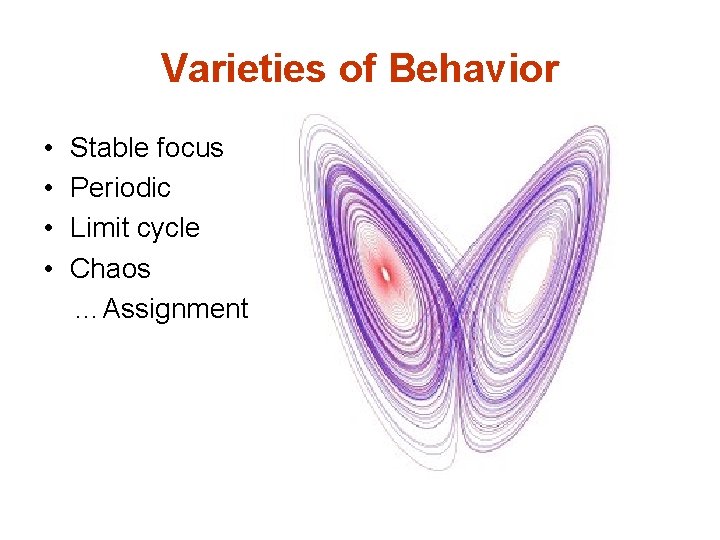
Varieties of Behavior • Stable focus • Periodic • Limit cycle

Varieties of Behavior • • Stable focus Periodic Limit cycle Chaos …Assignment

Numerical integration of ODEs • Euler’s Method simple-minded, basis of many others • Predictor-corrector methods can be useful • Runge-Kutta (usually 4 th-order) workhorse, good enough for our work, but not state-of-the-art

Criteria for evaluating • Accuracy use Taylor series, big-Oh, classical numerical analysis • Efficiency running time may be hard to predict, sometimes step size is adaptive • Stability some methods diverge on some problems

Euler • Local error = O(h 2) • Global accumulated) error = O(h) (Roughly: multiply by T/h )

Euler • Local error = O(h 2) • Global (accumulated) error = O(h) Euler step

Euler • Local error = O(h 2) • Global (accumulated) error = O(h) Euler step Taylor’s series with remainder

Second-order Runge-Kutta (midpoint method) • Local error = O(h 3) • Global (accumulated) error = O(h 2)

Fourth-order Runge-Kutta • Local error = O(h 5) • Global (accumulated) error = O(h 4)

Additional topics • Stability, stiff systems • Implicit methods • Two-point boundary-value problems shooting methods relaxation methods