Modern Control System EKT 308 General Introduction Introduction














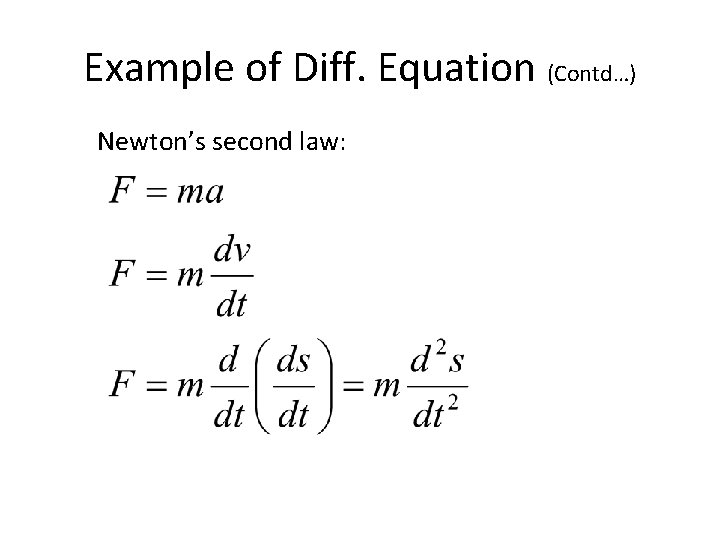

















- Slides: 45

Modern Control System EKT 308 • General Introduction • Introduction to Control System • Brief Review - Differential Equation - Laplace Transform

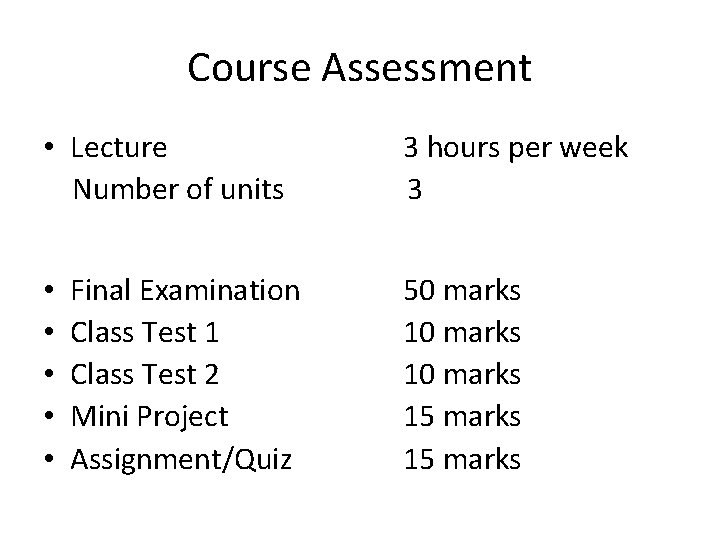
Course Assessment • Lecture Number of units • • • Final Examination Class Test 1 Class Test 2 Mini Project Assignment/Quiz 3 hours per week 3 50 marks 10 marks 15 marks

Course Outcomes • CO 1: : The ability to obtain the mathematical model for electrical and mechanical systems and solve state equations. • CO 2: : The ability to perform time domain analysis with response to test inputs and to determine the stability of the system. • CO 3: The ability to perform frequency domain analysis of linear system and to evaluate its stability using frequency domain methods. • CO 4: The ability to design lag, lead-lag compensators for linear control systems.

Lecturer Dr. Md. Mijanur Rahman mijanur@unimap. edu. my 016 6781633

Text Book References • Dorf, Richard C. , Bishop, Robert H. , “Modern Control Systems”, Pearson, Twelfth Edition, 2011 • Nise , Norman S. , “Control Systems Engineering”, John Wiley and Sons , Fourth Edition, 2004. • Kuo B. C. , "Automatic Control Systems", Prentice Hall, 8 th Edition, 1995 • Ogata, K, "Modern Control Engineering"Prentice Hall, 1999 • Stanley M. Shinners, “Advanced Modern Control System Theory and Design”, John Wiley and Sons, 2 nd Edition. 1998

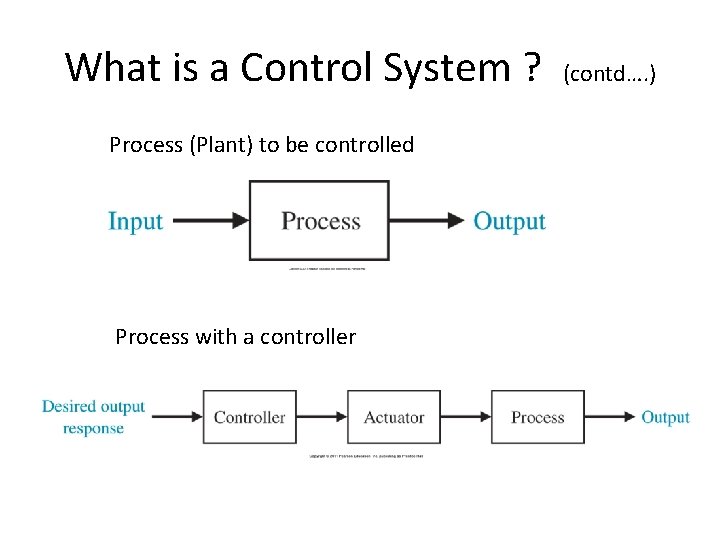
What is a Control System ? • A device or a set of devices • Manages, commands, directs or regulates the behavior of other devices or systems.

What is a Control System ? Process (Plant) to be controlled Process with a controller (contd…. )

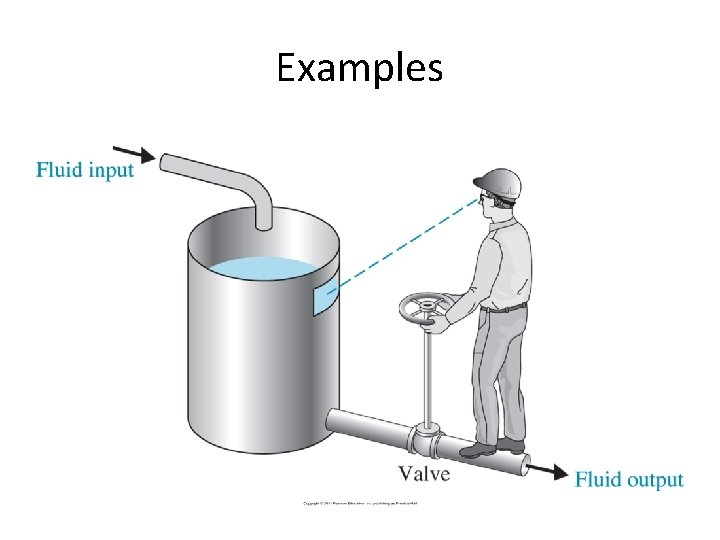
Examples

Examples (contd…) Human Control

System Control

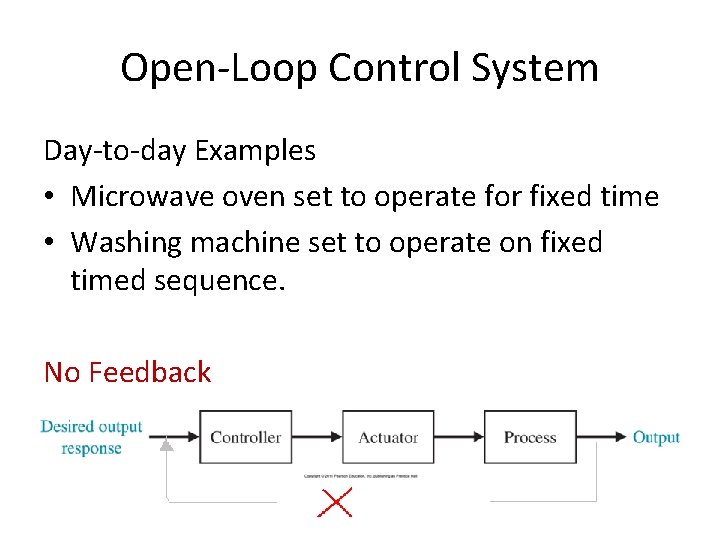
Classification of Control Systems Control systems are often classified as • Open-loop Control System • Closed-Loop Control Systems Also called Feedback or Automatic Control System

Open-Loop Control System Day-to-day Examples • Microwave oven set to operate for fixed time • Washing machine set to operate on fixed timed sequence. No Feedback

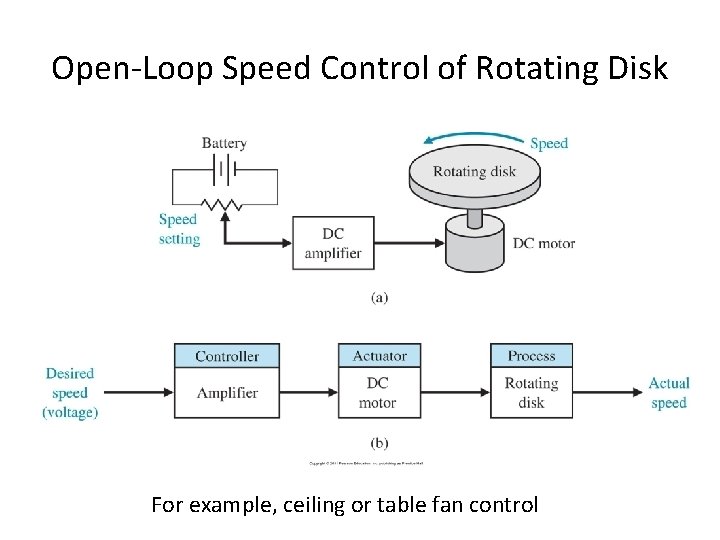
Open-Loop Speed Control of Rotating Disk For example, ceiling or table fan control

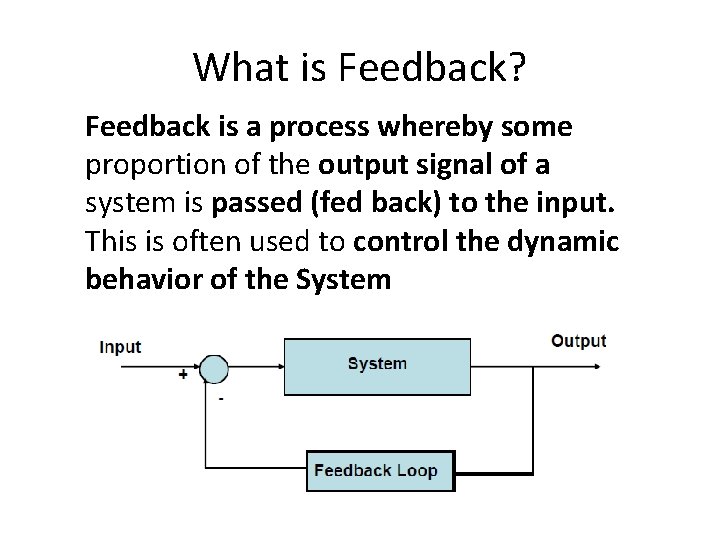
What is Feedback? Feedback is a process whereby some proportion of the output signal of a system is passed (fed back) to the input. This is often used to control the dynamic behavior of the System

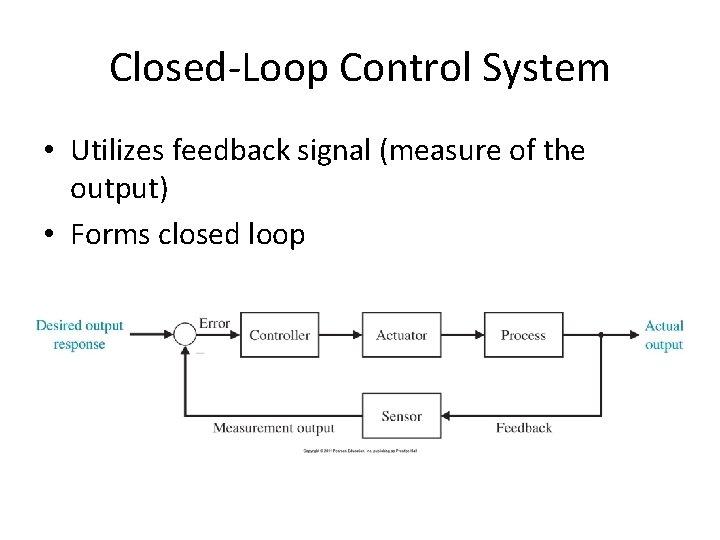
Closed-Loop Control System • Utilizes feedback signal (measure of the output) • Forms closed loop

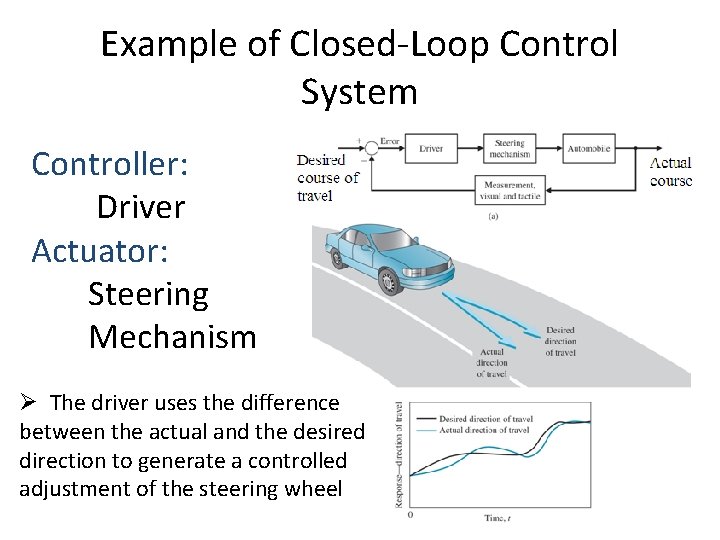
Example of Closed-Loop Control System Controller: Driver Actuator: Steering Mechanism Ø The driver uses the difference between the actual and the desired direction to generate a controlled adjustment of the steering wheel

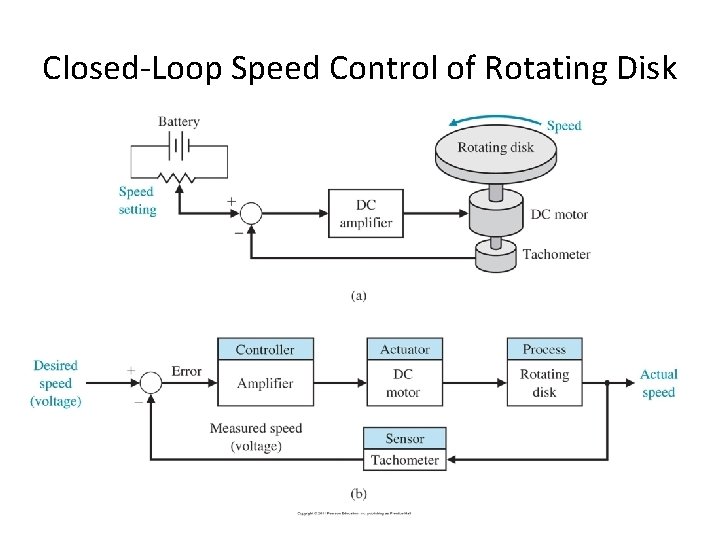
Closed-Loop Speed Control of Rotating Disk

GPS Control

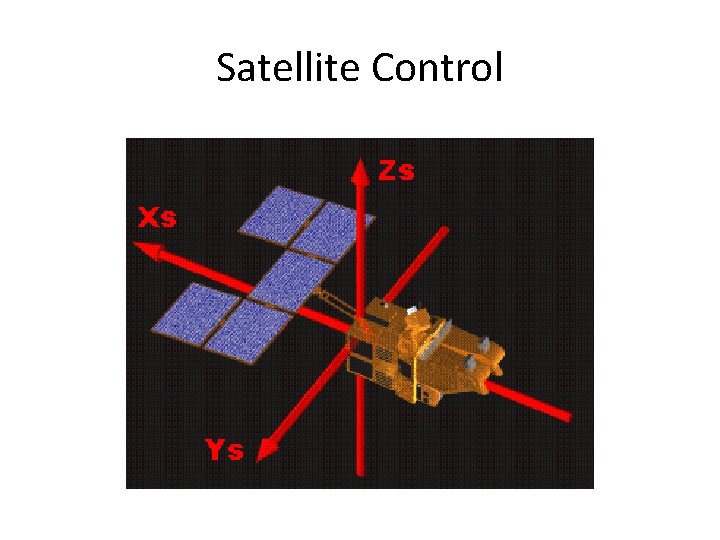
Satellite Control

Satellite Control (Contd…)

Servo Control

Introduction to Scilab • Xcos

Differential Equation N-th order ordinary differential equation Often required to describe physical system ü Higher order equations are difficult to solve directly. ü However, quite easy to solve through Laplace transform. ü

Example of Diff. Equation
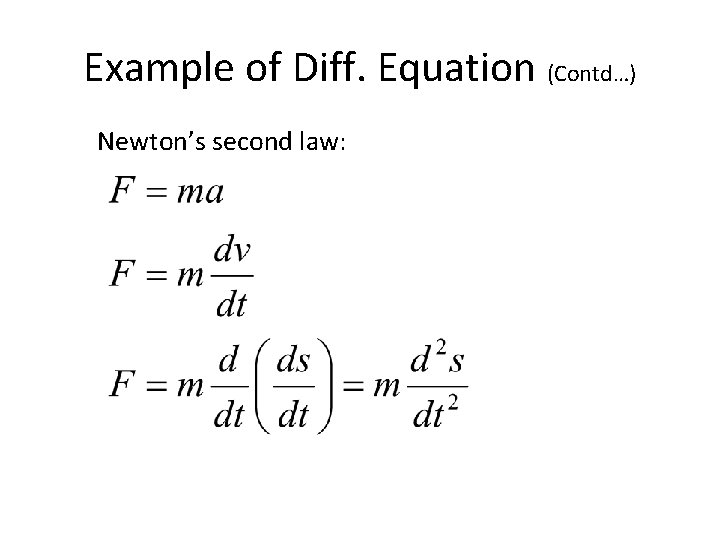
Example of Diff. Equation (Contd…) Newton’s second law:



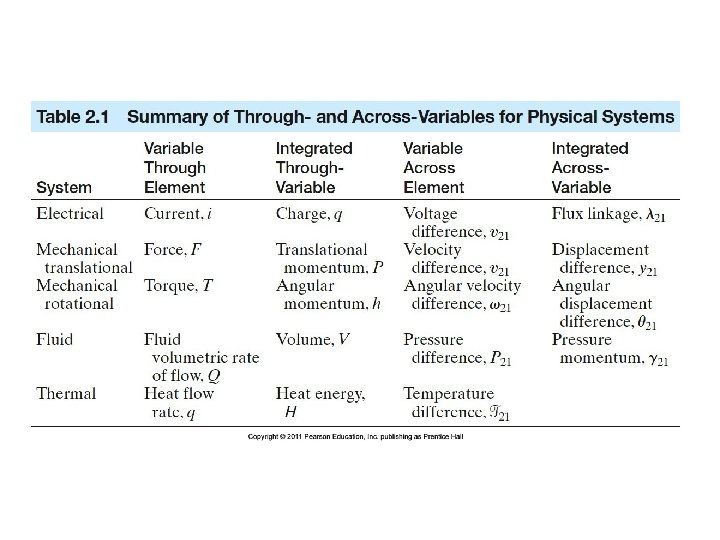
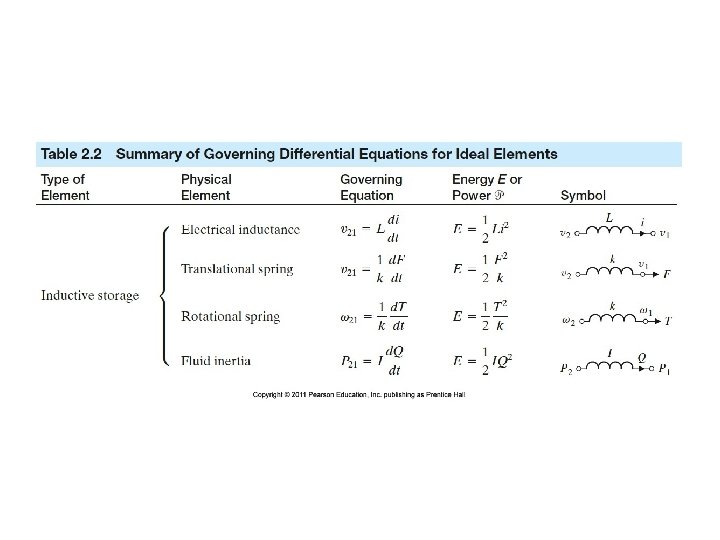
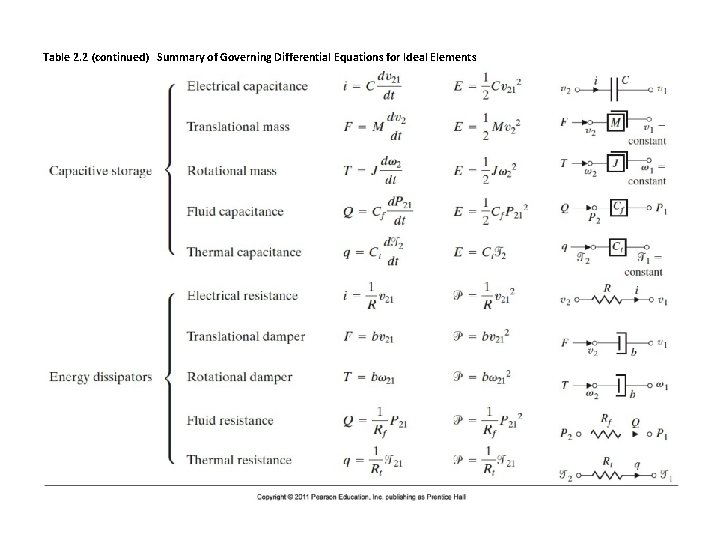
Table 2. 2 (continued) Summary of Governing Differential Equations for Ideal Elements

Laplace Transform • A transformation from time (t) domain to complex frequency (s) domain Ø Laplace Transform is given by

Laplace Transform (contd…) • Example: Consider the step function. u(t) = 1 for t >= 0 u(t) = 0 for t < 0 1 0 -1 t

Inverse Laplace Transform • Transformation from s-domain back to t-domain Inverse Laplace Transform is defined as: Where, is a constant

Laplace Transform Pairs • Laplace transform and its inverse are seldom calculated through equations. • Almost always they are calculated using lookup tables.

Laplace Transform’s table for common functions Function, Unit Impulse, Unit step, Unit ramp, Exponential, Sine, Cosain, Damped sine, Damped cosain, Damped ramp, Laplace Transform 1

Characteristic of Laplace Transform (1) Linear If and are constant and are Laplace Transforms and

Characteristic of Laplace Transform (contd…) (2) Differential Theorem Let and For higher order systems where

Characteristic of Laplace Transform (contd…) (3) Integration Theorem Let is the initial value of the function. where (4) Initial value Theorem Initial value means , thus and as the frequency is inversed of time, this implies that

Characteristic of Laplace Transform (contd…) (5) Final value Theorem In this respect as , gives Example 1 Consider a second order Using differential property and assume intial condition is zero Rearrangge Inverse Lapalce

Example 2 Assume, 0 initial conditions. Taking Laplace transform, we obtain

Example 2 (contd…)

Example 2 (contd…) From table, inverse Laplace transform is Thus the solution of the differential equation

Example 3 Non zero initial condition

Example 3 (contd…)

Example 4 (a) Show that is a solution to the following differential equation (b) Find solution to the above equation using Laplace transform with the following initial condition.

Solution (a)

Solution (b)