17 SECONDORDER DIFFERENTIAL EQUATIONS SECONDORDER DIFFERENTIAL EQUATIONS Secondorder










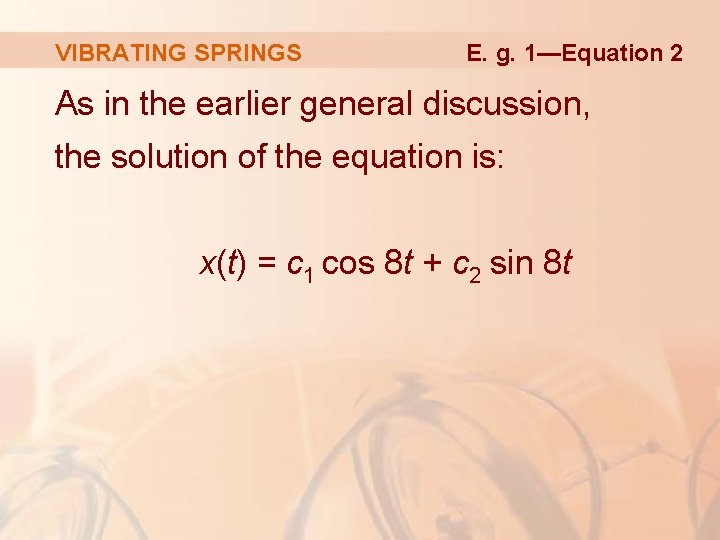

















































- Slides: 68

17 SECOND-ORDER DIFFERENTIAL EQUATIONS

SECOND-ORDER DIFFERENTIAL EQUATIONS Second-order linear differential equations have a variety of applications in science and engineering.

SECOND-ORDER DIFFERENTIAL EQUATIONS 17. 3 Applications of Second-Order Differential Equations In this section, we will learn how: Second-order differential equations are applied to the vibration of springs and electric circuits.

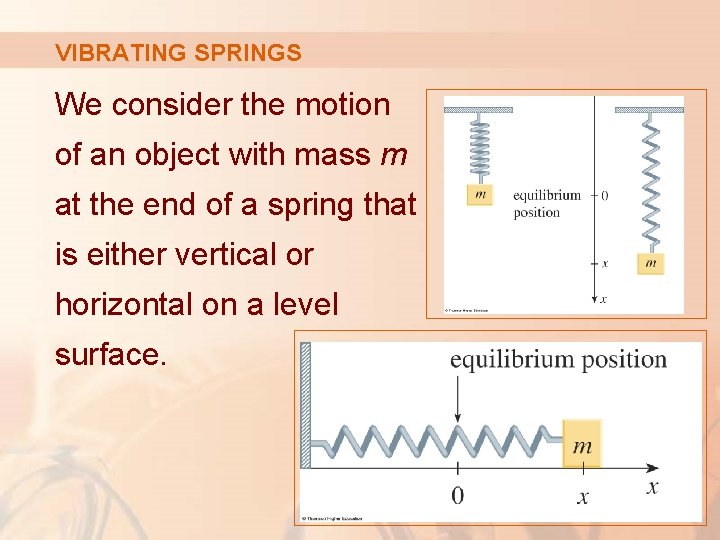
VIBRATING SPRINGS We consider the motion of an object with mass m at the end of a spring that is either vertical or horizontal on a level surface.

SPRING CONSTANT In Section 6. 4, we discussed Hooke’s Law: § If the spring is stretched (or compressed) x units from its natural length, it exerts a force that is proportional to x: restoring force = –kx where k is a positive constant, called the spring constant.

SPRING CONSTANT Equation 1 If we ignore any external resisting forces (due to air resistance or friction) then, by Newton’s Second Law, we have: § This is a second-order linear differential equation.

SPRING CONSTANT Its auxiliary equation is mr 2 + k = 0 with roots r = ±ωi, where Thus, the general solution is: x(t) = c 1 cos ωt + c 2 sin ωt

SIMPLE HARMONIC MOTION This can also be written as x(t) = A cos(ωt + δ) where: § This is called simple harmonic motion.

VIBRATING SPRINGS Example 1 A spring with a mass of 2 kg has natural length 0. 5 m. A force of 25. 6 N is required to maintain it stretched to a length of 0. 7 m. § If the spring is stretched to a length of 0. 7 m and then released with initial velocity 0, find the position of the mass at any time t.

VIBRATING SPRINGS Example 1 From Hooke’s Law, the force required to stretch the spring is: k(0. 25) = 25. 6 Hence, k = 25. 6/0. 2 = 128

VIBRATING SPRINGS Example 1 Using that value of the spring constant k, together with m = 2 in Equation 1, we have:
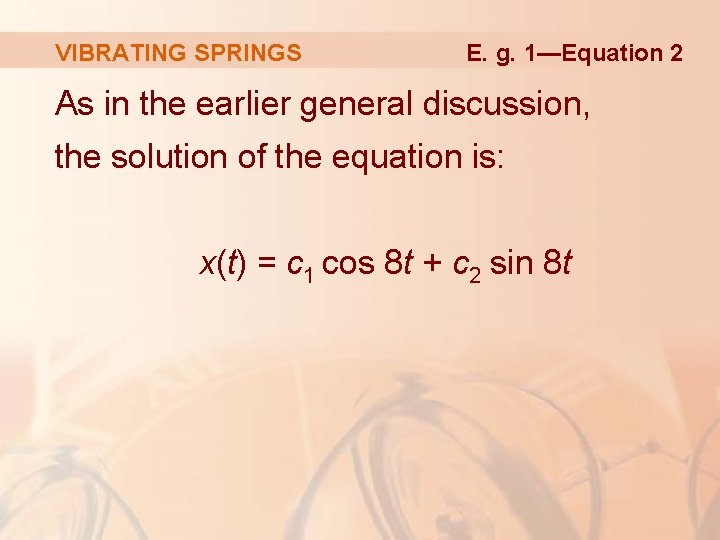
VIBRATING SPRINGS E. g. 1—Equation 2 As in the earlier general discussion, the solution of the equation is: x(t) = c 1 cos 8 t + c 2 sin 8 t

VIBRATING SPRINGS Example 1 We are given the initial condition: x(0) = 0. 2 § However, from Equation 2, x(0) = c 1 § Therefore, c 1 = 0. 2

VIBRATING SPRINGS Example 1 Differentiating Equation 2, we get: x’(t) = – 8 c 1 sin 8 t + 8 c 2 cos 8 t § Since the initial velocity is given as x’(0) = 0, we have c 2 = 0. § So, the solution is: x(t) = (1/5) cos 8 t

DAMPED VIBRATIONS Now, we consider the motion of a spring that is subject to either: § A frictional force (the horizontal spring here) § A damping force (where a vertical spring moves through a fluid, as here)

DAMPING FORCE An example is the damping force supplied by a shock absorber in a car or a bicycle.

DAMPING FORCE We assume that the damping force is proportional to the velocity of the mass and acts in the direction opposite to the motion. § This has been confirmed, at least approximately, by some physical experiments.

DAMPING CONSTANT Thus, where c is a positive constant, called the damping constant.

DAMPED VIBRATIONS Equation 3 Thus, in this case, Newton’s Second Law gives: or

DAMPED VIBRATIONS Equation 4 Equation 3 is a second-order linear differential equation. Its auxiliary equation is: mr 2 + cr + k = 0

DAMPED VIBRATIONS Equation 4 The roots are: § According to Section 17. 1, we need to discuss three cases.

CASE I—OVERDAMPING 2 c – 4 mk > 0 § r 1 and r 2 are distinct real roots. § x = c 1 er 1 t + c 2 er 2 t

CASE I—OVERDAMPING Since c, m, and k are all positive, we have: § So, the roots r 1 and r 2 given by Equations 4 must both be negative. § This shows that x → 0 as t → ∞.

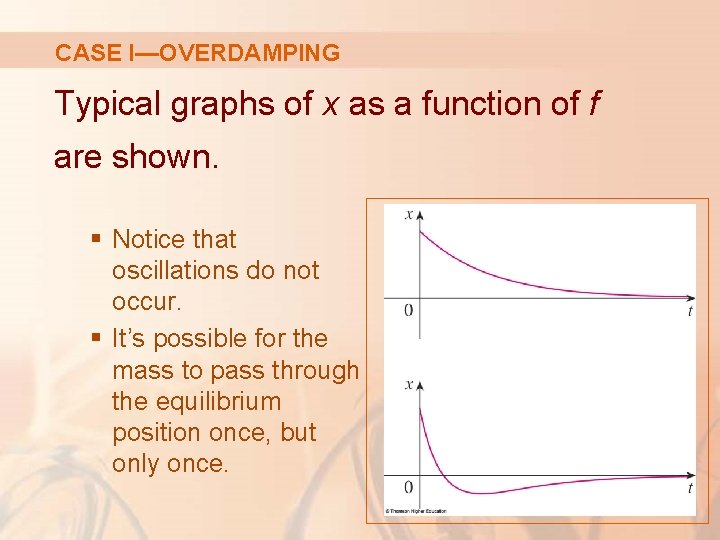
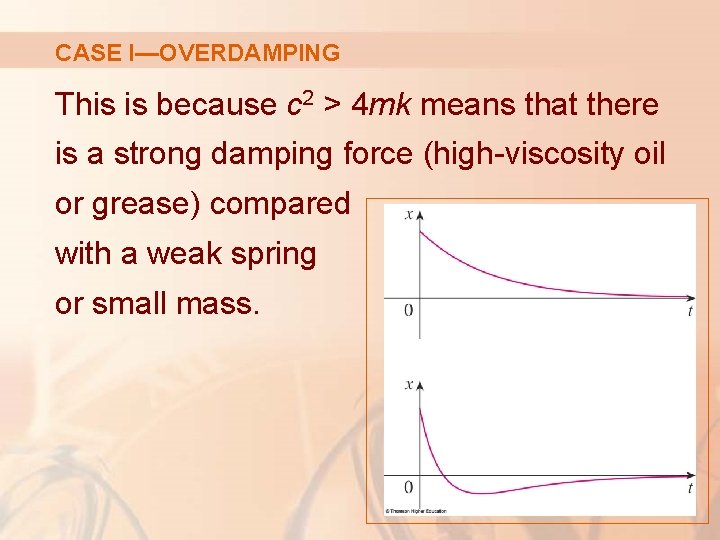
CASE I—OVERDAMPING Typical graphs of x as a function of f are shown. § Notice that oscillations do not occur. § It’s possible for the mass to pass through the equilibrium position once, but only once.

CASE I—OVERDAMPING This is because c 2 > 4 mk means that there is a strong damping force (high-viscosity oil or grease) compared with a weak spring or small mass.

CASE II—CRITICAL DAMPING 2 c – 4 mk = 0 § This case corresponds to equal roots § The solution is given by: x = (c 1 + c 2 t)e–(c/2 m)t

CASE II—CRITICAL DAMPING It is similar to Case I, and typical graphs resemble those in the previous figure. § Still, the damping is just sufficient to suppress vibrations. § Any decrease in the viscosity of the fluid leads to the vibrations of the following case.

CASE III—UNDERDAMPING 2 c – 4 mk < 0 § Here, the roots are complex: where § The solution is given by: x = e–(c/2 m)t(c 1 cos ωt + c 2 sin ωt)

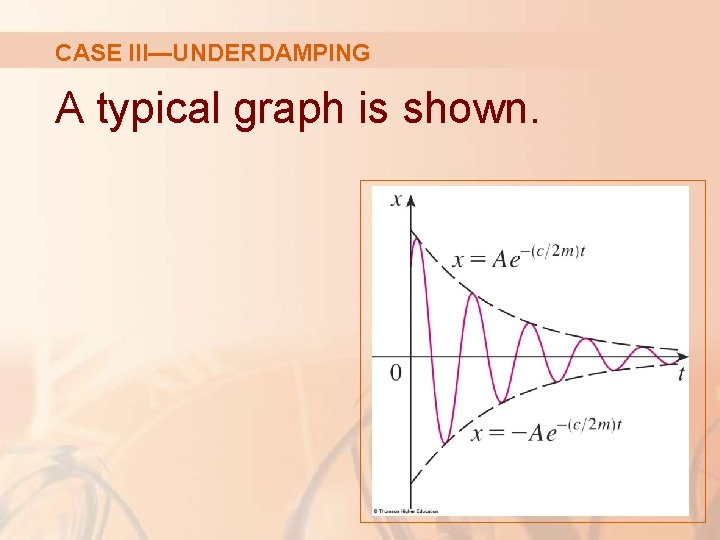
CASE III—UNDERDAMPING We see that there are oscillations that are damped by the factor e–(c/2 m)t. § Since c > 0 and m > 0, we have –(c/2 m) < 0. So, e–(c/2 m)t → 0 as t → ∞. § This implies that x → 0 as t → ∞. That is, the motion decays to 0 as time increases.

CASE III—UNDERDAMPING A typical graph is shown.

DAMPED VIBRATIONS Example 2 Suppose that the spring of Example 1 is immersed in a fluid with damping constant c = 40. § Find the position of the mass at any time t if it starts from the equilibrium position and is given a push to start it with an initial velocity of 0. 6 m/s.

DAMPED VIBRATIONS Example 2 From Example 1, the mass is m = 2 and the spring constant is k = 128. § So, the differential equation 3 becomes: or

DAMPED VIBRATIONS Example 2 The auxiliary equation is: r 2 + 20 r + 64 = (r + 4)(r + 16) = 0 with roots – 4 and – 16. § So, the motion is overdamped, and the solution is: x(t) = c 1 e– 4 t + c 2 e– 16 t

DAMPED VIBRATIONS Example 2 We are given that x(0) = 0. So, c 1 + c 2 = 0. § Differentiating, we get: x’(t) = – 4 c 1 e– 4 t – 16 c 2 e– 16 t § Thus, x’(0) = – 4 c 1 – 16 c 2 = 0. 6

DAMPED VIBRATIONS Example 2 Since c 2 = –c 1, this gives: 12 c 1 = 0. 6 or c 1 = 0. 05 § Therefore, x = 0. 05(e– 4 t – e– 16 t)

FORCED VIBRATIONS Suppose that, in addition to the restoring force and the damping force, the motion of the spring is affected by an external force F(t).

FORCED VIBRATIONS Then, Newton’s Second Law gives:

FORCED VIBRATIONS Equation 5 So, instead of the homogeneous equation 3, the motion of the spring is now governed by the following non-homogeneous differential equation: § The motion of the spring can be determined by the methods of Section 17. 2

PERIOD FORCE FUNCTION A commonly occurring type of external force is a periodic force function F(t) = F 0 cos ω0 t where ω0 ≠ ω =

PERIOD FORCE FUNCTION Equation 6 In this case, and in the absence of a damping force (c = 0), you are asked in Exercise 9 to use the method of undetermined coefficients to show that:

RESONANCE If ω0 = ω, then the applied frequency reinforces the natural frequency and the result is vibrations of large amplitude. This is the phenomenon of resonance. § See Exercise 10.

ELECTRIC CIRCUITS In Sections 9. 3 and 9. 5, we were able to use first-order separable and linear equations to analyze electric circuits that contain a resistor and inductor or a resistor and capacitor.

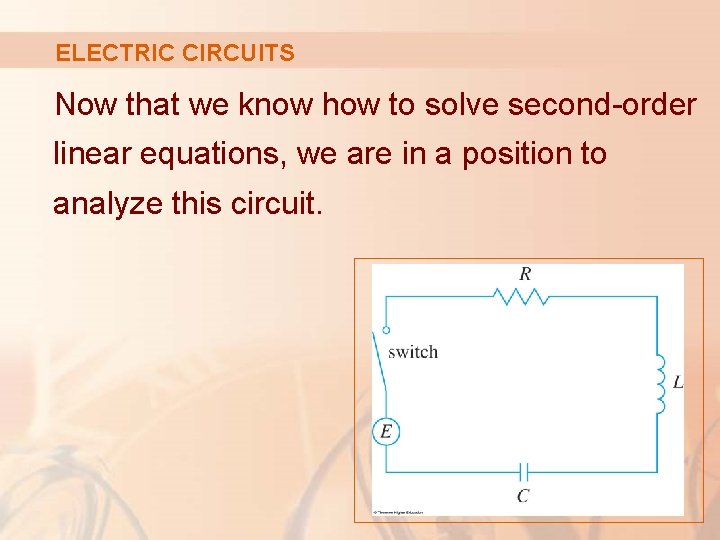
ELECTRIC CIRCUITS Now that we know how to solve second-order linear equations, we are in a position to analyze this circuit.

ELECTRIC CIRCUITS It contains in series: § An electromotive force E (supplied by a battery or generator) § A resistor R § An inductor L § A capacitor C

ELECTRIC CIRCUITS If the charge on the capacitor at time t is Q = Q(t), then the current is the rate of change of Q with respect to t: I = d. Q/dt

ELECTRIC CIRCUITS As in Section 9. 5, it is known from physics that the voltage drops across the resistor, inductor, and capacitor, respectively, are:

ELECTRIC CIRCUITS Kirchhoff’s voltage law says that the sum of these voltage drops is equal to the supplied voltage:

ELECTRIC CIRCUITS Equation 7 Since I = d. Q/dt, the equation becomes: § This is a second-order linear differential equation with constant coefficients.

ELECTRIC CIRCUITS If the charge Q 0 and the current I 0 are known at time 0, then we have the initial conditions: Q(0) = Q 0 Q’(0) = I 0 § Then, the initial-value problem can be solved by the methods of Section 17. 2

ELECTRIC CIRCUITS A differential equation for the current can be obtained by differentiating Equation 7 with respect to t and remembering that I = d. Q/dt:

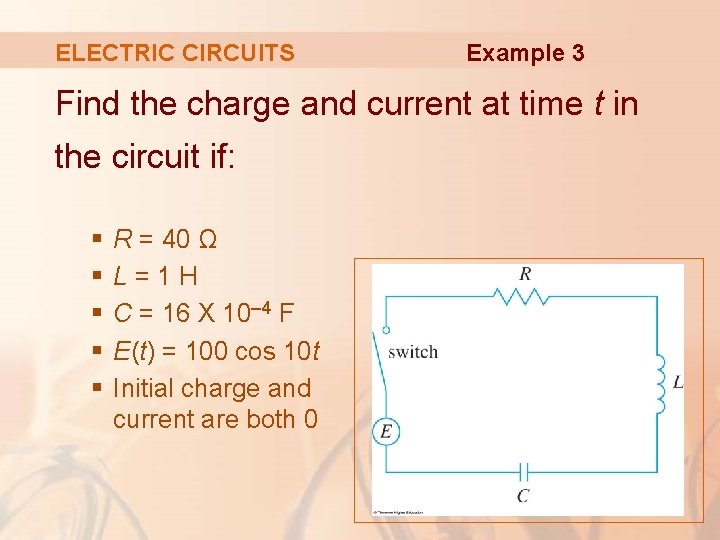
ELECTRIC CIRCUITS Example 3 Find the charge and current at time t in the circuit if: § § § R = 40 Ω L=1 H C = 16 X 10– 4 F E(t) = 100 cos 10 t Initial charge and current are both 0

ELECTRIC CIRCUITS E. g. 3—Equation 8 With the given values of L, R, C, and E(t), Equation 7 becomes:

ELECTRIC CIRCUITS Example 3 The auxiliary equation is r 2 + 40 r + 625 = 0 with roots § So, the solution of the complementary equation is: Qc(t) = e– 20 t(c 1 cos 15 t + c 2 sin 15 t)

ELECTRIC CIRCUITS Example 3 For the method of undetermined coefficients, we try the particular solution Qp(t) = A cos 10 t + B sin 10 t § Then, Qp’ (t) = – 10 A sin 10 t + 10 B cos 10 t Qp’’(t) = – 100 A cos 10 t – 100 B sin 10 t

ELECTRIC CIRCUITS Example 3 Substituting into Equation 8, we have: § (– 100 A cos 10 t – 100 B sin 10 t) + 40(– 10 A sin 10 t + 10 B cos 10 t) + 625(A cos 10 t + B sin 10 t) = 100 cos 10 t or (525 A + 400 B) cos 10 t + (– 400 A + 525 B) sin 10 t = 100 cos 10 t

ELECTRIC CIRCUITS Example 3 Equating coefficients, we have: 525 A + 400 B = 100 – 400 A + 525 B = 0 or 21 A + 16 B = 4 § The solution is: – 16 A + 21 B = 0 ,

ELECTRIC CIRCUITS So, a particular solution is: The general solution is: Example 3

ELECTRIC CIRCUITS Example 3 Imposing the initial condition Q(0), we get:

ELECTRIC CIRCUITS Example 3 To impose the other initial condition, we first differentiate to find the current:

ELECTRIC CIRCUITS Thus, Example 3

ELECTRIC CIRCUITS Example 3 So, the formula for the charge is:

ELECTRIC CIRCUITS Example 3 The expression for the current is:

NOTE 1 In Example 3, the solution for Q(t) consists of two parts. § Since e– 20 t → 0 as t → ∞ and both cos 15 t and sin 15 t are bounded functions,

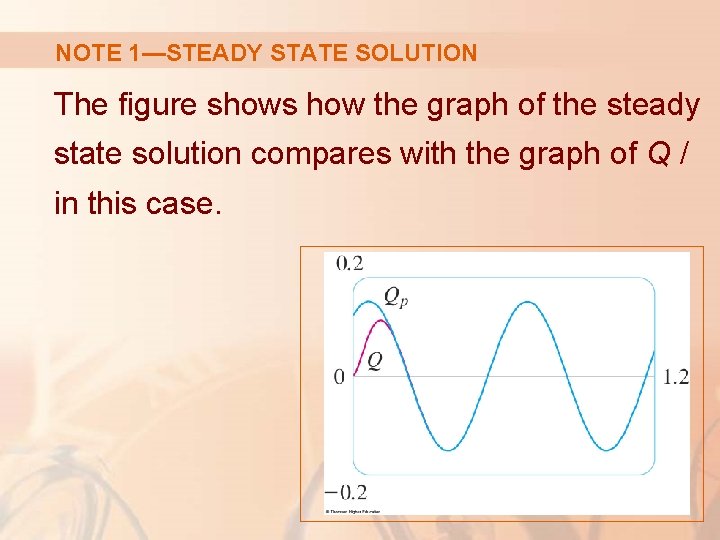
NOTE 1—STEADY STATE SOLUTION So, for large values of t, § For this reason, Qp(t) is called the steady state solution.

NOTE 1—STEADY STATE SOLUTION The figure shows how the graph of the steady state solution compares with the graph of Q / in this case.

NOTE 2 Comparing Equations 5 and 7, we see that, mathematically, they are identical.

NOTE 2 This suggests the analogies given in the following chart between physical situations that, at first glance, are very different.

NOTE 2 We can also transfer other ideas from one situation to the other. For instance, § The steady state solution discussed in Note 1 makes sense in the spring system. § The phenomenon of resonance in the spring system can be usefully carried over to electric circuits as electrical resonance.