UNIVERSITI MALAYSIA PERLIS EKT 2414 ELECTROMAGNETIC THEORY CHAPTER


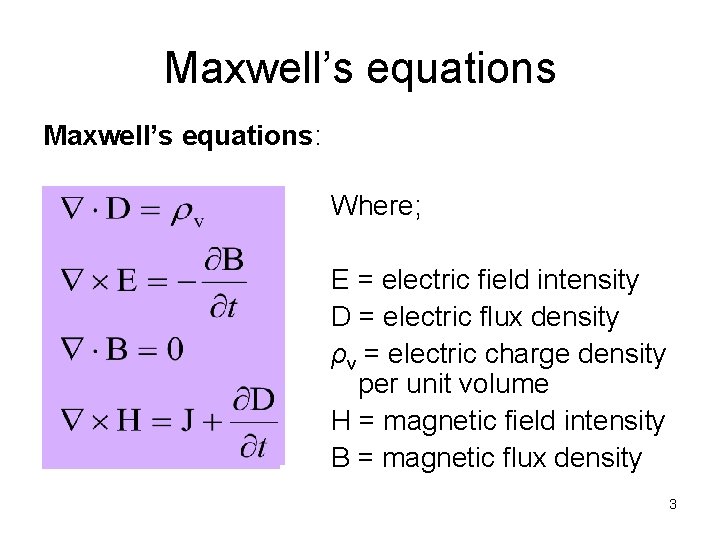

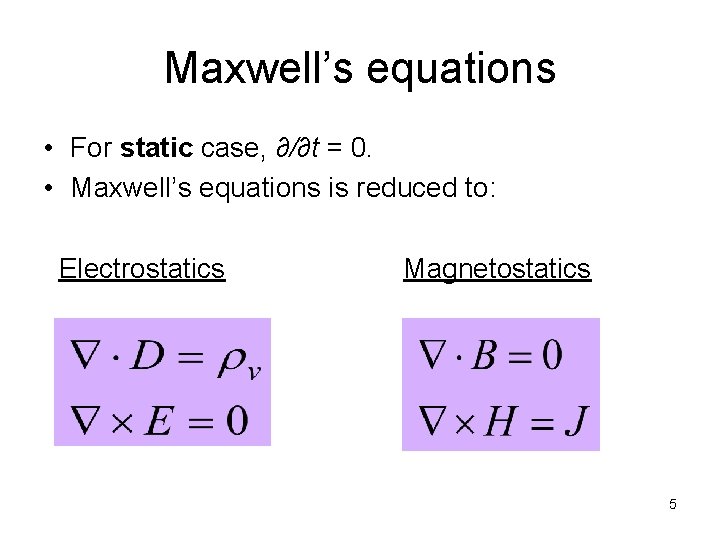






















































- Slides: 83

UNIVERSITI MALAYSIA PERLIS EKT 241/4: ELECTROMAGNETIC THEORY CHAPTER 3 – ELECTROSTATICS 1

Chapter Outline § § § Maxwell’s Equations Charge and Current Distributions Coulomb’s Law Gauss’s Law Electric Scalar Potential Electrical Properties of Materials Conductors & Dielectrics Electric Boundary Conditions Capacitance Electrostatic Potential Energy Image Method 2
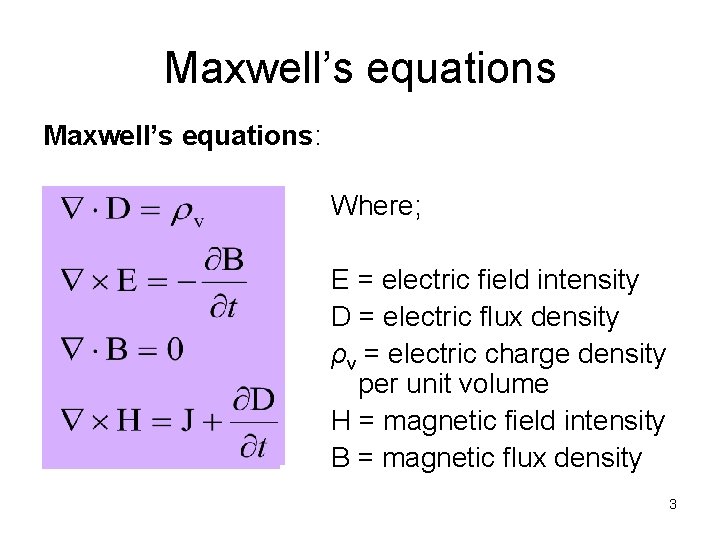
Maxwell’s equations: Where; E = electric field intensity D = electric flux density ρv = electric charge density per unit volume H = magnetic field intensity B = magnetic flux density 3

Maxwell’s equations: Relationship: D=εE B=µH ε = µ = electrical permittivity of the material magnetic permeability of the material 4
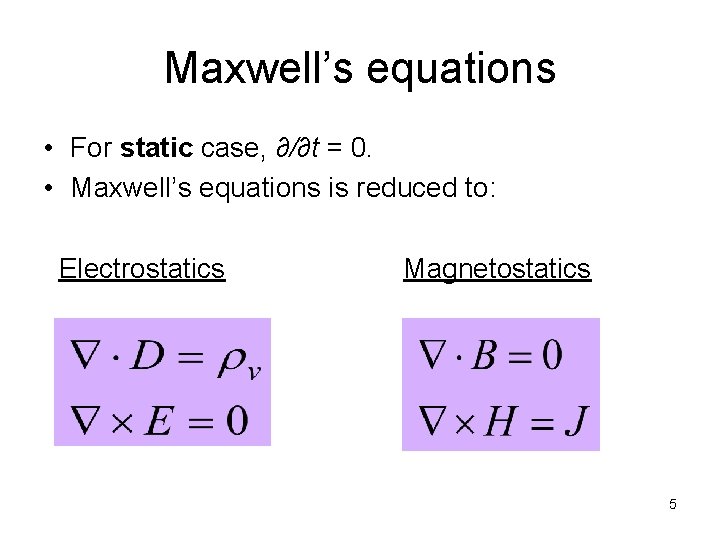
Maxwell’s equations • For static case, ∂/∂t = 0. • Maxwell’s equations is reduced to: Electrostatics Magnetostatics 5

Charge and current distributions § Charge may be distributed over a volume, a surface or a line. § Electric field due to continuous charge distributions: 6

Charge and current distributions §Volume charge density, ρv is defined as: §Total charge Q contained in a volume V is: 7

Charge and current distributions • Surface charge density • Total charge Q on a surface: 8

Charge and current distributions • Line charge density • Total charge Q along a line 9

Example 1 Calculate the total charge Q contained in a cylindrical tube of charge oriented along the zaxis. The line charge density is , where z is the distance in meters from the bottom end of the tube. The tube length is 10 cm. 10

Solution to Example 1 The total charge Q is: 11

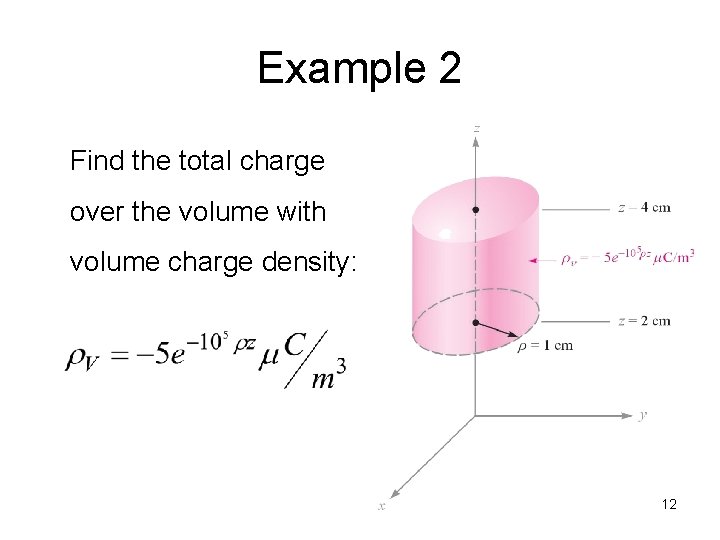
Example 2 Find the total charge over the volume with volume charge density: 12

Solution to Example 2 The total charge Q: 13

Current densities • Current density, J is defined as: • Where: u = mean velocity of moving charges • For surface S, total current flowing through is 14

Current densities • There are 2 types of current: 1) Convection current § generated by actual movement of electrically charged matter; does NOT obey Ohm’s law § E. g movement of charged particles in cathode ray tube 2) Conduction current § atoms of conducting material do NOT move; obeys Ohm’s law § E. g movement of electrons in a metal wire 15

Coulomb’s Law Coulomb’s law for a point charge: Where; R = distance between P and q = unit vector from q to P ε = electrical permittivity of the medium containing the observation point P 16

Force acting on a charge • In the presence of an electric field E at a given point in space, • F is the force acting on a test charge q’ when that charge is placed at that given point in space • The electric field E is maybe due to a single charge or a distribution of many charges Units: F in Newtons (N), q’ in Coulombs (C) 17

For acting on a charge § For a material with electrical permittivity, ε: D=εE where: ε = εR ε 0 = 8. 85 × 10− 12 ≈ (1/36π) × 10− 9 (F/m) § For most material and under most condition, ε is constant, independent of the magnitude and direction of E 18

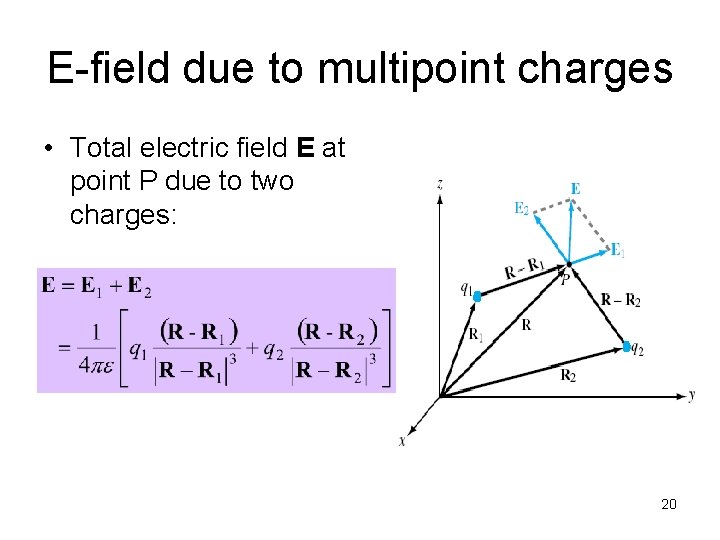
E-field due to multipoint charges • At point P, the electric field E 1 due to q 1 alone: • At point P, the electric field E 1 due to q 2 alone: 19

E-field due to multipoint charges • Total electric field E at point P due to two charges: 20

E-field due to multipoint charges • In general for case of N point of charges, 21

Example 3 Two point charges with and are located in free space at (1, 3, − 1) and (− 3, 1, − 2), respectively in a Cartesian coordinate system. Find: (a) the electric field E at (3, 1, − 2) (b) the force on a 8 × 10− 5 C charge located at that point. All distances are in meters. 22

Solution to Example 3 • The electric field E with ε = ε 0 (free space) is given by: • The vectors are: 23

Solution to Example 3 • a) Hence, • b) We have 24

E-field due to charge distribution continuous distribution • Total electric field due to 3 types of continuous charge distribution: 25

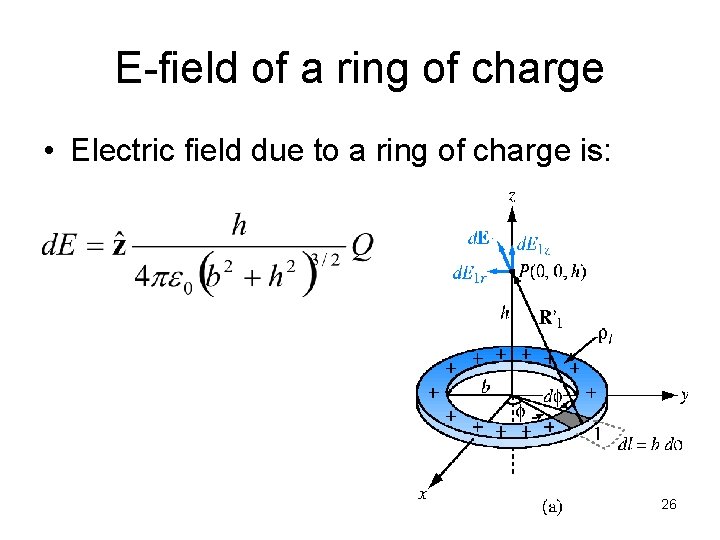
E-field of a ring of charge • Electric field due to a ring of charge is: 26

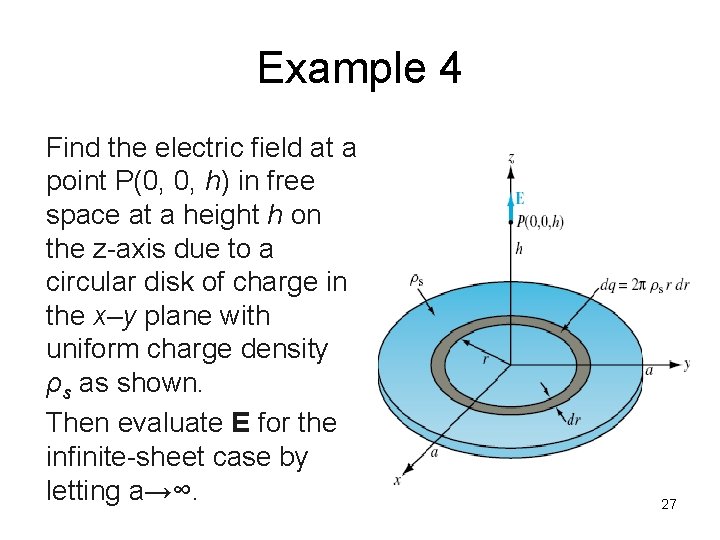
Example 4 Find the electric field at a point P(0, 0, h) in free space at a height h on the z-axis due to a circular disk of charge in the x–y plane with uniform charge density ρs as shown. Then evaluate E for the infinite-sheet case by letting a→∞. 27

Solution to Example 4 • A ring of radius r and width dr has an area ds = 2πrdr • The charge is: • The field due to the ring is: 28

Solution to Example 4 stop • The total electric field at P is With plus sign corresponds to h>0, minus sign corresponds to h<0. • For an infinite sheet of charge with a =∞, 29

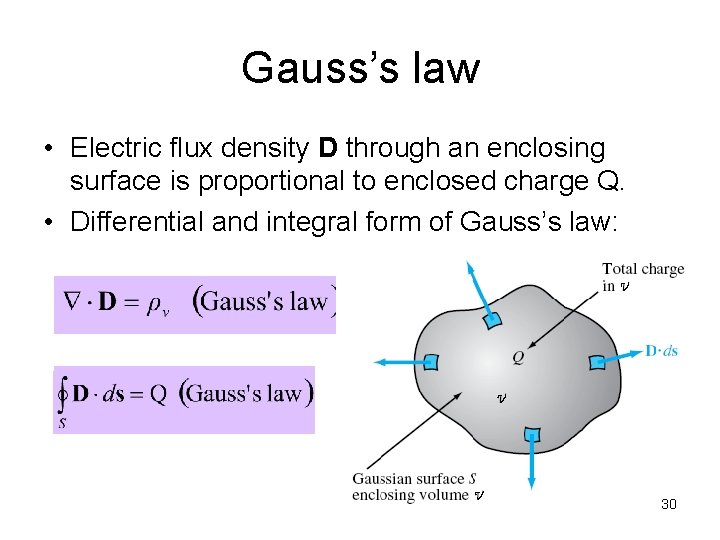
Gauss’s law • Electric flux density D through an enclosing surface is proportional to enclosed charge Q. • Differential and integral form of Gauss’s law: 30

Example 5 • Use Gauss’s law to obtain an expression for E in free space due to an infinitely long line of charge with uniform charge density ρl along the z-axis. 31

Solution to Example 5 Construct a cylindrical Gaussian surface. The integral is: Equating both equations, and re-arrange, we get: 32

Solution to Example 5 Then, use , we get: Note: unit vector is inserted for E due to the fact that E is a vector in direction. For application example refer to tutorial 2 33

Electric scalar potential • Electric potential energy is required to move a unit charge between 2 points • The presence of an electric field between two points give rise to voltage difference 34

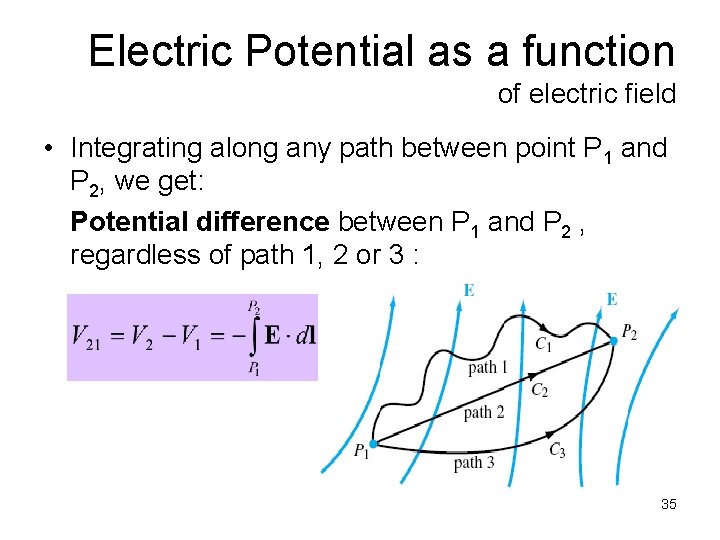
Electric Potential as a function of electric field • Integrating along any path between point P 1 and P 2, we get: Potential difference between P 1 and P 2 , regardless of path 1, 2 or 3 : 35

Electric Potential as a function of electric field • Kirchhoff’s voltage law states that the net voltage drop around a closed loop is zero. • Line integral E around closed contour C is: • The electric potential V at any point is given by: • Integration path between point P 1 and P 2 is arbitrary 36

Electric potential due to point charges • For a point charge located at the origin of a spherical coordinate systems, the electric field at a distance R: • The electric potential between two end points: 37

Electric potential due to point charges • For charge Q located other than origin, specified by a source position vector R 1, then V at the observation vector R becomes: • For N discrete point charges, electric potential is: 38

Electric potential due to continuous distributions • For a continuous charge distribution: 39

Electric field as a function of electric potential • To find E for any charge distribution easily, where: = gradient of V 40

Poisson’s & Laplace’s equations • Differential form of Gauss’s law: • This may be written as: • Then, using , we get: 41

Poisson’s & Laplace’s equations • Hence: • Poisson’s and Laplace’s equations are used to find V where boundaries are known: • Example: the region between the plates of a capacitor with a specified voltage difference across it. (we will see in capacitance topic) 42

Conductivity • Conductivity – characterizes the ease with which charges can move freely in a material. • Perfect dielectric, σ = 0. Charges do not move inside the material • Perfect conductor, σ = ∞. Charges move freely throughout the material 43 •

Conductivity • Drift velocity of electrons, in a conducting material is in the opposite direction to the externally applied electric field E: • Hole drift velocity, is in the same direction as the applied electric field E: where: µe = electron mobility (m 2/V. s) µh = hole mobility (m 2/V. s) 44

Conductivity • Conductivity of a material, σ, is defined as: where ρve = volume charge density of free electrons ρvh = volume charge density of free holes Ne = number of free electrons per unit volume Nh = number of free holes per unit volume e = absolute charge = 1. 6 × 10− 19 (C) 45

Conductivity • Conductivities of different materials: 46

Ohm’s Law stop • Point form of Ohm’s law states that: Where: J = current density σ = conductivity E = electric field intensity • Properties for perfect dielectric and conductor: 47

Example 6 A 2 -mm-diameter copper wire with conductivity of 5. 8 × 107 S/m and electron mobility of 0. 0032 (m 2/V·s) is subjected to an electric field of 20 (m. V/m). Find : The free electron volume charge density and the current density, total current flowing in the wire and the electron drift velocity, and the volume density of the free electrons. 48

Solution to Example 6 a) b) c) d) e) 49

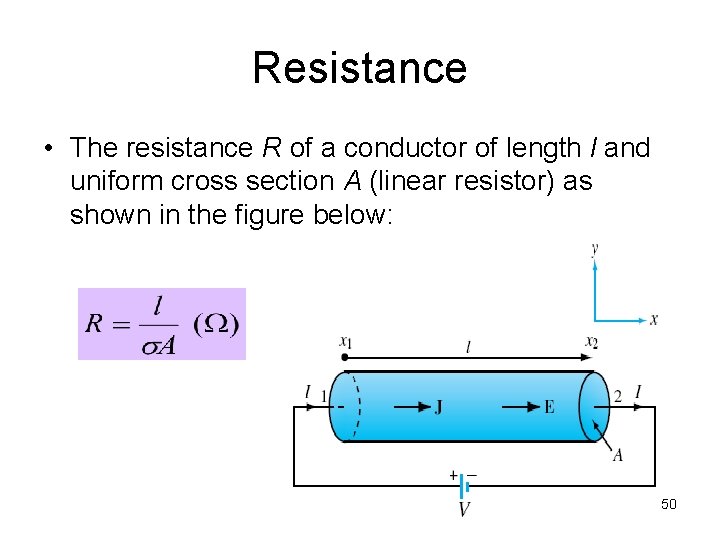
Resistance • The resistance R of a conductor of length l and uniform cross section A (linear resistor) as shown in the figure below: 50

Resistance • For a resistor of arbitrary shape, the resistance R is: • The conductance G of a linear resistor: 51

Joule’s Law • Joule’s law states that for a volume v, the total dissipated power P is: • For a linear resistor, the dissipated power P: 52

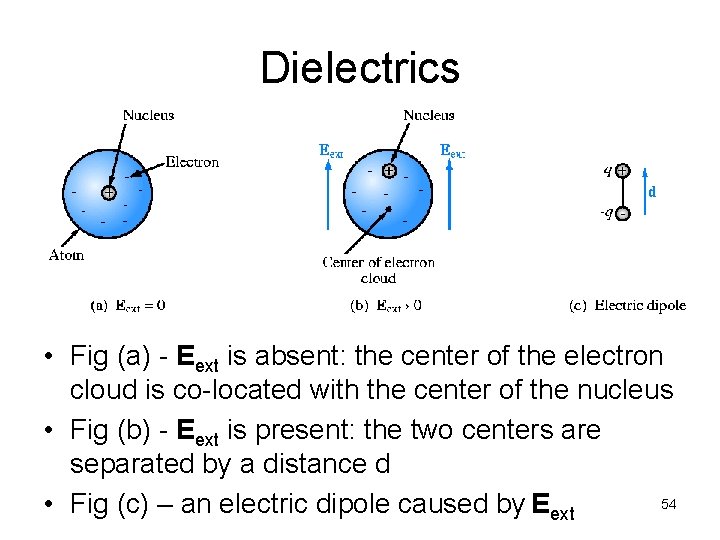
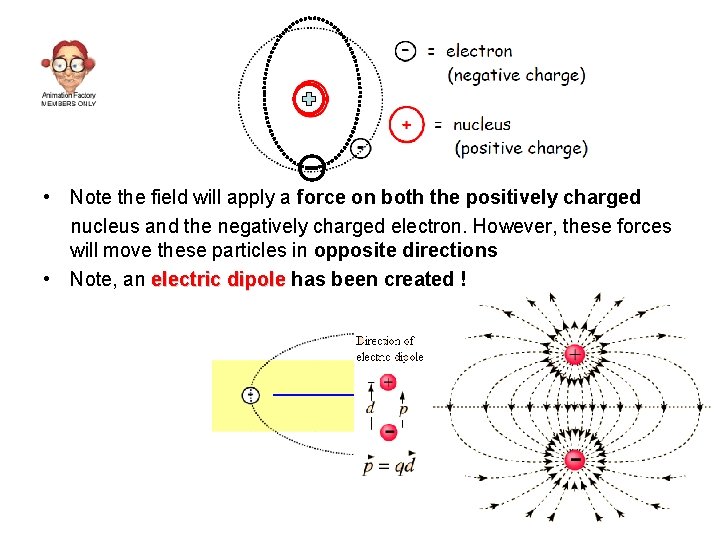
Dielectrics • Conductor has free electrons. • Dielectric electrons are strongly bounded to the atom. • In a dielectric, an externally applied electric field, Eext cannot cause mass migration of charges since none are able to move freely. • But, Eext can polarize the atoms or molecules in the material. • The polarization is represented by an electric dipole. 53

Dielectrics • Fig (a) - Eext is absent: the center of the electron cloud is co-located with the center of the nucleus • Fig (b) - Eext is present: the two centers are separated by a distance d 54 • Fig (c) – an electric dipole caused by Eext

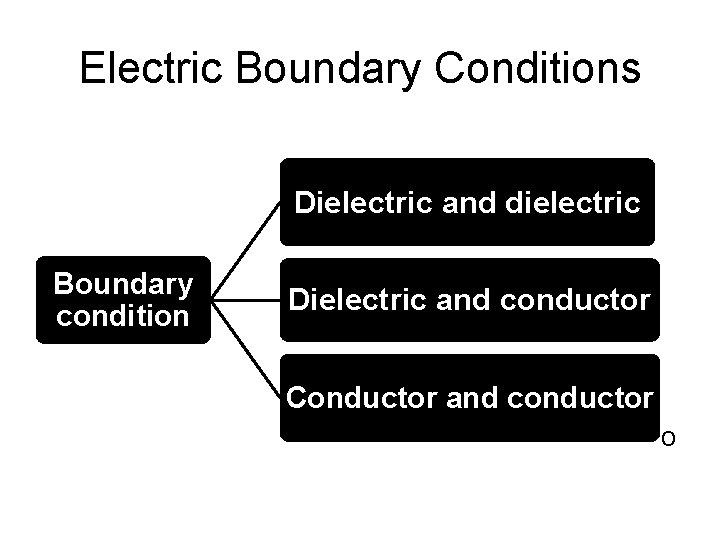
Electric Boundary Conditions • Electric field maybe continuous in each of two dissimilar media • But, the E-field maybe discontinuous at the boundary between them • Boundary conditions specify how the tangential and normal components of the field in one medium are related to the components in other medium across the boundary • Two dissimilar media could be: two different dielectrics, or a conductor and a dielectric, or two conductors 55

• Note the field will apply a force on both the positively charged nucleus and the negatively charged electron. However, these forces will move these particles in opposite directions • Note, an electric dipole has been created !

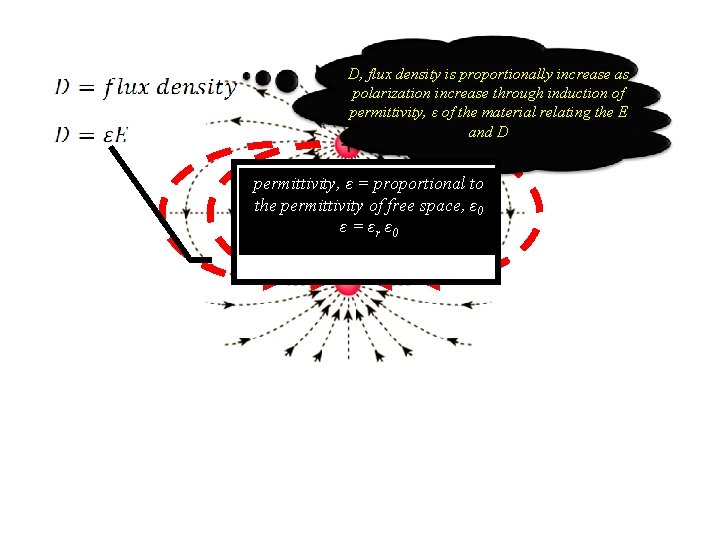
D, flux density is proportionally increase as polarization increase through induction of permittivity, ε of the material relating the E and D permittivity, ε = proportional to the permittivity of free space, ε 0 ε = εr ε 0

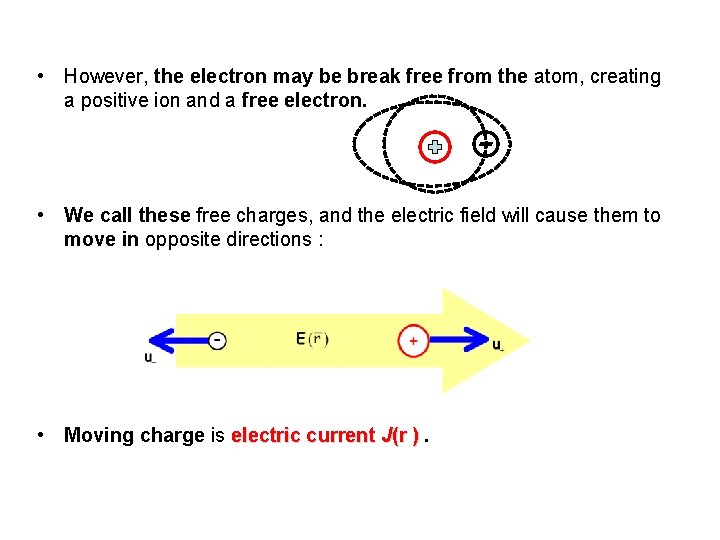
• However, the electron may be break free from the atom, creating a positive ion and a free electron. • We call these free charges, and the electric field will cause them to move in opposite directions : • Moving charge is electric current J(r ).

Electric Boundary Conditions • Electric field maybe continuous in each of two dissimilar media Dielectric and dielectric • But, the E-field maybe discontinuous at the boundary between them • Boundary conditions specify how the tangential Dielectric and conductor and normal components of the field in one condition medium are related to the components in other medium across the boundary Conductor • Two dissimilar media could be: and two conductor different dielectrics, or a conductor and a dielectric, or two conductors

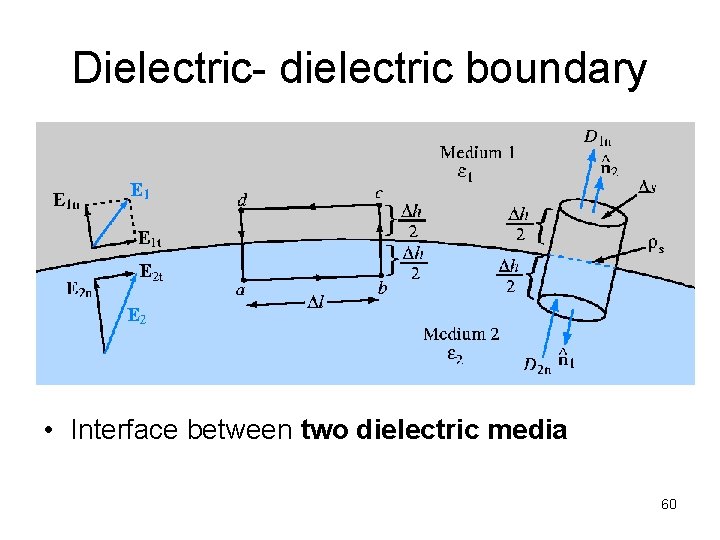
Dielectric- dielectric boundary • Interface between two dielectric media 60

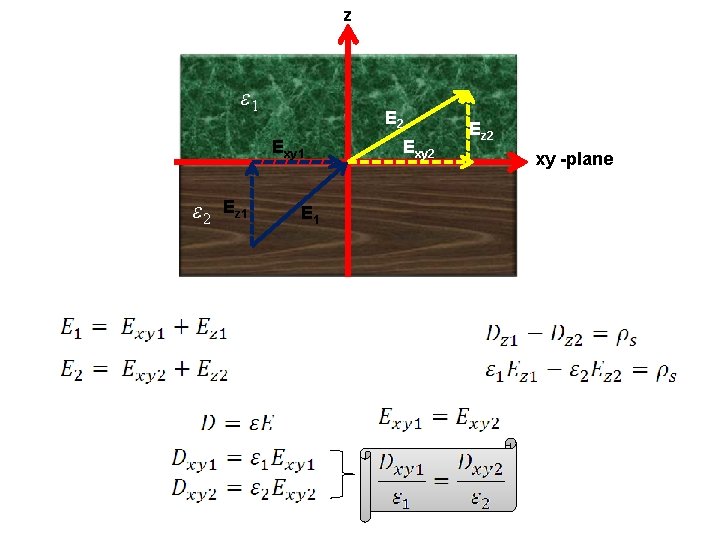
Dielectric- dielectric boundary • Based on the figure in previous slide: • First boundary condition related to the tangential components of the electric field E is: • Second boundary condition related to the normal components of the electric field E is: • OR 61

z ε 1 E 2 Exy 1 ε 2 Ez 1 Exy 2 Ez 2 xy -plane

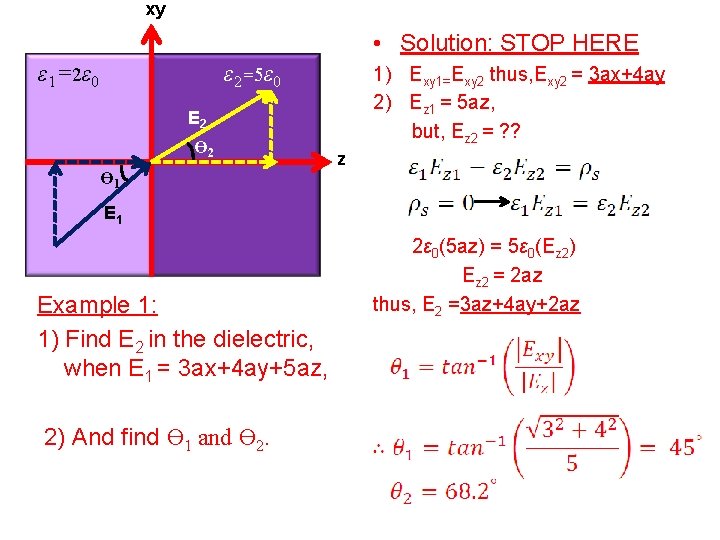
xy • Solution: STOP HERE ε 1=2ε 0 ε 2=5ε 0 1) Exy 1=Exy 2 thus, Exy 2 = 3 ax+4 ay 2) Ez 1 = 5 az, but, Ez 2 = ? ? E 2 Ө 1 z E 1 Example 1: 1) Find E 2 in the dielectric, when E 1 = 3 ax+4 ay+5 az, 2) And find Ө 1 and Ө 2. 2ε 0(5 az) = 5ε 0(Ez 2) Ez 2 = 2 az thus, E 2 =3 az+4 ay+2 az

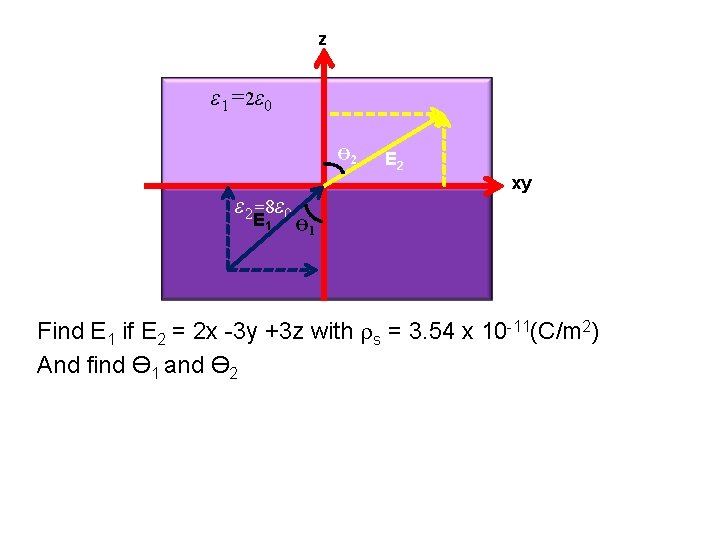
z ε 1=2ε 0 Ө 2 ε 2=8ε 0 E 1 E 2 xy Ө 1 Find E 1 if E 2 = 2 x -3 y +3 z with s = 3. 54 x 10 -11(C/m 2) And find Ө 1 and Ө 2

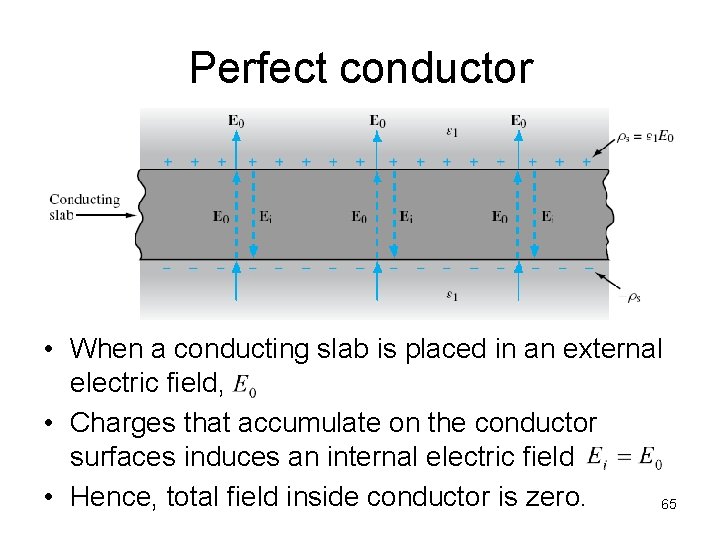
Perfect conductor • When a conducting slab is placed in an external electric field, • Charges that accumulate on the conductor surfaces induces an internal electric field • Hence, total field inside conductor is zero. 65

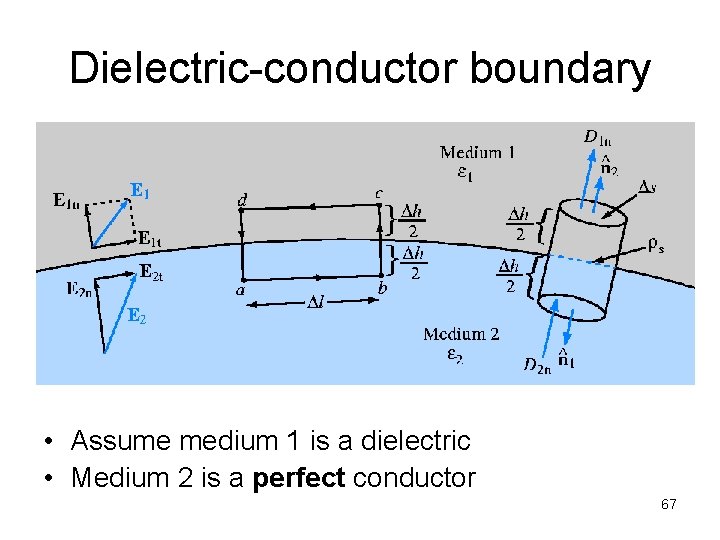
Dielectric-conductor boundary • Based on the figure in previous slide: • In a perfect conductor, • Hence, • This requires the tangential and normal components of E 2 and D 2 to be zero. 66

Dielectric-conductor boundary • Assume medium 1 is a dielectric • Medium 2 is a perfect conductor 67

Dielectric-conductor boundary • The fields in the dielectric medium, at the boundary with the conductor is. • Since , it follows that. • Using the equation, , • we get: • Hence, boundary condition at conductor surface: where = normal vector pointing outward 68

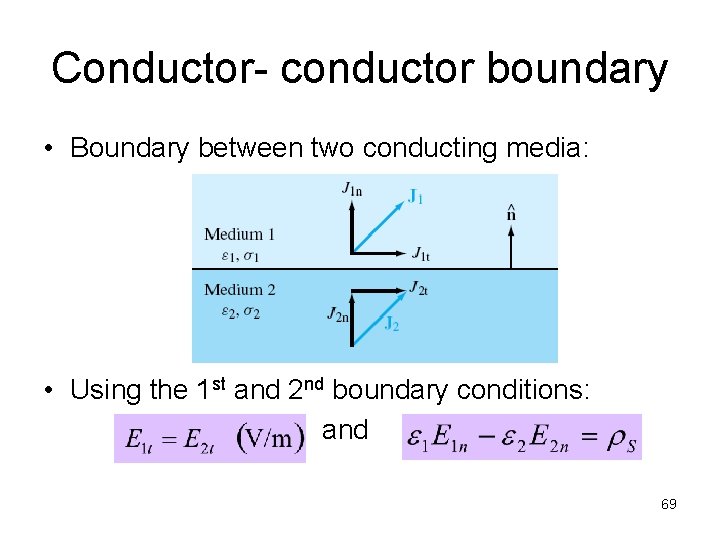
Conductor- conductor boundary • Boundary between two conducting media: • Using the 1 st and 2 nd boundary conditions: and 69

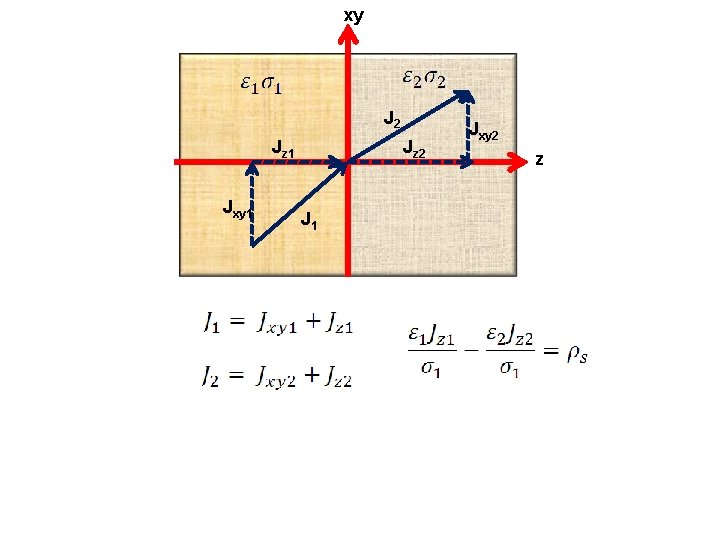
xy J 2 Jz 1 Jxy 1 Jz 2 J 1 Jxy 2 z

Conductor- conductor boundary • In conducting media, electric fields give rise to current densities. • From , we have: and • The normal component of J has be continuous across the boundary between two different media under electrostatic conditions. 71

Conductor- conductor boundary • Hence, upon setting , we found the boundary condition for conductor- conductor boundary: 72

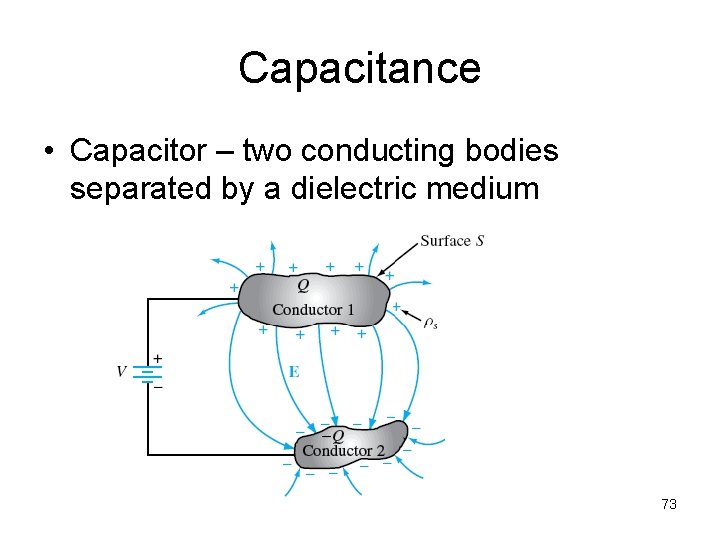
Capacitance • Capacitor – two conducting bodies separated by a dielectric medium 73

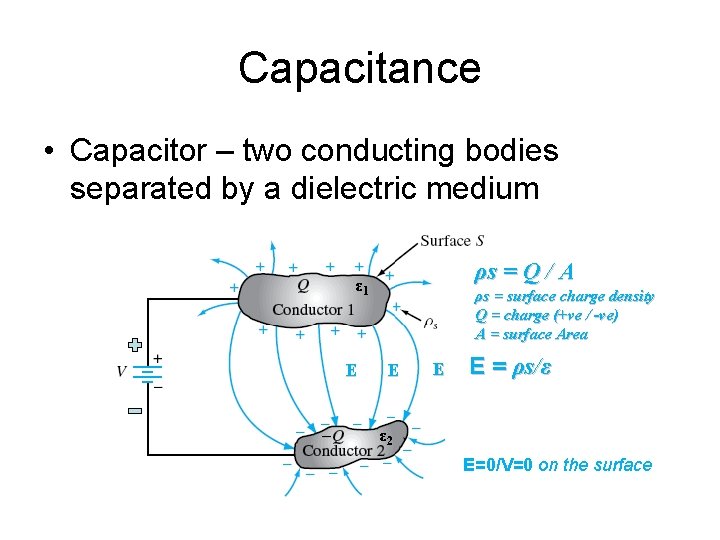
Capacitance • Capacitor – two conducting bodies separated by a dielectric medium ρs = Q / A ε 1 E ρs = surface charge density Q = charge (+ve / -ve) A = surface Area E E E = ρs/ε ε 2 E=0/V=0 on the surface

Capacitance • Capacitance is defined as: where: V = potential difference (V) Q = charge (C) C = capacitance (F) 75

Capacitance • Capacitance is defined as: where: V = potential difference (V) Q = charge (C) C = capacitance (F)

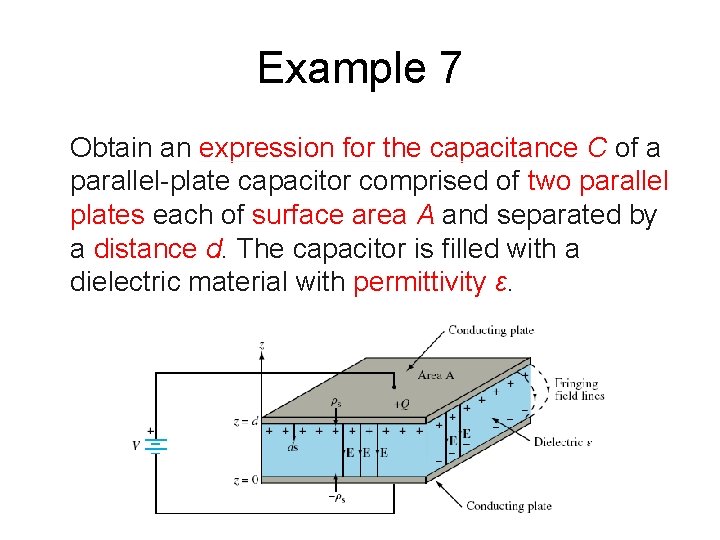
Example 7 Obtain an expression for the capacitance C of a parallel-plate capacitor comprised of two parallel plates each of surface area A and separated by a distance d. The capacitor is filled with a dielectric material with permittivity ε.

Solution to Example 7 • The charge density on the upper plate is ρs = Q/A. Hence, • magnitude of E at the dielectric-conductor boundary: • The voltage difference is • Hence, the capacitance is: 78

Electrostatic potential energy • Assume a capacitor with plates of good conductors – zero resistance, • Dielectric between two conductors has negligible conductivity, σ ≈ 0 – no current can flow through dielectric • No ohmic losses occur anywhere in capacitor • When a source is connected to a capacitor, energy is stored in capacitor • Charging-up energy is stored in the form of electrostatic potential energy in the dielectric medium 79

Electrostatic potential energy • Electrostatic potential energy, • The capacitance: • Hence, We for a parallel plate capacitor: 80

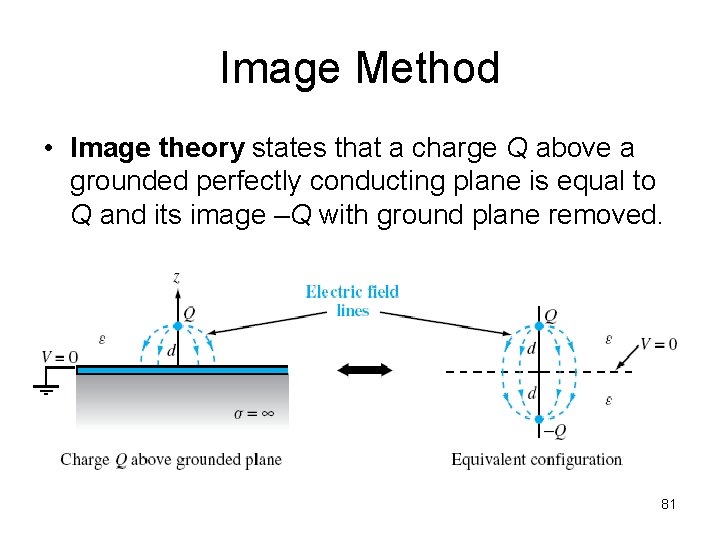
Image Method • Image theory states that a charge Q above a grounded perfectly conducting plane is equal to Q and its image –Q with ground plane removed. 81

Example 8 Use image theory to determine E at an arbitrary point P (x, y, z) in the region z > 0 due to a charge Q in free space at a distance d above a grounded conducting plane. 82

Solution to Example 8 • Charge Q is at (0, 0, d) and its image −Q is at (0, 0, −d) in Cartesian coordinates. Using Coulomb’s law, E at point P(x, y, z) due to two point charges: 83
 Universiti yang menawarkan bidang psikiatri di malaysia
Universiti yang menawarkan bidang psikiatri di malaysia Universiti putra malaysia
Universiti putra malaysia Curtis parry
Curtis parry Kalkulationsberechnung
Kalkulationsberechnung Cara pengiraan slt
Cara pengiraan slt Gred pensyarah universiti awam
Gred pensyarah universiti awam Akta 1976 itm
Akta 1976 itm Maksud tatarias
Maksud tatarias Malaysia malaysia malaysiansleereuters
Malaysia malaysia malaysiansleereuters Teknologi tenaga perlis consortium
Teknologi tenaga perlis consortium Iee regulations regarding 13a socket outlets
Iee regulations regarding 13a socket outlets Daerah perlis
Daerah perlis Ciri ciri tanah pamah
Ciri ciri tanah pamah Pengasasan negeri kedah
Pengasasan negeri kedah Perlis thompson principle
Perlis thompson principle Masa kemunduran kesultanan aceh darussalam
Masa kemunduran kesultanan aceh darussalam Teknologi tenaga perlis consortium sdn bhd
Teknologi tenaga perlis consortium sdn bhd Divergence in spherical coordinates example
Divergence in spherical coordinates example Energy density of electromagnetic waves
Energy density of electromagnetic waves Electromagnetic theory
Electromagnetic theory Electromagnetic theory
Electromagnetic theory Electromagnetic theory
Electromagnetic theory Electromagnetic theory
Electromagnetic theory Chapter 18 the electromagnetic spectrum and light
Chapter 18 the electromagnetic spectrum and light A health inspector is measuring the intensity of a sound
A health inspector is measuring the intensity of a sound Mechanical waves examples
Mechanical waves examples Longitudinal wave vs transverse wave
Longitudinal wave vs transverse wave Mechanical and electromagnetic waves
Mechanical and electromagnetic waves Electromagnetic energy def
Electromagnetic energy def Difference between electromagnetic waves and sound waves
Difference between electromagnetic waves and sound waves Energy density em wave
Energy density em wave Longest to shortest wavelength
Longest to shortest wavelength Edwin hubble
Edwin hubble Em waves song lyrics
Em waves song lyrics Conclusion of electromagnetic spectrum
Conclusion of electromagnetic spectrum Mechanical waves and electromagnetic waves similarities
Mechanical waves and electromagnetic waves similarities Electromagnetic particle inspection
Electromagnetic particle inspection Electromagnetic waves characteristics
Electromagnetic waves characteristics Electromagnetic waves frequency
Electromagnetic waves frequency Is light an electromagnetic wave
Is light an electromagnetic wave Mechanical vs electromagnetic waves
Mechanical vs electromagnetic waves Mechanical waves and electromagnetic waves similarities
Mechanical waves and electromagnetic waves similarities Electromagnetic spectrum foldable
Electromagnetic spectrum foldable Electromagnetic waves seeing objects and color
Electromagnetic waves seeing objects and color Electro magnetic chart
Electro magnetic chart Mnemonic for electromagnetic spectrum
Mnemonic for electromagnetic spectrum Wattmetric relay
Wattmetric relay Electromagnetic powerpoint template
Electromagnetic powerpoint template Electromagnetic spectrum micrometers
Electromagnetic spectrum micrometers Electromagnetic induction ppt
Electromagnetic induction ppt Lorentz force equation
Lorentz force equation Definition emc
Definition emc Fabrication of electromagnetic braking system
Fabrication of electromagnetic braking system Em spectrum mnemonic
Em spectrum mnemonic Electromagnetic spectrum foldable
Electromagnetic spectrum foldable Intensity of em wave
Intensity of em wave Electromagnetic oscillation pdf
Electromagnetic oscillation pdf James clerk maxwell theory of light
James clerk maxwell theory of light Electromagnetic speed log principle
Electromagnetic speed log principle Electromagnetic series
Electromagnetic series Is a seismic wave mechanical or electromagnetic
Is a seismic wave mechanical or electromagnetic Properties of waves
Properties of waves Two technicians are discussing electromagnetic induction
Two technicians are discussing electromagnetic induction Electromagnetic power formula
Electromagnetic power formula Principle of electromagnetic distance measurement
Principle of electromagnetic distance measurement Physics classroom
Physics classroom Light electromagnetic
Light electromagnetic Facts about electromagnetic radiation
Facts about electromagnetic radiation Section 1 what are electromagnetic waves
Section 1 what are electromagnetic waves Electromagnetic spectrum
Electromagnetic spectrum Electromagnetic oscillations and alternating current
Electromagnetic oscillations and alternating current Alternating current circuits and electromagnetic waves
Alternating current circuits and electromagnetic waves Electromagnetic wave power
Electromagnetic wave power Electromagnetic induction wind turbine
Electromagnetic induction wind turbine Light electromagnetic
Light electromagnetic Venn diagram of mechanical and electromagnetic waves
Venn diagram of mechanical and electromagnetic waves An ignition coil operates using the principle of
An ignition coil operates using the principle of Types of radiation in the electromagnetic spectrum
Types of radiation in the electromagnetic spectrum Momentum of electromagnetic field
Momentum of electromagnetic field Electromagnetic testing (et)
Electromagnetic testing (et) Conclusion of electromagnetic induction
Conclusion of electromagnetic induction Energy of em wave
Energy of em wave What is the electromagnetic spectrum
What is the electromagnetic spectrum Intensity of wave
Intensity of wave