EED 2008 Electromagnetic Theory zgr TAMER Vectors Divergence

EED 2008: Electromagnetic Theory Özgür TAMER Vectors Divergence and Stokes Theorem

Vector integration Linear integrals Vector area and surface integrals Volume integrals

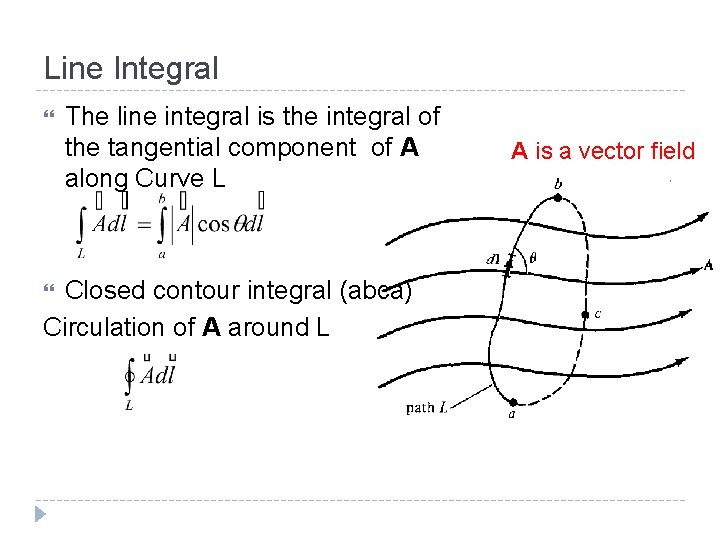
Line Integral The line integral is the integral of the tangential component of A along Curve L Closed contour integral (abca) Circulation of A around L A is a vector field

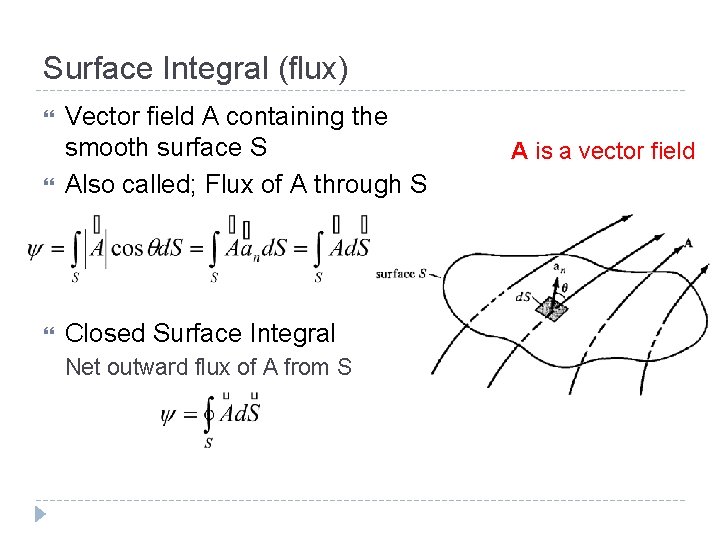
Surface Integral (flux) Vector field A containing the smooth surface S Also called; Flux of A through S Closed Surface Integral Net outward flux of A from S A is a vector field

Volume Integral of scalar over the volume V

Vector Differential Operator The vector differential operator (gradient operator), is not a vector in itself, but when it operates on a scalar function, for example, a vector ensues.

Gradient Physical meaning of T : A variable position vector r to describe an isothermal surface : T Since dr lies on the isothermal plane… dr and Thus, T must be perpendicular to dr. Since dr lies in any direction on the plane, T must be perpendicular to the tangent plane at r. T is a vector in the direction of the most rapid change of T, and its magnitude is equal to this rate of change. if A·B = 0 The vector A is zero The vector B is zero = 90°

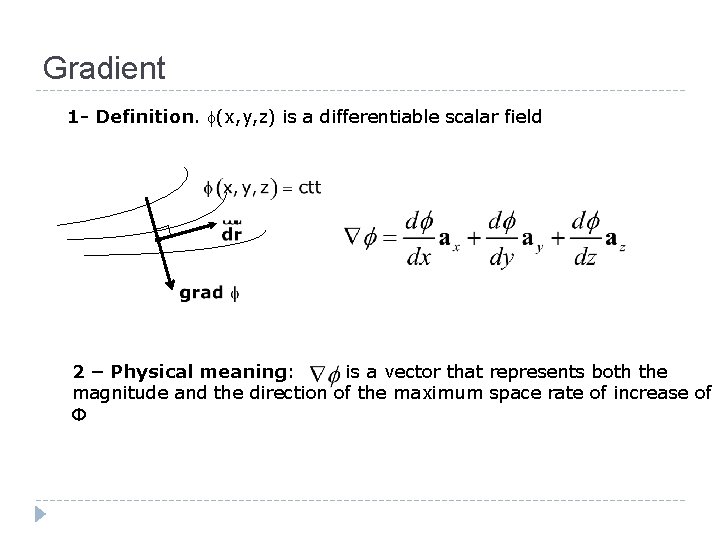
Gradient 1 - Definition. f(x, y, z) is a differentiable scalar field 2 – Physical meaning: is a vector that represents both the magnitude and the direction of the maximum space rate of increase of Φ

Divergence The operator is of vector form, a scalar product can be obtained as : A is the net flux of A per unit volume at the point considered, counting vectors into the volume as negative, and vectors out of the volume as positive. Output - input : the net rate of mass flow from unit volume

Divergence Ain Aout The flux leaving the one end must exceed the flux entering at the other end. The tubular element is “divergent” in the direction of flow. Therefore, the operator is frequently called the “divergence” : Divergence of a vector

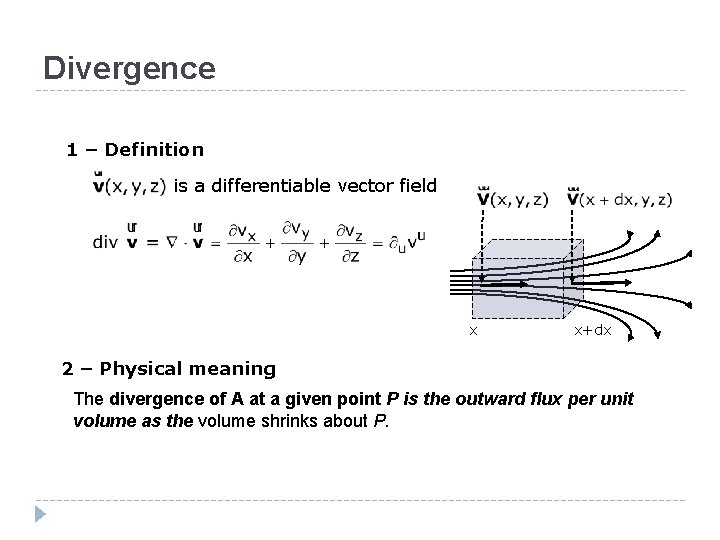
Divergence 1 – Definition is a differentiable vector field x x+dx 2 – Physical meaning The divergence of A at a given point P is the outward flux per unit volume as the volume shrinks about P.

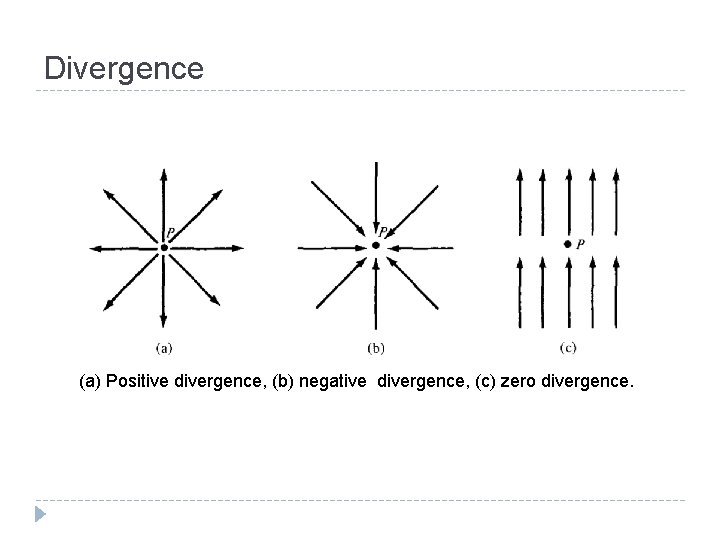
Divergence (a) Positive divergence, (b) negative divergence, (c) zero divergence.

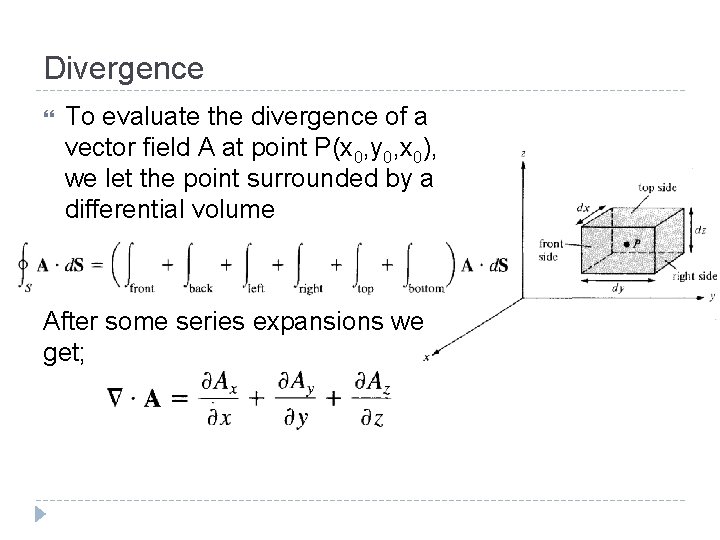
Divergence To evaluate the divergence of a vector field A at point P(x 0, y 0, x 0), we let the point surrounded by a differential volume After some series expansions we get;

Divergence Cylindrical Coordinate System Spherical Coordinate System

Divergence Properties of the divergence of a vector field It produces a scalar field The divergence of a scalar V, div V, makes no sense

Curl 1 – Definition. The curl of a is an axial (or rotational) vector whose magnitude is the maximum circulation of A per unit area as the area lends to zero and whose direction is the normal direction of the area when the area is oriented so as to make the circulation maximum.

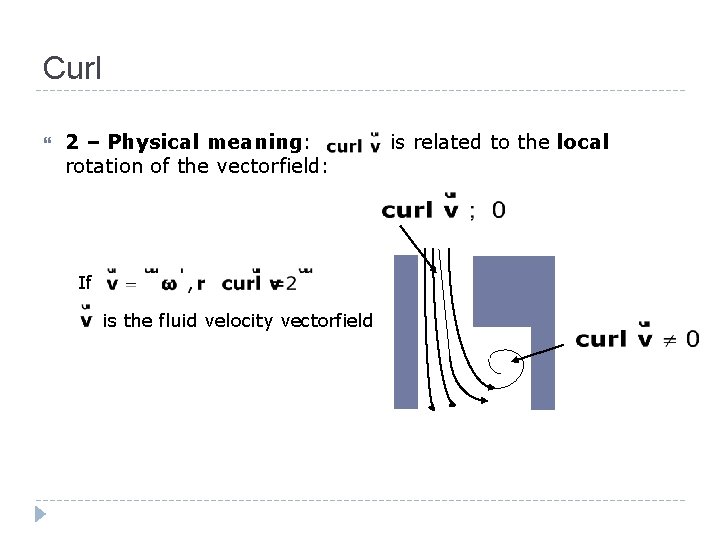
Curl 2 – Physical meaning: rotation of the vectorfield: If is the fluid velocity vectorfield is related to the local

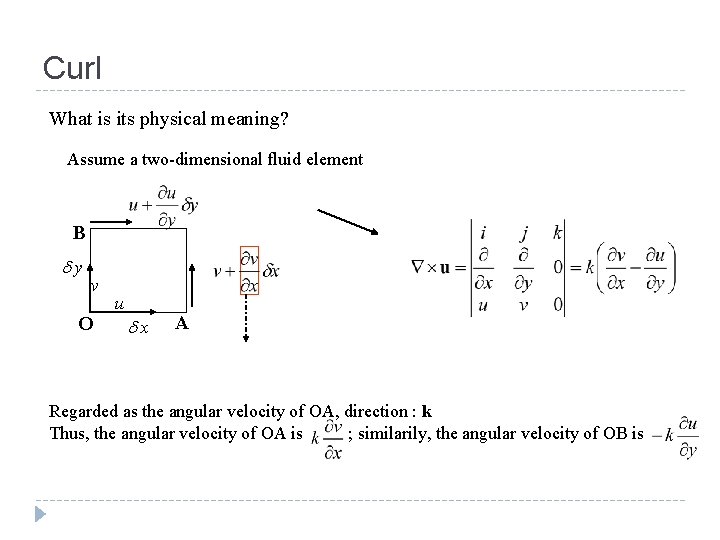
Curl What is its physical meaning? Assume a two-dimensional fluid element B y v O u x A Regarded as the angular velocity of OA, direction : k Thus, the angular velocity of OA is ; similarily, the angular velocity of OB is

Curl The angular velocity of the fluid element is the average of the two angular velocities : B y v O u x A This value is called the “vorticity” of the fluid element, which is twice the angular velocity of the fluid element. This is the reason why it is called the “curl” operator.

Curl Cartesian Coordinates

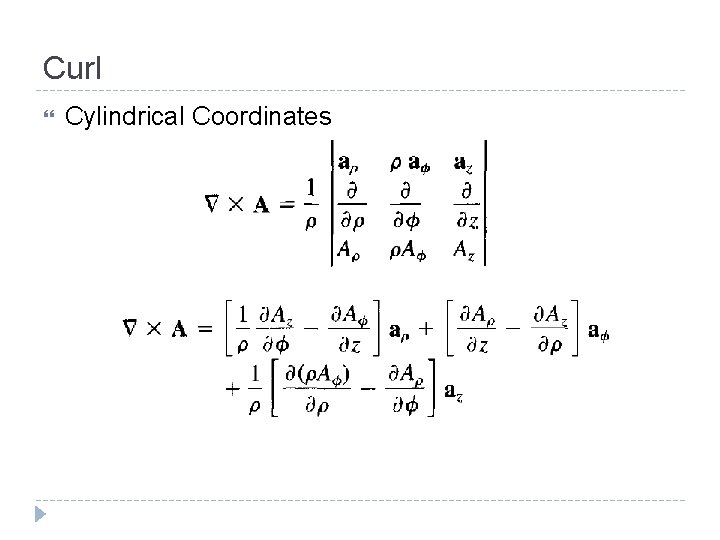
Curl Cylindrical Coordinates

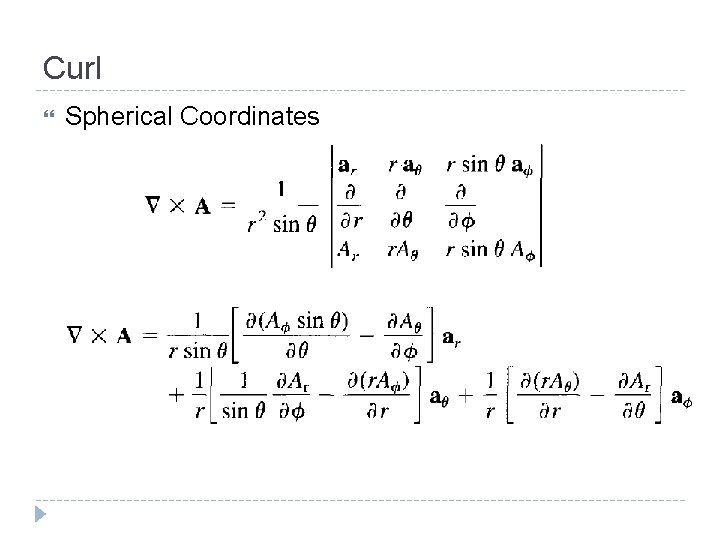
Curl Spherical Coordinates

Stokes’ Theorem If there is a vector field A, then the line integral of A taken round C is equal to the surface integral of × A taken over S : Two-dimensional system Considering a surface S having element d. S and curve C denotes the curve :

Stokes’ Theorem Stokes's theorem states that ihe circulation of a vector field A around a (closed) pth L is equal to the surface integral of the curl of A over the open surface S bounded by L provided that A and are continuous on S

Laplacian 1 – Scalar Laplacian. The Laplacian of a scalar field V, written as. is the divergence of the gradient of V. Divergence of a vector is scalar The Laplacian of a scalar field is scalar Gradient of a scalar is vector

Laplacian In cartesian coordinates In Cylindrical coordinates In Spherical Coordinates

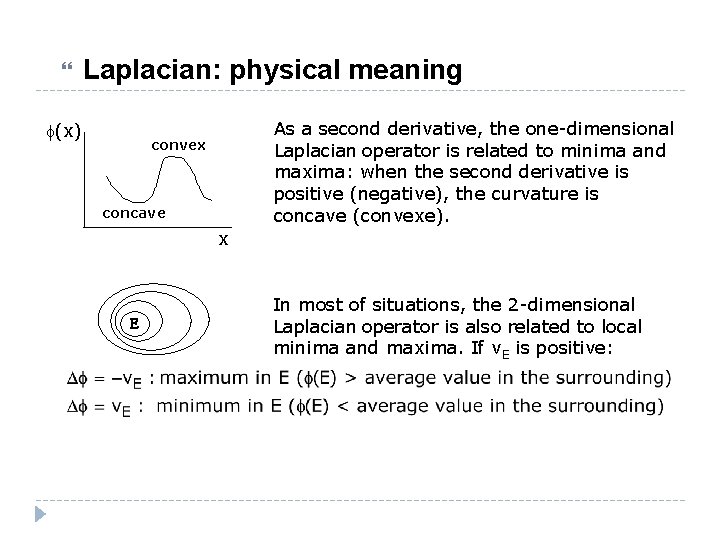
Laplacian: physical meaning f(x) As a second derivative, the one-dimensional Laplacian operator is related to minima and maxima: when the second derivative is positive (negative), the curvature is concave (convexe). convex concave x E In most of situations, the 2 -dimensional Laplacian operator is also related to local minima and maxima. If v. E is positive:

Laplacian A scalar field V is said to be harmonic in a given region if its Laplacian vanishes in that region.

Laplacian of a vector: is defined as the gradient of the divergence of A minus the curl of A; Only for the cartesian coordinate system;

3. Differential operators Summary Operator grad div curl Laplacian is a vector a scalar (resp. a vector) concerns a scalar field a vector field a scalar field (resp. a vector field) Definition resp.

Gauss’ Divergence Theorem The divergence theorem states that the total outward flux of a vector field A through the closed surface S is the same as the volume integral of the divergence of A The theorem applies to any volume v bounded by the closed surface S

Gauss’ Divergence Theorem Ain Aout The tubular element is “divergent” in the direction of flow. The net rate of mass flow from unit volume We also have : The surface integral of the velocity vector u gives the net volumetric flow across the surface The mass flow rate of a closed surface (volume)

Stokes’ Theorem Gauss’ Divergence Theorem

Classification of Vector Fields A vector field is characterized by its divergence and curl

Classification of Vector Fields Solenoidal Vector Field: A vector field A is said to be solenoidal (or divergenceless) if Such a field has neither source nor sink of flux, flux lines of A entering any closed surface must also leave it.

Classification of Vector Fields A vector field A is said to be irrotational (or potential) if In an irrotational field A, the circulation of A around a closed path is identically zero. This implies that the line integral of A is independent of the chosen path An irrotational field is also known as a conservative field

Stokes formula: vector field global circulation Theorem. If S(C) is any oriented surface delimited by C: S(C) C y . . P . Sketch of proof. Vy . Vx x … and then extend to any surface delimited by C.

Divergence Formula: global conservation laws Theorem. If V(C) is the volume delimited by S x x+dx Sketch of proof. Flow through the oriented elementary planes x = ctt and x+dx = ctt : -Vx(x, y, z). dydz + Vx (x+dx, y, z). dydz and then extend this expression to the lateral surface of the cube. Other expression: extended to the vol. of the elementary cube: