PUSAT PENGAJIAN DIPLOMA UNIVERSITI MALAYSIA PERLIS Uni MAP



























- Slides: 30

PUSAT PENGAJIAN DIPLOMA UNIVERSITI MALAYSIA PERLIS (Uni. MAP) DNT 245 SENSORS & MEASUREMENTS Chapter 2 Statistical Analysis Lecturer : Nor Shaifudin Bin Abdul Hamid

Introduction 2 Measurement processes usually introduce a certain amount of variability or randomness. Randomness can be caused by uncontrolled variables affecting the measurand or lack of precision in the measuring process. Random errors that are the most amenable to the methods of statistical analysis. (dipersetujui)

Introduction 3 Statistical tools are needed : - To determine the characteristics of experimental data - To estimate the uncertainty of experimental data - To plan experiments when there is a large no. of variables

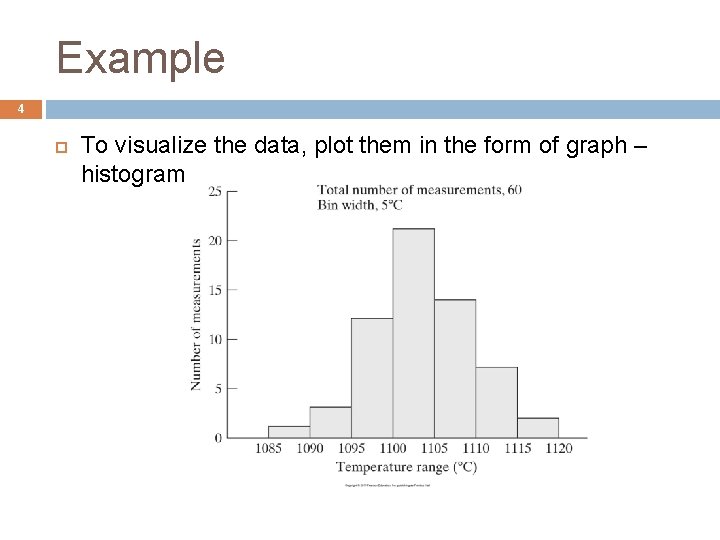
Example 4 To visualize the data, plot them in the form of graph – histogram

Example 5 To create the graph, arrange the data into groups called bins Each bins has the same width (range of Temperature)

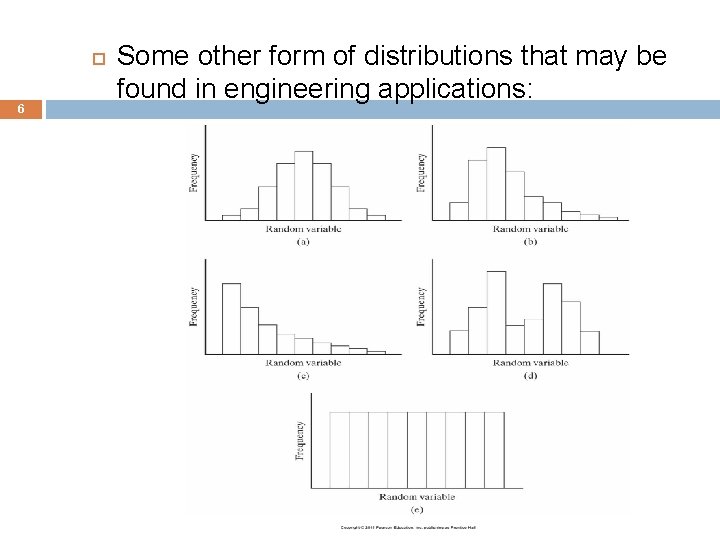
6 Some other form of distributions that may be found in engineering applications:

General Concepts & Definitions 7 Population – comprises the entire set of objects , measurements and observation on whose properties are under consideration and about which some generalization are to be made. - Ex: the entire set of 60 W electric bulbs that have been produced in a production batch. Sample – a representative subset of a population on which an experiment is performed & numerical data are obtained. - Ex: 10 light bulbs are selected from a production batch of 10, 000.

General Concepts & Definitions 8 Sample space – the set of all possible outcomes of an experiment. Ex: 6 possible outcomes in casting a fair dice (discrete sample space), temperature measurement coming out from furnace (continuous sample space) dice http: //www. schoolatoz. nsw. edu. au/homework-andstudy/maths-a-to-z/

General Concepts & Definitions 9 Random variable – numerically valued function defined for the population , for every outcome of an experiment. -can be continuous or discrete. Examples ØA coin is tossed ten times. The random variable X is the number of tails that are noted. X can only take the values 0, 1, . . . , 10, so X is a discrete random variable. ØA light bulb is burned until it burns out. The random variable Y is its lifetime in hours. Y can take any positive real value, so Y is a continuous random variable.

General Concepts & Definitions 10 Distribution function – a graphical /mathematical relationship that is used to represent the values of the random variables. Event – the outcome of random experiment Probability – the chance of occurrence of an event in an experiment. - dividing the number of successful occurrences by the total number of trials. - ex : 50% chance that the outcome of tossing a coin will be heads.

Measures of Central Tendency 11 Mean (average) For sample: Where x’s – the value of the sample, n – the number of measurements. For population : Where N – finite number of elements

Info… 12

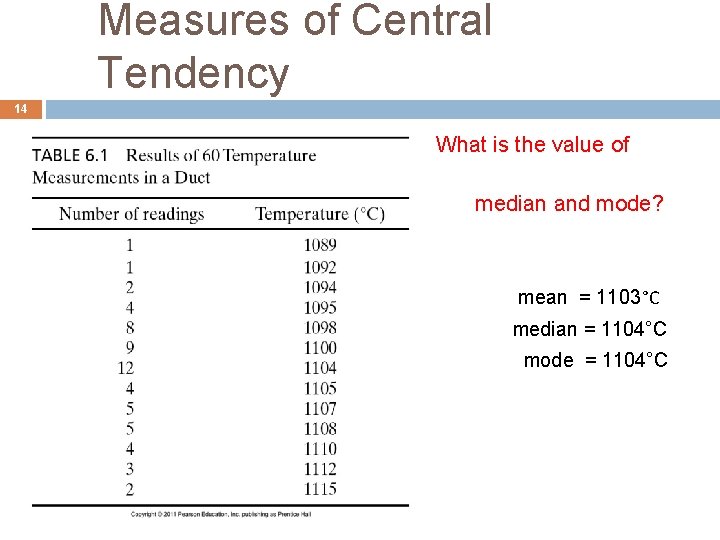
Measures of Central Tendency 13 Median – the value at the center of the set if the measurands are arranged in descending or ascending order. Mode – the peak value of the probability of occurrence of the event.

Measures of Central Tendency 14 What is the value of mean, median and mode? mean = 1103°C median = 1104°C mode = 1104°C §

Measures of Dispersion 15 • Dispersion (penyerakan) – the spread or variability of the data. -The more spread apart the data, the higher the deviation. a) Deviation (sisihan) : b) Mean deviation:

Measures of Dispersion 16 Standard Deviation are measures of how spread out a distribution is, or it mean measures of variability. c) Population standard deviation : ** µ mean N population size xi individual x values d) Sample standard deviation : ** n sample size Sample standard deviation is used when the data of a sample are used to estimate the population standard

Measures of Dispersion 17 The variance is the average of the squared differences from the Mean. variance = σ2 for population S 2 for sample Used as a measure of how far a set of numbers are spread out from each other

Example 18 Variance 196. 84 121. 66 163. 08 257. 92 i. ii. iii. Mean = 1103 Variance = 1976/60 i. = 33. 490 C 2 Standard deviation = 5. 790 C 202. 41 82. 63 11. 29 15. 52 78. 8 123. 5 194. 32 241. 38 286. 56

Probability 19 Probability is a numerical value expressing the likelihood (kemungkinan) of occurrence of an event relative to all possibilities in a sample space. Example: in the case of tossing a fair dice, the probability of having a no 3 is 1/6. Solution: Total no. of possible outcome = number {1, 2, 3, 4, 5, 6} = 6 No. of occurance of event A = number {3} = 1 P(A) = 1/6 For a continuous random variable x, the probability is P(x) For discrete random variable xi, the probability is P(xi)

Standard properties associated with probability: 20 1. Probability is always a positive number with a maximum of 1: 2. If an event A is certain to occur; 3. If an event A is certain not to occur; 4. If event Ā is the complement of event A (this means that if event A occurs, event Ā cannot occur);

21 Standard properties associated with probability: 5. If the events A and B are mutually exclusive (i. e. , the probability of simultaneous occurrence of A and B is zero), then the probability of occurrence of event A or event B; Example 001: in the case of tossing a fair dice, the probability of having a 3 or 6 is

22 Standard properties associated with probability: 6. If the events A and B are independent of each other (this means that their occurrences do not depend on each other), the probability that both A and B will occur together is:

23 Standard properties associated with probability: Example 002: consider an assembly of two pieces, A and B, in a machine, such as a computer and monitor. A and B are manufactured by two different companies. We are told that there is a 5% chance that A is defective and a 2% chance that B is defective. The probability that both A and B are defective is then;

24 Standard properties associated with probability: 7. The probability of occurrence A or B or both, represented by P(AUB) (read “the probability of A union B”);

25 Standard properties associated with probability: Example 003: from Example 002 the probability of having A or B or both be defective will be;

26 Probability Distribution Functions An important function of statistics which use information from a sample to predict the behavior of a population. It is modeled or represented Mathematically and/or Graphically to show the relationship of the random variables using sample data. For Discrete RV : Probability Mass Function (PMS) For Continuous RV : Probability Density function (PDF)

Probability Mass Functions 27 The sum of the probabilities of all possible values of x must be 1: The mean of the population for a discrete random variable is given by The quantity μ is also called the expected value of x , E(x). The variance of the population is given by

Probability Density Function 28 To evaluate the probability that x will occur in a finite interval from x=a to x=b , the equation can be integrated to obtain If the limits of integration are extended to –ve and +ve infinity, the probability will be:

Condition if 29 Then X is a random discrete variable with: i. iii. iv. for all xi known as probability function of X

Probability Density Function 30 The mean of population with PDF is: - Also called the expected value of random variable , E(x) The variance of population is:
 Perkhidmatan psikiatri di malaysia
Perkhidmatan psikiatri di malaysia Universiti putra malaysia
Universiti putra malaysia Diploma sejarah dan tamadun islam
Diploma sejarah dan tamadun islam Diploma pengajian al quran dan sunnah separuh masa
Diploma pengajian al quran dan sunnah separuh masa Pusat pengajian perumahan bangunan dan perancangan
Pusat pengajian perumahan bangunan dan perancangan Pusat pengajian pendidikan uum
Pusat pengajian pendidikan uum Maksud slt
Maksud slt Skim perkhidmatan pensyarah universiti
Skim perkhidmatan pensyarah universiti Akta 173 uitm
Akta 173 uitm Sepotong bina ayat
Sepotong bina ayat Sitasis
Sitasis Sitasi jurnal
Sitasi jurnal Malaysia malaysia malaysiansleereuters
Malaysia malaysia malaysiansleereuters Teknologi tenaga perlis consortium
Teknologi tenaga perlis consortium Ckt motor perlis
Ckt motor perlis Dewan jps perlis
Dewan jps perlis Dataran selangor dan hilir perak
Dataran selangor dan hilir perak Gelaran pemerintah kedah dan kelantan
Gelaran pemerintah kedah dan kelantan Perlis thompson principle
Perlis thompson principle Masa kemunduran kesultanan aceh darussalam
Masa kemunduran kesultanan aceh darussalam Scr forced commutation
Scr forced commutation Editable malaysia map
Editable malaysia map Kod geografi stpm
Kod geografi stpm Sijil pengajian al quran
Sijil pengajian al quran Pendekatan moden/kontemporari
Pendekatan moden/kontemporari Pelan strategik kpt
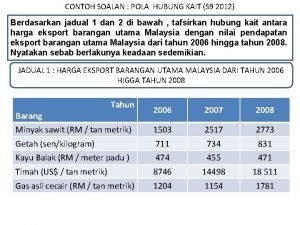
Pelan strategik kpt Pola hubung kait
Pola hubung kait Carta pengajian am
Carta pengajian am Pola banding pengajian am
Pola banding pengajian am Elearning utmspace
Elearning utmspace Fakulti pengajian pendidikan upm
Fakulti pengajian pendidikan upm