UNIVERSITI MALAYSIA PERLIS EKT 2414 ELECTROMAGNETIC THEORY CHAPTER


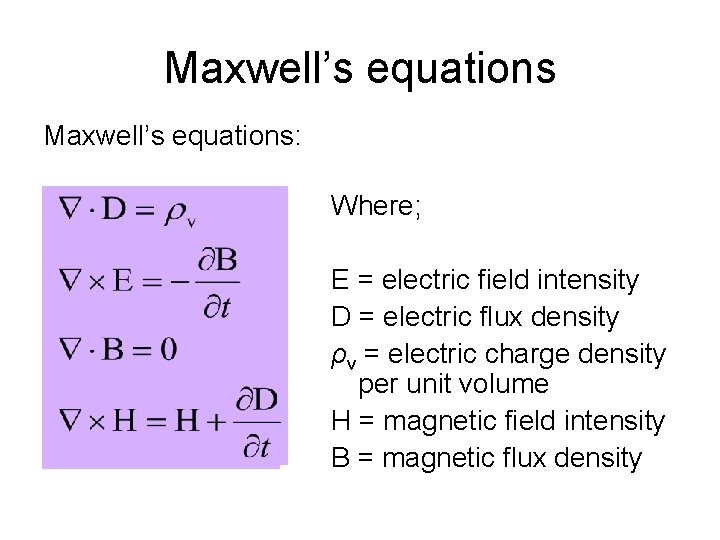



































- Slides: 63

UNIVERSITI MALAYSIA PERLIS EKT 241/4: ELECTROMAGNETIC THEORY CHAPTER 4 – MAGNETOSTATICS

Chapter Outline • • • Maxwell’s Equations Magnetic Forces and Torques The total electromagnetic force, known as Lorentz force Biot- Savart’s law Gauss’s law for magnetism Ampere’s law for magnetism Magnetic Field and Flux Vector magnetic potential Properties of 3 different types of material Boundary conditions between two different media Self inductance and mutual inductance Magnetic energy
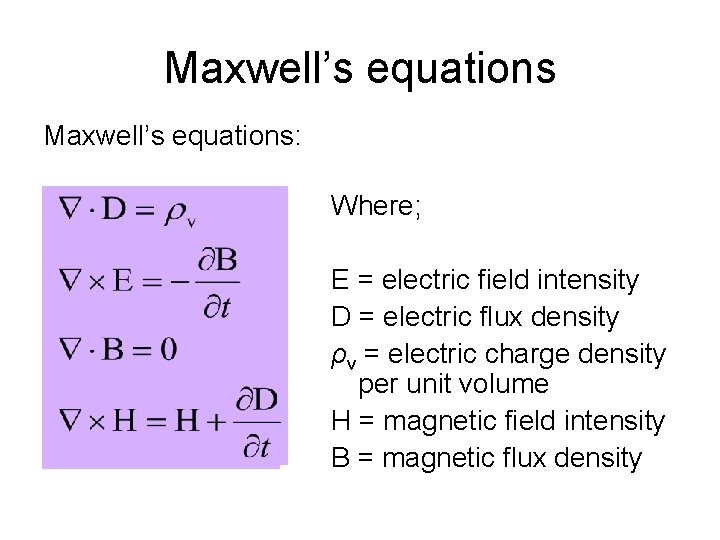
Maxwell’s equations: Where; E = electric field intensity D = electric flux density ρv = electric charge density per unit volume H = magnetic field intensity B = magnetic flux density

Maxwell’s equations • For static case, ∂/∂t = 0. • Maxwell’s equations is reduced to: Electrostatics Magnetostatics

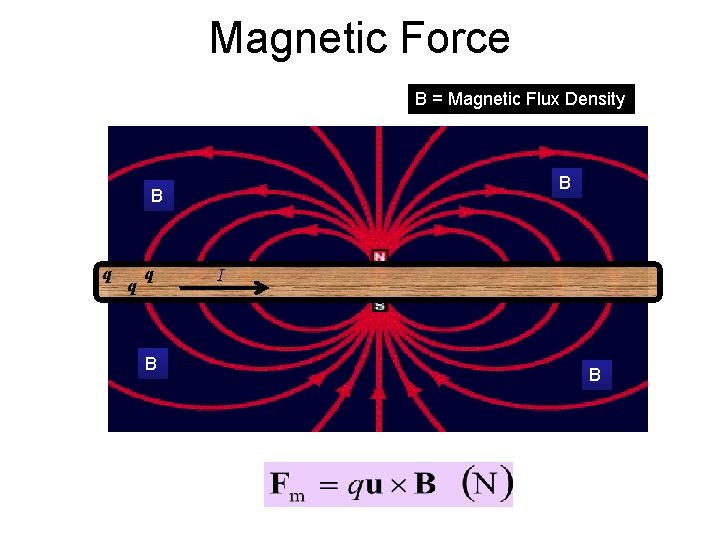
Magnetic Force B = Magnetic Flux Density B B q q q B I B

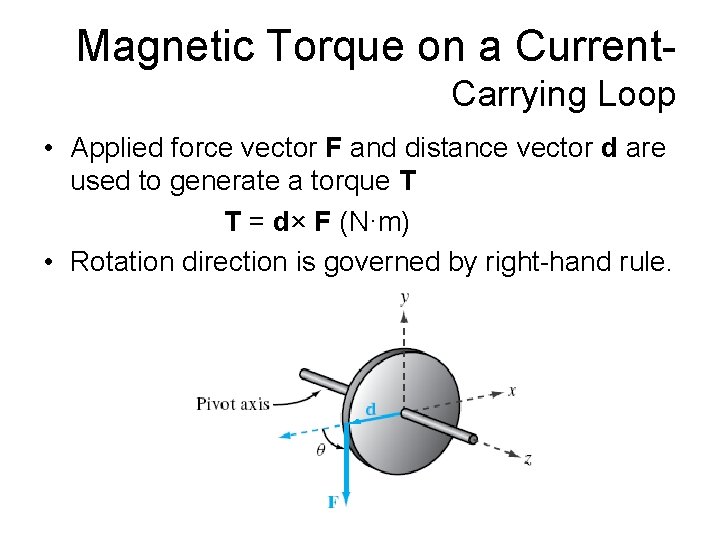
Magnetic Torque on a Current. Carrying Loop • Applied force vector F and distance vector d are used to generate a torque T T = d× F (N·m) • Rotation direction is governed by right-hand rule.

Magnetic Forces and Torques • The electric force Fe per unit charge acting on a test charge placed at a point in space with electric field E. • When a charged particle moving with a velocity u passing through that point in space, the magnetic force Fm is exerted on that charged particle. where B = magnetic flux density (Cm/s or Tesla T)

Magnetic Forces and Torques • If a charged particle is in the presence of both an electric field E and magnetic field B, the total electromagnetic force acting on it is:

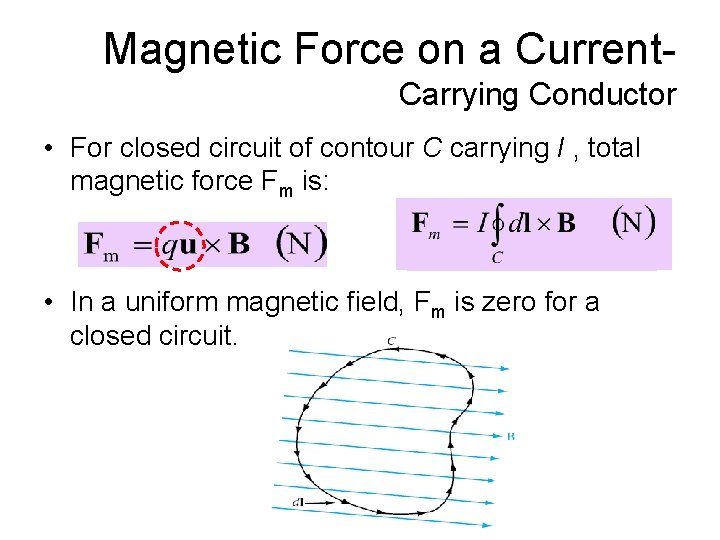
Magnetic Force on a Current. Carrying Conductor • For closed circuit of contour C carrying I , total magnetic force Fm is: • In a uniform magnetic field, Fm is zero for a closed circuit.

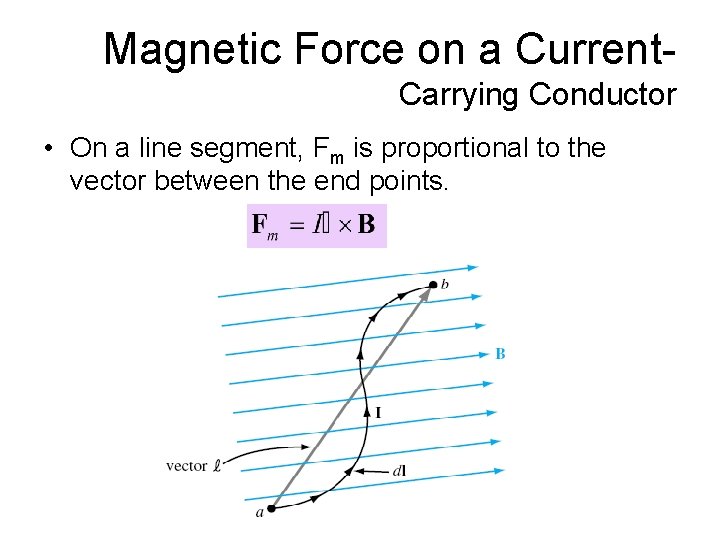
Magnetic Force on a Current. Carrying Conductor • On a line segment, Fm is proportional to the vector between the end points.

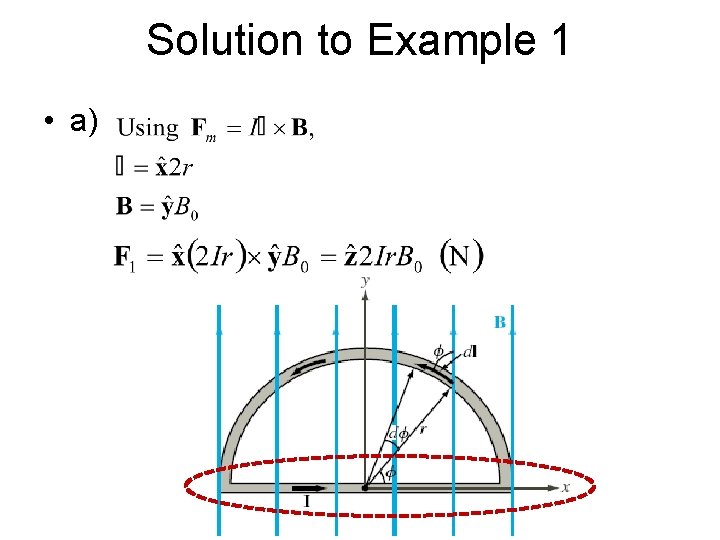
Example 1 The semicircular conductor shown carries a current I. The closed circuit is exposed to a uniform magnetic field. Determine (a) the magnetic force F 1 on the straight section of the wire and (b) the force F 2 on the curved section.

Solution to Example 1 • a)


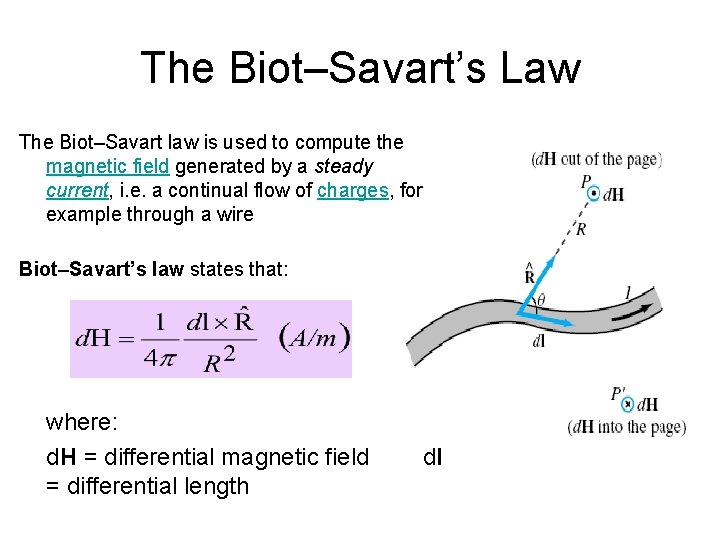
The Biot–Savart’s Law The Biot–Savart law is used to compute the magnetic field generated by a steady current, i. e. a continual flow of charges, for example through a wire Biot–Savart’s law states that: where: d. H = differential magnetic field = differential length dl

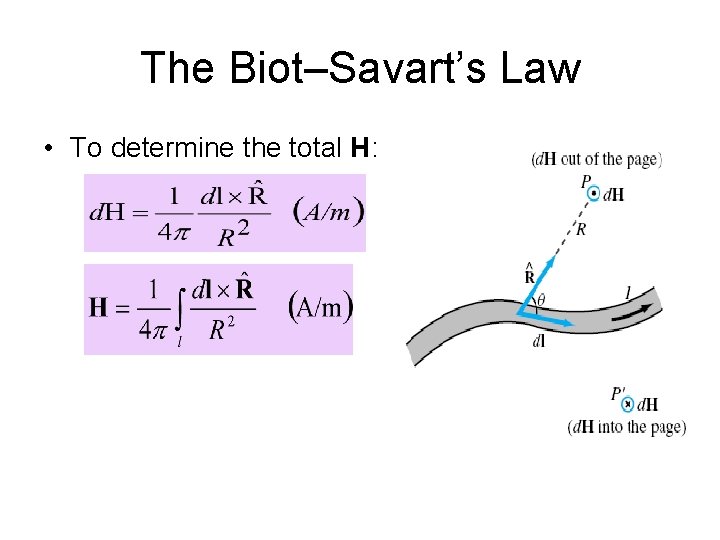
The Biot–Savart’s Law • To determine the total H:

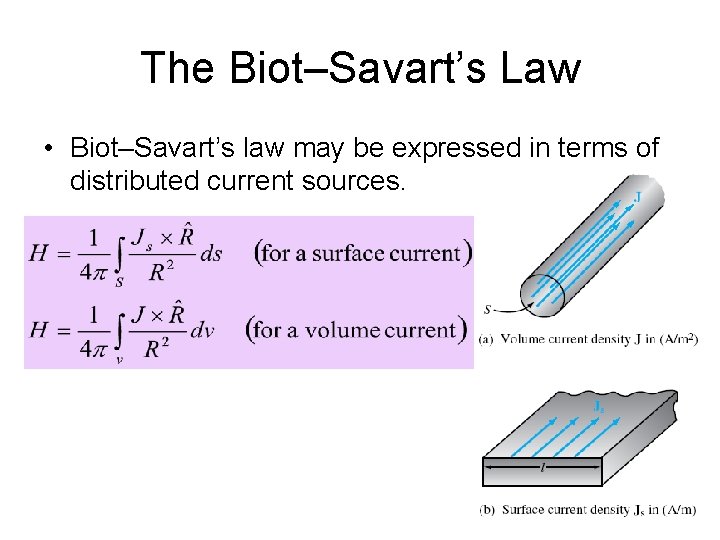
The Biot–Savart’s Law • Biot–Savart’s law may be expressed in terms of distributed current sources.

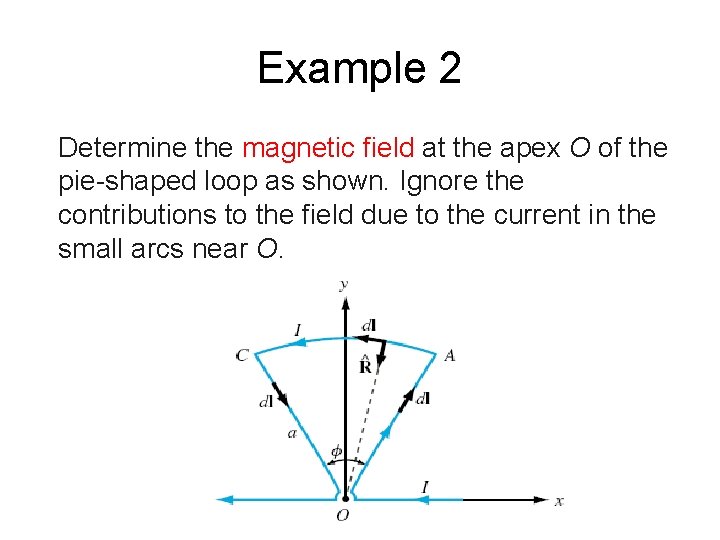
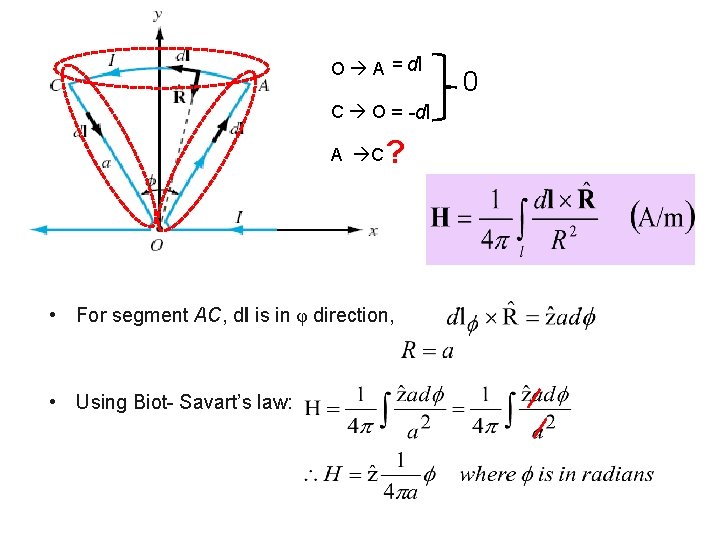
Example 2 Determine the magnetic field at the apex O of the pie-shaped loop as shown. Ignore the contributions to the field due to the current in the small arcs near O.

O A = dl C O = -dl A C ? • For segment AC, dl is in φ direction, • Using Biot- Savart’s law: 0

Gauss’s Law for Magnetism • Gauss’s law for magnetism states that: • Magnetic field lines always form continuous closed loops.


Ampere’s law for magnetism • Ampere’s law states that: • true for an infinite length of conductor H dl true for an infinite length of conductor C, +aø I, +az r

Magnetic Field of an infinite length of conductor From terms of Hφ: then re-arrange the equation in Hence, the magnetic field vector, H:

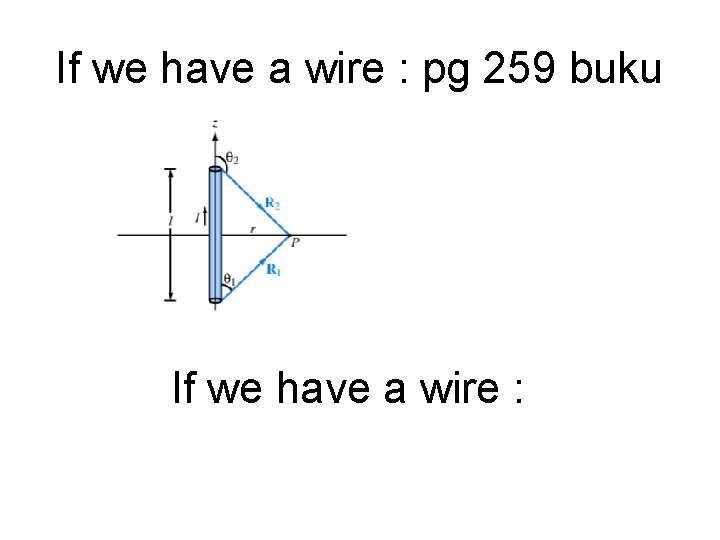
If we have a wire : pg 259 buku If we have a wire :

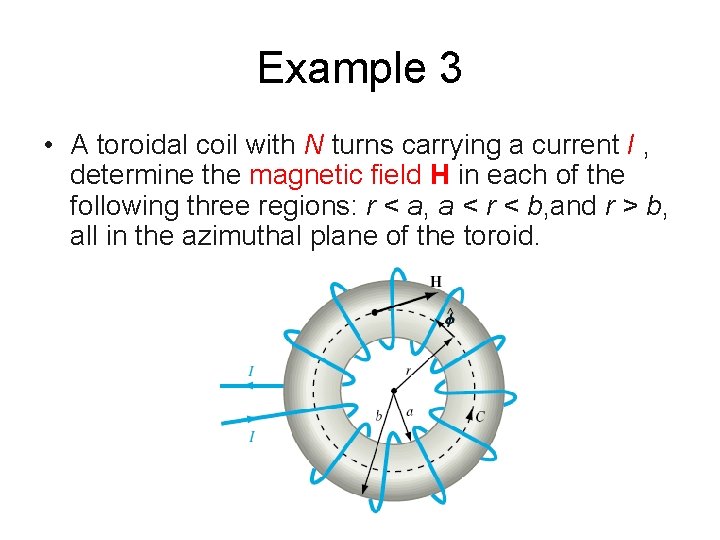
Example 3 • A toroidal coil with N turns carrying a current I , determine the magnetic field H in each of the following three regions: r < a, a < r < b, and r > b, all in the azimuthal plane of the toroid.

Solution to Example 3 • H = 0 for r < a as no current is flowing through the surface of the contour • H = 0 for r > b, as equal number of current coils cross the surface in both directions. • For a < r < b, we apply Ampere’s law: • Hence, H = NI/(2πr).

Magnetic Flux • The amount of magnetic flux, φ in Webers from magnetic field passing through a surface is found in a manner analogous to finding electric flux:

Example 4 An infinite length coaxial cable with inner conductor radius of 0. 01 m and outer conductor radius of 0. 05 m carrying a current of 2. 5 A exists along the z axis in the + az direction. Find the flux passing through the region between two conductors with height of 2 m in free space.

Solution to Example 4 Iaz=2. 5 A z 1) inner conductor radius = r 1 0. 01 m 2) outer conductor radius = r 2 0. 05 m 3) current of 2. 5 A (in the +az direction) 4) Flux radius = 2 m aø Flux, z xy r 2 r 1

Solution to Example 4 where d. S is in the aø direction. So, Therefore,

Vector Magnetic Potential • For any vector of vector magnetic potential A: • We are able to derive: . • Vector Poisson’s equation is given as: where

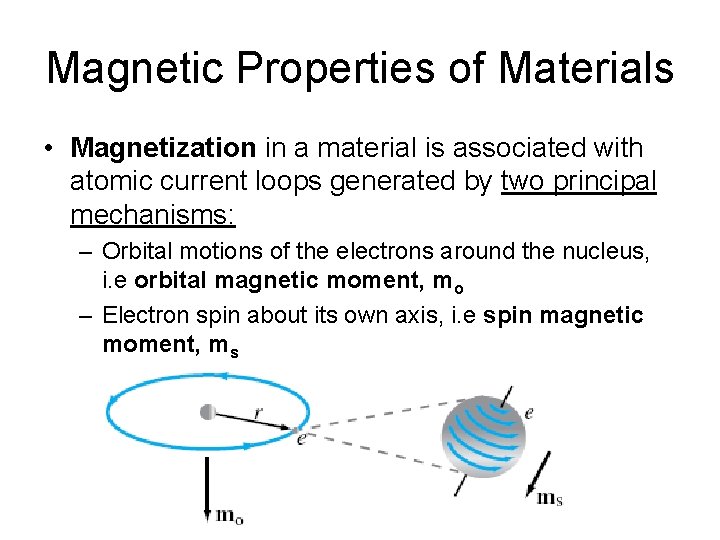
Magnetic Properties of Materials Diamagnetic Paramagnetic Ferromagnetic The behavior of magnetic dipole moments & magnetic susceptibility, of its atoms with an external magnetic field is used as a basis for classifying magnetic materials.

Magnetic Properties of Materials • Magnetization in a material is associated with atomic current loops generated by two principal mechanisms: – Orbital motions of the electrons around the nucleus, i. e orbital magnetic moment, mo – Electron spin about its own axis, i. e spin magnetic moment, ms

Magnetic Permeability • Magnetization vector M is defined as where = magnetic susceptibility (dimensionless) • Magnetic permeability is defined as: and to define the magnetic properties in term of relative permeability is defined as:

Magnetic Materials – Diamagnetic q metals have a very weak and negative susceptibility ( ) to magnetic field q slightly repelled by a magnetic field and the material does not retain the magnetic properties when the external field is removed q Most elements in the periodic table, including copper, silver, and gold, are diamagnetic.

Magnetic Materials Paramagnetic Ø Paramagnetic materials have a small and positive susceptibilities to magnetic fields. Ø slightly attracted by a magnetic field and the material does not retain the magnetic properties when the external field is removed. Ø Paramagnetic materials include magnesium, molybdenum, lithium, and tantalum.

Magnetic Materials – Diamagnetic, Paramagnetic • However, the absolute susceptibilities value of both materials is in the order 10 -5. Thus, can be ignored. Hence, we have Magnetic permeability: • Diamagnetic and paramagnetic materials include dielectric materials and most metals.

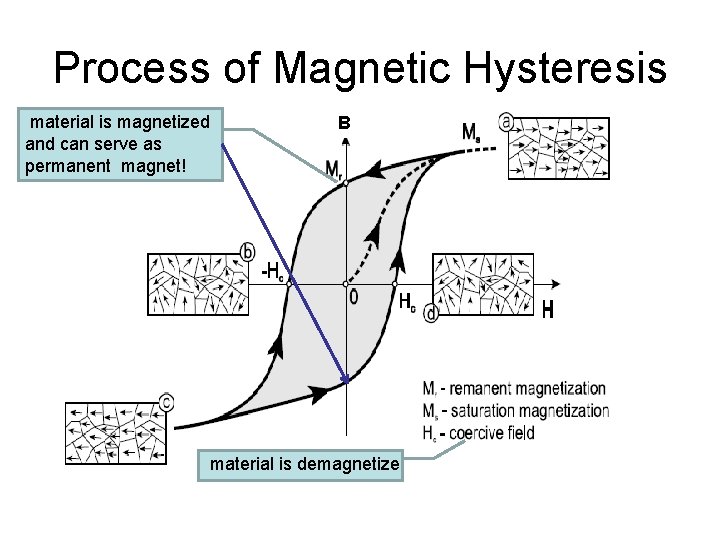
Magnetic Materials – Ferromagnetic Materials • Ferromagnetic materials is characterized by magnetized domain - a microscopic region within which the magnetic moments of all its atoms are aligned parallel to each other. • Hysteresis – “to lag behind”. It determines how easy/hard for a magnetic material to be magnetized and demagnetized.

Process of Magnetic Hysteresis material is magnetized and can serve as permanent magnet! B material is demagnetize

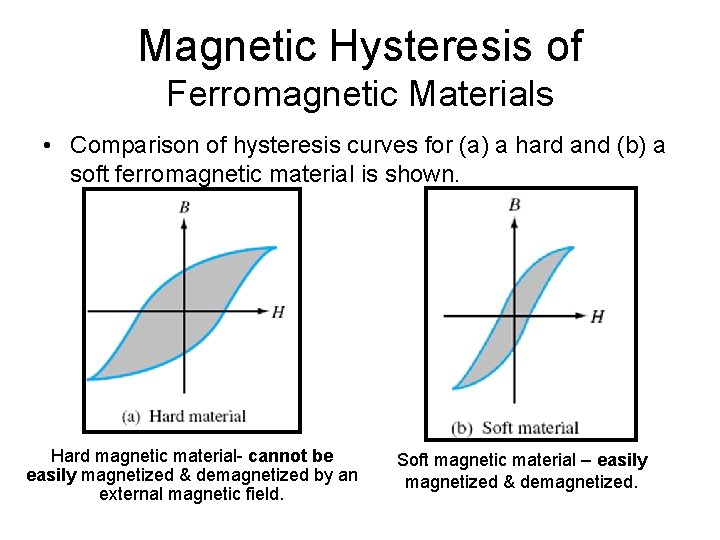
Magnetic Hysteresis of Ferromagnetic Materials • Comparison of hysteresis curves for (a) a hard and (b) a soft ferromagnetic material is shown. Hard magnetic material- cannot be easily magnetized & demagnetized by an external magnetic field. Soft magnetic material – easily magnetized & demagnetized.

Magnetic Hysteresis of Ferromagnetic Materials • Properties of magnetic materials as follows:

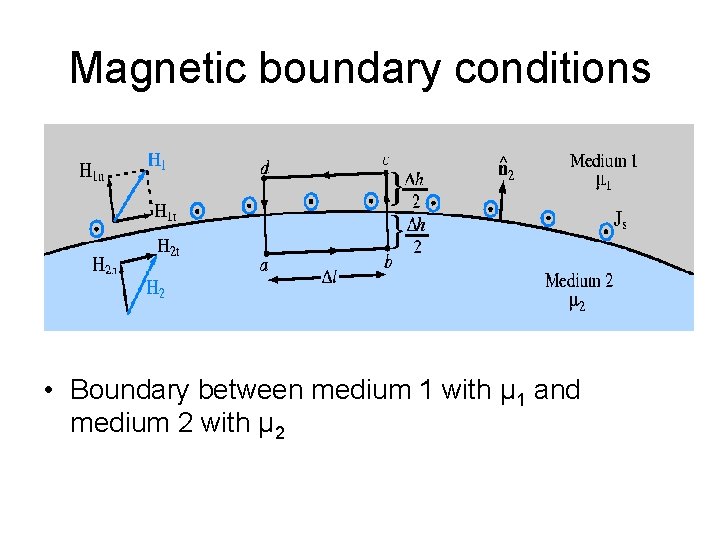
Magnetic boundary conditions • Boundary between medium 1 with μ 1 and medium 2 with μ 2

Magnetic boundary conditions • Boundary condition related to normal components of the electric field; • By analogy, application of Gauss’s law for magnetism, we get first boundary condition: • Since , • For linear, isotropic media, the first boundary condition which is related to H;

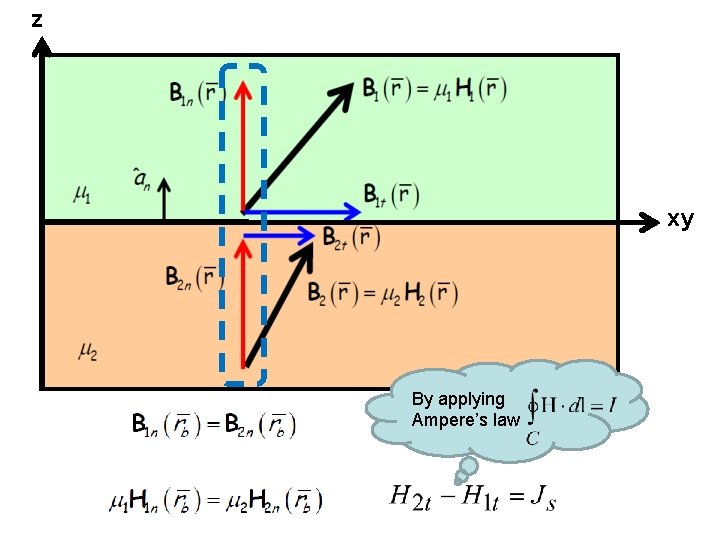
z xy By applying Ampere’s law

STOPMagnetic boundary conditions • The result is generalized to a vector form: • Where • However, surface currents can exist only on the surfaces of perfect conductors and perfect superconductors (infinite conductivities). • Hence, at the interface between media with finite conductivities, Js=0. Thus:

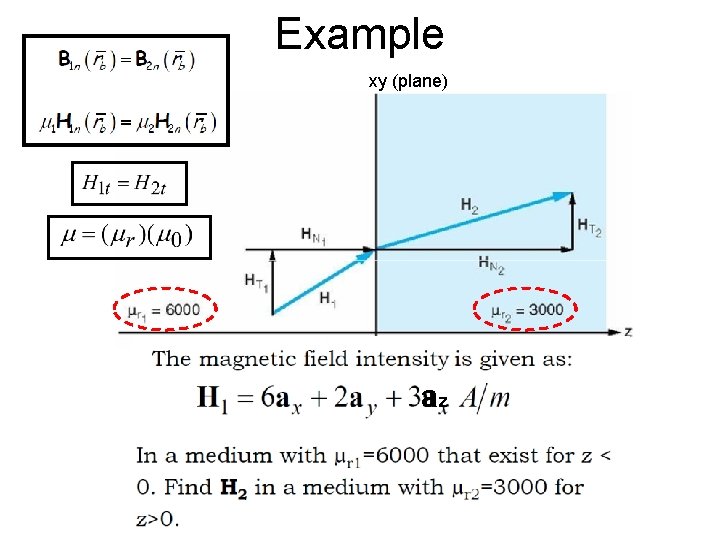
Example xy (plane) az

• Solution: 1) H 1 t = H 2 t thus, H 2 t = 6 ax + 2 ay 2) Hn 1 = 3 az, but, Hn 2 = ? ? μr 1 = 6000 ; μr 2 = 3000 ; 6000μ 0(3 az) = 3000 μ 0(Hn 2) Hn 2 = 6 az thus, H 2 =6 ax + 2 ay + 6 az

Inductance • An inductor is the magnetic analogue of an electrical capacitor. • Capacitor can store electric energy in the electric field present in the medium between its conducting surfaces. • Inductor can store magnetic energy in the volume comprising the inductors.

Solenoid calculate magnetic field in solenoid Self inductance: is the ratio of the magnetic flux linkage, Λ to the current I flowing through the structure. INDUCTANCE store magnetic energy Calculate Magnetic Energy Mutual inductance: produced by magnetic coupling between two different conducting structures.

Inductance • Example of an inductor is a solenoid - a coil consisting of multiple turns of wire wound in a helical geometry around a cylindrical core.

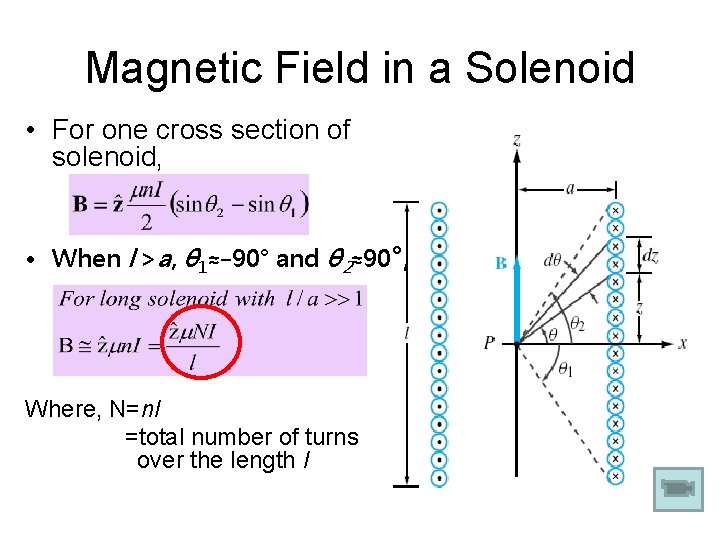
Magnetic Field in a Solenoid • For one cross section of solenoid, • When l >a, θ 1≈− 90° and θ 2≈90°, Where, N=nl =total number of turns over the length l

Self Inductance The self-inductance of a circuit is used to describe the reaction of the circuit to a changing current in the circuit, (The ratio of the magnetic flux to the current)

Self Inductance • Self-inductance of any conducting structure is the ratio of the magnetic flux linkage, Λ to the current I flowing through the structure. • Magnetic flux linkage, Λ is the total magnetic flux linking a given conducting structure.

Self Inductance • Magnetic flux, linking a surface S is given by: • In a solenoid with uniform magnetic field, the flux linking a single loop is:

Self Inductance – magnetic flux in solenoid

Self Inductance • Magnetic flux, linking a surface S is given by: • In a solenoid with uniform magnetic field, the flux linking a single loop is:

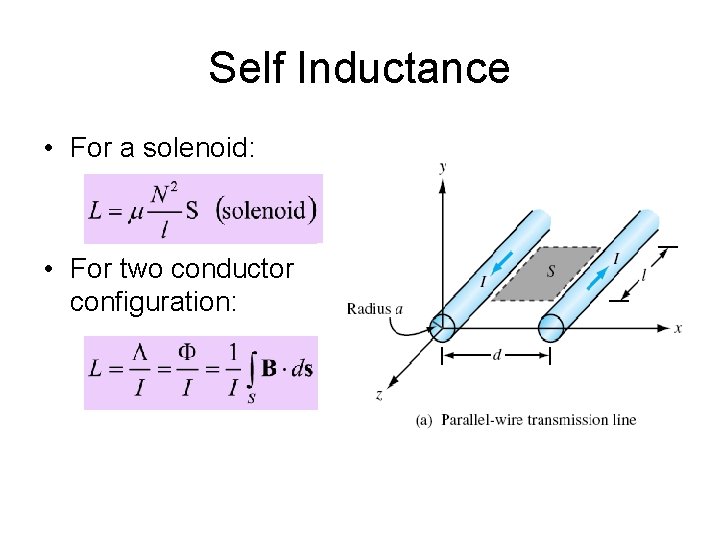
Self Inductance • For a solenoid: • For two conductor configuration:

Self Inductance for a solenoid Thus,

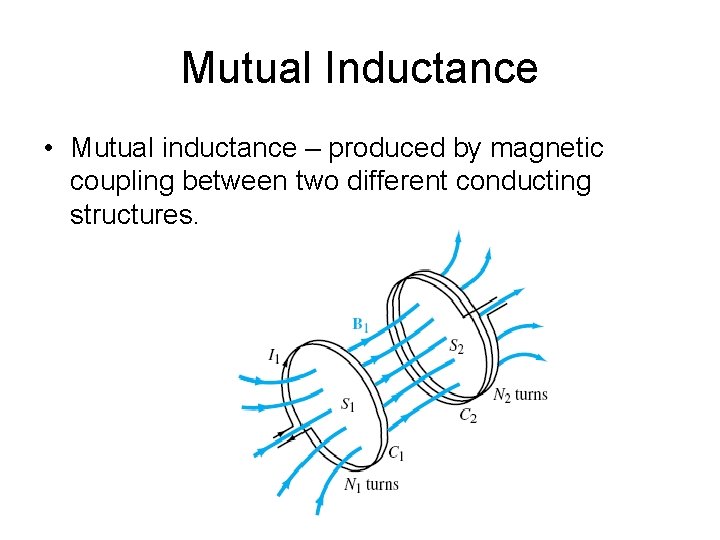
Mutual Inductance • Mutual inductance – produced by magnetic coupling between two different conducting structures.

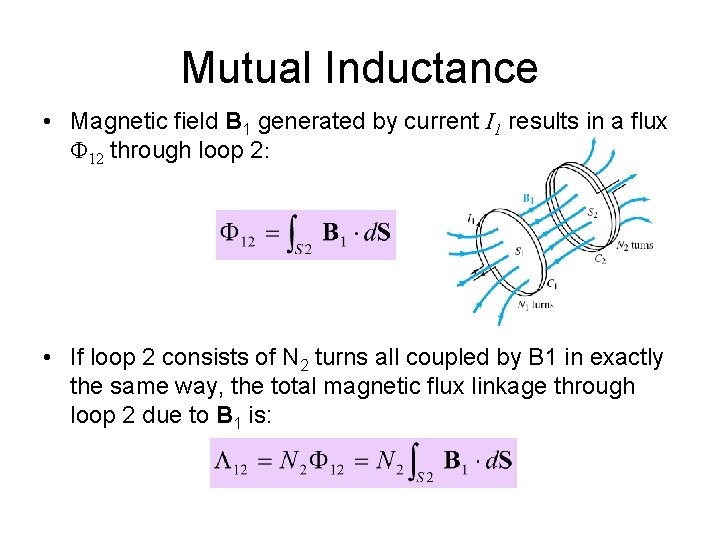
Mutual Inductance • Magnetic field B 1 generated by current I 1 results in a flux Φ 12 through loop 2: • If loop 2 consists of N 2 turns all coupled by B 1 in exactly the same way, the total magnetic flux linkage through loop 2 due to B 1 is:

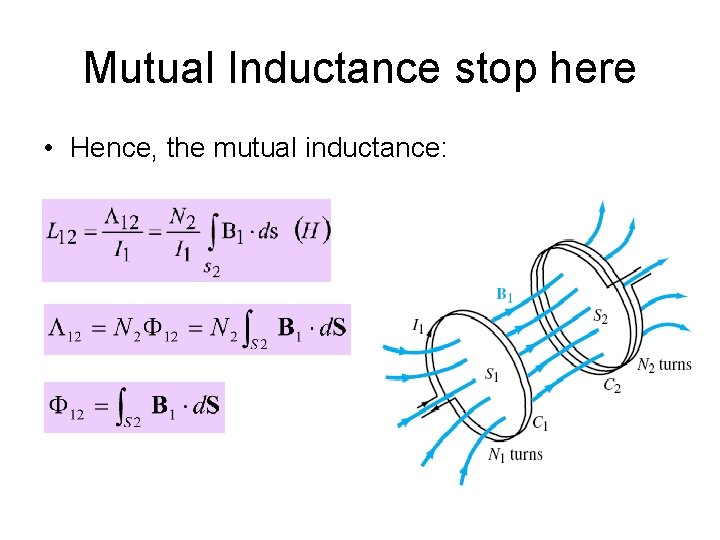
Mutual Inductance stop here • Hence, the mutual inductance:

Magnetic Energy tahun 4 • Consider an inductor with an inductance L connected to a current source. • The current I flowing through the inductor is increased from zero to a final value I. • The energy expended in building up the current in the inductor: • i. e the magnetic energy stored in the inductor

Magnetic Energy • Magnetic energy density (for solenoid): • i. e magnetic energy per unit volume • Magnetic energy in magnetic field:

Example: Magnetic Energy in a Coaxial Cable • Derive an expression for the magnetic energy stored in a coaxial cable of length l and inner and outer a and b. The insulation material has magnetic permeability μ.
 Universiti yang menawarkan bidang psikiatri di malaysia
Universiti yang menawarkan bidang psikiatri di malaysia Universiti putra malaysia
Universiti putra malaysia Curtis parry
Curtis parry Ekt kalkulation
Ekt kalkulation 1 jam kredit bersamaan
1 jam kredit bersamaan Gred pensyarah universiti awam
Gred pensyarah universiti awam Universiti teknologi mara akta 173
Universiti teknologi mara akta 173 Contoh ayat mahasiswa
Contoh ayat mahasiswa Malaysia malaysia malaysiansleereuters
Malaysia malaysia malaysiansleereuters Teknologi tenaga perlis consortium
Teknologi tenaga perlis consortium Ckt motor perlis
Ckt motor perlis Keluasan perlis
Keluasan perlis Namakan kawasan tanah pamah
Namakan kawasan tanah pamah Pengasasan kerajaan kedah
Pengasasan kerajaan kedah Perlis thompson principle
Perlis thompson principle Kesultanan perlis
Kesultanan perlis Faclf
Faclf Curl of a vector in cylindrical coordinates
Curl of a vector in cylindrical coordinates Electromagnetic waves obey principle of .. *
Electromagnetic waves obey principle of .. * Electromagnetic theory
Electromagnetic theory Electromagnetic theory
Electromagnetic theory Electromagnetic theory
Electromagnetic theory Electromagnetic theory
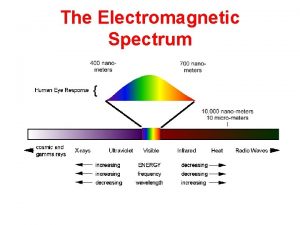
Electromagnetic theory Chapter 18 the electromagnetic spectrum and light
Chapter 18 the electromagnetic spectrum and light Electromagnetic waves vocabulary
Electromagnetic waves vocabulary Similarities of mechanical waves and electromagnetic waves
Similarities of mechanical waves and electromagnetic waves Light waves are electromagnetic waves true or false
Light waves are electromagnetic waves true or false Example of mechanical wave
Example of mechanical wave Electromagnetic energy def
Electromagnetic energy def Differences between mechanical and electromagnetic waves
Differences between mechanical and electromagnetic waves Energy density for electromagnetic wave
Energy density for electromagnetic wave Which colour has the longest wavelength
Which colour has the longest wavelength Electromagnetic star
Electromagnetic star Em waves song lyrics
Em waves song lyrics Conclusion of electromagnetic waves
Conclusion of electromagnetic waves Mechanical waves and electromagnetic waves similarities
Mechanical waves and electromagnetic waves similarities Circular magnetism
Circular magnetism Electromagnetic waves characteristics
Electromagnetic waves characteristics Electromagnetic waves frequency
Electromagnetic waves frequency Orbital notation for chlorine
Orbital notation for chlorine Electromagnetic waves vs mechanical waves
Electromagnetic waves vs mechanical waves Mechanical and electromagnetic waves similarities
Mechanical and electromagnetic waves similarities Electromagnetic spectrum foldable
Electromagnetic spectrum foldable Electromagnetic waves: seeing objects and color
Electromagnetic waves: seeing objects and color Electromagnetic waves chart
Electromagnetic waves chart Mnemonic for electromagnetic spectrum
Mnemonic for electromagnetic spectrum Attracted armature relay
Attracted armature relay Radiation powerpoint template free
Radiation powerpoint template free Electromagnetic spectrum micrometers
Electromagnetic spectrum micrometers Electromagnetic induction ppt
Electromagnetic induction ppt F=qvb
F=qvb Definition of emc
Definition of emc Design and fabrication of electromagnetic braking system
Design and fabrication of electromagnetic braking system Electromagnetic spectrum mnemonic
Electromagnetic spectrum mnemonic Electromagnetic spectrum foldable
Electromagnetic spectrum foldable Intensity in em wave
Intensity in em wave Electromagnetic oscillation pdf
Electromagnetic oscillation pdf Em waves formulas
Em waves formulas Electromagnetic log
Electromagnetic log Rays chart
Rays chart Is a seismic wave mechanical or electromagnetic
Is a seismic wave mechanical or electromagnetic Kesler science sound waves answer key
Kesler science sound waves answer key Two technicians are discussing electromagnetic induction
Two technicians are discussing electromagnetic induction Electromagnetic power formula
Electromagnetic power formula