Lecture 2 Electromagnetic Theory Photons and Light 2





















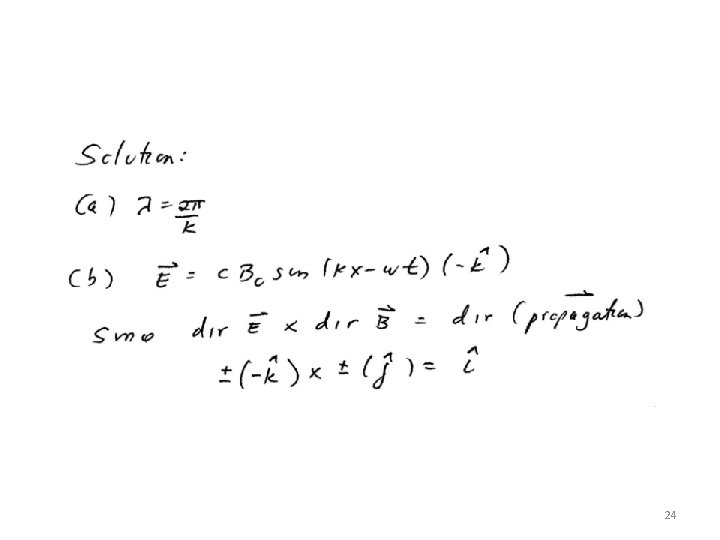




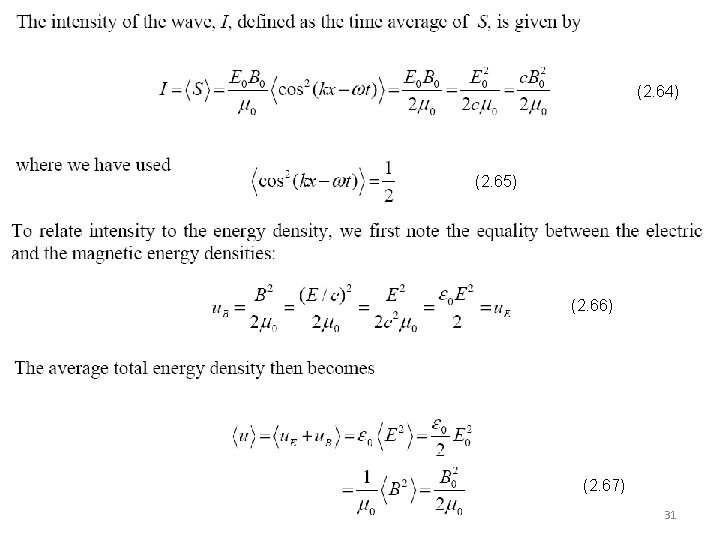








- Slides: 39

Lecture 2 Electromagnetic Theory, Photons, and Light 2. 0 Introduction 2. 1 Basic laws of electromagnetic theory In this section we will review and develop, briefly some of the ideas needed to appreciate the concept of electromagnetic waves. We will see that light is a form of electromagnetic radiation so it is instructive to review some of the properties of electricity and magnetism. The original studies of electricity and magnetism date back to at least the early Greek times. By the start of the nineteenth century, it was known that some objects could posess an electrical charge, and then these charges could exert a force on each other even though in a vacuum. This force could be described mathematically as Where q is the electrical charge on the object in question and is the electrical field produced by all other charges in the universe 1

In addition it was also noted that a moving charge may experience another force always proportional to its velocity magnetic induction which is . We are thus led to define yet another field, namely the , such that . If both forces and occur concurrently the charge is said to be moving through a region pervaded by both electric and magnetic fields, where upon. There are several other observations which may be interpreted in terms of these fields and in so doing we can get a better idea of the physical properties which must be attributed to and . As we shall see electric fields are generated by both electric charges and by time-varying magnetic fields. Similarly, magnetic fields are generated by electric currents and time-varying electric fields. This independence of and is a keypoint in the description of light and its elaboration is the motivation for much of what is to follow. 2

2. 1. 1 Faraday Induction Law Michael Faraday made a number of major contributions to electromagnetic theory, one of the most significant of which was his discovery that a time-varying magnetic flux, passing through a closed conducting loop, results in the generation of a current around that loop. Demonstration: The flux of the magnetic induction(or magnetic flux density) through any open area A, bounded by conducting loop is given by The induced electromotive force or emf developed around the loop is then Indeed, the emf exists only as a result of the presence of an electric field given by 3

Equating equations (2. 2) and (2. 3), and making used of Eq 2. 1 we get The path can be chosen quite arbitrarily and need not be within, or anywhere near a conductor. The electric field in Eq 2. 4 does not arise directly from the presence of electric charges but rather from the time-varying magnetic field. With no charges to act as sources or sinks, the fields lines close on themselves, forming loops. For the case in which the path is fixed in the space and unchanging in shape, the induction law (Eq 2. 4) can be rewritten as This expression indicates that a time-varying magnetic field will have an electric field associated with it. 4

2. 1. 2 Gauss’s Law-Electric Another of the fundamental laws of electromagnetism is named after the german mathematicien Karl Friedrich Gauss. It relates the flux of the electric field intensity through a closed surface A to a total enclosed charge. The circled double integral is meant to serve at a reminder that the surface is closed. If the volume enclosed by A is V, and if within it there is a continuous charge distribution of density then Gauss’s law is The integral on the left is the difference between the amount of flux flowing into, and out of, any closed surface A. If there is a difference, it will be due to the presence of sources or sinks of the electric field within A. The constant є is known as the electric permittivity of the medium. For the special case of vacuum, the permittivity of free space is given by 5

The permittivity of a material is given by , where Ke the dielectric constant (or relative permittivity), is a dimensionless quantity, and is the same for all systems of units. 2. 1. 3 Gauss’s Law-Magnetic There is no known counterpart to the electric charge, i. e no magnetic poles have ever been found. Unlike the electric field, the magnetic induction does not diverge from or converge toward some king of magnetic charge (a monopole source or sink) A flux on magnetic induction through a closed surface is zero, and we have the magnetic equivalent of Gauss’s law 2. 1. 4 Ampere’s Circuital Law Another equation which will be of great interest to us is due to Andre Marie Ampere, known as the circuital Law, it relates line integral of tangent to a closed curve C, with total current i passing within the confines of C. 6

The open surface A is bounded by C and J is the current per unit area. The quantity µ is called the permeability of the particular medium. For the vacuum (the permeability of the free space ) which is defined as With Km being the dimensionless relative permeability. Equation (2. 9), although often adequate, is not the whole truth, Maxwell hypothesized the displacement current density defined by And restated the Ampere’s Law as: It points out that even when , the time-varying field will be accompanied by a field. 7

2. 1. 5 Maxwell’s Equations The set of integral expressions given by equations (2. 5), (2. 7), (2. 8) and (2. 12) have come to be known as Maxwell’s equations. Remember that these are generalizations of experimental results. The very simplest statement of Maxwell’s equations governs the behavior of the electric and magnetic fields is free space where , and both ρ and are zero. In that instance Observe that except for a multiplicative scalar, the electric and magnetic fields appear in the equations with a remarkable symmetry. However affects , will in turn affect . The mathematical symmetry implies a good deal of physical symmetry 8

Maxwell’s equations can be written in a differential form which will be more useful for our purpose, using the gauss’s divergence theorem And the Stokes theorem Applying Stokes theorem to the electric field intensity we have Upon comparing this with equation (2. 5) it follows that This result must be true for all surfaces bounded by path C. This can only be the case if the integrands are themselves equal, i. e if 9

A similar application of stokes theorem to Note: using Equation (2. 12) results in is the Ohm’s law so Gauss’s divergence theorem applied to electric field intensity yields If we make use of Equation (2. 7) this becomes And since this is to be true for any volume, the two integrands must be equal. Consequently, at any point (x, y, z) is space-time. In the same fashion Gauss’s divergence theorem applied to field and combine with Equation (2. 8) yields 10

Equations (2. 21), (2. 22), (2. 25) and (2. 26) are Maxwell’s equations in differential form. For simple case of Cartesian coordinates and free space , , The Maxwell’s equations are given by 11

The transition has thus been made from the formulation of Maxwell’s equations in terms of integrals over finite regions, to restatement in terms of derivatives at points in space. We now have all that is needed to comprehend the magnificent process whereby electric and magnetic fields, inseparably coupled, and mutually sustaining, propagate out into space as a single entity, free of charges and currents, sans matter, sans ether. 12

2. 2 electromagnetic waves Maxwell’s Equations for free space are as follow: These equations can be manipulated into the form of two vector representations: Taking the curl of equation (2. 31) we have Making use of (eq 2. 33) 13

Making use of (eq 2. 31) Equating L. H. S and R. H. S we have (2. 35) Similarly we have (2. 36) The Laplacien operates on each component of and so that the two vector equations actually represent a total of six scalar equations. Two of these expressions, in Cartesian coordinates are We can have precisely the same from , , , and . Equations of this exact sort, which relate the space and time variations at some physical quantity , had been studied long 14 before Maxwell work and were known to describe wave phenomena.

Each and every component of the electromagnetic field ( ) therefore obeys the scalar differential wave equation Provided that Maxwell evaluated v and found out that in free space, the speed of all electromagnetic wave is: (2. 40) This theoretical value was in remarkable agreement with the previously measured speed of light determined by Fizeau and this led Maxwell to comment that: The velocity is so nearly that of light , that it seems we have strong reason to conclude that light itself is an electromagnetic disturbance in the form of waves propagating through the electromagnetic field according to electromagnetic laws. 15

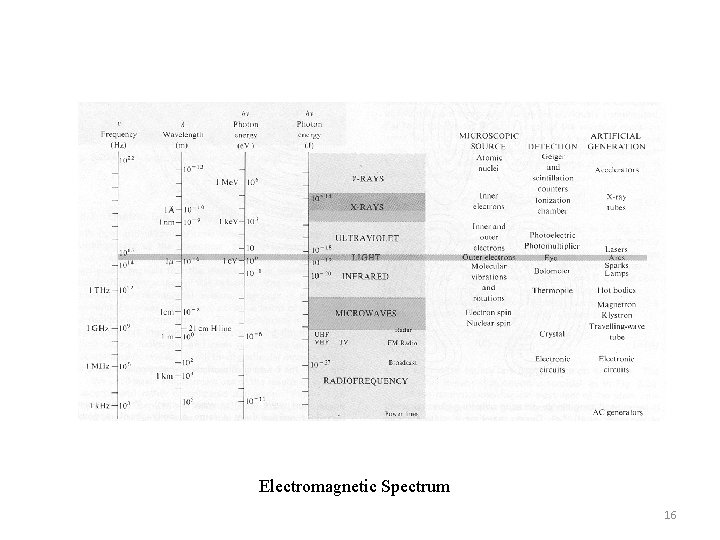
Electromagnetic Spectrum 16

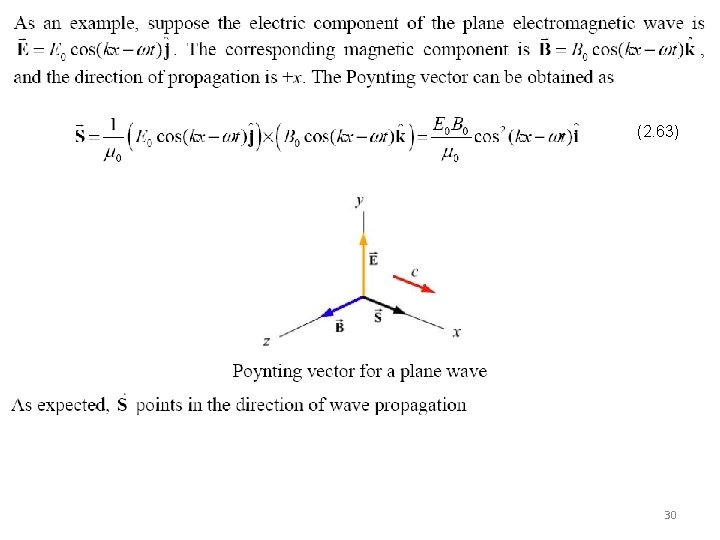
It has become customary to designate the speed of light in vacuum by the symbol C, the presently accepted value of which is 2. 3 Transverse character of light Let’s consider for simplicity an electromagnetic wave propagating in the +x-direction, with the electric field pointing in the +y direction and the magnetic field in the +z direction, as shown in the figure below: A plane electromagnetic wave 17

It was experimentally verified that light has a transverse character. Now we will explain it in the context of the electromagnetic theory. To that end, consider the fairly simple case of a plane wave propagating in the positive x-direction as shown in the figure above: The electric field is a solution of equation (2. 35) where is constant over each one of an infinite set of planes perpendicular to the x-axis. It is therefore only a function of x and t, i. e. We now refer back to Maxwell’s equations, and particular to equation (2. 33) which is generally read as the divergence of equal zero. Since is not a function of either y or z, the equation reduces to The component of the electric field in the x-direction. i. e in the direction of propagation, is constant. The electric field associated with the plane wave is the exclusively transverse. The electric field is parallel to the y-axis where upon 18

Returning to the set of equation (2. 27), it follows that And that and are constant, and therefore of no present interest. The time-dependent field can only have a component in the z-direction. Clearly then, in free space, the plane electromagnetic wave is indeed transverse as shown in the figure below Orthogonal harmonic -field and -field 19

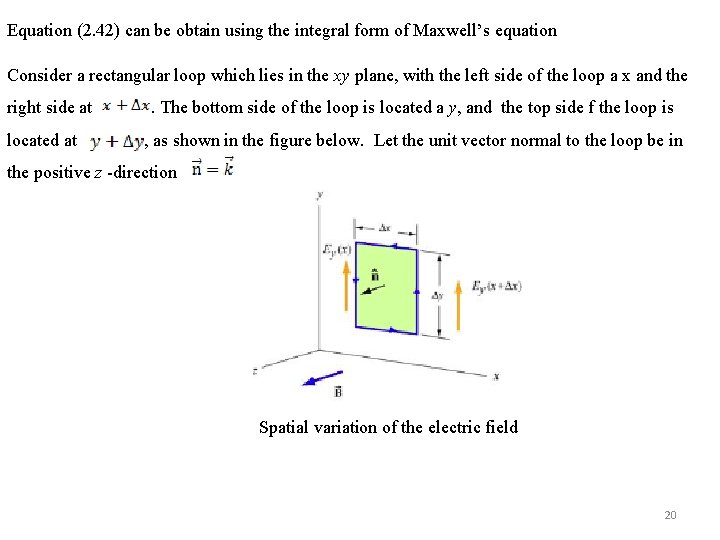
Equation (2. 42) can be obtain using the integral form of Maxwell’s equation Consider a rectangular loop which lies in the xy plane, with the left side of the loop a x and the right side at located at . The bottom side of the loop is located a y, and the top side f the loop is , as shown in the figure below. Let the unit vector normal to the loop be in the positive z -direction Spatial variation of the electric field 20

Using Faraday’s law The L. H. S can be written as: Where we have made the expansion On the other hand, the rate of change of the magnetic flux on the right-hand -side is given by Equating the two expressions and dividing by the area yields We have not specified the form of the disturbance other than to say it was a plane wave. Our conclusions are therefore quite general, applying equally well to pulses or continuous waves. We therefore limit the discussion to harmonic waves and write as 21

The speed of propagation being c. The associated magnetic flux density can be found by directly integrating equation (2. 42) that is: Using equation (2. 43) we obtain or The constant of integration, which represents a time-independent has been disregarded. On comparing with equation (2. 43), it is evident that: Since and differ only by a scalar, and so have the same time-dependence in phase at all points in space. and are

Moreover, and are mutually perpendicular and their cross points in the direction of propagation Activity 2. 1 23
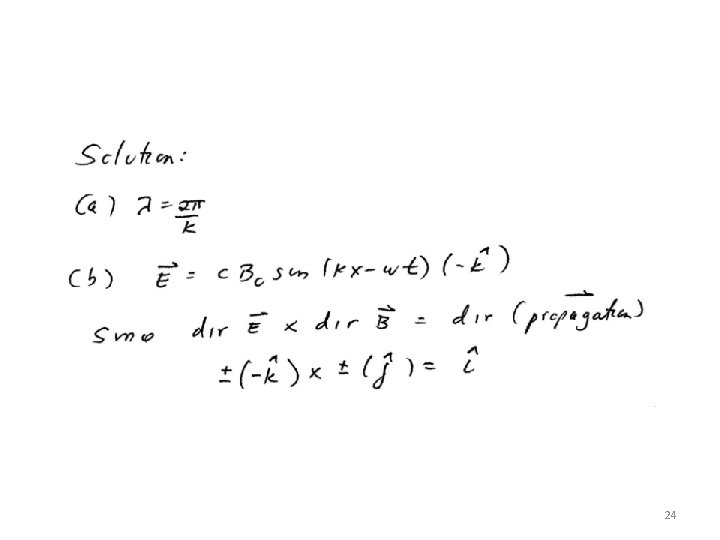
24

2. 3 Standing electromagnetic waves (2. 48) (2. 49) (2. 50) (2. 51) 25

(2. 52) (2. 53) One may verify that the fields and ( [ eq 2. 52 and 2. 53)] still satisfy the wave equation stated in equation (2. 35) and (2. 36), even though they no longer have the form of the functions of . These waves [ eq 2. 52 and 2. 53)] are standing wave, which do not progate. 26

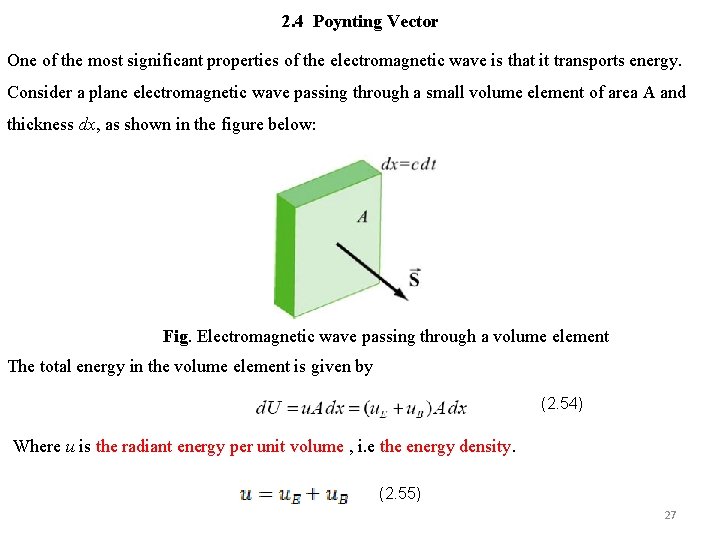
2. 4 Poynting Vector One of the most significant properties of the electromagnetic wave is that it transports energy. Consider a plane electromagnetic wave passing through a small volume element of area A and thickness dx, as shown in the figure below: Fig. Electromagnetic wave passing through a volume element The total energy in the volume element is given by (2. 54) Where u is the radiant energy per unit volume , i. e the energy density. (2. 55) 27

u. E and u. B are the electric and magnetic field energy density respectively. For the electric field alone can compute the energy density to be: (2. 56) Similarly, the energy density for the magnetic field alone is (2. 57) Using equations (2. 56) and (2. 57) we can rewrite equation (2. 54) as (2. 58) Since the (2. 59) 28

(2. 60) (2. 61) (2. 62) 29

(2. 63) 30
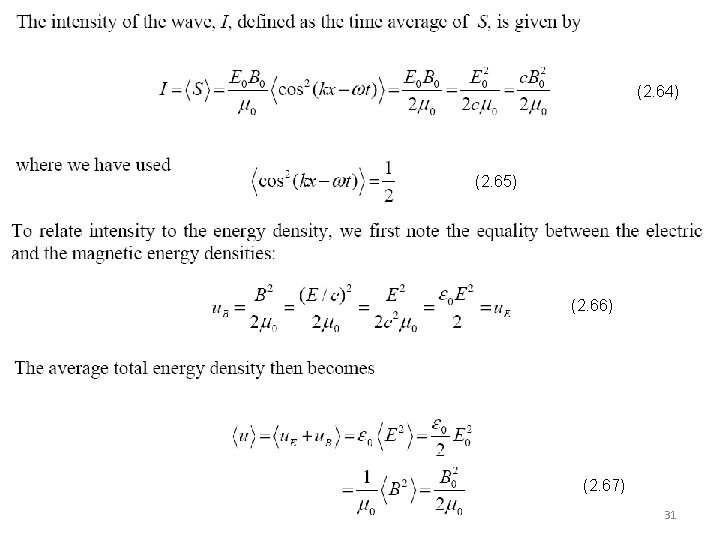
(2. 64) (2. 65) (2. 66) (2. 67) 31

(2. 68) Activity 2. 2: Solar constant 32

Solution Activity 2. 2: Solar constant 33

34

Solution Activity 2. 3: Intensity of a standing wave 35

36

2. 4 Momentum Suppose a light wave passing by, and interacting with an electron at some instant in time. The electric fields exerts a force which drives the electron with a velocity magnetic field, in turn, exerts a force Although changes its direction as . The . varies, remaining aniparallel to always in the direction of propagation, since and at all times, is reverse directions simultaneously. The electron undergoes both rapid transverse oscillation, at the frequency of the wave, and a very slight increase in speed in the direction in which the light propagates. The effect of this small additional component of the velocity, arising from the magnetic field, is quite negligible. We are interested in determining the amount of linear momentum delivered to the electron by the field. The total force acting on the electron is and its time-averaged value is 37

Where is oscillatory and average to zero. The magnitudes of and are related by and so If W is the instantaneous work done on the electron by the wave, then the rate at which work is being done is Thus, on the average Notice that . Comparing this to Ep(2. 71) gives And using the fact that the rate of change of momentum equals the force, we have 38

Over some interval in time, during which the electron removes an amount of energy E from the light wave, it will also take an amount of momentum equal , in the direction of the propagation. In the photon picture, a particle-like quanta have an energy . We can then expect a photon to carry a momentum The relativity relates the rest mass mo, energy and momentum of a particle by way of For a photon mo=0 and If and electromagnetic wave impinges on an object and is absorbed or reflected, momentum will be imparted to the electron within the material and subsequently transmitted to the lattice structure of the object as a whole. The average rate of transfer of momentum per unit area, is known as the radiation pressure P. In the special case of normal incidence and complete absorption of the incoming light, it can be shown that 39
 Gabriela barreto lemos
Gabriela barreto lemos Do photons have momentum
Do photons have momentum What are photons made of
What are photons made of Facts about photons
Facts about photons Photons
Photons Light light light chapter 23
Light light light chapter 23 Into the light chapter 22
Into the light chapter 22 Chapter 22
Chapter 22 Chapter 18 electromagnetic spectrum and light
Chapter 18 electromagnetic spectrum and light Radio wave to gamma ray
Radio wave to gamma ray 01:640:244 lecture notes - lecture 15: plat, idah, farad
01:640:244 lecture notes - lecture 15: plat, idah, farad Light is an electromagnetic wave true or false
Light is an electromagnetic wave true or false Orbital notation of chlorine
Orbital notation of chlorine Light electromagnetic
Light electromagnetic Light electromagnetic
Light electromagnetic Divergence in electromagnetic theory
Divergence in electromagnetic theory Energy density of electromagnetic waves
Energy density of electromagnetic waves Electromagnetic theory
Electromagnetic theory Electromagnetic theory
Electromagnetic theory Electromagnetic theory
Electromagnetic theory Electromagnetic theory
Electromagnetic theory Put out the light, and then put out the light
Put out the light, and then put out the light Membrane bound organelles
Membrane bound organelles The bouncing off of light
The bouncing off of light Natural language processing
Natural language processing Decision theory lecture notes
Decision theory lecture notes Sargur srihari
Sargur srihari Natural language processing lecture notes
Natural language processing lecture notes Things that blocks light
Things that blocks light Transverse waves move perpendicular
Transverse waves move perpendicular Energy that travels through
Energy that travels through Mechanical waves and electromagnetic waves similarities
Mechanical waves and electromagnetic waves similarities Difference between matter waves and electromagnetic waves
Difference between matter waves and electromagnetic waves Mechanical vs electromagnetic waves
Mechanical vs electromagnetic waves Mechanical and electromagnetic waves similarities
Mechanical and electromagnetic waves similarities Electromagnetic waves seeing objects and color
Electromagnetic waves seeing objects and color Electromagnetic oscillations and alternating current
Electromagnetic oscillations and alternating current Electromagnetic oscillations and alternating current
Electromagnetic oscillations and alternating current Alternating current circuits and electromagnetic waves
Alternating current circuits and electromagnetic waves Mechanical and electromagnetic waves
Mechanical and electromagnetic waves