Tiing Error Correction Experiments Chen HoLin Chen Nov

Tiing Error Correction & Experiments. Chen Ho-Lin Chen Nov 8 2005 (Chen)

Self-Assembly n Self-Assembly is the process by which simple objects autonomously assemble into complexes. n n Goals: Understand self-assembly, design self-assembling systems n (Chen) Geometry, dynamics, combinatorics are all important Inorganic: Crystals, supramolecules Organic: Proteins, DNA, cells, organisms A key problem in nano-technology, molecular 2

Applications of Self-Assembly n Building blocks of nano-machines. n DNA computing. n n (Chen) Small electrical devices such as FLASH memory. [Black et. Al. ’ 03] Nanostructures which “steer” light in the same way computer chips steer electrons. [Percec et. Al. ’ 03] 3

Self-Assembly of DNA (Chen) [Winfree] 4

Abstract System Model (Chen)

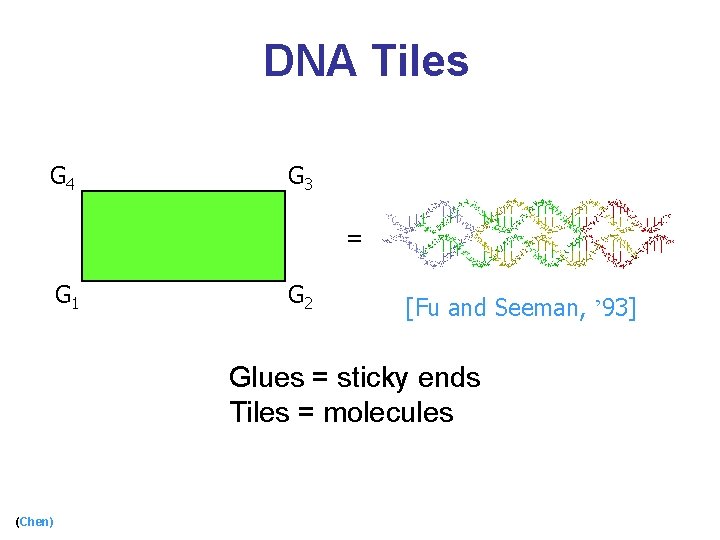
DNA Tiles G 4 G 3 = G 1 G 2 [Fu and Seeman, ’ 93] Glues = sticky ends Tiles = molecules (Chen)

abstract Tile Assembly Model: [Rothemund, Winfree, ’ 2000] Temperature: A positive integer. (Usually 1 or 2) A set of tile types: Each tile is an oriented rectangle with glues on its corners. Each glue has a non-negative strength (0, 1 or 2). An initial assembly (seed). x x (Chen) y z A tile can attach to an assembly iff the combined strength of the “matched glues” is greater or equal than the temperature. 7

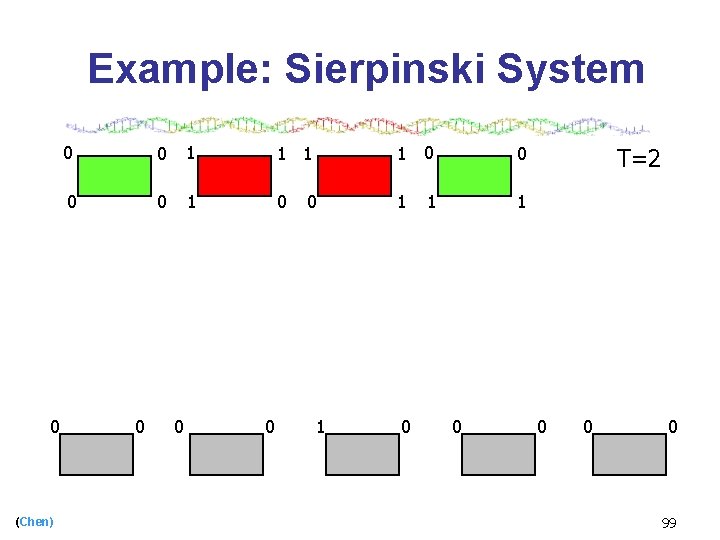
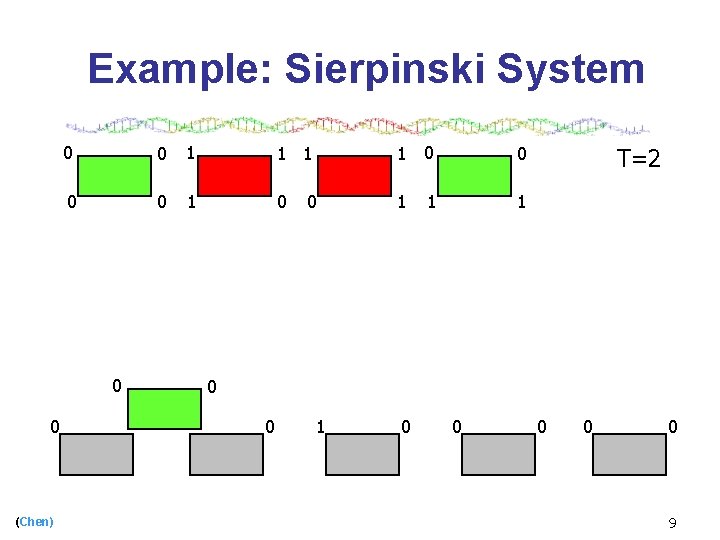
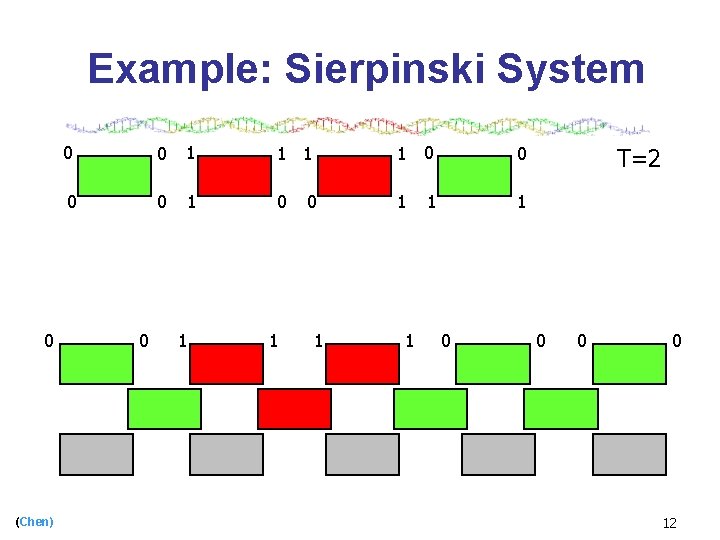
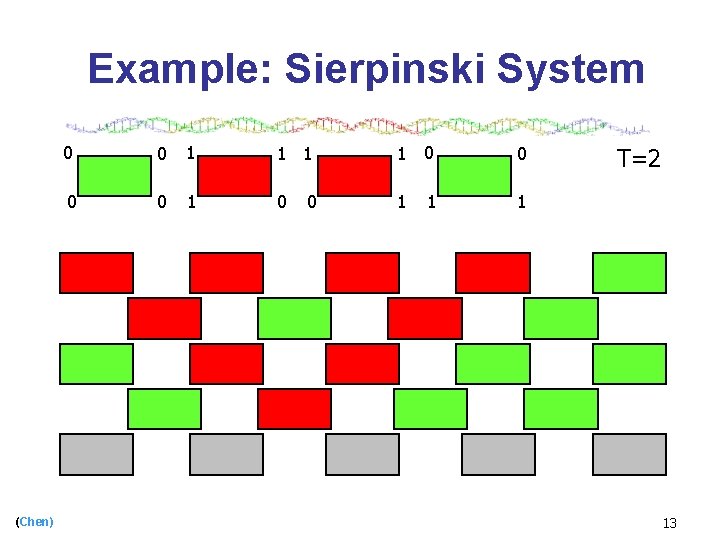
Example: Sierpinski System [Winfree, ’ 96] 0 (Chen) 0 0 1 1 0 0 1 0 T=2 0 0 0 8

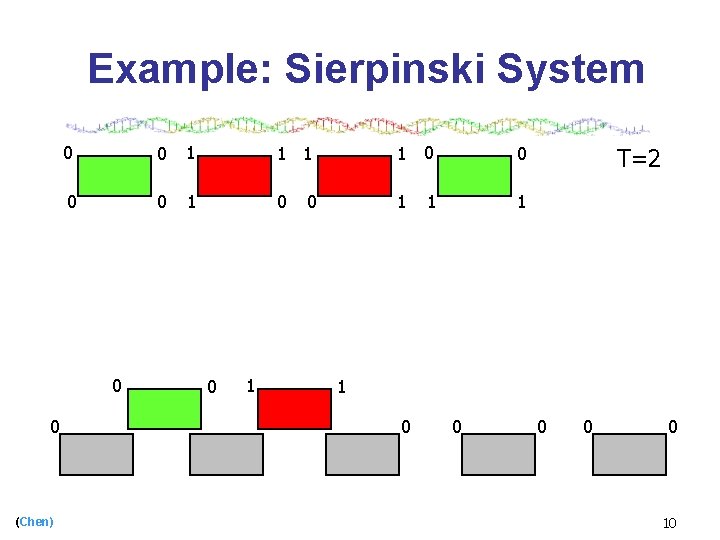
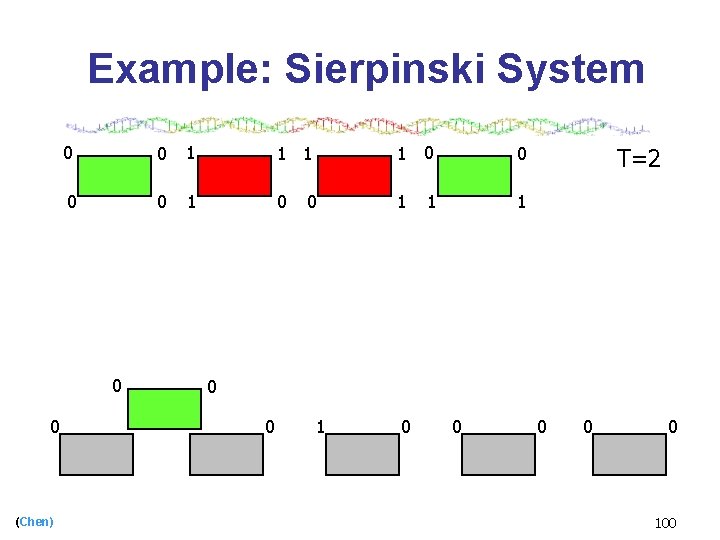
Example: Sierpinski System 0 0 1 1 0 0 1 0 1 1 0 0 (Chen) 0 1 T=2 0 0 1 0 0 0 9

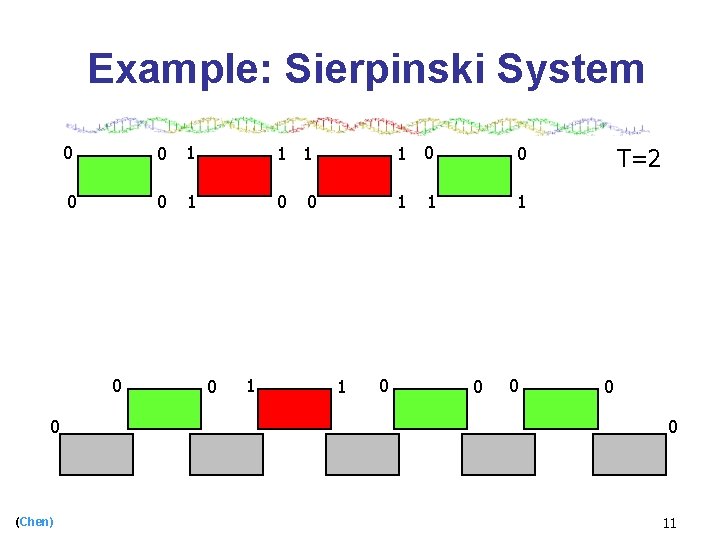
Example: Sierpinski System 0 0 1 1 0 0 1 0 1 1 0 0 (Chen) 0 1 T=2 1 0 0 0 10

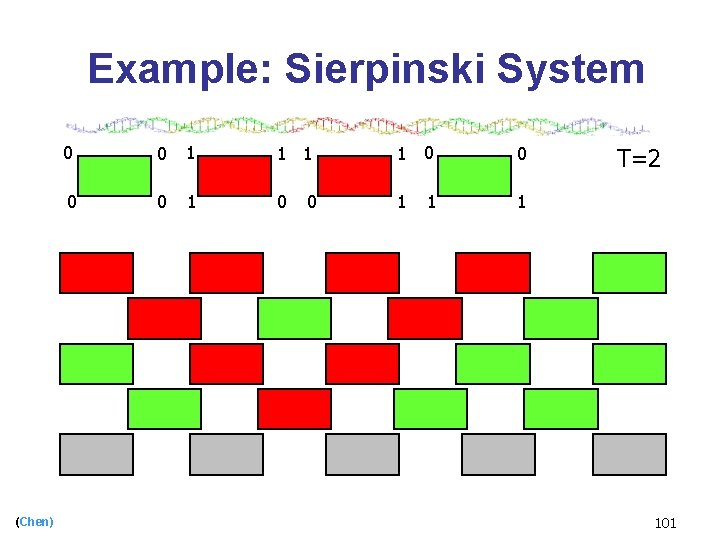
Example: Sierpinski System 0 0 1 1 0 0 1 0 1 1 0 0 (Chen) 0 1 0 1 0 0 T=2 0 0 11

Example: Sierpinski System 0 (Chen) 0 0 1 1 0 0 1 0 1 1 1 0 T=2 0 0 0 12

Example: Sierpinski System (Chen) 0 0 1 1 0 0 1 0 1 T=2 13

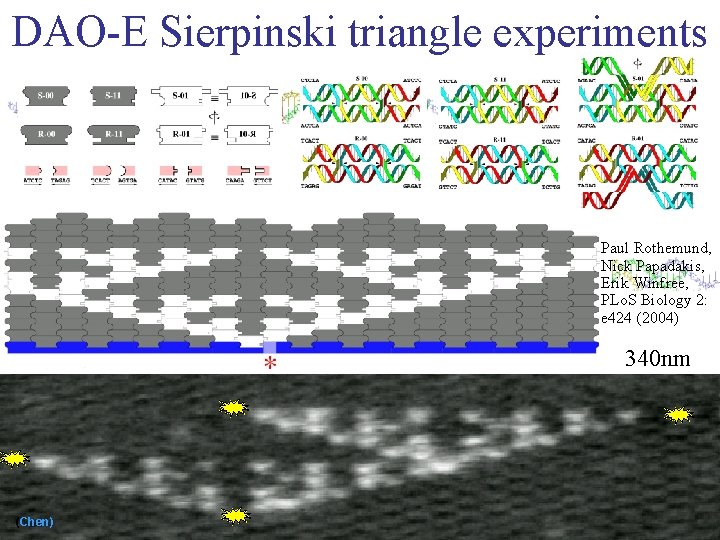
DAO-E Sierpinski triangle experiments Paul Rothemund, Nick Papadakis, Erik Winfree, PLo. S Biology 2: e 424 (2004) 340 nm (Chen)

Theoretical Results n Efficiently assembling basic shapes with precisely controlled size and pattern. n n Constructing N X N squares with O(log n/log n) tiles. [Adleman, Cheng, Goel, Huang, ’ 01] Perform universal computation by simulating BCA. [Winfree ’ 99] n (Chen) Assemble arbitrary shape by O( Kolmogorov complexity) tiles with scaling. [Soloveichik, Winfree ’ 04] 15

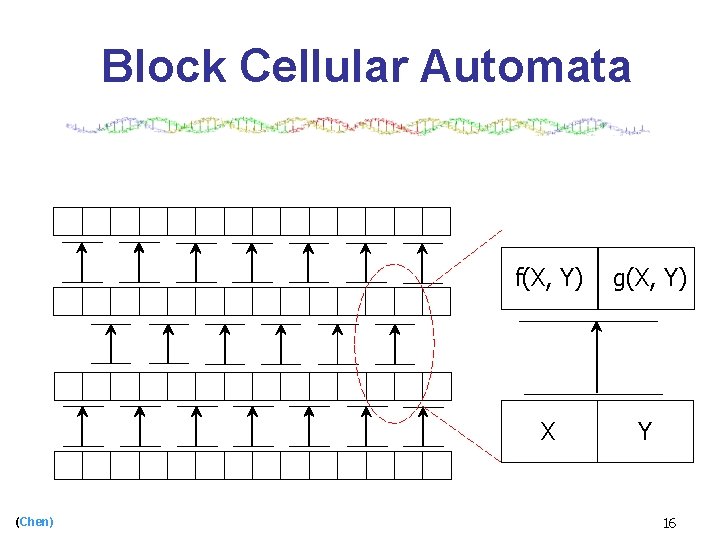
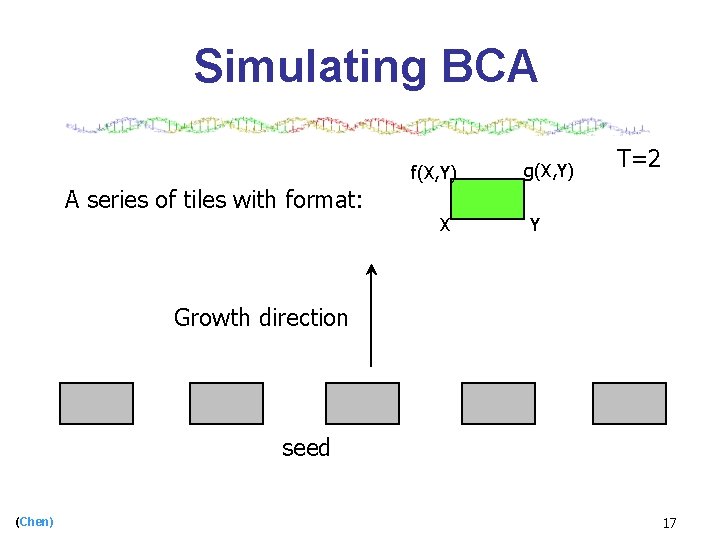
Block Cellular Automata (Chen) f(X, Y) g(X, Y) X Y 16

Simulating BCA f(X, Y) g(X, Y) T=2 A series of tiles with format: X Y Growth direction seed (Chen) 17

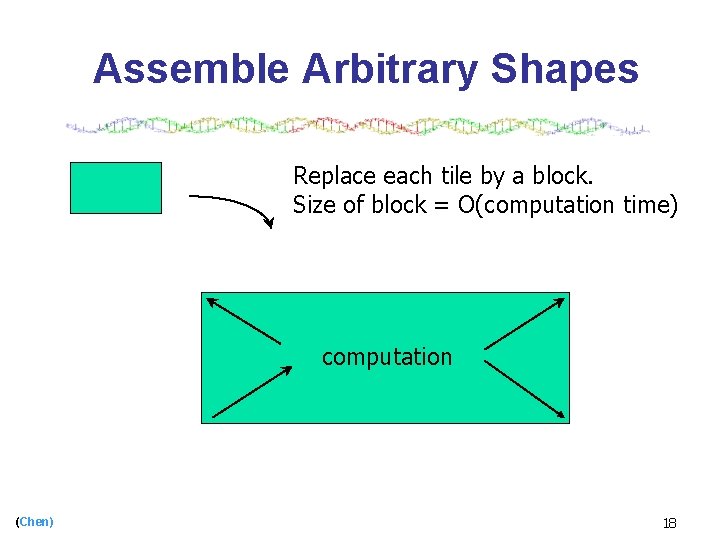
Assemble Arbitrary Shapes Replace each tile by a block. Size of block = O(computation time) computation (Chen) 18

Tile System Design n Library of primitives to use in designing nano-scale structures [Adleman, Cheng, Goel, Huang, ’ 01] n Automate the design process [Adleman, Cheng, Goel, Huang, Kempe, Moisset de espanes, Rothemund ’ 01] (Chen) 19

Kinetic System Model (Chen)

kinetic Tile Assembly Model: [Winfree, 1998] A tile can attach at any location. The rate of attachment rf = constant. The rate of detachment rr, b = c e-b. G (Chen) 21

Kinetic model => Abstract model n We set the temperature and concentration to rr, T+1 << rr, T < rf << rr, T-1 n n (Chen) If a tile attaches with strength < T-1, it is likely to fall off very fast. If a tile is held by strength at least T+1, it is unlikely to fall off 22

Error Correction

Robustness Designs n Use biological mechanisms in the process. n n Add extra structure/modification on the process of DNA self-assembly. Add combinatorial structures to tile systems. n Use the original erroneous process, but add more structure to the tile system to do error correction. 24

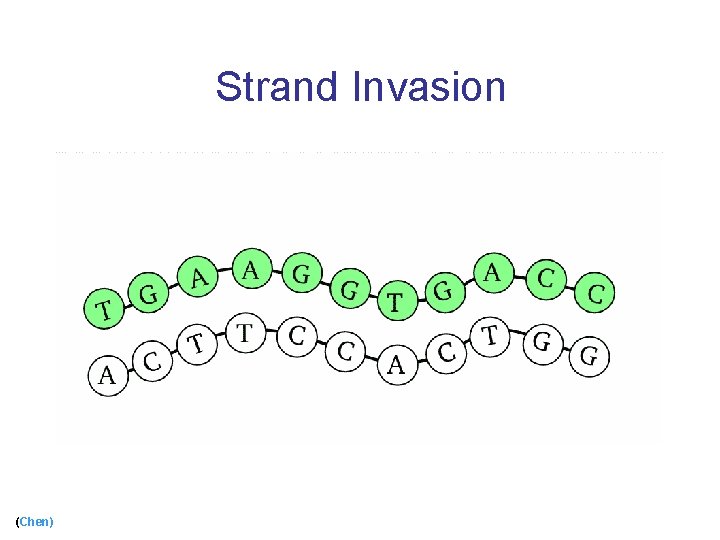
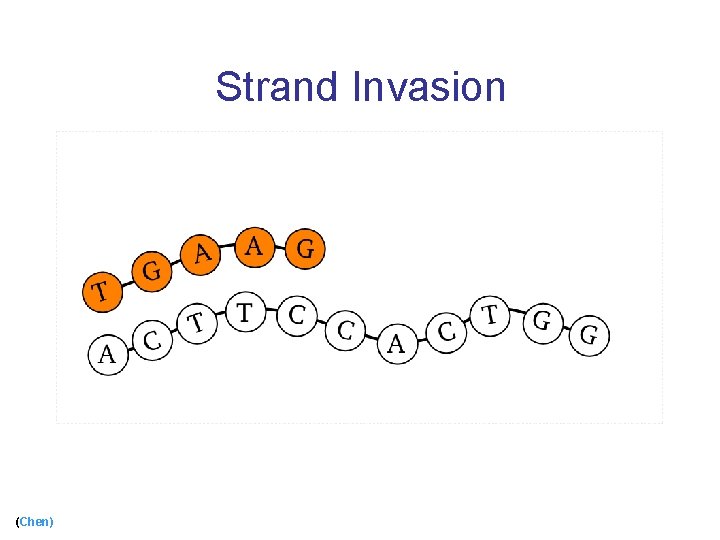
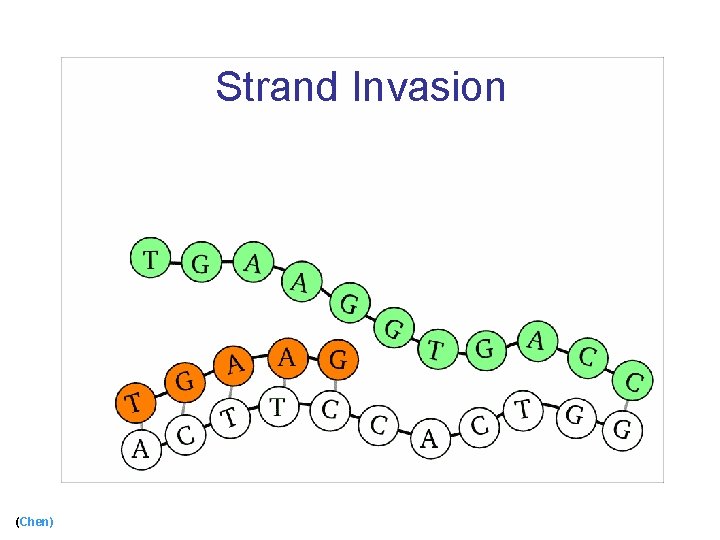
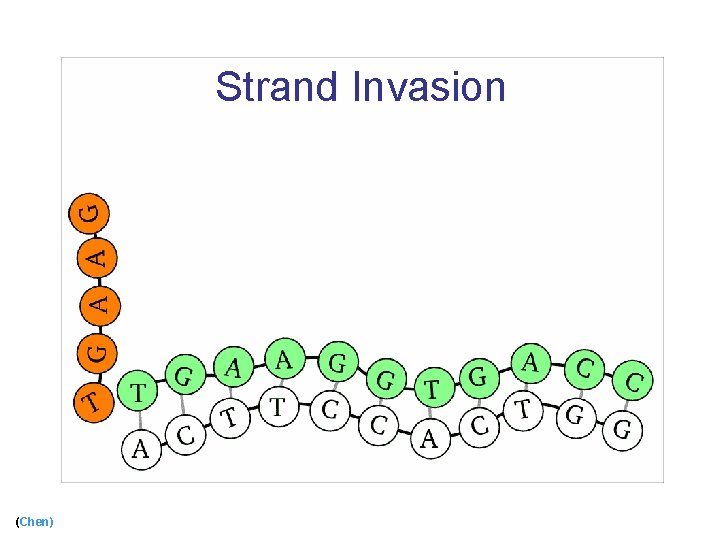
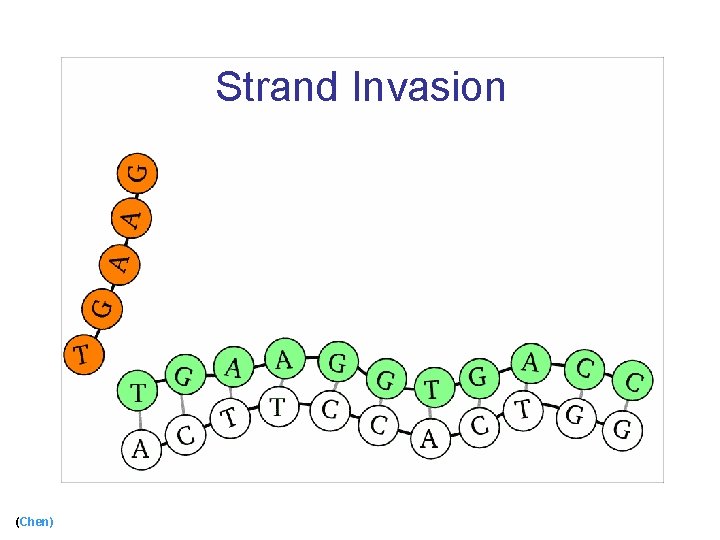
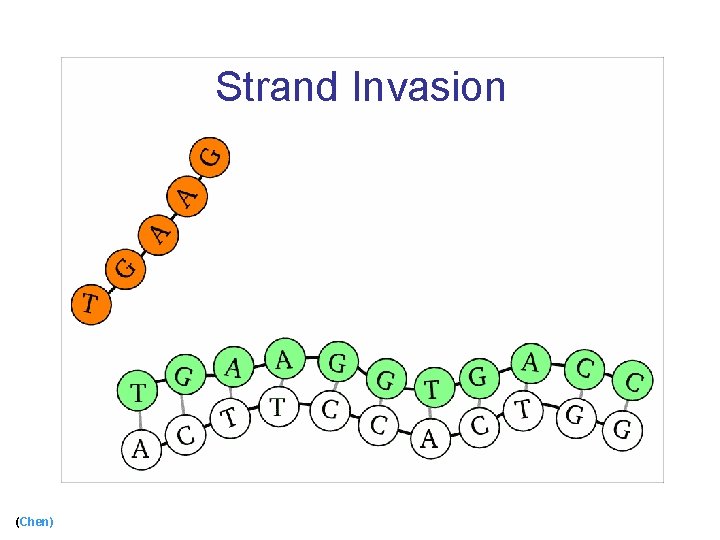
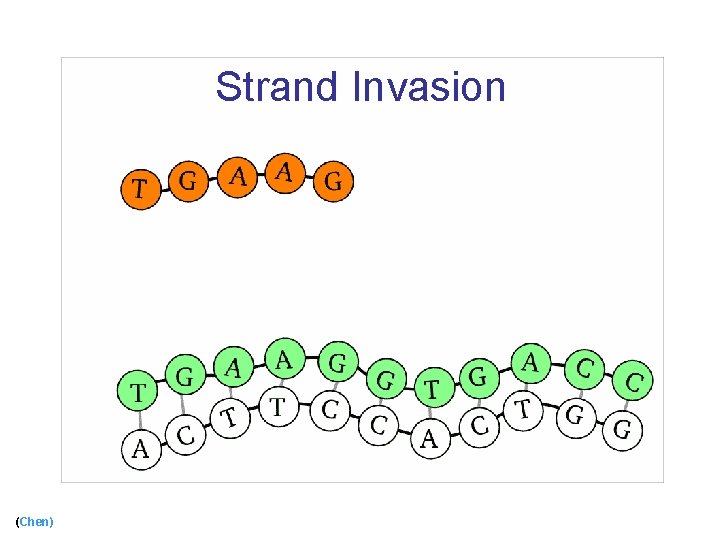
Using Biological Mechanisms n Use strand invasion [Chen, Cheng, Goel, Huang, Moisset de espanes, ’ 04] n Add protecting tiles [Fujibayashi and Murata, ’ 04] (Chen) 25

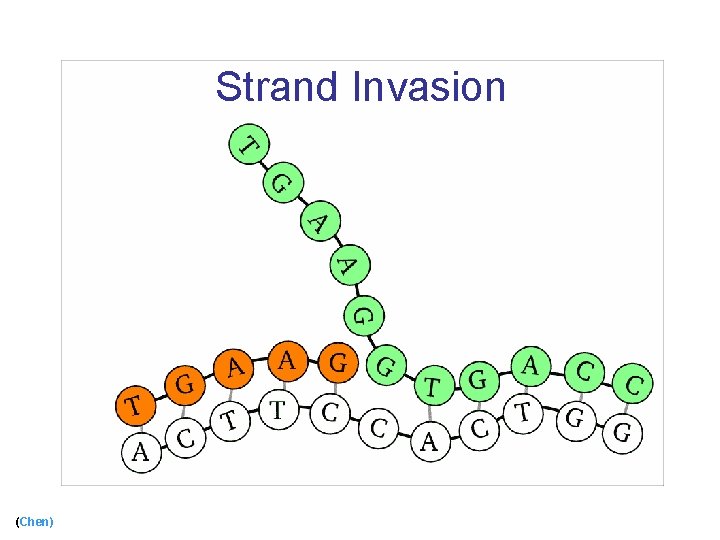
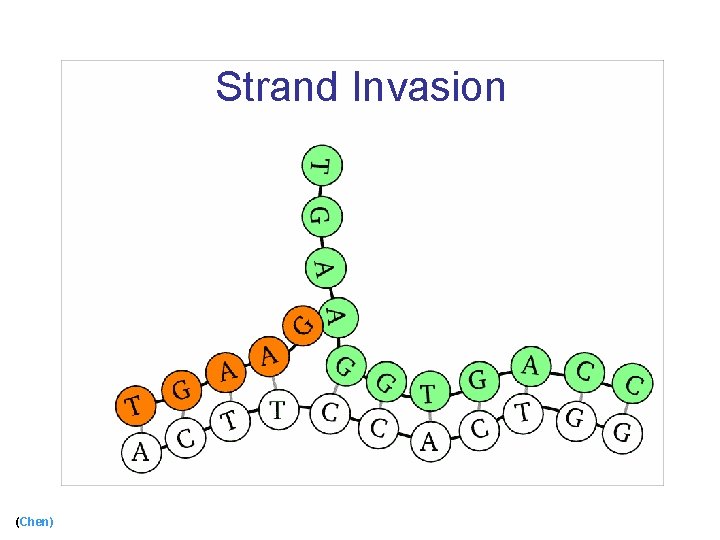
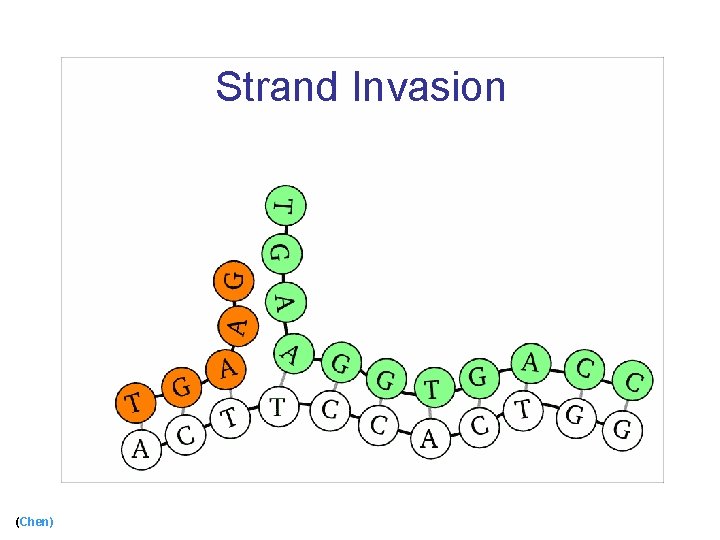
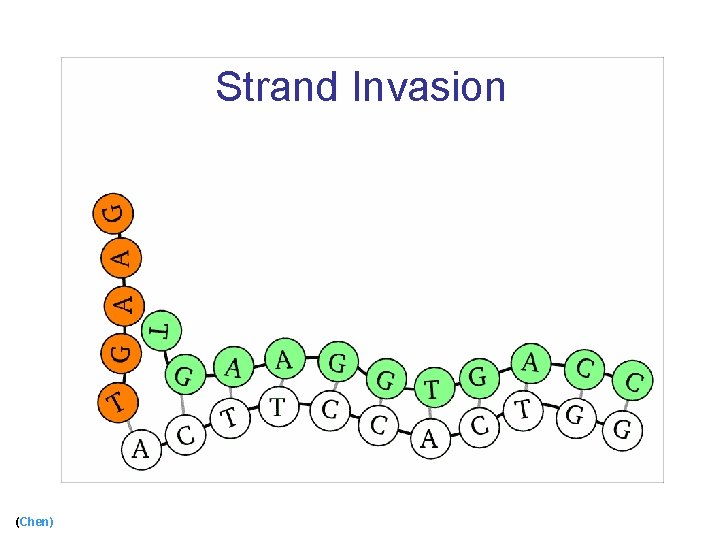
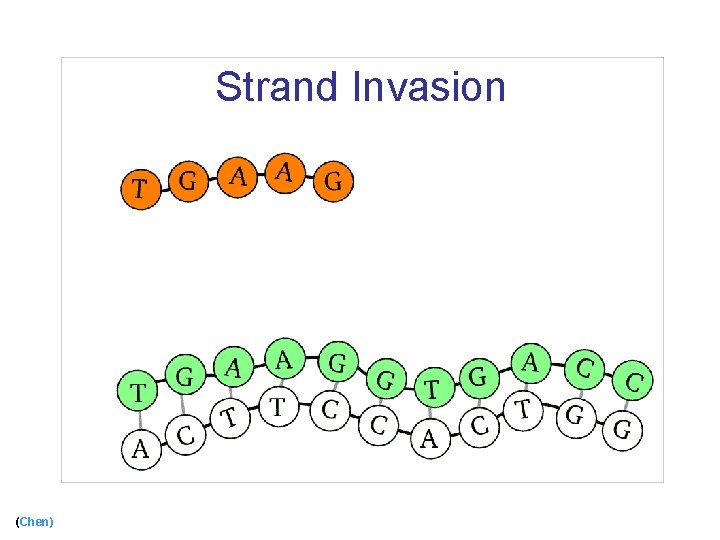
Strand Invasion (Chen)

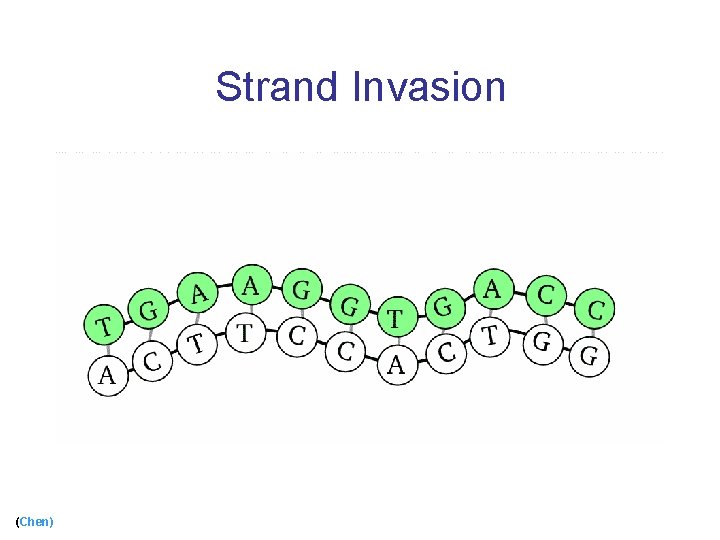
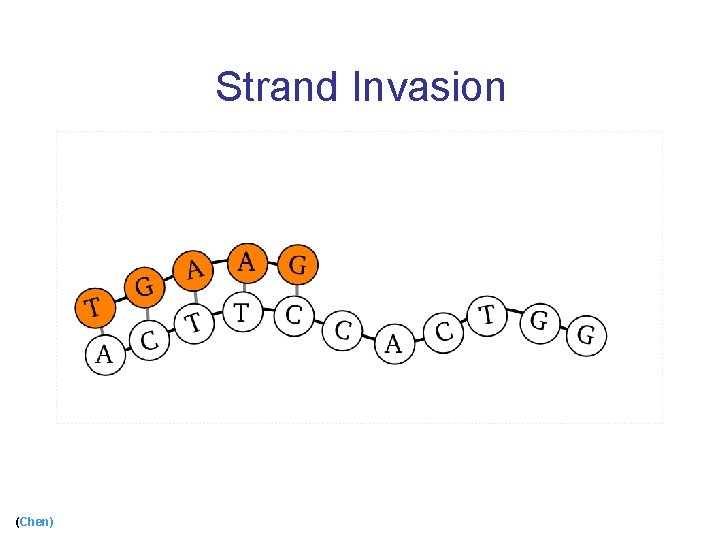
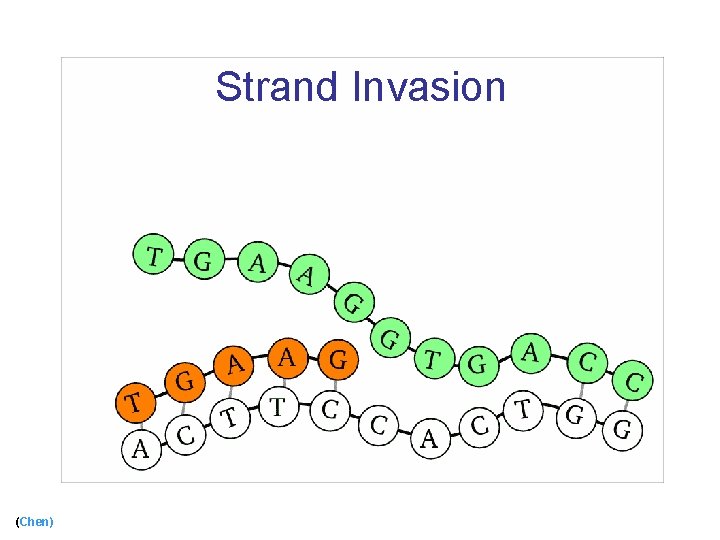
Strand Invasion (Chen)

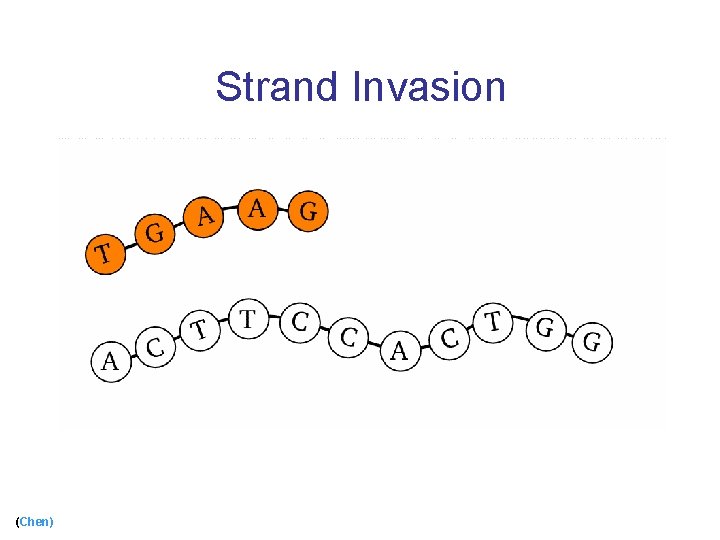
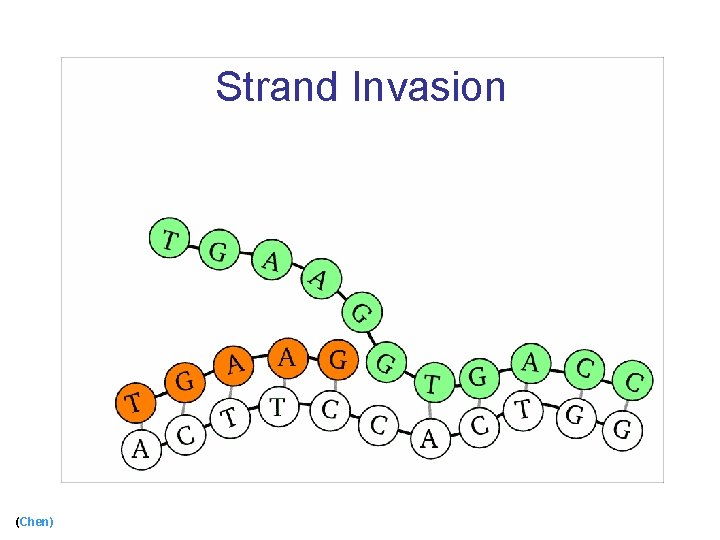
Strand Invasion (Chen)

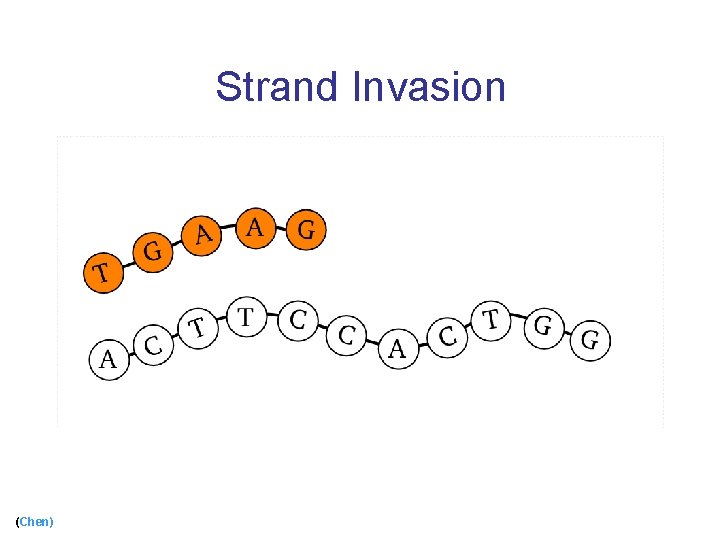
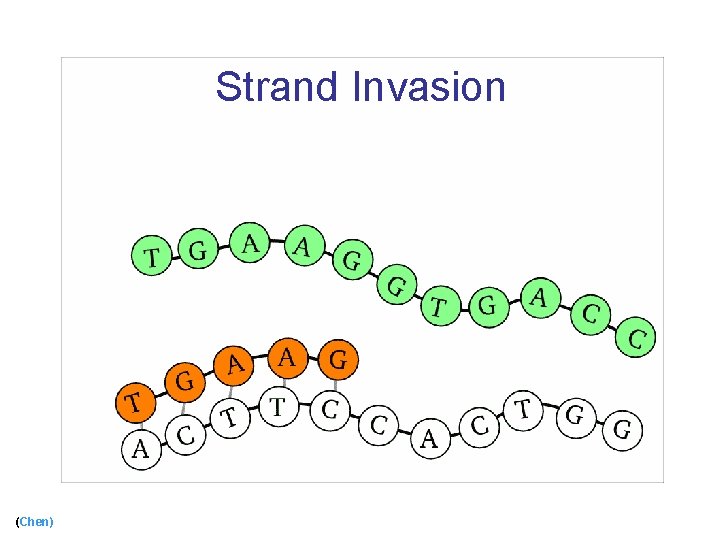
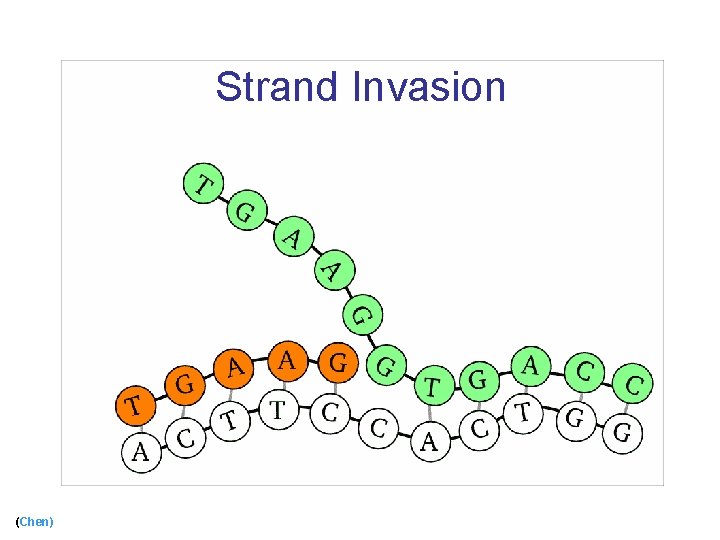
Strand Invasion (Chen)

Strand Invasion (Chen)

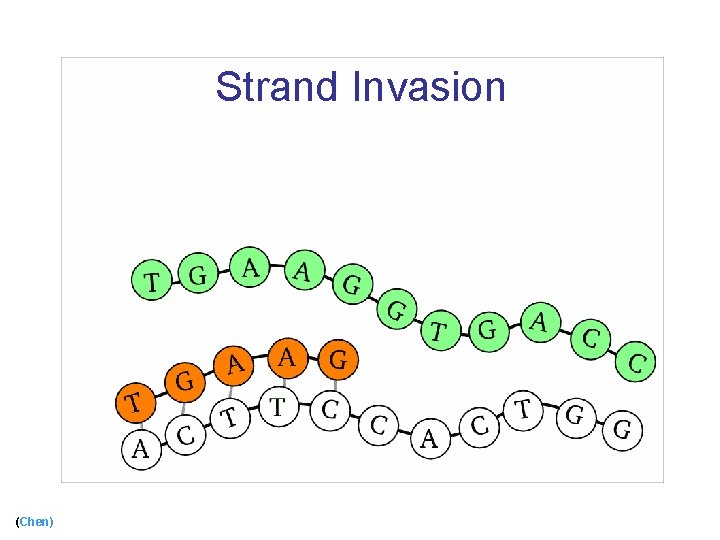
Strand Invasion (Chen)

Strand Invasion (Chen)

Strand Invasion (Chen)

Strand Invasion (Chen)

Strand Invasion (Chen)

Strand Invasion (Chen)

Strand Invasion (Chen)

Strand Invasion (Chen)

Strand Invasion (Chen)

Strand Invasion (Chen)

Strand Invasion (Chen)

Strand Invasion (Chen)

Strand Invasion (Chen)

Strand Invasion (Chen)

Strand Invasion (Chen)

Strand Invasion (cont) (Chen)

Strand Invasion (Chen)

Strand Invasion (Chen)

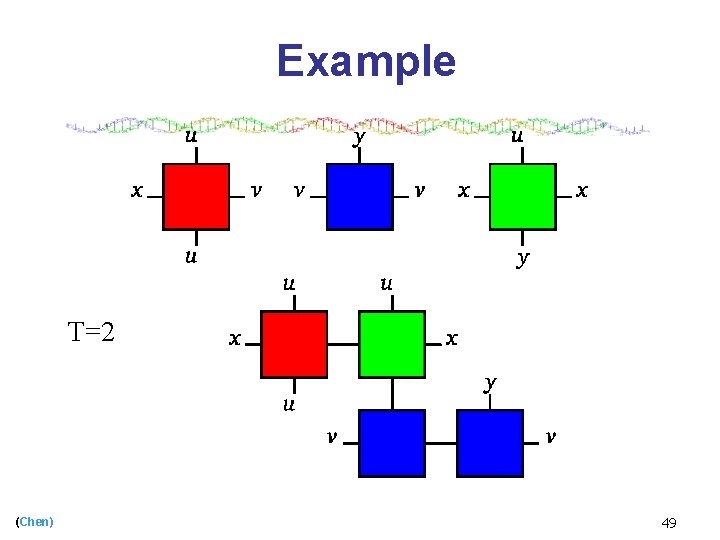
Example T=2 (Chen) 49

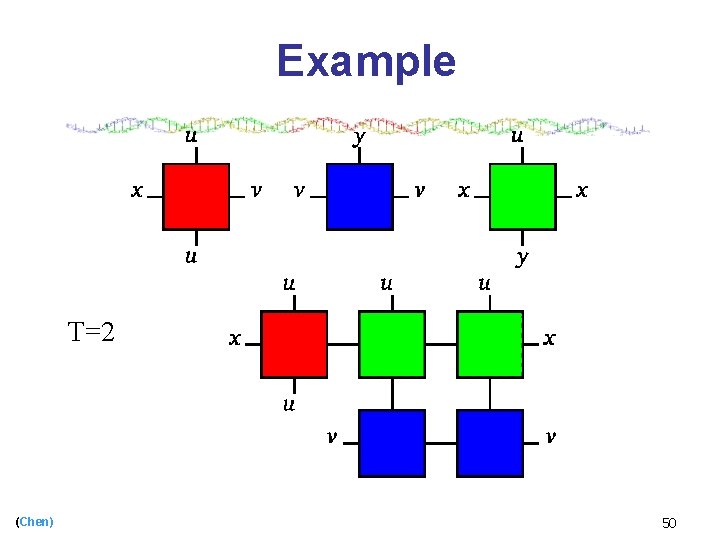
Example T=2 (Chen) 50

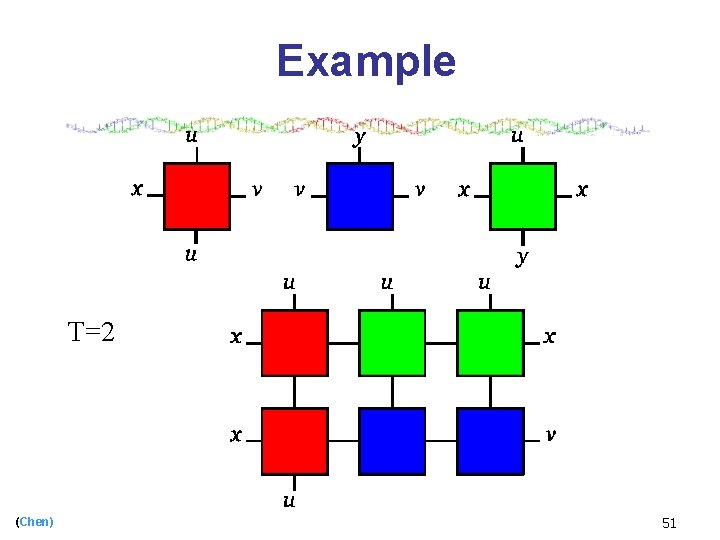
Example T=2 (Chen) 51

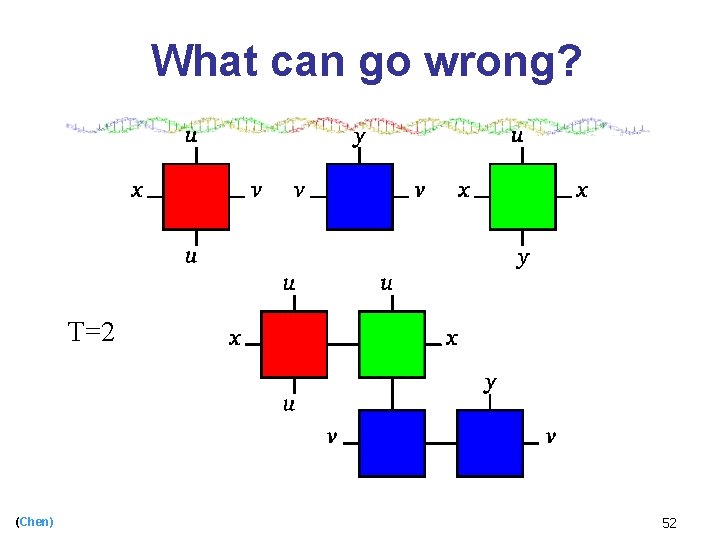
What can go wrong? T=2 (Chen) 52

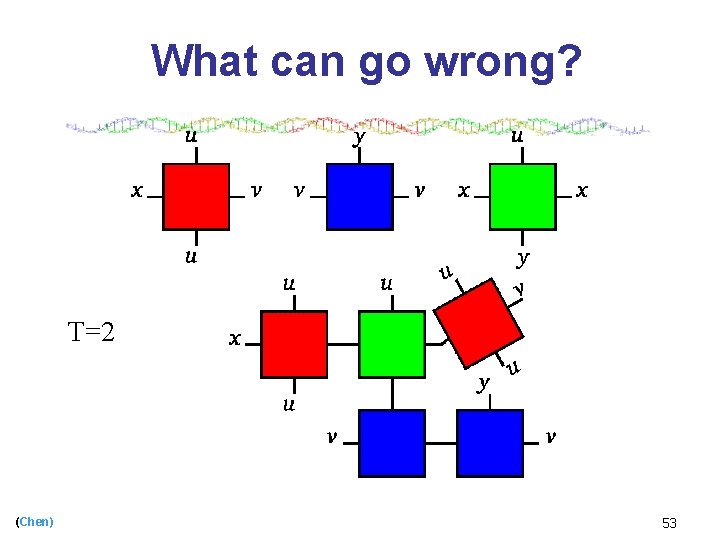
What can go wrong? T=2 (Chen) 53

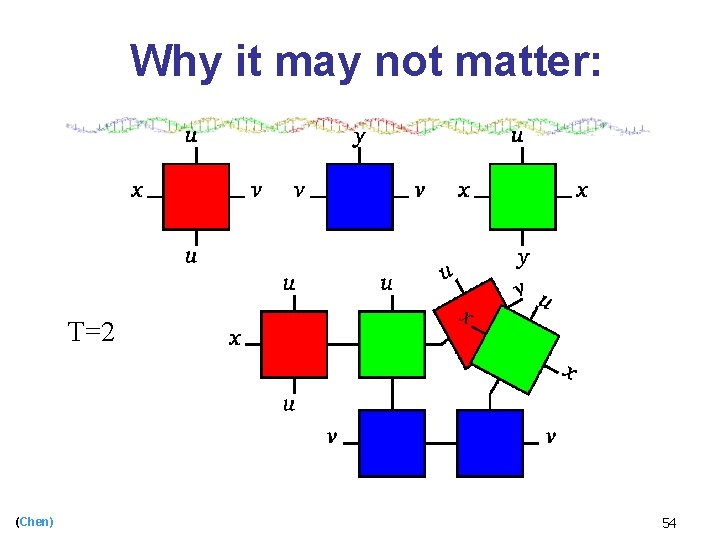
Why it may not matter: T=2 (Chen) 54

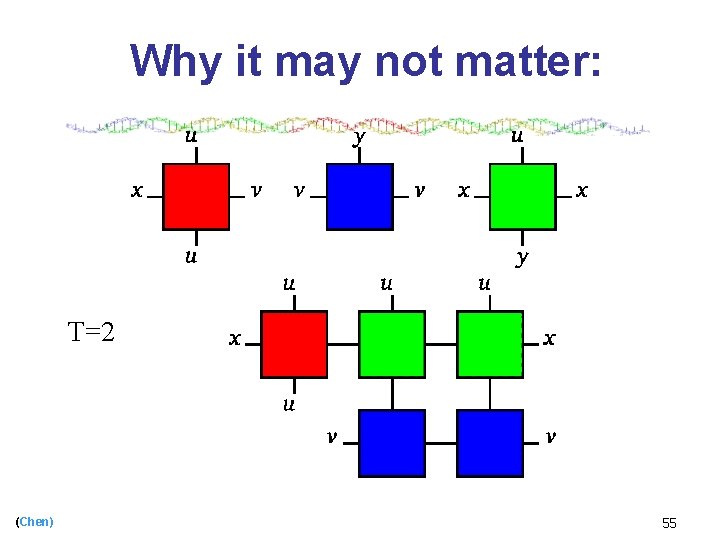
Why it may not matter: T=2 (Chen) 55

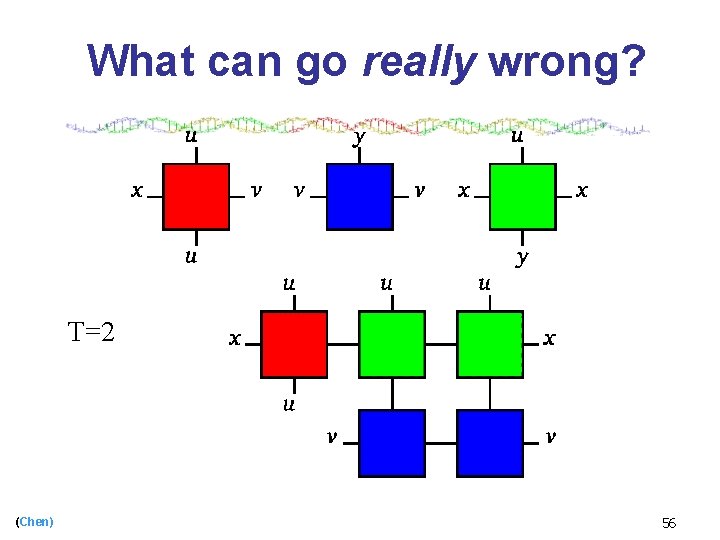
What can go really wrong? T=2 (Chen) 56

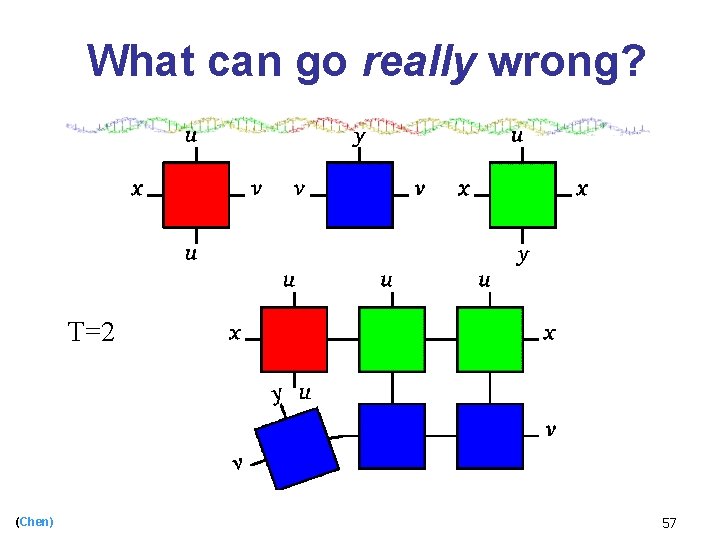
What can go really wrong? T=2 (Chen) 57

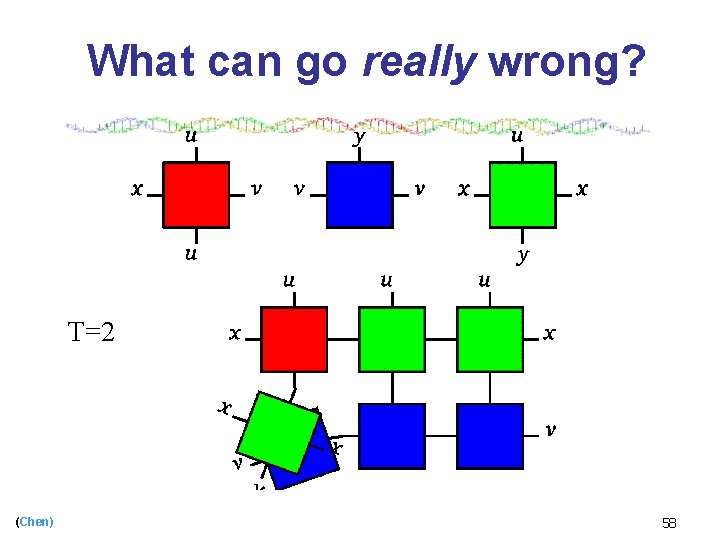
What can go really wrong? T=2 (Chen) 58

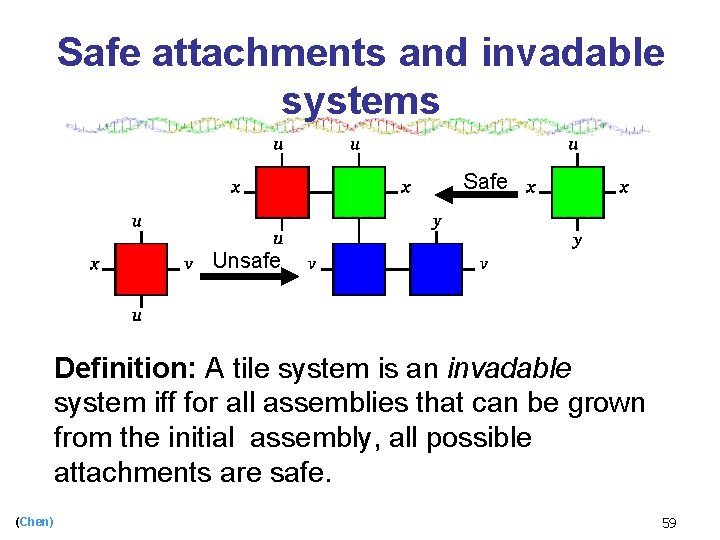
Safe attachments and invadable systems Safe Unsafe Definition: A tile system is an invadable system iff for all assemblies that can be grown from the initial assembly, all possible attachments are safe. (Chen) 59

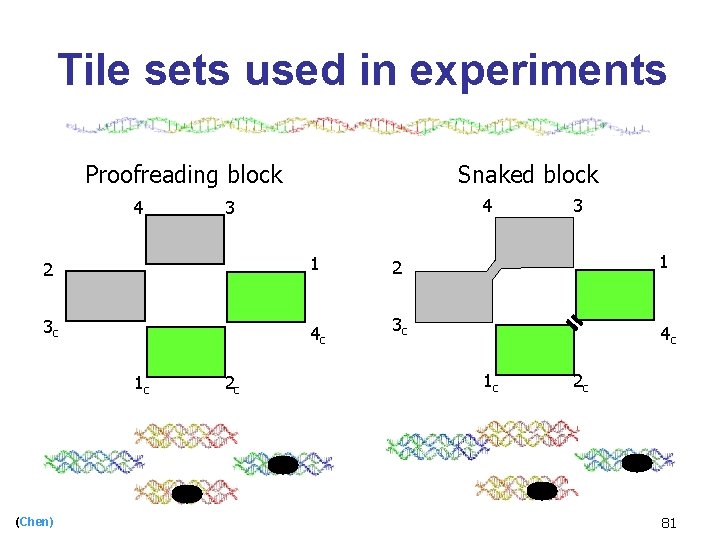
Using Combinatorial Systems n Proofreading tiles [Winfree and Bekbolatov, ’ 02] n Snaked tiles [Chen and Goel, ’ 04] n Self healing tiles [Erik Winfree, ’ 05] (Chen) 60

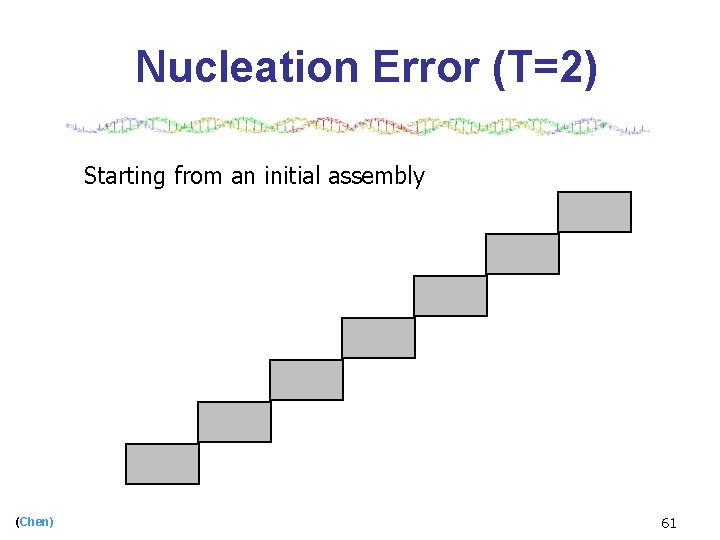
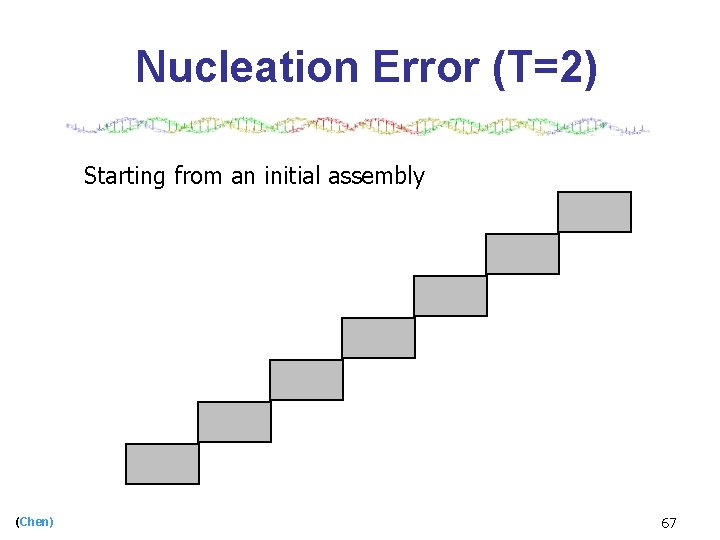
Nucleation Error (T=2) Starting from an initial assembly (Chen) 61

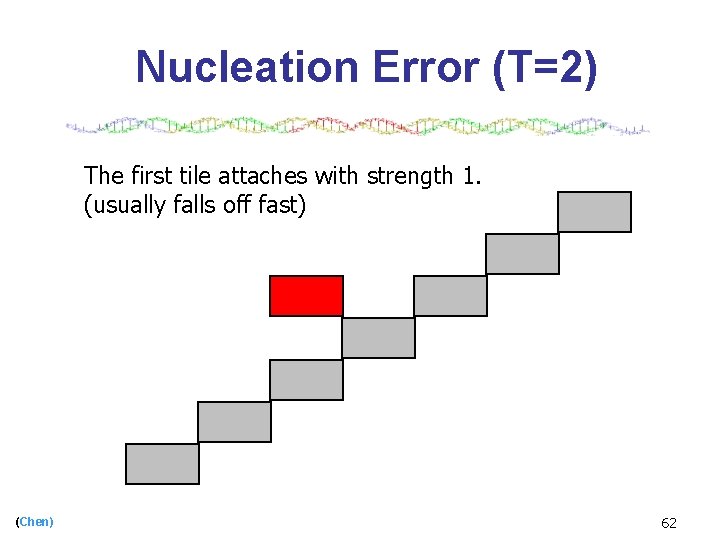
Nucleation Error (T=2) The first tile attaches with strength 1. (usually falls off fast) (Chen) 62

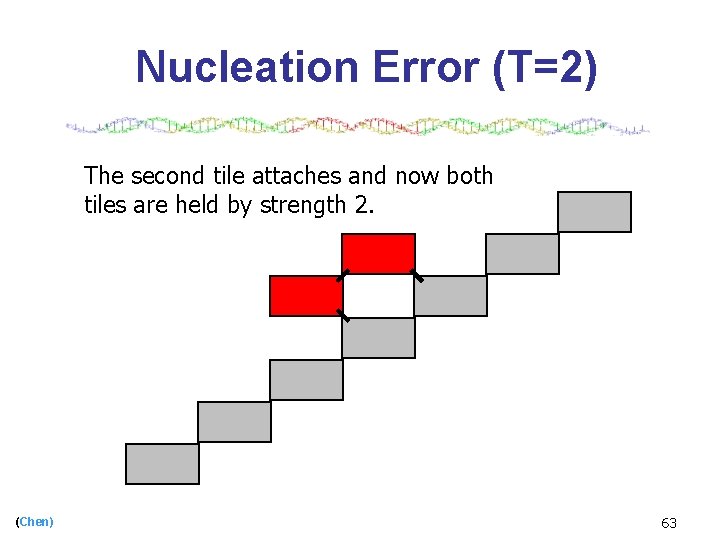
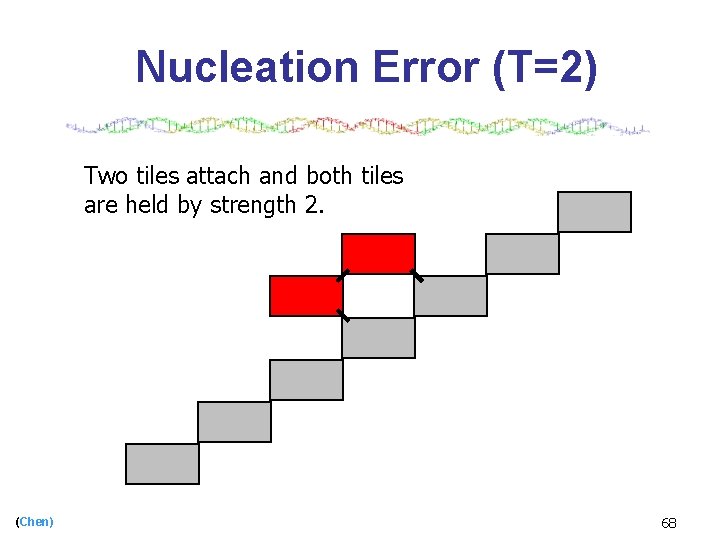
Nucleation Error (T=2) The second tile attaches and now both tiles are held by strength 2. (Chen) 63

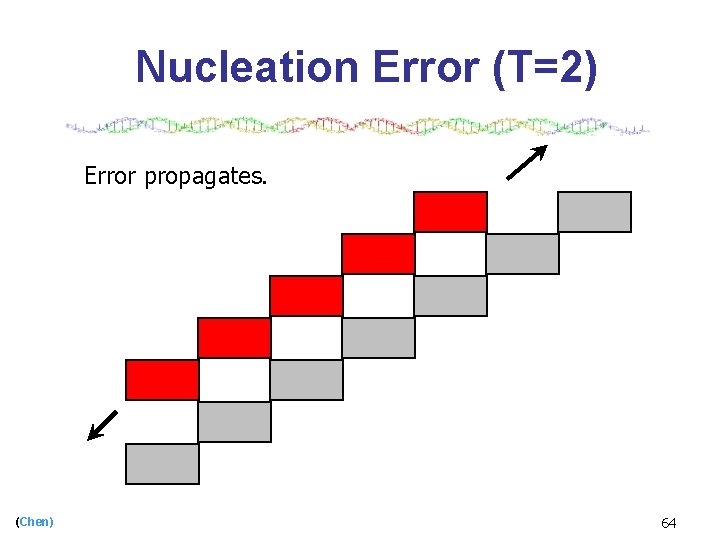
Nucleation Error (T=2) Error propagates. (Chen) 64

Modelling Errors Temperature: A positive integer. (Usually 1 or 2) A set of tile types: Each tile is an oriented rectangle with glues on its corners. Each glue has a non-negative strength (0, 1 or 2). An initial assembly (seed). Rules: A tile can attach to an assembly iff the combined strength of the “matched glues” is greater or equal than the temperature. Tiles with combined strength equal to temperature can fall off. Errors: Once a while, there will be two tiles attach at the same time and both are held by strength at least two after the attachment. We call this an “insufficient attachment”. Our goal: minimize the impact of insufficient attachments (Chen) 65

Snaked Tile System G 3 G 4 G 1 G 2 [Chen, Goel, 2004] G 3 a G 1 b • Replace a tile by a block of 4 tiles • Internal glues are unique (Chen) G 3 b G 4 b X 3 X 2 X 4 Blunt end (inert) G 1 a G 2 a G 4 a G 2 b 66

Nucleation Error (T=2) Starting from an initial assembly (Chen) 67

Nucleation Error (T=2) Two tiles attach and both tiles are held by strength 2. (Chen) 68

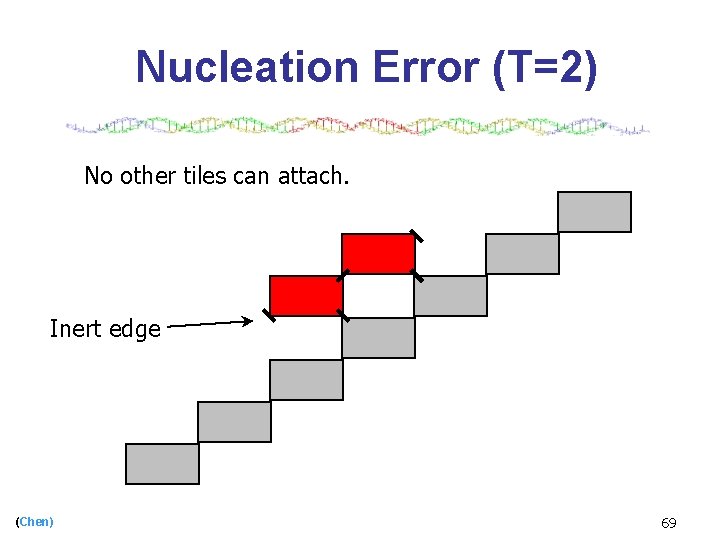
Nucleation Error (T=2) No other tiles can attach. Inert edge (Chen) 69

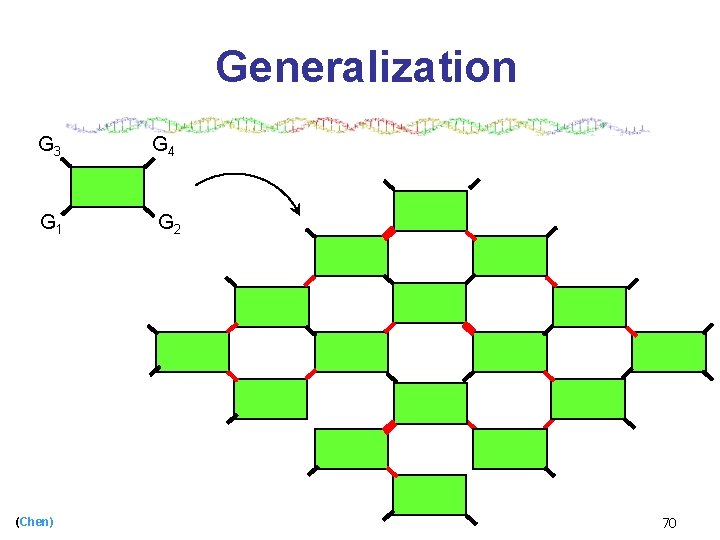
Generalization G 3 G 4 G 1 G 2 (Chen) 70

Theoretical Analysis n n (Chen) The snake tile design can be extended to 2 k by 2 k blocks. Prevents tile propagation even after k-1 insufficient attachments happen. 71

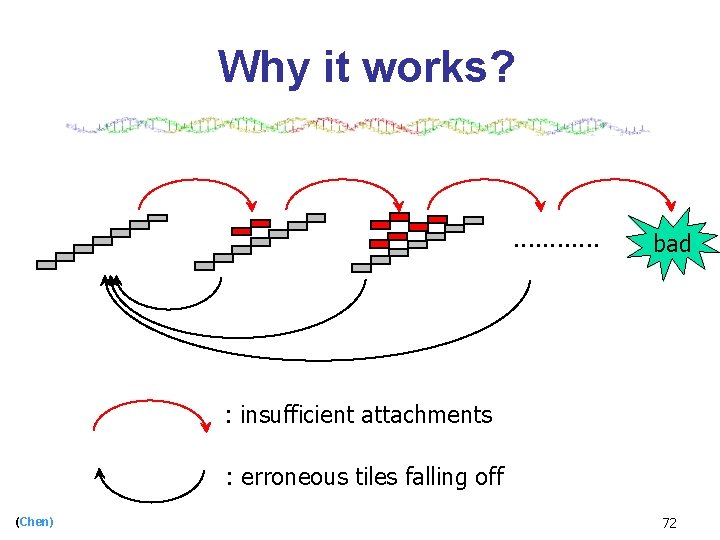
Why it works? . . . bad : insufficient attachments : erroneous tiles falling off (Chen) 72

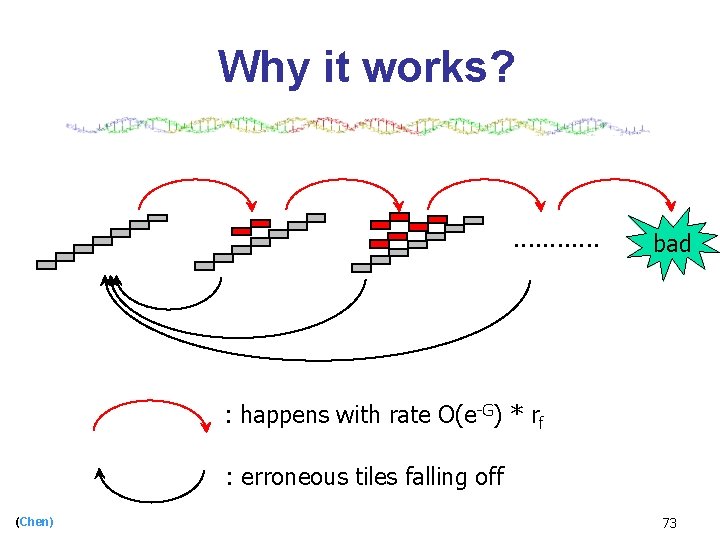
Why it works? . . . bad : happens with rate O(e-G) * rf : erroneous tiles falling off (Chen) 73

Theoretical Analysis n n n (Chen) The snake tile design can be extended to 2 k by 2 k blocks. Prevents tile propagation even after k-1 insufficient attachments happen. When < k insufficient attachments happened locally, all the erroneous tiles are expected to fall off in time poly(k). 74

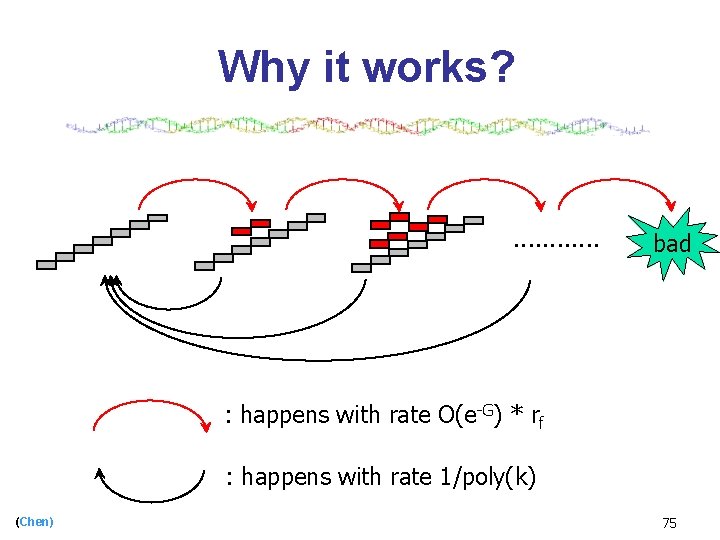
Why it works? . . . bad : happens with rate O(e-G) * rf : happens with rate 1/poly(k) (Chen) 75

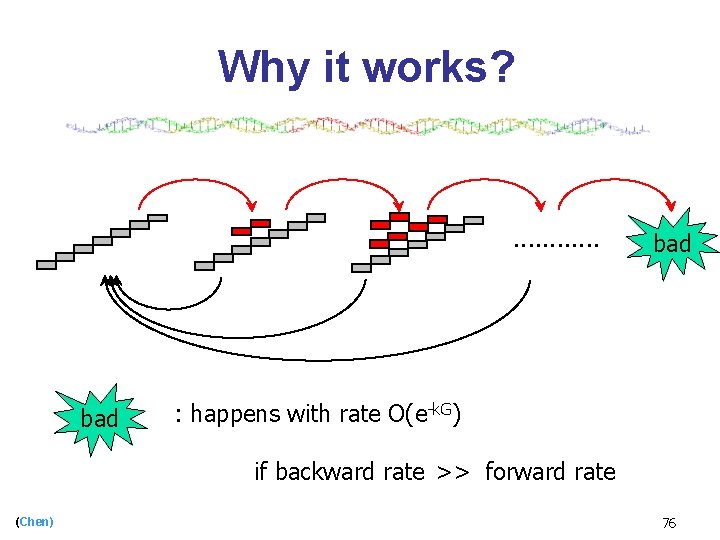
Why it works? . . . bad : happens with rate O(e-k. G) if backward rate >> forward rate (Chen) 76

Theoretical Analysis If we want to assemble a structure with size N, we can use Snaked Tile System with block size k=O(log N). (Chen) The assembly process is expected to finish within time Õ(N) and be error free with high probability. 77

Experimental Verification Joint work with Ashish Goel Rebecca Schulman Erik Winfree (Chen)

Snaked Tile System G 3 G 4 G 1 G 2 [Chen, Goel, 2004] G 3 a G 1 b • Replace a tile by a block of 4 tiles • Internal glues are unique (Chen) G 3 b G 4 b X 3 X 2 X 4 Blunt end G 1 a G 2 a G 4 a G 2 b 79

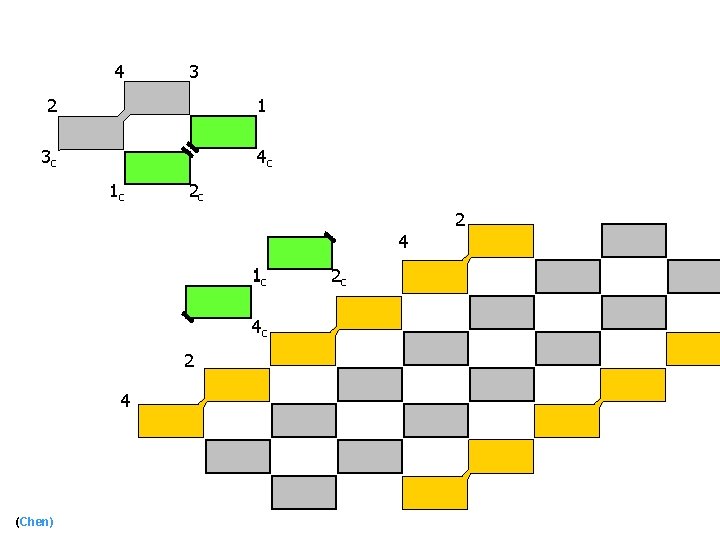
4 3 2 1 3 c 4 c 1 c 2 c 2 4 1 c 4 c 2 4 (Chen) 2 c

Tile sets used in experiments Proofreading block 4 Snaked block 4 3 3 2 1 3 c 4 c 1 c (Chen) 2 c 1 c 2 c 81

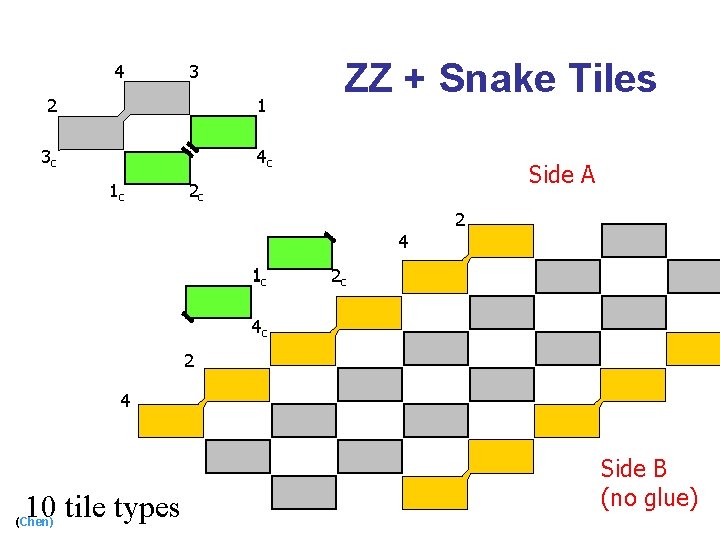
Width-4 Zig-Zag Ribbon [Schulman, Winfree, DNA 10, 2004] (Chen) 6 tile types 82

AFM of Zig-Zag Ribbons (Chen) 83

4 3 2 1 3 c 4 c 1 c ZZ + Snake Tiles Side A 2 c 2 4 1 c 2 c 4 c 2 4 10 tile types (Chen) Side B (no glue)

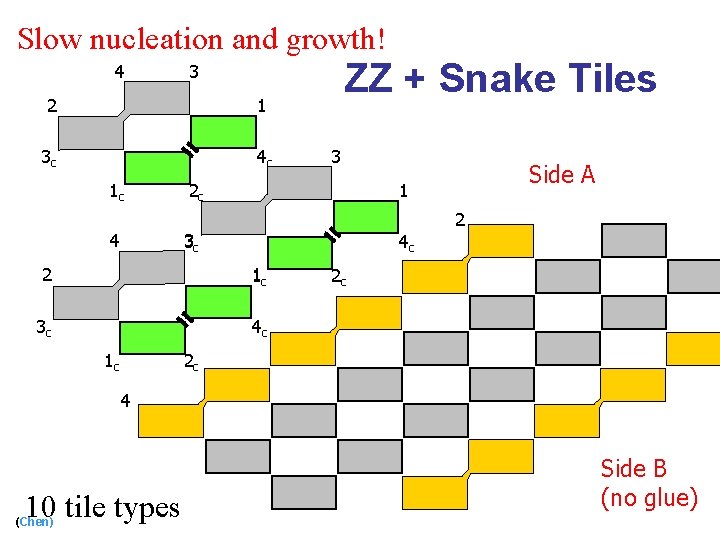
Slow nucleation and growth! 4 2 1 3 c 4 c 1 c ZZ + Snake Tiles 3 3 2 c Side A 1 2 4 3 c 4 c 2 1 c 3 c 4 c 1 c 2 c 2 c 4 10 tile types (Chen) Side B (no glue)

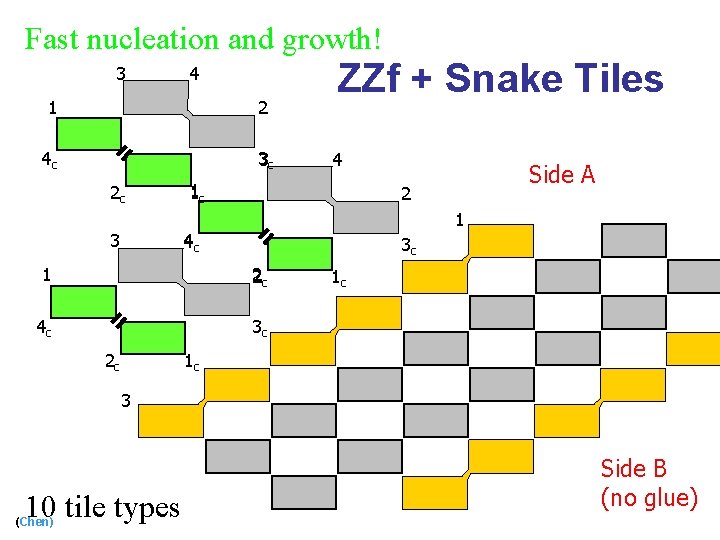
Fast nucleation and growth! 3 4 1 2 4 c 3 c 2 c ZZf + Snake Tiles 4 1 c Side A 2 1 3 4 c 3 c 1 2 c 4 c 3 c 2 c 1 c 1 c 3 10 tile types (Chen) Side B (no glue)

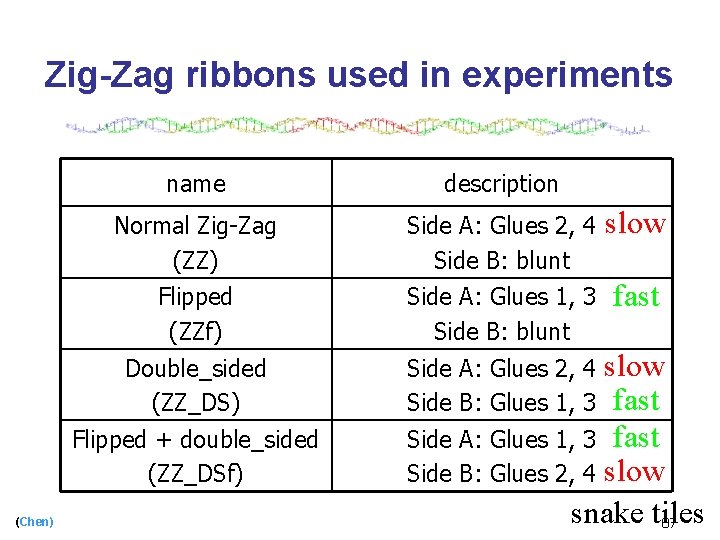
Zig-Zag ribbons used in experiments name description Normal Zig-Zag (ZZ) Side A: Glues 2, 4 Side B: blunt slow Flipped (ZZf) Side A: Glues 1, 3 Side B: blunt fast Double_sided (ZZ_DS) Side A: Glues 2, 4 Side B: Glues 1, 3 Flipped + double_sided (ZZ_DSf) (Chen) slow fast Side A: Glues 1, 3 fast Side B: Glues 2, 4 slow snake tiles 87

Experiment Results (Chen)

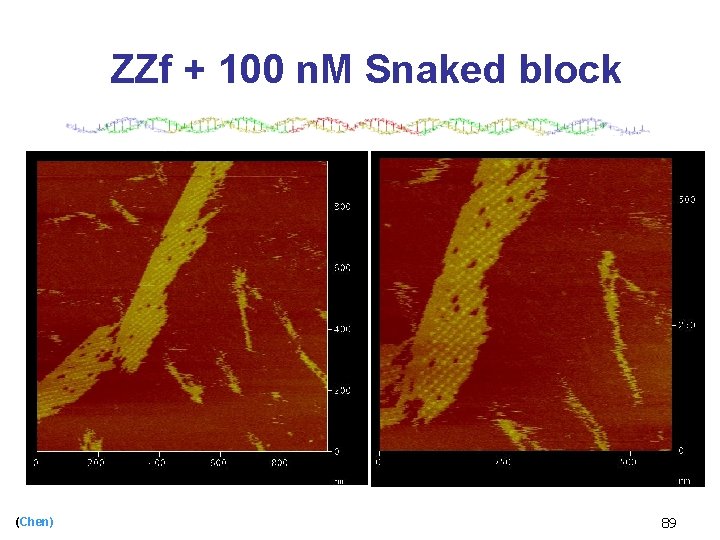
ZZf + 100 n. M Snaked block (Chen) 89

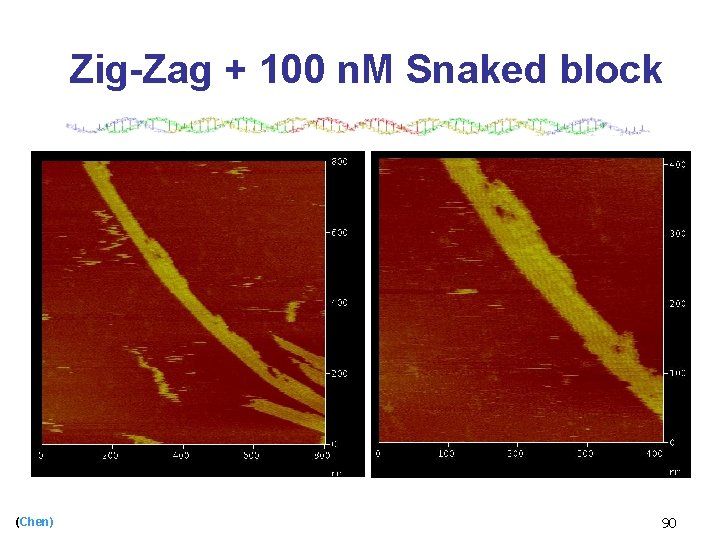
Zig-Zag + 100 n. M Snaked block (Chen) 90

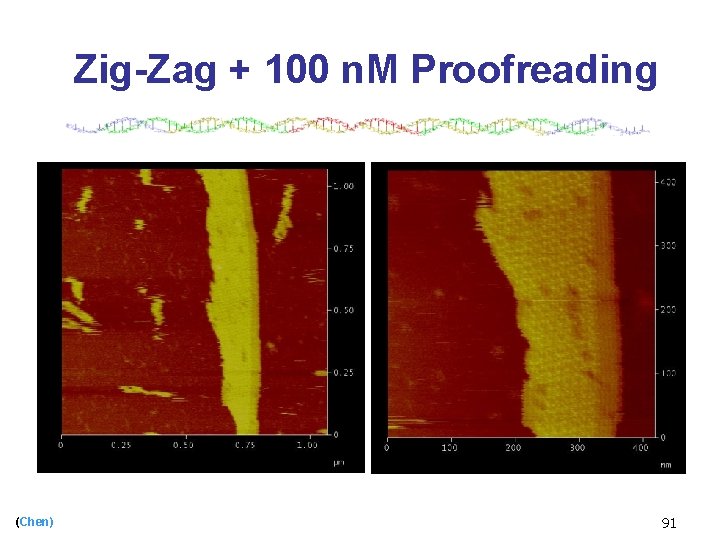
Zig-Zag + 100 n. M Proofreading (Chen) 91

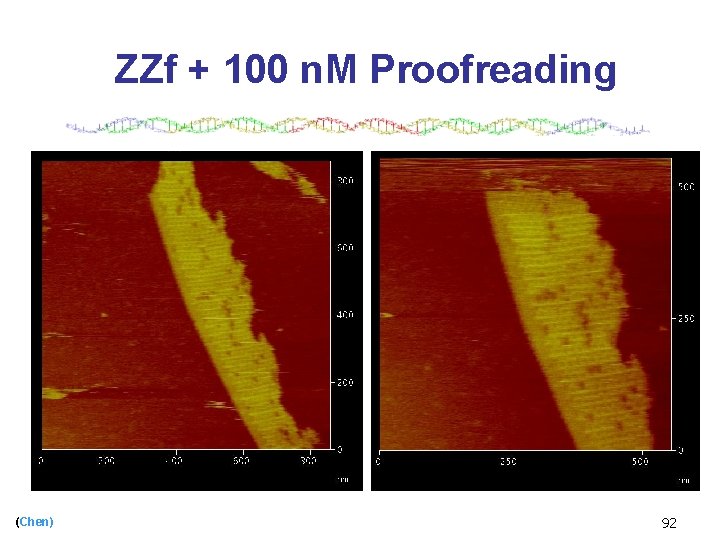
ZZf + 100 n. M Proofreading (Chen) 92

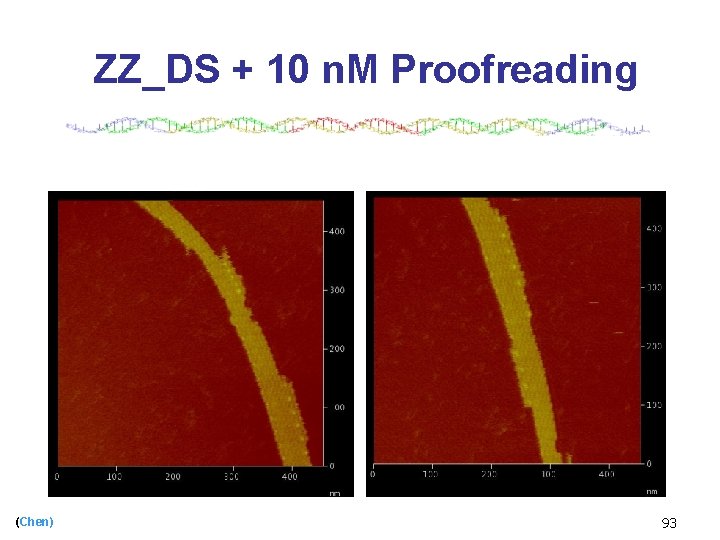
ZZ_DS + 10 n. M Proofreading (Chen) 93

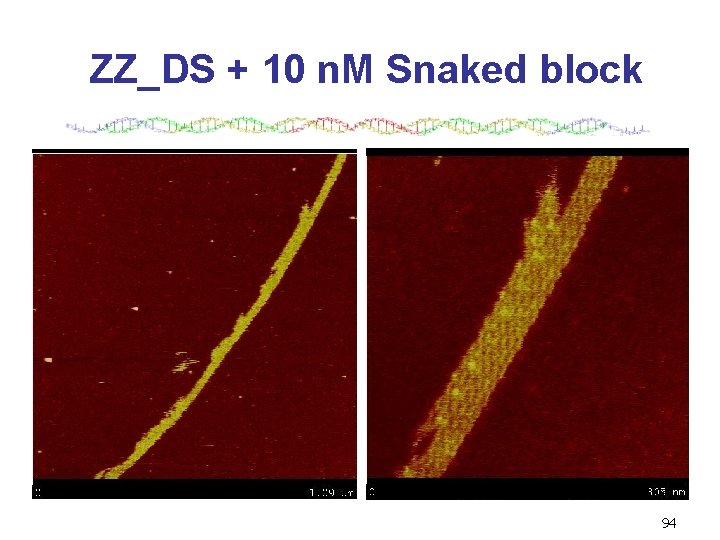
ZZ_DS + 10 n. M Snaked block 94

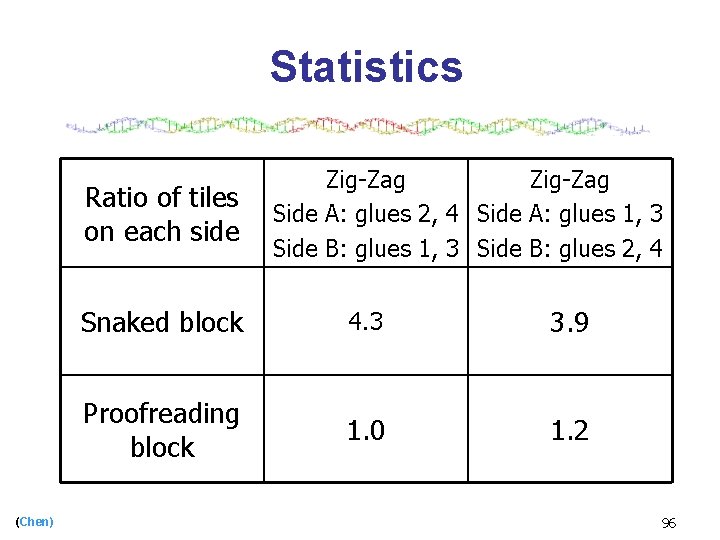
Statistics Zig-Zag Ratio of chunks Side A: glues 2, 4 Side A: glues 1, 3 on each side Side B: glues 1, 3 Side B: glues 2, 4 (Chen) Snaked block 4. 7 4. 2 Proofreading block 1. 1 1. 5 95

Statistics Ratio of tiles on each side (Chen) Zig-Zag Side A: glues 2, 4 Side A: glues 1, 3 Side B: glues 2, 4 Snaked block 4. 3 3. 9 Proofreading block 1. 0 1. 2 96

Self-healing Tile System [Winfree, ’ 05] n n n (Chen) Goal: When a big portion of the lattice is removed, it should be able to grow back correctly. Method: For each tile in the original system, we create a unique block in the new system. Idea: Use the block to prevent tile from growing backwards. 97

Assumption n n (Chen) Use abstract tile assembly model. Requires a fix set of incoming and outgoing edges for each tile in the original system. 98

Example: Sierpinski System 0 (Chen) 0 0 1 1 0 0 1 0 T=2 0 0 0 99

Example: Sierpinski System 0 0 1 1 0 0 1 0 1 1 0 0 (Chen) 0 1 T=2 0 0 1 0 0 0 100

Example: Sierpinski System (Chen) 0 0 1 1 0 0 1 0 1 T=2 101

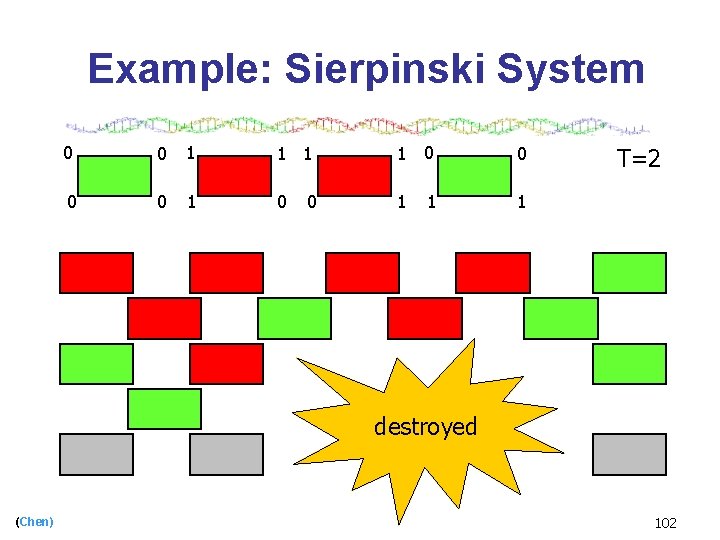
Example: Sierpinski System 0 0 1 1 0 0 1 0 1 T=2 destroyed (Chen) 102

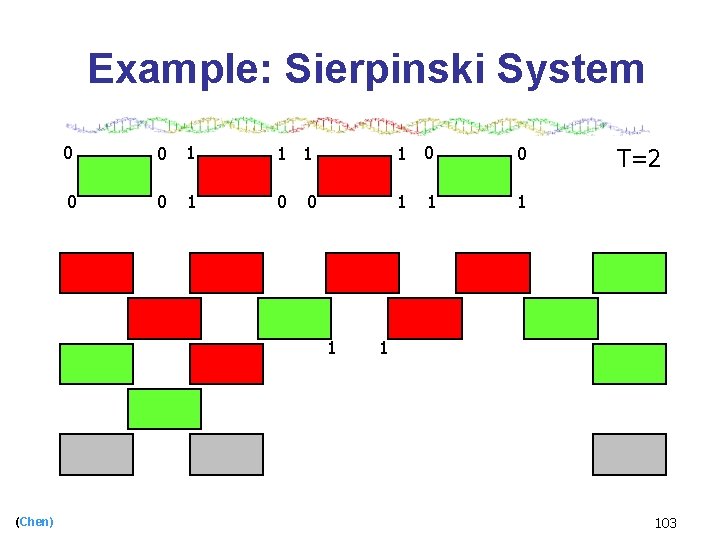
Example: Sierpinski System 0 0 1 1 0 0 1 0 1 (Chen) 1 T=2 1 103

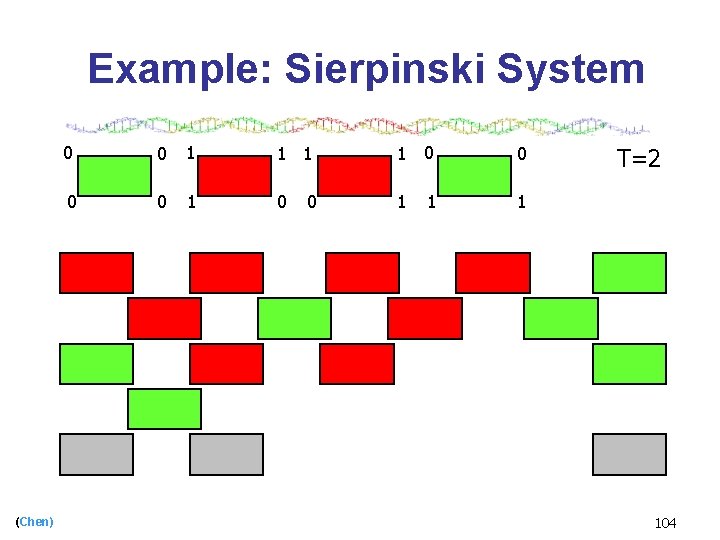
Example: Sierpinski System (Chen) 0 0 1 1 0 0 1 0 1 T=2 104

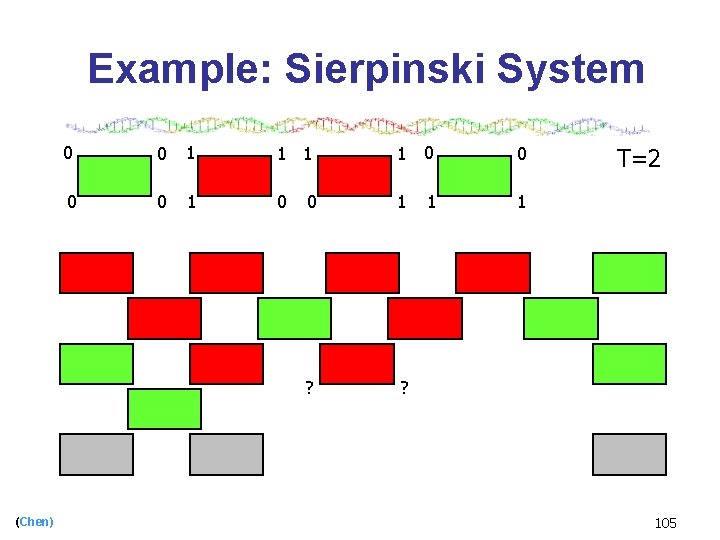
Example: Sierpinski System (Chen) 0 0 1 1 0 0 1 1 ? ? 1 T=2 105

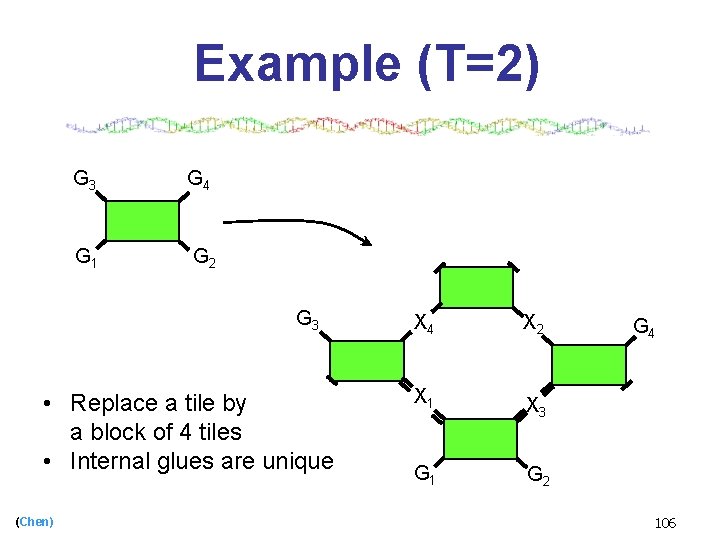
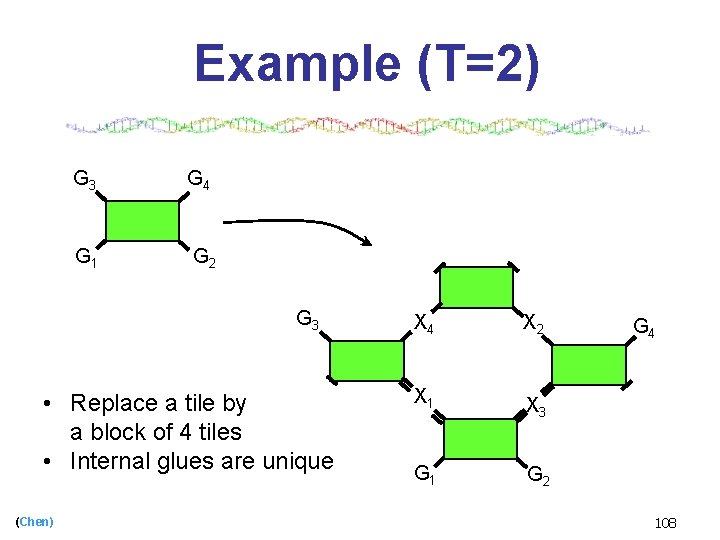
Example (T=2) G 3 G 4 G 1 G 2 G 3 • Replace a tile by a block of 4 tiles • Internal glues are unique (Chen) X 4 X 2 X 1 X 3 G 1 G 2 G 4 106

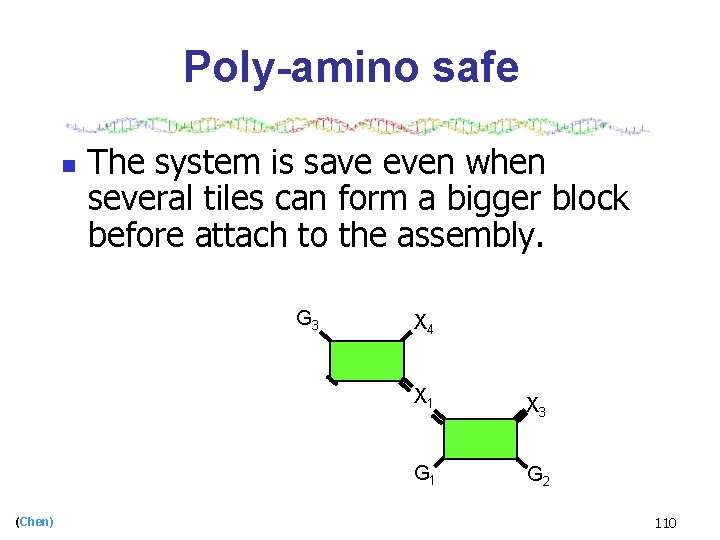
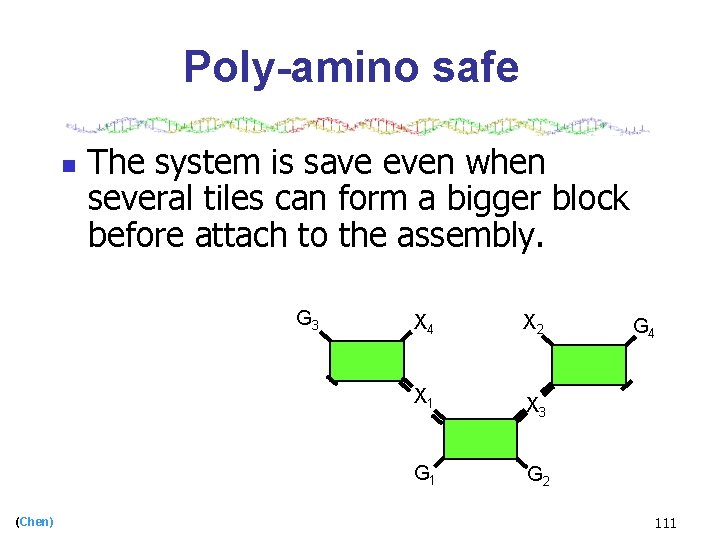
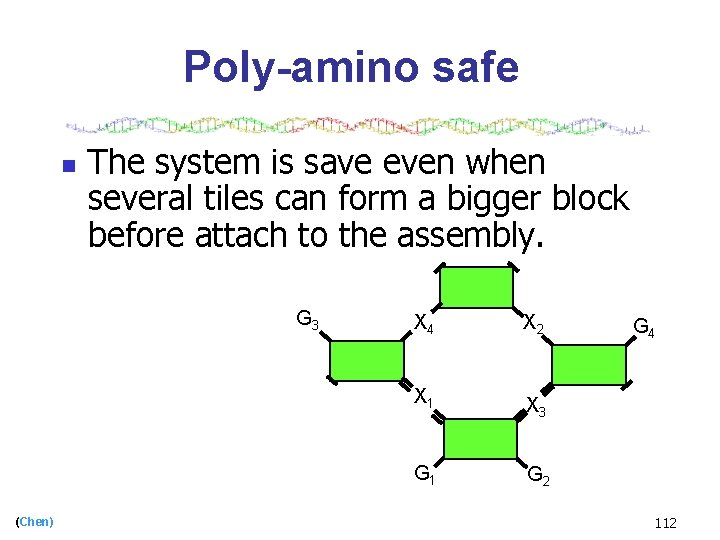
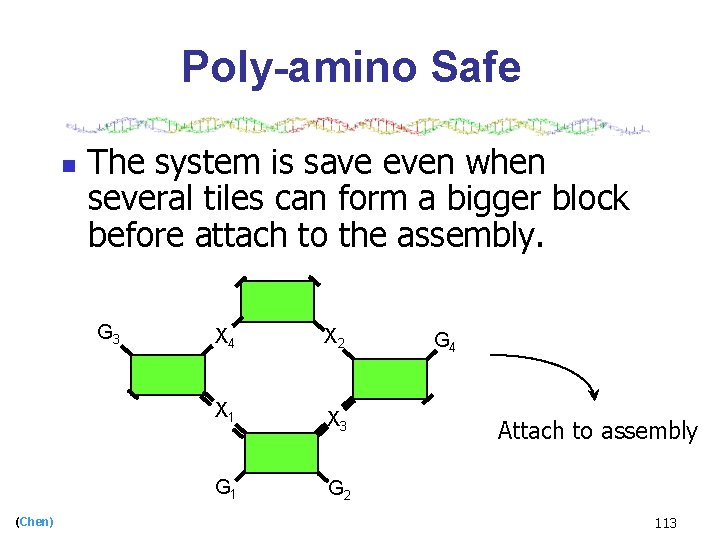
Poly-amino safe n (Chen) The system is save even when several tiles can form a bigger block before attach to the assembly. 107

Example (T=2) G 3 G 4 G 1 G 2 G 3 • Replace a tile by a block of 4 tiles • Internal glues are unique (Chen) X 4 X 2 X 1 X 3 G 1 G 2 G 4 108

Poly-amino safe n (Chen) The system is save even when several tiles can form a bigger block before attach to the assembly. X 1 X 3 G 1 G 2 109

Poly-amino safe n The system is save even when several tiles can form a bigger block before attach to the assembly. G 3 (Chen) X 4 X 1 X 3 G 1 G 2 110

Poly-amino safe n The system is save even when several tiles can form a bigger block before attach to the assembly. G 3 (Chen) X 4 X 2 X 1 X 3 G 1 G 2 G 4 111

Poly-amino safe n The system is save even when several tiles can form a bigger block before attach to the assembly. G 3 (Chen) X 4 X 2 X 1 X 3 G 1 G 2 G 4 112

Poly-amino Safe n The system is save even when several tiles can form a bigger block before attach to the assembly. G 3 (Chen) X 4 X 2 X 1 X 3 G 1 G 2 G 4 Attach to assembly 113

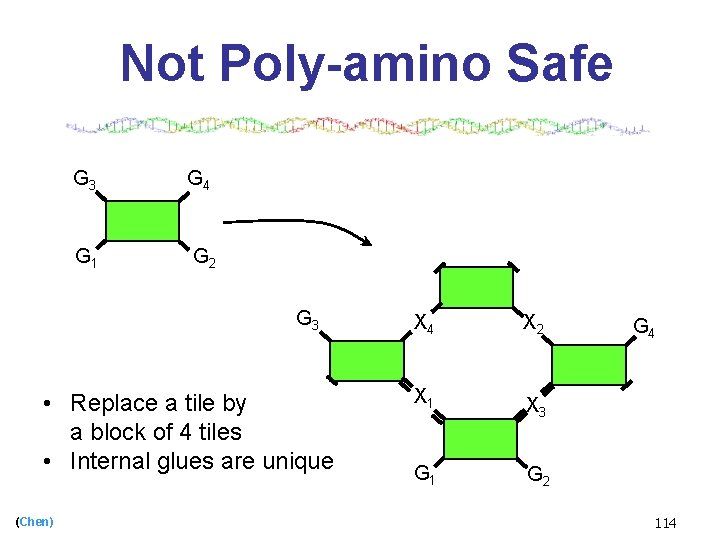
Not Poly-amino Safe G 3 G 4 G 1 G 2 G 3 • Replace a tile by a block of 4 tiles • Internal glues are unique (Chen) X 4 X 2 X 1 X 3 G 1 G 2 G 4 114