Do Now Error Uncertainty Propagation Reporting Absolute Error

Do Now

Error & Uncertainty Propagation & Reporting Absolute Error or Uncertainty is the total uncertainty in a measurement reported as a ± with the measurement.

Three styles for expressing uncertainties: Absolute uncertainty. V ± ΔV = (13. 8 ± 0. 2) m. L V falls within 13. 6 – 14. 0 m. L Fractional or Relative ΔV / V = 0. 2 / 13. 8 ≈ 0. 0145 Compares Abs. to actual measure. Percentage ΔV % = (ΔV / V) × 100 = (0. 2 / 13. 8) × 100 ≈ 1. 4 %

Absolute Uncertainty show a range 4. 5 kg 0. 1 kg Absolute Uncertainty or Error This says the actual value lies between 4. 4 – 4. 6 kg. The absolute error should be 1 SF only. Its place must agree with the measurement’s place. ST called raw unc.

Where absolute error come from? How do you know the correct range? • Measure the diameter of a ball with the ruler. Report your measurement.

• At minimum it’s the instrument uncertainty. • Usu instrument uncertainty plus other uncertainty sources. Use your judgment but be logical. • Ball radius in drop height. • Meniscus in graduated cylinder.

Instrument Uncertainty • For scales where you can read between 2 divisions, you can report ½ the smallest or the actual smallest measure as your instrument uncertainty (I generally use the smallest increment). • For digital measures just report the smallest unit.

Absolute Uncertainty of Mean • Unc. Shrinks w more trials. • Generally experiment requires a 5 x 5 table. Five trials, Five different values for independent variable. • Take five different drop heights, 5 trials each. Measure the time to hit the ground. Average times. • For set of measurements, absolute uncert: (Max – Min) / 2

1: Given Ball drop experiment with set of drop times in seconds for 1 height: • • • 0. 23 0. 22 0. 26 0. 34 0. 18 • Find the mean and the absolute uncertainty of the mean. • Proper value = • mean = 0. 246 s • unc. is • (0. 34 – 0. 18)/2 • 0. 08 • 0. 25 ± 0. 08 s

Ways of reporting uncertainty • • Absolute uncertainty is a range. Fractional / Relative uncertainty % uncertainty/error % difference/discrepancy

Relative/fractional Uncertainty or Error gives idea of what fraction of the measure the uncertainty represents. It is calculated as: Absolute Uncertainty Measurement 2. For the measure 4. 5 kg relative and % uncertainty 0. 1 kg find 0. 022 or 2. 2% Relative Error/Uncert. This does not get a ±. It can be more than 1 SF.

% Uncertainty/Error is different than % difference, deviation, discrepancy. % Dif measures difference from accepted value: Accept val – meas val x 100% Accepted Val % Error - amount of uncertainty in measurement.

Propagation of Error • Measure height of counter in cm with a meter-stick. • Measure height of student with meter-stick. • Which has more uncertainty? • If you do calculations with the measurements with uncertainties – the uncertainty will increase.

Adding or subtracting measurements, the total absolute error is the sum of the absolute errors! Data booklet reference: • If y = a b then y = a + b 2. 61 0. 05 cm 5. 6 0. 1 cm + 2. 82 0. 05 cm - 2. 1 0. 1 cm 5. 4 0. 1 cm Decimal Agreement 3. 5 0. 2 cm

Multiplication & Division • 1 st – solve it! Find product or quotient normal way. • Must calculate relative or percent uncertainty for each individual measure. • Then add the relative/percent errors. • If y = a · b / c then y / y = a / a + b / b + c / c • Absolute Error is reported as fraction of the answer.

• 3. Find the area of a rectangle measuring: 2. 6 cm ± 0. 5 by 2. 8 ± 0. 5 cm? Solve A = l x w: 7. 28 cm 2.

Find the relative/percent error of each measurement: 0. 5 ÷ 2. 6 = 0. 192 0. 5 ÷ 2. 8 = 0. 179 Sum the relative errors: 0. 192 + 0. 179 = 0. 371 or 37% If y = a · b / c then y / y = a / a + b / b + c / c Abs Unc. multiply relative unc. by the answer. 0. 371 x 7. 28 cm 2 = 2. 70 cm 2. This is the ± giving the range on your measurement. It means 7. 28 ± 2. 70 cm 2.

Round uncertainty (not meas) 1 SF &report 2. 70 cm 2 becomes ± 3 cm 2. Answer gets rounded to the same place as ±. 7. 28 cm 2 = becomes 7 cm 2 to agree with 3 cm 2. Report: 7 cm 2 ± 3 cm 2.

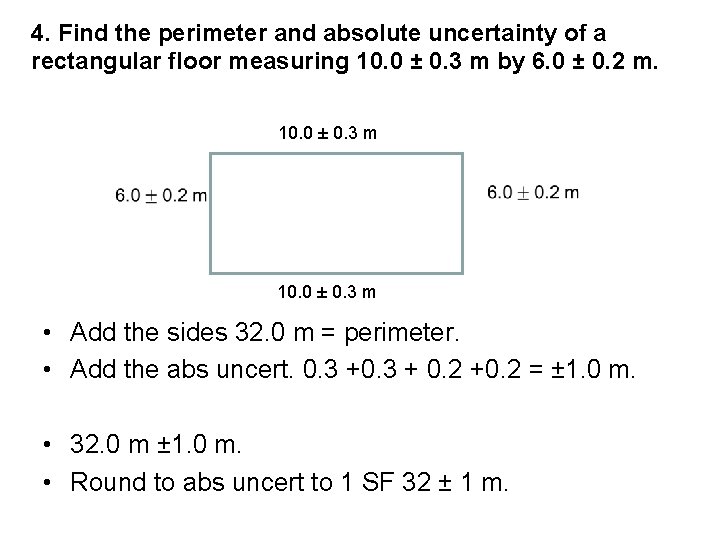
4. Find the perimeter and absolute uncertainty of a rectangular floor measuring 10. 0 ± 0. 3 m by 6. 0 ± 0. 2 m. 10. 0 ± 0. 3 m • Add the sides 32. 0 m = perimeter. • Add the abs uncert. 0. 3 + 0. 2 +0. 2 = ± 1. 0 m. • 32. 0 m ± 1. 0 m. • Round to abs uncert to 1 SF 32 ± 1 m.

Raising measurements to power n • Solve equation • Find relative uncertainty. • Multiply relative uncertainty by n (power). • • If y = a n then y / y = | n · a / a |

5: find volume of cube with side length of 2. 5 0. 1 cm. • Volume = (2. 5 cm)3 = 15. 625 cm 3. • Relative uncertainty for each side = 0. 1 cm 2. 5 cm = 0. 04

0. 04 x 3 (nth power) = 0. 12 This is the fraction of uncertainty in the volume measure. 0. 12 (15. 625 cm 3. ) = 1. 875 cm 3. Round to uncertainty to 1 sig fig ± 2 cm 3.

Finish • Round last digit of answer to same place as abs uncertainty. Uncertainty to 1 SF was 2 cm 3 (one’s place). • Ans was 15. 625 cm 3. • So 16 cm 3 ± 2 cm 3.

6. A protractor is precise to ± 1 o. A student obtains the following measurements for a refraction angle: 45, 47, 46, 45, and 44 degrees. How show he express the refractive angle with its uncertainty? • • • Mean = 45. 4 o. Max – Min = 47 – 44 = 3 o. Half range = 1. 5 o. With rounding: Value = 45 ± 2 o.

Uncertainty Tutorial https: //www. youtube. com/watch ? v=0 lt-9 qim. Lf 4

Exact/ pure numbers There are no uncertainties associated with pure numbers, the type of operation determines the uncertainty propagation where, for example: If a quantity is divided by 2, the uncertainty in the 2 is zero. If you multiply a quantity by π, the uncertainty in π is zero. The only uncertainty in πr 2 is in the measurement of r, where r is ± Δr. For multiplication by an exact number, multiply the uncertainty by the same exact number. For division, divide uncert by number.

Uncertainty in Series of Measurements Take the average value and determine the uncertainty from the range. The range is the difference between the largest and smallest measurements. The uncertainty is ± one half the range. Given 4 measurements: • x 1 = 32, x 2 = 36, x 3 = 33, x 4 = 37 • mean of x = (x 1 + x 2 + x 3 + x 4) / 4 = 35. 5 (Average) • Abs uncert , Δx = ±(xmax – xmin) / 2 = (37 – 32) / 2 = 2. 5 • mean of x ± Δx = 35. 5 ± 2. 5 ≈ 36 ± 3.

Reciprocals, logarithms, & trigonometric functions. Uncertainties are not usually symmetrical. Make minimum and maximum calculations for the uncertainty range then round to a positive or negative symmetrical value. θ ± Δθ = (13 ± 1)° sin 13° = 0. 22495 sin 14° = 0. 24192 sin 12° = 0. 20791 sin(13 ± 1)° = 0. 22495 (+0. 01704 and – 0. 01697) sin(13 ± 1)° = 0. 22 ± 0. 02