Hypothesis Testing A hypothesis is a conjecture about

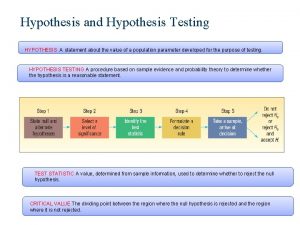
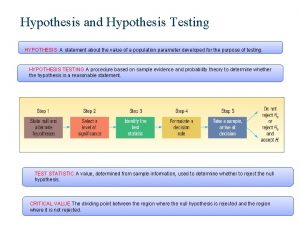
Hypothesis Testing A hypothesis is a conjecture about a population. Typically, these hypotheses will be stated in terms of a parameter such as m (mean) or p (proportion). A test of hypothesis is a statistical procedure used to make a decision about the conjectured value of a parameter. We will make our decision based on observed values of a test statistic and resulting p-value.

The Hypotheses There are two hypotheses which we are comparing. The null hypothesis, H 0, specifies a value of a parameter. This hypothesis is assumed to be true, and an experiment is conducted to determine if the collected data is contradictory to the null hypothesis. The alternative (or research) hypothesis, Ha, gives an opposing statement about the value of the parameter. The collected data will be analyzed to see if it supports the alternative hypothesis.

Statistical Terminology Once the data is collected, we seek an answer to the question: “If the null hypothesis is true, how likely are we to observe this type of data, or data which is more extreme in the direction of the alternative hypothesis? ” The observed significance level, or p-value of a test of hypothesis is the probability of obtaining the observed value of the sample statistic, or one which is even more supportive of the alternative hypothesis, under the assumption that the null hypothesis is true.

Empirical Rule Example One thing you might think of initially is to see if the value (or statistic’s value) is where you expect it to be. If H 0 says the population mean should be 78 bpm (heart rate) with a standard error of the mean of 3 bpm, then you know from the empirical rule that roughly 95% of heart rates should lie between 72 bpm and 84 bpm. So if a sample mean of patients on a new drug, for example, have a rate of 73 bpm, that is expected. If the sample mean is 86 bpm, that might be cause for concern.

Test Statistics and P-values Obviously, we must be able to calculate these p-values. A test statistic is a quantity calculated from the sampled value of a statistic, which is then used to calculate a p-value for a test of hypothesis. We recall that under appropriate conditions, we know the sampling distribution of the sample mean follows a normal distribution, and we can find a t-score using

Using P-values to make Decisions We must decide when to accept that the research hypothesis has been proven beyond some reasonable doubt. This is called a significance level, and is denoted by a. When the probability of the sample data is below this level of significance, we conclude there is enough evidence to assert the research hypothesis is true. So we accept Ha when the p-value is less than or equal to the level of significance. (decision rule)

Steps of the t-Test of Hypothesis for m 1. Identify the null and alternative hypotheses 2. Give the decision rule 3. Identify the form of the test statistic and calculate it based on the sampled data 4. Verify the method is valid (random sample, s is unknown, and n is at least 30 or population is known to be normally distributed ) 5. Calculate the p-value based on the t-score and Ha 6. Give an interpretation. (sentence)

Hypothesis Testing Example A local radio station claims that they play an average of 54 minutes every hour. A listener believes this statement is incorrect, and wants to prove that this station plays less than 54 minutes of music, on average, each hour. The listener monitors 36 different 1 -hour time slots and records the amount of time during that hour which the station played music. She finds that the mean and standard deviation for the 36 observations are 53. 2 minutes and 2. 1 minutes, respectively. Does this provide evidence that the listener is correct? Test using a. 05 level of significance.

Hypothesis Testing Example 1. H 0: m = 54 minutes Ha: m < 54 minutes 2. Decision Rule: Accept Ha if the p-value <. 05. 3. = – 2. 3 4. Valid since a random sample was taken, s is unknown so we use s = 2. 1 min, and n = 36 is “at least 30”.

Hypothesis Testing Example 5. p-value =. 0138 df = n – 1 = 36 – 1 = 35, We will obtain the p-value from software using the actual sample data set. 6. At the. 05 level of significance, there is sufficient evidence to conclude the mean time per hour this station plays music is less than 54 minutes.

Hypothesis Testing Example Historically, the mean time until a patient feels relief from pain after surgery on the standard medication has been 3 minutes. A new drug is available which researchers hope will lead to faster average relief times for patients after surgery. A random sample of 41 patients were given this new medication after surgery and the time until the patient felt relief was recorded. What is the research hypothesis?

Hypothesis Testing Example A new drug is available which researchers hope will lead to faster average relief times for patients after surgery. What is the research hypothesis? So Ha: m < 3 minutes where m is the mean relief time among all patients who take this new drug after surgery. Also, this implies H 0: m > 3 minutes.

Hypothesis Testing Example Suppose the mean relief time was 2. 8 minutes and the standard deviation was 0. 92 minutes for the 41 patients. Does this allow the researchers to conclude the new drug is faster, on average? Use a = 0. 05. Decision rule: Accept Ha if the p-value < 0. 05. Test Statistic: t = -1. 39 (see next slide for output) P-value: 0. 086 At the. 05 level of significance, there is not enough evidence to conclude the new drug is faster, on average.

Hypothesis Testing Example Stat. Crunch Output for the Entire Test: Hypothesis test results: μ : population mean H 0 : μ = 3 HA : μ < 3

Possible Errors Realize, that a small p-value (or observed level of significance) suggests that the alternative hypothesis is true, but does not guarantee it is true. A Type I Error consists of concluding that the alternative hypothesis is true when, in fact, the null hypothesis is true. A Type II Error consists of concluding that the null hypothesis is true when, in fact, the alternative hypothesis is true.

Type I or Type II Errors We can examine each error and attempt to control how willing we are to commit each. The probability of committing a Type I Error is given by a(alpha), the level of significance of the test. The probability of committing a Type II Error is given by b (beta). We will decide the seriousness of each error, and then determine relative values for a and b.

Type I or Type II Errors H 0: Dental lab is not contaminated with mercury vapor. Ha: Dental lab is contaminated with mercury vapor. A Type I Error occurs if we conclude the lab is contaminated when, in fact, the lab is not contaminated with mercury vapor. Consequences: The office would probably be closed, and procedures to reduce the mercury vapor levels would be implemented. This means costs for decontamination and lack of income from patients, but no one is endangered.

Type I or Type II Errors H 0: Lab is not contaminated with mercury vapor. Ha: Lab is contaminated with mercury vapor. A Type II Error occurs if we conclude the lab is NOT contaminated when, in fact, the lab is contaminated with mercury vapor. Consequences: The office would be open and new patients and workers could be exposed to high levels of mercury vapor. This means possible law suits, people getting sick, dangerous work environment. It could lead to a bad reputation for this dental office.

Type I or Type II Errors H 0: Lab is not contaminated with mercury vapor. Ha: Lab is contaminated with mercury vapor. Which error is worse? Probably Type II in my opinion. Hence, I want to avoid this, so I set the probability low. The Type I Error means a loss of income, so it’s not good for business, but it’s not as serious. I’d set a more than b.

Type I or Type II Errors Be able to define a Type I Error and a Type II error in terms of a scenario. Be able to discuss the consequences of each type of error. Set relative values for a and b depending on those consequences (which is larger and which is smaller, or are both about equal? ). There are no rules on one error being worse than the other in all situations.