CHAPTER 4 RoundOff and Truncation Errors Numerical Accuracy

CHAPTER 4 Round-Off and Truncation Errors

Numerical Accuracy Truncation error : Method dependent § Errors which result from using an approximation rather than an exact procedure Round-off error : Machine dependent § Errors which result from not being able to adequately represent the true value § Result from using an approximate number to represent exact number

Taylor Series Expansion § Construction of finite-difference formula § Numerical accuracy: discretization error a x Base point x = a

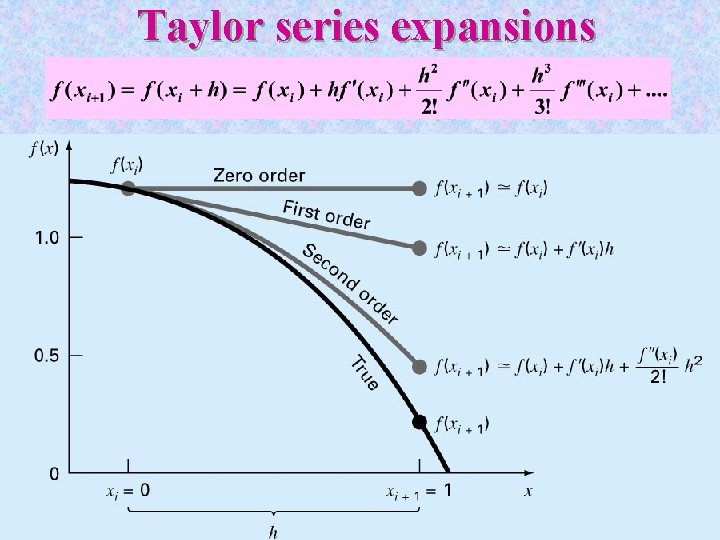
Taylor series expansions

Taylor Series and Remainder § Taylor series (base point x = a) § Remainder

Truncation Error § Taylor series expansion § Example (higher-order terms truncated) (xi = 0, h = x xi+1 = x)

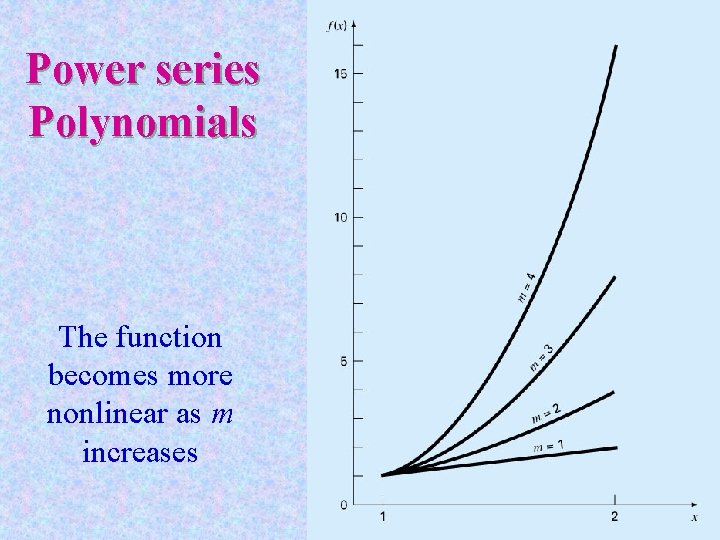
Power series Polynomials The function becomes more nonlinear as m increases

A MATLAB Script § Filename: fun_exp. m function sum = exp(x) % Evaluate exponential function exp(x) % by Taylor series expansion % f(x)=1 + x^2/2! + x^3/3! + … + x^n/n! clear all x = input(‘enter the value of x = ’); n = input(‘enter the order n = ’); term =1 ; sum= term; for i = 1 : n term = term*x/i; sum = sum + term; end

MATLAB For Loops § Filename: fun_exp 2. m function sum = exp(x) % Evaluate exponential function exp(x) % by Taylor series expansion % f(x)=1 + x^2/2! + x^3/3! + … + x^n/n! x = input(‘enter the value of x =’); n = input(‘enter the order n = ’); term(1) =1 ; sum(1)= term(1); for i = 1 : n term(i+1) = term(i)*x/i; sum(i+1) = sum(i) + term(i+1); end % Display the results disp(‘i term(i) sum(i)’) a = 1: n+1; [a’ term’ sum’]

n Truncation Error term sum n term sum

n Truncation Error term sum How to reduce error? n term sum

Round-off Errors § Computers can represent numbers to a finite precision § Most important for real numbers integer math can be exact, but limited § How do computers represent numbers? § Binary representation of the integers and real numbers in computer memory

32 bits (23, 8, 1) 28 = 256 64 bits (52, 11, 1) 211 = 2048 MATLAB uses double precision

Order of operation Addition problem: exact result with 3 -digit arithmetic: Round-off error

Cancellation error If b is large, r is close to b Difference of two numbers very close to each other potential for greater error! Rationalize:

Try b = 97 (r = 96. 9794) x 2 (3 sig. figs. ) exact: 0. 01031 standard: 0. 01050 rationalized: 0. 01031 Corresponding to “cancellation, critical arithmetic”

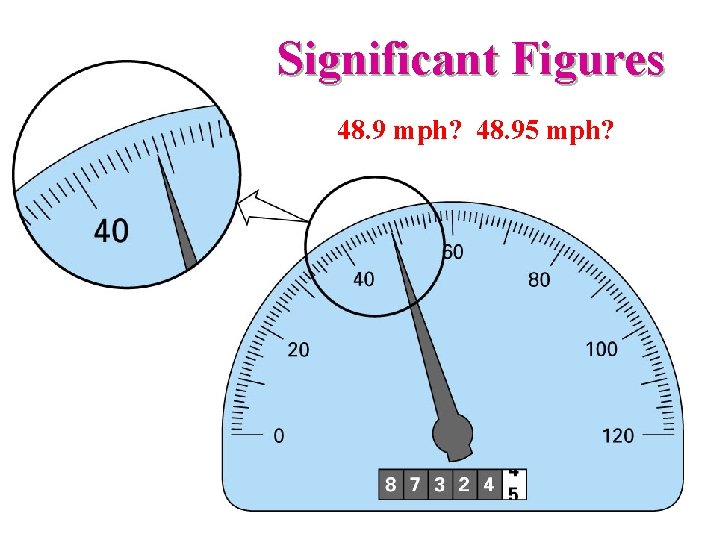
Significant Figures 48. 9 mph? 48. 95 mph?

Significant Digits § § The places which can be used with confidence 32 -bit machine: 7 significant digits 64 -bit machine: 17 significant digits Double precision: reduce round-off error, but increase CPU time

False Significant Figures 3. 25/1. 96 = 1. 65816326530162. . . (from MATLAB) But in practice only report 1. 65 (chopping) or 1. 66 (rounding)! Why? ? Because we don’t know what is beyond the second decimal place

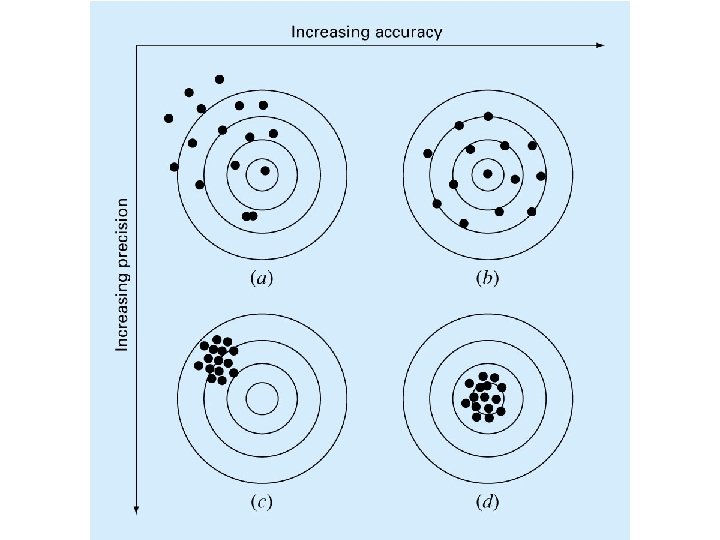
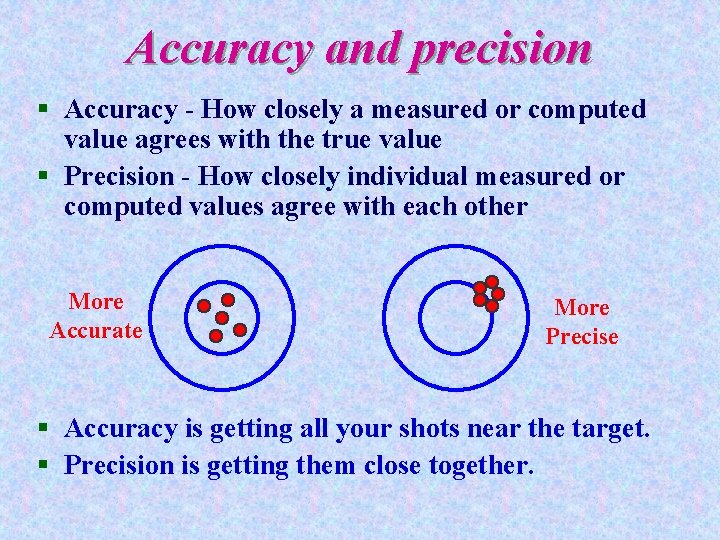
Accuracy and precision § Accuracy - How closely a measured or computed value agrees with the true value § Precision - How closely individual measured or computed values agree with each other More Accurate More Precise § Accuracy is getting all your shots near the target. § Precision is getting them close together.

Numerical Errors The difference between the true value and the approximation Approximation = true value + true error Et = true value approximation = x* x or in percent

Approximate Error § But the true value is not known § If we knew it, we wouldn’t have a problem § Use approximate error

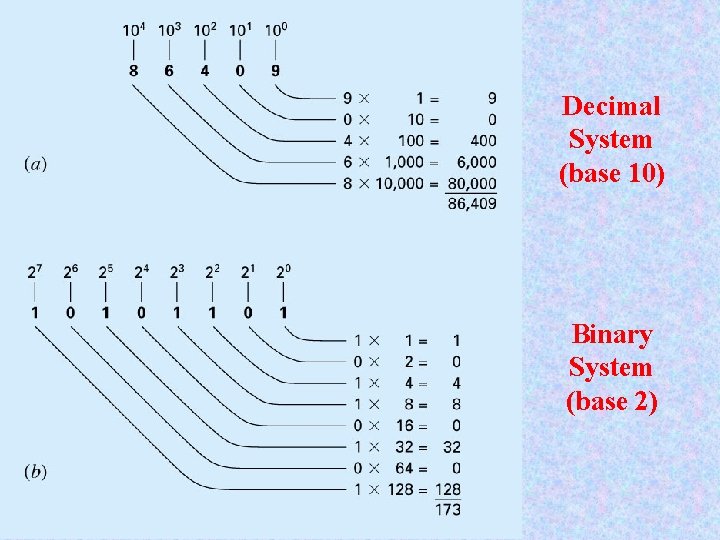
Number Systems § § Base-10 (Decimal): 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 Base-8 (Octal): 0, 1, 2, 3, 4, 5, 6, 7 Base-2 (Binary): 0, 1 – off/on, close/open, negative/positive charge Other non-decimal systems § 1 lb = 16 oz, 1 ft = 12 in, ½”, ¼”, …. .

Decimal System (base 10) Binary System (base 2)

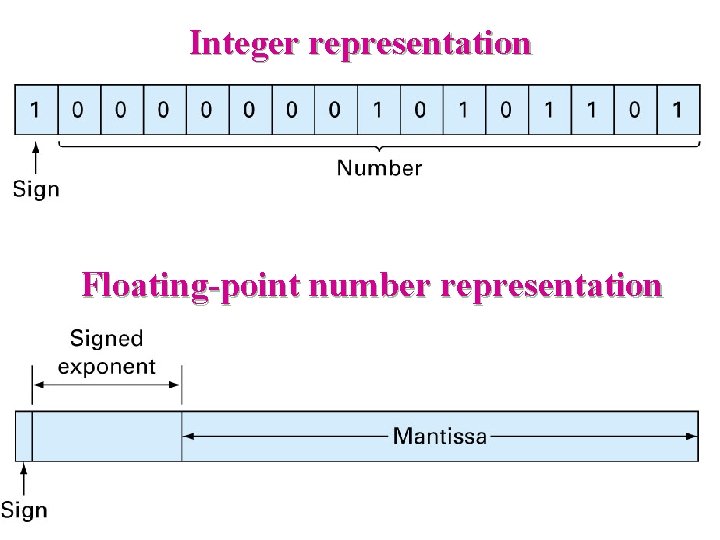
Integer Representation Signed magnitude method § Use the first bit of a word to indicate the sign – 0: negative (off), 1: positive (on) § Remaining bits are used to store a number + Sign 1 0 0 1 1 0 Number off / on, close / open, negative / positive

Integer Representation § 8 -bit word Sign § § Number +/- 0000000 are the same, therefore we may use “ -0” to represent “-128” Total numbers = 28 = 256 (-128 127)

Integer Representation 16 -bit word § Range: -32, 768 to 32, 767 § Overflow: > 32, 767 (cannot represent 43, 000 A&M students) § Underflow: < -32, 768 (magnitude too large) 32 -bit word § § Range: -2, 147, 483, 648 to 2, 147, 483, 647 9 significant digits Overflow: world population 6 billion Underflow: budget deficit -$100 billion

Integer Operations § § Integer arithmetic can be exact as long as you don't get remainders in division 7/2 = 3 in integer math § § or overflow the maximum integer For a 8 -bit computer max = 128 (or -127) § So 123 + 45 = overflow § and -74 * 2 = underflow

Floating-Point Representation § § § Real numbers (also called floating-point numbers) are represented differently For fraction or very large numbers Store as signed exponent § § § mantissa sign is 1 or 0 for negative or positive exponent is maximum value (positive or negative) of base mantissa contains significant digits

Floating-Point Representation sign of number § § signed exponent mantissa m: mantissa B: Base of the number system e: “signed” exponent Note: the mantissa is usually “normalized” if the leading digit is zero

Integer representation Floating-point number representation

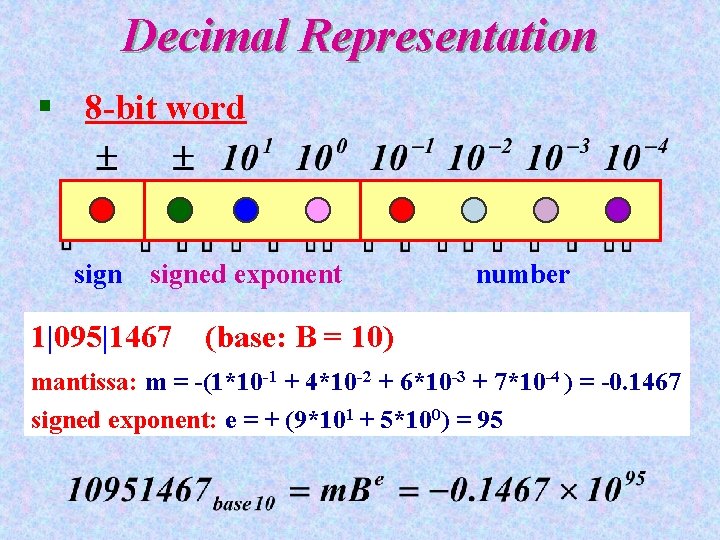
Decimal Representation § 8 -bit word signed exponent 1|095|1467 number (base: B = 10) mantissa: m = -(1*10 -1 + 4*10 -2 + 6*10 -3 + 7*10 -4 ) = -0. 1467 signed exponent: e = + (9*101 + 5*100) = 95

Floating-Point Representation § 8 -bit word (without normalization) signed exponent 0|111|0101 number (base: B = 2) mantissa: m = +(0*2 -1 + 1*2 -2 + 0*2 -3 + 1*2 -4 ) = 5/16 signed exponent: e = - (1*21 + 1*20) = -3

Normalization (Less accurate) (Normalization) § Remove the leading zero by lowering the exponent (d 1 = 1 for all numbers) § if m < 1/2, multiply by 2 to remove the leading 0 § floating-point allow fractions and very large numbers to be represented, but take up more memory and CPU time

Binary Representation § 8 -bit word (with normalization) signed exponent 1|011|1001 number (base: B = 2) mantissa: m = -(1*2 -1 + 0*2 -2 + 0*2 -3 + 1*2 -4 ) = -9/16 signed exponent: e = + (1*21 + 1*20) = 3

Single Precision § A real variable (number) is stored in four words, or 32 bits (64 bits for Supercomputers) § bit (binary digit): 0 or 1 § byte: 4 bits, 24 = 16 possible values § word: 2 bytes = 8 bits, 28 = 256 possible values 23 for the digits 32 bits 8 for the signed exponent 1 for the sign

Double Precision § A real variable is stored in eight words, or 64 bits § 16 words, 128 bits for supercomputers 52 for the digits 64 bits 11 for the signed exponent 1 for the sign § signed exponent 210 = 1024

Round-off Errors § Floating point characteristics contribute to round-off error (limited bits for storage) § Limited range of quantities can be represented § A finite number of quantities can be represented § The interval between numbers increases as the numbers grow § Example - three significant digits 0. 0100 0. 0101 0. 0102 …… 0. 0999 (0. 0001 increment) 0. 100 0. 101 0. 102 ……. 0. 999 (0. 001 increment) 1. 00 1. 01 1. 02 ……. 9. 99 (0. 01 increment)

MATLAB § Finite number of real quantities (integers, real numbers or text) can be represented § For 8 -bit, 28 = 256 quantities § For 16 -bit, 216 = 65536 quantities § MATLAB uses double precision § 4 bytes = 64 bits § more than 1019 (264) quantities