Review Error correction and error detection What is











- Slides: 11

• Review

• Error correction and error detection. • What is an error? Bits missed or altered. • How to find an error? – Make sure that when errors occur, the resulting message is invalid. – E. g: two bits message 00, 01, 10, 11 or 00, 11?

• How to find an error? – Introducing redundancy -- using 2 bits message to send 1 bit information in the previous example. – Message = information bits + redundant bits (checksum). • How to design codes that have error correction/detection capability? • Hamming distance between two code words: the number of different bits between the two code words. – E. g 010101 and 111000? Hamming distance = ? • Hamming distance of a complete code: the minimum Hamming distance any of the two codewords in the code. – E. g 010101, 111000, 000111, 111111 Hamming_distance= ?

– Relation between Hamming distance of a code and the code’s error detection/correction capability • Hamming distance = N • How many bits of errors can be detected? • How many bits of errors can be corrected? Example: 0000, 00001111, 11110000, 1111. Hamming distance = ? How many bits of errors can be detected? How many bits of errors can be corrected? Example 2: Parity code (Even parity code)? Let number of information bits = 2, How to construct the even parity code? Hamming distance = ?

– Error correction code: • How many (r) redundant bits do we need to correct a single error for the m information bits? – – A message contains m+r bits total number of possible codewords: 2^(m+r) total number of valid codewords = 2^(m) To correct single error, each single error must results in a different (invalid) codeword. – Total number of (invalid) codewords for one bit error = (m+r)2^m – total number of valid codewords plus the total number of (invalid) codewords for single bit error must be less than the total number of possible codewords. 2^m+(m+r)2^m <= 2^(r+m) m+r+1 <= 2^r

– Error correction code: • How many (r) redundant bits do we need to correct single error for the m information bits? m+r+1 <= 2^r m = 1, m = 2, m = 3, …… m = 1000, r=2 r=3 r = 10 • This formula gives the lower bound of the redundant bits to correct a single error. Hamming code achieves this lower bound (Chapter 3. 2. 1). – How many redundant bits are needed to detect a single error?

– Error correction code/error detection code: which code is more efficient? • Consider only the single bit error: – Assumption: error rate 10^(-6), one error in 1 million bits – packet size 1000 bits for information, total 1000 packets. – Error correction: 1000* (1000+10) – Error detection: 1000*(1000+1) + (1000+1) • Error correction code is in general NOT efficient!!!

• Error detection code: – parity code: detect single error, not good enough. – To detect N errors, we need to have a code whose hamming distance >=N+1. How to get this kind of code? – The most commonly used error detection code is called polynomial code, or cyclic redundancy code or CRC code. A bit stream is treated as a polynomial with coefficients 0 s and 1 s k bits => k-terms polynomial 11001 ---> x^4+x^3+0*x^2+0*x^1+x^0 The sender and the receiver have a generator polynomial G(X) with degree r Add the checksum bits to make sure that the final message is divisible by G(X).

• How to compute the checksum? • Let r be the degree of G(x). Append r zero to the low -order end of data bits (m bits) so that the frame contains m+r bits corresponding to x^r*M(x) • Using modulo 2 division to divide the bit stream corresponding to x^r*M(x) by the bit stream string corresponding to G(x). • Add the remainder back to the frame x^r*M(x). – Example: Data: 1101011011, Generator: 10011 – What would be the final data frame?

• The power of the CRC code – Depends on the selection of the generator, G(x) – T(x): frame polynomial, – E(x) error polynomial – G(x) generator polynomial – T(x) + E(x) / G(x) == E(x) / G(x) – Single error: E(x) = x^j » G(x) has more than two terms, guarantee to detect single error. – Double error: E(x) = x^j+x^k=x^k(x^(j-k)+1) » x^k+1 (k<32768) cannot be divisiable by x^15+x^14+1. – x+1 cannot divide any polynomial with odd number of terms (detect all odd number of errors). – x^r+…+ can detect all less than r number of burst errors.

• Three standard polynomials: – CRC-12 = x^12+x^11+x^3+x^2+x+1 – CRC-16 = x^16+x^15+x^2+1 – CRC-CCITT = x^16+x^12+x^5+1 • What is the hamming distance for the code generated by CRC-16?
 Difference between error detection and error correction
Difference between error detection and error correction Error detection and correction in computer networks
Error detection and correction in computer networks Error detection and correction in data link layer
Error detection and correction in data link layer Cyclic redundancy check
Cyclic redundancy check 해밍코드 인코더
해밍코드 인코더 Error detection and correction
Error detection and correction Error detection and correction in networking
Error detection and correction in networking Error detection and correction in computer networks
Error detection and correction in computer networks Error correction
Error correction Stata vec
Stata vec Eror
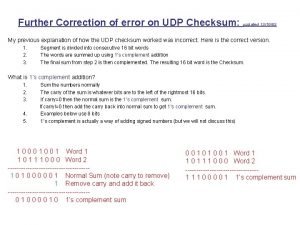
Eror Udp error correction
Udp error correction