RUANG VEKTOR Trihastuti Agustinah Vektor pada Rn Definisi


































- Slides: 41

RUANG VEKTOR Trihastuti Agustinah.

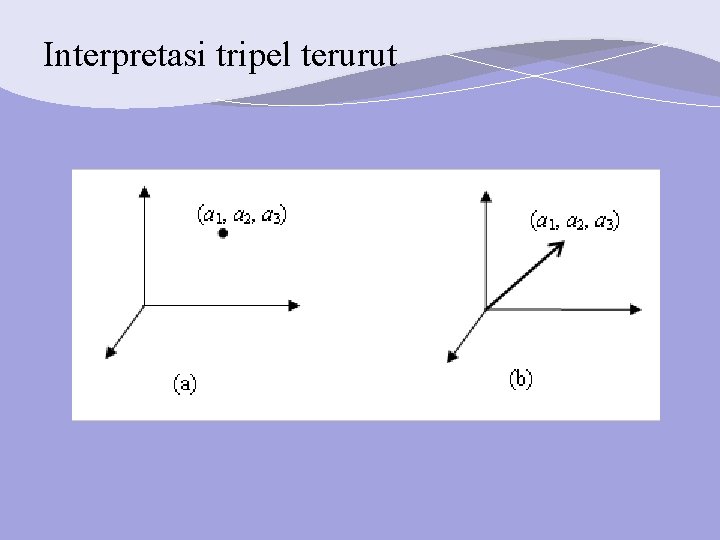
Vektor pada Rn • Definisi Ruang-n – Himpunan seluruh tupel-n dari bilangan real • Notasi: Rn – n = 2 pasangan terurut; – n = 3 triple terurut – n = 1 satu bilangan real (notasi: R 1 atau R) • 2 interpretasi geometris tripel terurut (a 1, a 2, a 3): – Titik: a 1, a 2, a 3 sebagai koordinat – Vektor: a 1, a 2, a 3 sebagai komponen vektor

Interpretasi tripel terurut

Operasi standar • Dua vektor u=(u 1, u 2, ···, un) dan v=(v 1, v 2, ···, vn) pada Rn – Sama u=v; u 1= v 1, u 2= v 2, ···, un= vn – Jumlah: u+v = (u 1+v 1, u 2+v 2, ···, un+vn) – Perkalian skalar: ku=(ku 1, ku 2, ···, kun) • Vektor nol Notasi: 0 0 = (0, 0, ···, 0)

Sifat-sifat aritmatika • Jika u=(u 1, u 2, ···, un), v=(v 1, v 2, ···, vn) pada Rn – Negatif: -u = (-u 1, -u 2, ···, -un) – Selisih: v- u = v + (- u) atau v- u = (v 1 -u 1, v 2 -u 2, ···, vnun) • Teorema: (k, l: skalar) § v+ u = u +v k(l u) = (kl) u § u + (v+w) = (u +v) + w k(u +v) = k u + kv § u + 0 = 0+ u = u (k+l) u = ku+lu § u +(- u)= 0 u - u = 0 1 u = u

Ruang n-Euclidean • Misal u=(u 1, u 2, ···, un), v=(v 1, v 2, ···, vn), w=(w 1, w 2, ···, wn) adalah vektor pada Rn dan k skalar • Hasilkali-dalam (inner-product) Euclidean: u·v = (u 1 v 1 + u 2 v 2 + ··· + unvn) • 4 sifat penting inner product u·v = v·u (u+v)·w = uw + vw (ku)·v = k(u·v) v·v ≥ 0, v·v = 0 jika dan hanya jika (iff) v = 0

Contoh 1 • Dapatkan hasilkali-dalam Euclidean dari vektor: u = (-1, 3, 5, 7) dan v = (5, -4, 7, 0) u·v = (-1)(5) + (3)(-4) + (5)(7) + (7)(0) = 18 • Cara penghitungan hasilkali-dalam sama dengan perkalian aritmatika biasa (3 u+2 v)·(4 u+v) = (3 u)·(4 u+v) + (2 v)·(4 u+v) = (3 u)·(4 u) + (3 u)·v + (2 v)·(4 u) + (2 v)·v = 12(u·u) + 11(u·v) + 2(v·v)

Norm dan jarak • Definisi norm atau panjang Euclidean untuk vektor u=(u 1, u 2, ···, un): • Definisi jarak (distance) antara titik u=(u 1, u 2, ···, un) dan v=(v 1, v 2, ···, vn):

Pertidaksamaan Cauchy-Schwarz • Vektor u=(u 1, u 2, ···, un), v=(v 1, v 2, ···, vn) pada Rn • Pertidaksamaan Cauchy-Schwarz: atau

Sifat-sifat norm dan jarak • Jika u dan v adalah vektor dan k skalar ü ||u|| ≥ 0 ü ||u|| = 0 iff u =0 ü ||ku|| = |k| ||u|| perkalian vektor dgn skalar mengalikan panjang dr vektor sebesar k ku u u+v v u ü ||u +v|| ≤ ||u||+||v|| jumlah dua sisi segitiga lebih kecil atau sama dengan sisi ketiga dr segitiga tersebut

Vektor ortogonal • Dua vektor u dan v adalah ortogonal iff u·v=0 • Vektor u, v dan u+v membentuk sisi-sisi segitiga u+v u • Teorema Phytagoras ||u+v||2=||u||2+||v||2 v

Ruang Vektor Real • Definisi ruang vektor V: – himpunan objek di mana dua operasi berikut didefinisikan pada V • jumlah dari pasangan objek dalam V • perkalian objek dengan skalar • Jika aksioma –aksioma untuk ruang vektor terpenuhi oleh seluruh objek u, v, w dalam V dan skalar k dan l, maka • V disebut ruang vektor • objek dalam V disebut vektor.

Aksioma-aksioma • Jika u dan v adalah objek dalam V, maka u + v juga objek dalam V – u+v=v+u – u +(v +w) = (u+ v) + w • Objek 0 dalam V disebut vektor nol untuk V – 0+u=u+ 0=u untuk semua u dalam V • Untuk tiap u dalam V, objek –u dalam V disebut negatif dari u – u + (- u) = (- u) + u = 0 • Jika k adalah skalar sebarang dan u adalah objek dalam V, maka ku juga dalam V – k(u +v) = ku + kv – k(l u) = (kl) u – 1 u = u

Bukti • Misal

Subspace (subruang) • Definisi: – Subset W dari ruang vektor V disebut subspace dari V jika W merupakan ruang vektor yang dibentuk dari operasi penjumlahan dan perkalian dalam V • Bila W adalah himpunan yang terdiri dari satu vektor atau lebih dari ruang vektor V, maka W subspace dari V iff – Jika u dan v vektor dalam W, maka u+v juga dalam W – Jika k sebarang skalar dan u adalah sebarang vektor dalam W, maka ku juga dalam W

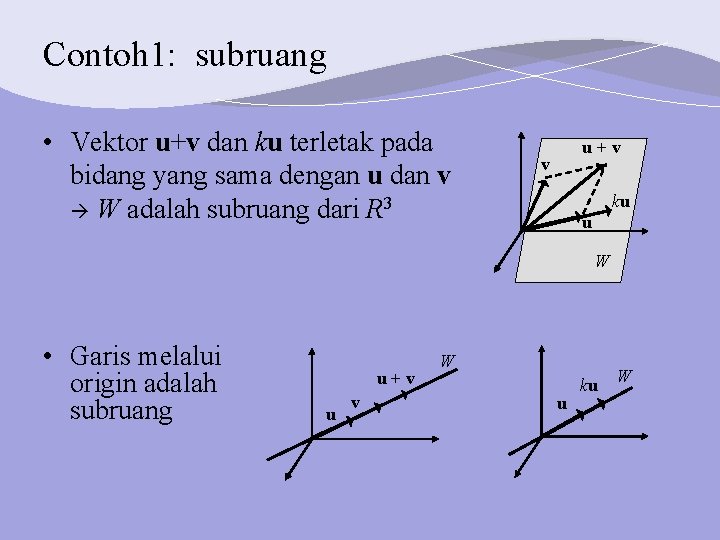
Contoh 1: subruang • Vektor u+v dan ku terletak pada bidang yang sama dengan u dan v W adalah subruang dari R 3 u+v v ku u W • Garis melalui origin adalah subruang u+v u v W u ku W

Subruang dari R 2 dan R 3 • Tiap ruang vektor tak-nol V minimal terdiri dari 2 subruang: – Subruang V – Vektor nol dalam V subruang nol (zero subspace) • Subruang dari R 2 Ø Ø Ø {0} Garis melalui origin R 2 • Subruang dari R 3 Ø Ø {0} Garis melalui origin Bidang melalui origin R 3

Kombinasi linear dari vektor • Vektor w adalah kombinasi linear dari v 1, v 2, , vr dan k 1, k 2, , kr jika • Untuk r = 1: Ø Ø w = k 1 v 1 Kombinasi linear vektor tunggal v 1 • Vektor v=(a, b, c): kombinasi linear dari vektor basis standar

Contoh 2 • Vektor u = (1, 2, -1) dan v = (6, 4, 2) Tunjukkan bahwa ü w=(9, 2, 7): kombinasi linear dari u dan v ü w´=(4, -1, 8): bukan kombinasi linear • w kombinasi linear dari u dan v bila w = k 1 u + k 2 v (9, 2, 7) = k 1(1, 2, -1) + k 2(6, 4, 2) (9, 2, 7) = k 1+6 k 2, 2 k 1+4 k 2, -k 1+2 k 2 k 1 + 6 k 2 = 9; 2 k 1 + 4 k 2 = 2; -k 1 + 2 k 2 = 7 → k 1=-3; k 2=2 Maka w = -3 u + 2 v

Rentangan (spanning) • Jika v 1, v 2, , vr adalah vektor dalam ruang vektor V, maka – Himpunan W dari seluruh kombinasi linear v 1, v 2, , vr adalah subruang V – W adalah subruang terkecil dalam V yang berisi v 1, v 2, , vr • Jika S = {v 1, v 2, , vr} adalah himpunan vektor dalam ruang vektor V, maka – Subruang W dari seluruh kombinasi linear v 1, v 2, , vr disebut ruang yang direntang oleh vektor tersebut – W= span (S) atau W= span {v 1, v 2, , vr}

• Jika v 1 dan v 2 adalah vektor di R 3 dengan titik awal pada origin – Span{v 1, v 2} yang berisi seluruh kombinasi linear k 1 v 1 + k 2 v 2: bidang melalui origin yang ditentukan oleh v 1 dan v 2 • Jika v merupakan vektor di R 2 atau R 3 – Span{v} yang berupa seluruh perkalian kv: garis yang ditentukan oleh v span{v 1, v 2} z k 1 v 1+ k 2 v 2 kv v 2 v v 1 x span{v} z k 1 v 1 y y x

Contoh 3 • Tunjukkan bahwa v 1 = (1, 1, 2), v 2 = (1, 0, 1), v 3 = (2, 1, 3) merentang ruang vektor pada R 3 • Tentukan vektor semu b=(b 1, b 2, b 3) sebagai kombinasi linear b = k 1 v 1 + k 2 v 2 + k 3 v 3 (b 1, b 2, b 3) = k 1(1, 1, 2) + k 2(1, 0, 1)+k 3(2, 1, 3) k 1 + k 2 + 2 k 3 = b 1 k 1 + k 3 = b 2 2 k 1 + k 2 + 3 k 3 = b 3 ü Sistem linear konsisten iff matriks koefisien A dapat diinverskan ü det(A)=0 → A tidak dapat diinverskan ü v 1, v 2 dan v 3 tidak dapat merentang pada R 3

Kebebasan linear • Himpunan vektor S = {v 1, v 2, , vr} • Persamaan vektor k 1 v 1 + k 2 v 2 + + krvr = 0 • Jika hanya ada satu solusi – k 1= 0, k 2 = 0, , kr = 0 – S adalah himpunan bebas linier (linearly independent) • Jika ada solusi yang lain – S disebut himpunan takbebas linear

Contoh 4 • Tunjukkan bahwa v 1 = (1, -2, 3), v 2 = (5, 6, -1), v 3 = (3, 2, 1) membentuk himpunan bebas linear atau tak bebas linear • Persamaan vektor dalam komponen k 1 v 1 + k 2 v 2 + k 3 v 3 = 0 k 1(1, -2, 3) + k 2(5, 6, -1)+k 3(3, 2, 1)=(0, 0, 0) (k 1+5 k 2+3 k 3, – 2 k 1+6 k 2+2 k 3, 3 k 1– k 2 +k 3) = (0, 0, 0) • Persamaan untuk tiap komponen k 1 + 5 k 2 + 3 k 3 = 0 – 2 k 1 + 6 k 2 + 2 k 3 = 0 3 k 1 – k 2 + k 3 = 0

Contoh 4 (cont. ) • Solusi sistem k 1= t/2; k 2 = -t/2; k 3 = t • Solusi nontrivial • v 1, v 2 dan v 3: himpunan takbebas linear • Eksistensi solusi nontrivial ü Determinan matriks koefisien sama dengan nol ü Matrik tsb tidak dapat diinverskan

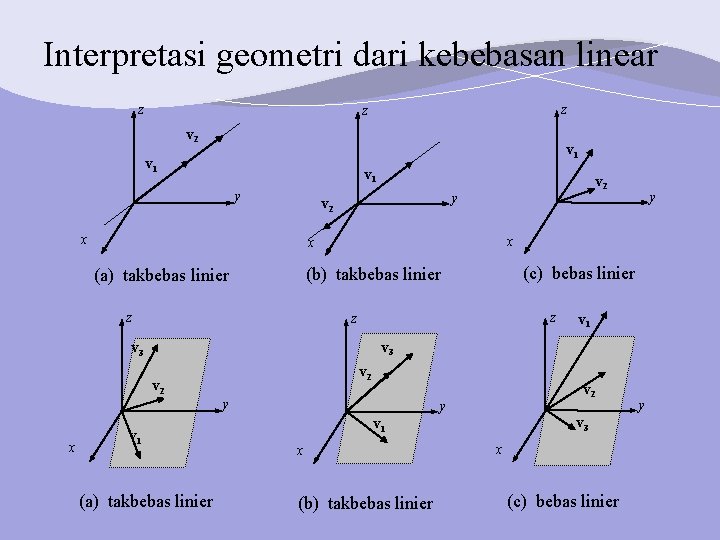
Interpretasi geometri dari kebebasan linear z z z v 2 v 1 v 1 y y v 2 x (c) bebas linier (b) takbebas linier z y x x (a) takbebas linier z z v 1 v 3 v 2 y x v 2 v 1 (a) takbebas linier v 2 y v 3 v 1 x (b) takbebas linier x (c) bebas linier y

Basis • Definisi: – Jika V adalah ruang vektor – S = {v 1, v 2, , vn}: himpunan vektor dalam V – S disebut basis untuk V jika memenuhi kondisi berikut • S adalah bebas linear • S merentang V (S spans V) • Teorema: – Jika S = {v 1, v 2, , vn}: basis untuk ruang vektor V – Tiap vektor v dalam V dapat dinyatakan sebagai kombinasi linear dari vektor-vektor dalam S dalam satu cara saja

Basis • Bukti: v = c 1 v 1+ c 2 v 2+ + cnvn dan v = k 1 v 1+ k 2 v 2+ + knvn • Kurangkan kedua persamaan 0 = (c 1– k 1)v 1+ (c 2 – k 2)v 2+ + (cn – kn)vn • Solusi: c 1= k 1, c 2 = k 2, , cn = kn • Kedua ekspresi untuk v adalah sama

Dimensi • Definisi: – Ruang vektor tak nol V disebut dimensi berhingga – Bila V berisi himpunan vektor-vektor berhingga {v 1, v 2, , vn} yang membentuk sebuah basis – Jika tidak terdapat himpunan vektor tersebut, V disebut dimensi tak berhingga • Teorema: – Jika V adalah ruang vektor dimensi berhingga dan {v 1, v 2, , vn} merupakan basis • Tiap himpunan yang memiliki vektor > n takbebas linear • Himpunan vektor < n tidak dapat merentang V

Dimensi • Catatan: – Bila S = {v 1, v 2, , vn} adalah basis untuk V – Seluruh basis untuk V memiliki jumlah vektor yang sama dengan basis S – Basis untuk Rn memiliki n vektor – Basis untuk R 3 memiliki 3 vektor – Basis untuk R 2 memiliki 2 vektor – Basis untuk R 1 memiliki 1 vektor – Jumlah vektor dalam basis = jumlah dari dimensi

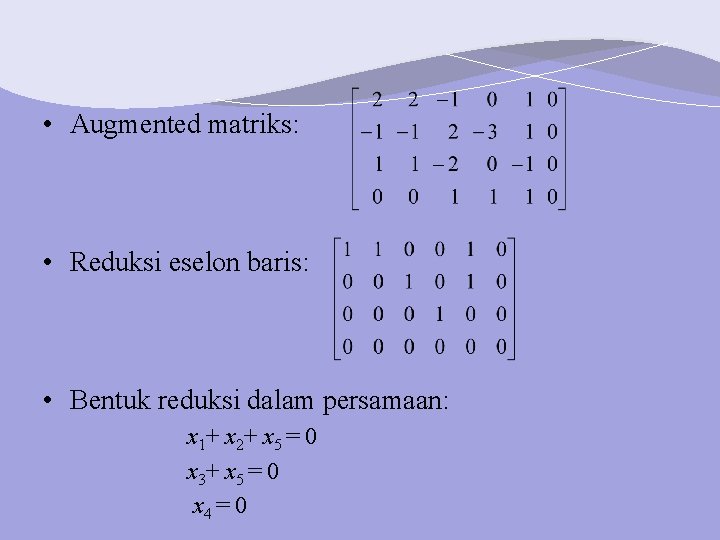
Contoh 5 • Tentukan basis dan dimensi untuk solusi ruang sistem homogen berikut: 2 x 1 + 2 x 2 – x 3 + x 5 = 0 – x 1 – x 2 + 2 x 3 – 3 x 4 + x 5 = 0 x 1 + x 2 – 2 x 3 – x 5 = 0 x 3 + x 4 + x 5 = 0

• Augmented matriks: • Reduksi eselon baris: • Bentuk reduksi dalam persamaan: x 1+ x 2+ x 5 = 0 x 3+ x 5 = 0 x 4 = 0

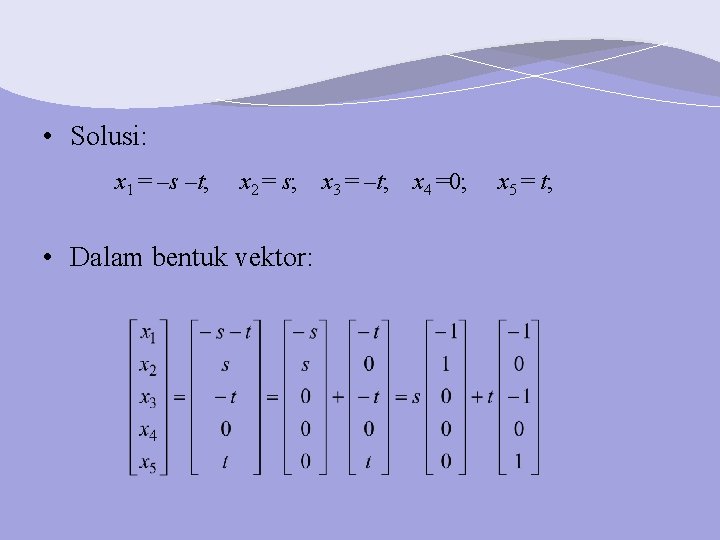
• Solusi: x 1 = –s –t; x 2 = s; • Dalam bentuk vektor: x 3 = –t; x 4 =0; x 5 = t;

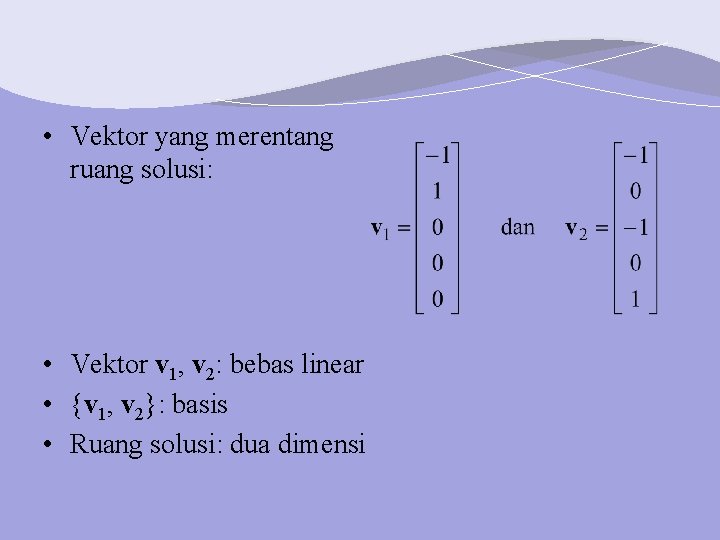
• Vektor yang merentang ruang solusi: • Vektor v 1, v 2: bebas linear • {v 1, v 2}: basis • Ruang solusi: dua dimensi

Ruang baris, kolom dan nul • Jika A matriks m×n: – subruang Rn direntang oleh vektor baris disebut ruang baris dari A – subruang Rm direntang oleh vektor kolom disebut ruang kolom dari A – ruang solusi dari sistem homogen dari persamaan Ax = 0 yang merupakan subruang Rn disebut ruang nul dari A • Teorema: – Sistem persamaan linear Ax = b adalah konsisten iff b merupakan ruang kolom dari A

Contoh 6 • Tunjukkan bahwa b merupakan ruang kolom dari A dan ekspresikan b sebagai kombinasi linear dari vektor kolom matriks A:

Contoh 6 (cont. ) • Solusi sistem: x 1 = 2; x 2 = – 1; x 3 = 3 • Sistem konsisten b merupakan ruang kolom A • Ekspresi b sebagai kombinasi linear vektor kolom matriks A

Basis untuk ruang baris, kolom dan nul • Operasi baris elementer tidak mengubah ruang nul dan ruang baris dari matriks • Jika matriks R merupakan matriks hasil reduksi baris: – Vektor baris dengan leading 1 (baris tak nol) basis untuk ruang baris – Vektor kolom dengan leading 1 basis untuk ruang kolom

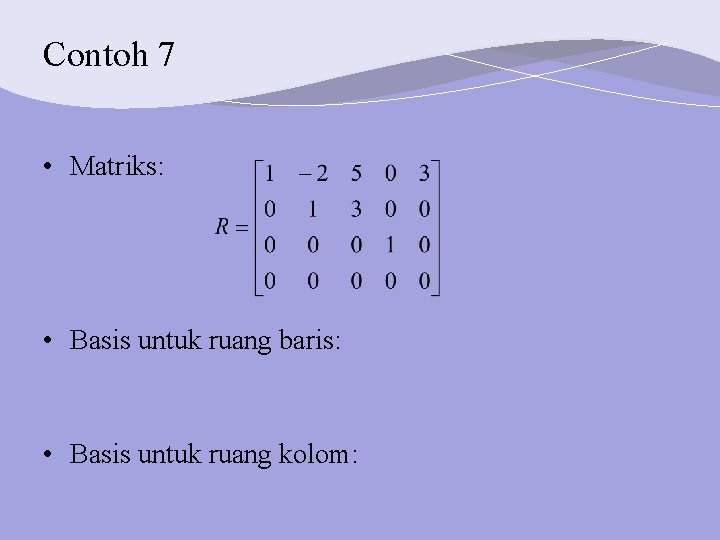
Contoh 7 • Matriks: • Basis untuk ruang baris: • Basis untuk ruang kolom:

Rank dan nullity • Rank: dimensi dari ruang baris dan ruang kolom • Notasi: rank(A) • Nulitas(nullity): dimensi dari ruang nul • Notasi: nullity(A) • rank(A)=dim(ruang baris A)=dim(ruang kolom AT) • rank(A) + nullity(A) = n • Jumlah var. leading + jumlah var. bebas = n

Nilai maksimum dari rank • Jika A matriks m×n: – rank(A) = jumlah var. leading dalam solusi Ax = 0 – nullity(A) = jumlah parameter dalam solusi Ax = 0 – Vektor baris terletak pada Rn ruang baris berdimensi n – Vektor kolom terletak pada Rm ruang kolom dimensi m – Ruang baris = ruang kolom – m n, rank(A) = nilai terkecil antara m dan n • Nilai maksimum rank: – rank(A) min(m, n)
 Diketahui vektor-vektor sebagai berikut. gambarlah vektor:
Diketahui vektor-vektor sebagai berikut. gambarlah vektor: Sistem koordinat vektor
Sistem koordinat vektor Ciri ciri kubus
Ciri ciri kubus Sebutkan ruang lingkup sistem informasi manajemen
Sebutkan ruang lingkup sistem informasi manajemen Ruang lingkup pembahasan psikometri
Ruang lingkup pembahasan psikometri Ciri-ciri akuntansi biaya
Ciri-ciri akuntansi biaya Teori laba friksional
Teori laba friksional Campuran yang
Campuran yang Kepelbagaian makanan etnik pemangkin perpaduan
Kepelbagaian makanan etnik pemangkin perpaduan Pembagian ruang-ruang hardisk secara logikal dinamakan ?
Pembagian ruang-ruang hardisk secara logikal dinamakan ? 4 contoh notasi vektor
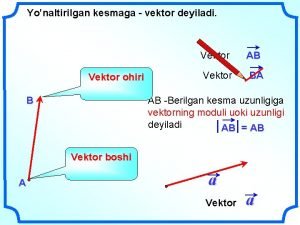
4 contoh notasi vektor Vektor basis
Vektor basis Vektor tegak lurus
Vektor tegak lurus Ruang vektor umum
Ruang vektor umum Contoh soal turunan vektor
Contoh soal turunan vektor Jika vektor v=xi+yj-zk panjang vektor v adalah
Jika vektor v=xi+yj-zk panjang vektor v adalah Vektor dikali skalar
Vektor dikali skalar Karakteristik penggabungan gambar vektor dan bitmap
Karakteristik penggabungan gambar vektor dan bitmap Peta konsep operasi vektor pada r3
Peta konsep operasi vektor pada r3 Mi a vektor fogalma
Mi a vektor fogalma Penyakit vektor
Penyakit vektor Teorema pythagoras berlaku pada bangun datar
Teorema pythagoras berlaku pada bangun datar Ruang peta dan nulitas pada transformasi
Ruang peta dan nulitas pada transformasi Banyak sisi pada bangun ruang balok adalah
Banyak sisi pada bangun ruang balok adalah Tekanan zat padat
Tekanan zat padat Tekanan pada zat cair
Tekanan pada zat cair Sisi pada kubus dibatasi oleh
Sisi pada kubus dibatasi oleh Proyeksi sekalar vektor a = (-1, 3) pada b = (6, 0) adalah
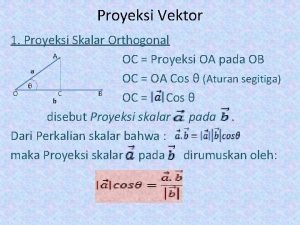
Proyeksi sekalar vektor a = (-1, 3) pada b = (6, 0) adalah Pengertian proyeksi skalar ortogonal
Pengertian proyeksi skalar ortogonal Operasi dasar vektor
Operasi dasar vektor A-b vektor
A-b vektor Perkalian vektor
Perkalian vektor Sumbu koordinat pada java menyatakan titik (0,0) pada
Sumbu koordinat pada java menyatakan titik (0,0) pada Perintah yang digunakan untuk membuat grafik adalah
Perintah yang digunakan untuk membuat grafik adalah Hati hendak semua jadi
Hati hendak semua jadi Trakeolus
Trakeolus Pembentukan mikrospora pada tumbuhan berbunga terjadi pada
Pembentukan mikrospora pada tumbuhan berbunga terjadi pada Salah satu aturan garis ukur?
Salah satu aturan garis ukur? Uhcd adalah
Uhcd adalah Mulut pada sipuncula terdapat pada bagian
Mulut pada sipuncula terdapat pada bagian Sambungan pada rel kereta api di
Sambungan pada rel kereta api di Penulisan alamat absolut mutlak yang benar adalah
Penulisan alamat absolut mutlak yang benar adalah