RUANG VEKTOR Vektor segmensegmen garis terarah atau panahpanah

RUANG VEKTOR

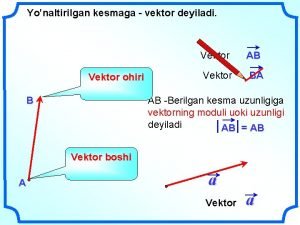
• Vektor : segmen-segmen garis terarah atau panah-panah di ruang-2 atau ruang-3 atau Rn; arah panah menentukan arah vektor dan panjang panah menyatakan besarnya. • Ekor panah dinamakan titik awal (initial point) dari vektor, dan ujung panah dinamakan titik terminal (terminal point). • Vektor akan dinyatakan dengan huruf kecil tebal misalnya, a, v, w, dan x. Bila membahas vektor, maka bilangan akan dinyatakan sebagai skalar. Semua skalar merupakan bilangan riil dan akan dinyatakan oleh huruf kecil biasa misalnya, k, dan l.

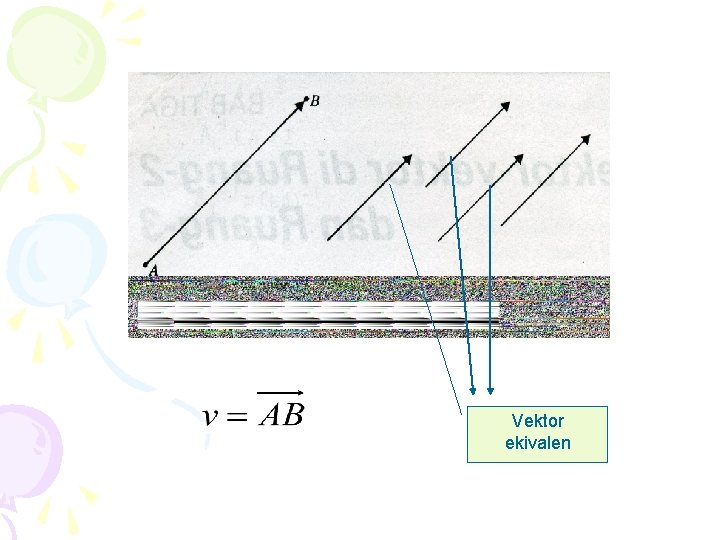
Vektor ekivalen

• Jika, titik awal vektor v adalah A dan titik terminalnya adalah B, maka kita tuliskan • Vektor-vektor yang mempunyai panjang dan arah yang sama walaupun mungkin diletakkan pada kedudukan yang berbeda-beda, dinamakan ekivalen. Jika v dan w ekivalen maka kita tuliskan v = w • Dua vektor u = (u 1, u 2, . . . , un) dan v = (v 1, v 2, . . . , vn) pada Rn dinamakan sama jika u 1 = v 1, u 2 = v 2, . . . , un = vn

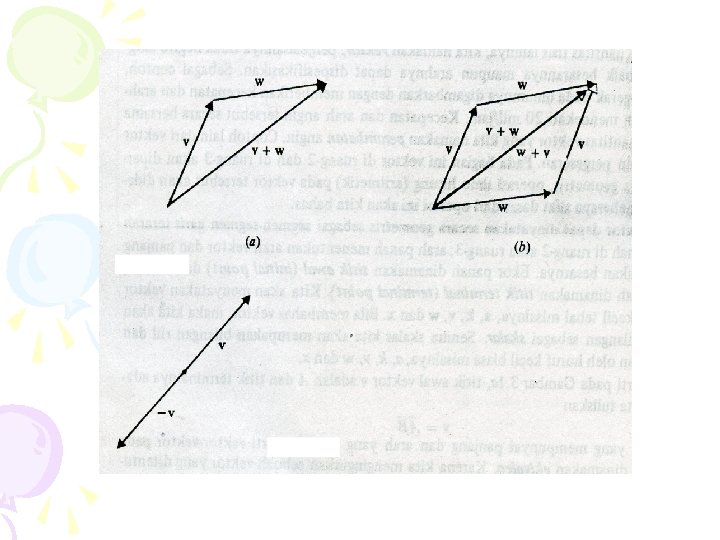
• Jika v dan w adalah sebarang dua vektor, maka v+w=w+v • Jika v adalah sebarang vektor yang tak nol, maka vektor w yang memenuhi v + w = 0 adalah negatif dari v w=-v

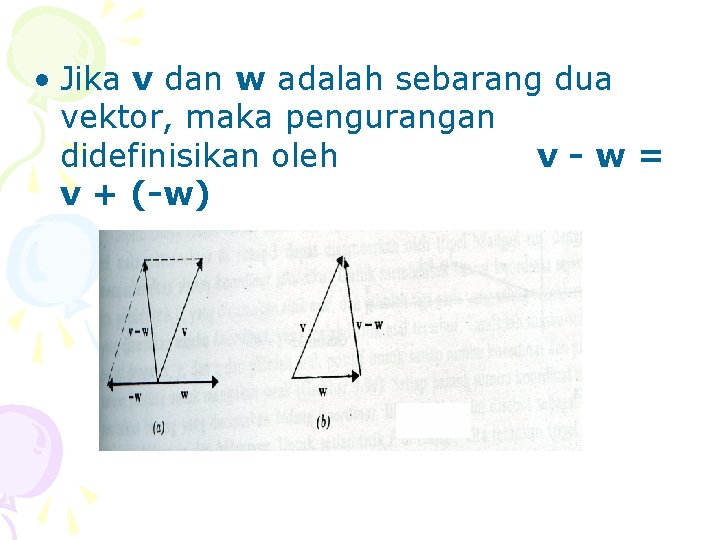
• Jika v dan w adalah sebarang dua vektor, maka pengurangan didefinisikan oleh v-w= v + (-w)

Koordinat-koordinat (v 1, v 2) dari titik terminal v dinamakan komponen dari v, dan kita menuliskannya sebagai v = (v 1, v 2)

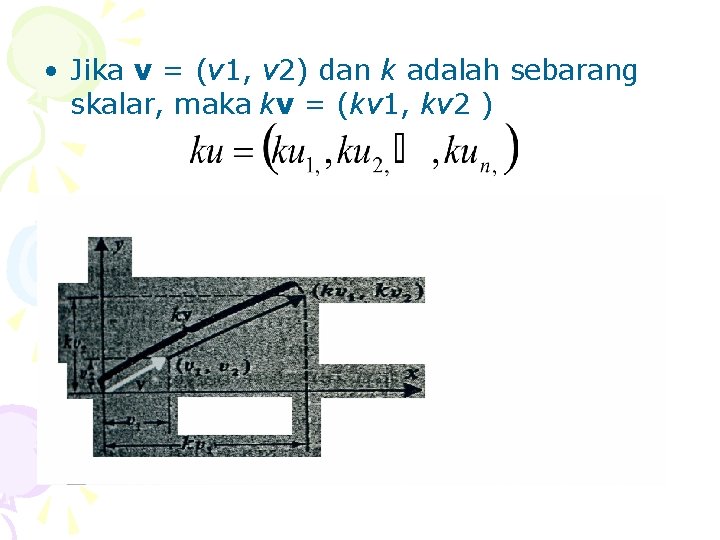
• Jika v = (v 1, v 2) dan k adalah sebarang skalar, maka kv = (kv 1, kv 2 )

NORMA VEKTOR • Terdiri dari 33 Teorema •

TEOREMA 1 • Jika u =(u 1, u 2, . . . , un), v = (v 1, v 2, . . . , vn) dan w = (w 1, w 2, . . . , wn) adalah vektor – vektor pada Rn dan k serta l adalah skalar , maka : – u + v = v +u – u + (v + w ) =(u + v) + w – u + 0= 0 +u = u – u + (-u) =0, yakni, u – u = 0 – k(lu) = (kl)u – k(u + v) = ku + kv – (k + l)u = ku + lu – lu = u

TEOREMA 1 • Panjang vektor v = norma dari v = v . vektor v = (v 1, v 2) di dalam ruang-2 adalah v = • Jika v adalah vektor dalam ruang-3, maka v =

Jika P 1 = (x 1, y 1, z 1) dan P 2 = (x 2, y 2, z 2) adalah dua titik didalam ruang-3, maka jarak diantara kedua titik tersebut adalah norma vektor

PANJANG DAN SUDUT DI RUANG HASIL KALI DALAM • Jika V adalah sebuah ruang hasil kali dalam, maka norma (atau panjang) vektor u dinyatakan oleh ||u|| dan didefinisikan oleh ||u|| = • Jika V adalah sebuah ruang hasil kali dalam, maka jarak antara dua titik (vektor) u dan v dinyatakan oleh d(u, v) dan didefinisikan oleh d(u, v) = ||u – v||

TEOREMA 2 Jika u, v, dan w adalah vektor pada dan k adalah sembarang skalar, maka : • u. v=v. u • (u + v). w = u. w + v. w • (ku). v = k(u. v) • v. v ≥ 0, Selanjutnya, v. v = 0 jika dan hanya jika v = 0

TEOREMA 3 Misalkan V adalah sebuah ruang vektor, u sebuah vektor pada V, dan k sebuah skalar; maka : • 0 u = 0 • k 0 = 0 • (-1)u = - u • jika ku = 0, maka k = 0 atau u = 0

TEOREMA 4 • Jika W adalah himpunan dari satu atau lebih vektor dari sebuah ruang vektor V, maka W adalah subruang dari V jika dan hanya jika kondisi berikut berlaku. • Jika u dan v adalah vektor-vektor pada W, maka u + v terletak di W. • Jika k adalah sebarang skalar dan u adalah sebarang vektor pada W, maka ku berada di W. Contoh soal

TEOREMA 4 • Sebuah vektor w dinamakan kombinasi linear dari vektor-vektor v 1, v 2, . . , vr jika vektor tersebut dapat diungkapkan dalam bentuk w = k 1 v 1 + k 2 v 2 +. . . + krvr • dimana k 1, k 2, . . , kr adalah skalar. • Jika v 1, v 2, . . . , vr adalah vektor-vektor pada ruang vektor V dan jika masing-masing vektor pada V dapat dinyatakan sebagai kombinasi linear v 1, v 2, . . , vr maka kita mengatakan bahwa vektor-vektor ini merentang V.

TEOREMA 5 • Jika v 1, v 2, . . , vr adalah vektor-vektor pada ruang vektor V, maka : • Himpunan W dari semua kombinasi linear v 1, v 2, . . , vr adalah subruang V. • W adalah subruang terkecil dari V yang mengandung v 1, v 2, . . , vr dalam arti bahwa setiap subruang lain dari V yang mengandung v 1, v 2, . . , vr harus mengandung W.

TEOREMA 6 • Himpunan S dengan dua vektor atau lebih adalah • Tak bebas linear jika dan hanya jika paling tidak satu diantara anggota himpunan vektor S dapat dinyatakan sebagai kombinasi linear dari anggota himpunan vektor S lainnya. • Bebas linear jika tidak ada anggota himpunan vektor S yang dapat dinyatakan sebagai kombinasi linear dalam anggota himpunan vektor S lainnya.

TEOREMA 6 • Jika S = {v 1, v 2, . . , vr} adalah himpunan vektor, maka persamaan vektor k 1 v 1 + k 2 v 2 +. . . + krvr = 0 • mempunyai paling sedikit satu pemecahan, yakni k 1 = 0, k 2 = 0, . . , kr = 0 • Jika ini adalah satu-satunya pemecahan, maka S kita namakan himpunan bebas linear (linearly independent). Jika ada pemecahan lain, maka S kita namakan himpunan tak bebas linear (linearly dependent).

TEOREMA 7 • Jika sebuah himpunan mengandung vektor nol, maka himpunan itu takbebas linear. • Sebuah himpunan yang mempunyai persis dua vektor takbebas linear jika dan hanya jika salah satu dari vektor itu adalah perkalian dari skalar lainnya.

TEOREMA 8 • Misalkan S = {v 1, v 2, . . , vr} adalah himpunan vektor-vektor pada Rn. Jika r > n, maka S takbebas linear.

TEOREMA 9 • Jika S = { v 1, v 2, . . , vn } adalah basis untuk ruang vektor V, maka setiap himpunan dengan lebih dari n vektor adalah takbebas linear.

TEOREMA 9 • Jika V adalah sebarang ruang vektor dan S = { v 1, v 2, . . , vr} merupakan himpunan berhingga dari vektor-vektor pada V, maka S kita namakan basis untuk V jika S bebas linear ; • S merentang V Sebuah ruang vektor taknol V dinamakan berdimensi berhingga (finite dimensional) jika ruang vektor tersebut mengandung sebuah himpunan berhingga dari vektor-vektor { v 1, v 2, . . , vn } yang membentuk sebuah basis. Jika tidak ada himpunan seperti itu, maka V dinamakan berdimensi takberhingga (infinite dimensionel). Tambahan lagi, kita akan menganggap ruang vektor nol sebagai ruang vektor berdimensi berhingga walaupun ruang vektor tersebut tidak mempunyai himpunan bebas linear, sehingga basispun tidak ada.

TEOREMA 10 • Sebarang dua basis untuk ruang vektor berdimensi berhingga mempunyai jumlah vektor yang sama.

• • • TEOREMA 11 Jika S = { v 1, v 2, . . , vn } adalah sebuah himpunan n vektor bebas linear pada sebuah ruang V yang berdimensi n, maka S adalah sebuah basis untuk V. Jika S = { v 1, v 2, . . , vn } adalah sebuah himpunan n vektor yang merentang ruang V yang berdimensi n, maka S adalah basis untuk V. Jika S = { v 1, v 2, . . , vn } adalah sebuah himpunan bebas linear pada ruang V yang berdimensi n dan r < n, maka S dapat diperbesar menjadi basis untuk V ; yakni, vektor-vektor vr+1 , . . , vn sehingga {v 1, v 2, , . . , vr+1, . . , vn} adalah sebuah basis untuk V.

RUANG BARIS DAN KOLOM MATRIKS; RANK; PENERAPAN TERHADAP PENCARIAN BASIS • Matriks mxn

VEKTOR BARIS

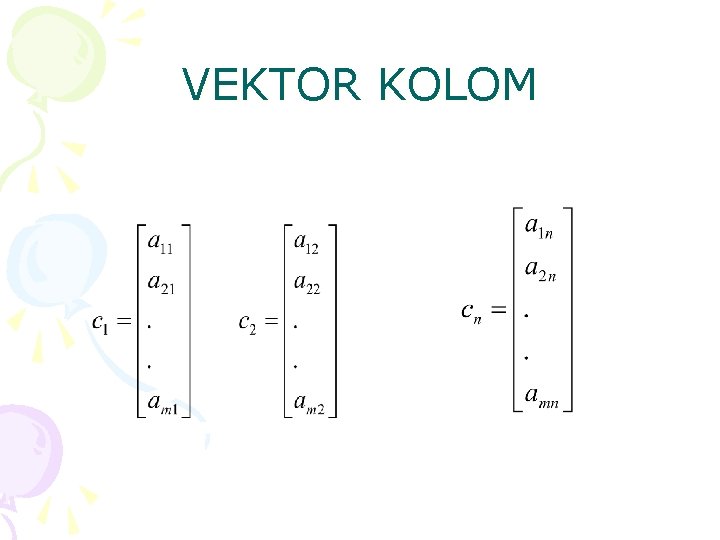
VEKTOR KOLOM

TEOREMA 12 - 14 • Operasi baris elementer tidak mengubah ruang baris sebuah matriks. • Vektor-vektor baris taknol berbentuk eselon baris dari matriks A membentuk basis untuk ruang baris A • Jika A adalah sebarang matriks, maka ruang baris dan ruang kolom A mempunyai dimensi yang sama. Dimensi ruang baris dan ruang kolom matriks A dinamakan rank A dan dinyatakan dengan rank (A).

TEOREMA 15 • Jika A adalah matriks n x n, maka pernyataan-pernyataan berikut ekivalen satu sama lain. – A dapat dibalik. – A x = 0 hanya mempunyai pemecahan trivial. – A ekivalen baris dengan In. – A x = b konsisten untuk tiap-tiap matriks b yang berukuran n x 1. – det(A) ≠ 0. – A mempunyai rank n. – Vektor-vektor baris A bebas linear. – Vektor-vektor kolom A bebas linear

TEOREMA 16 - 18 • Sebuah sistem persamaan linear Ax = b adalah konsisten jika dan hanya jika b berada pada ruang kolom A • Sebuah sistem persamaan linear Ax = b akan konsisten jika dan hanya jika rank dari matriks koefisien A sama dengan rank dari matriks yang diperbesar [A|b]. • Jika Ax = b adalah sistem linear konsisten dari m persamaan n bilangan takdiketahui, dan jika A mempunyai rank r, maka pemecahan sistem tersebut mengandung n – r parameter