Chapter 7 Transcendental Functions 1 7 1 Inverse
















































































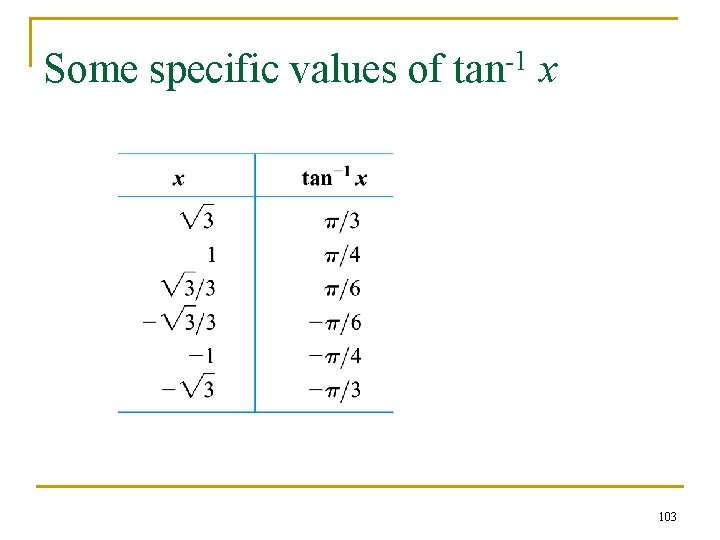




















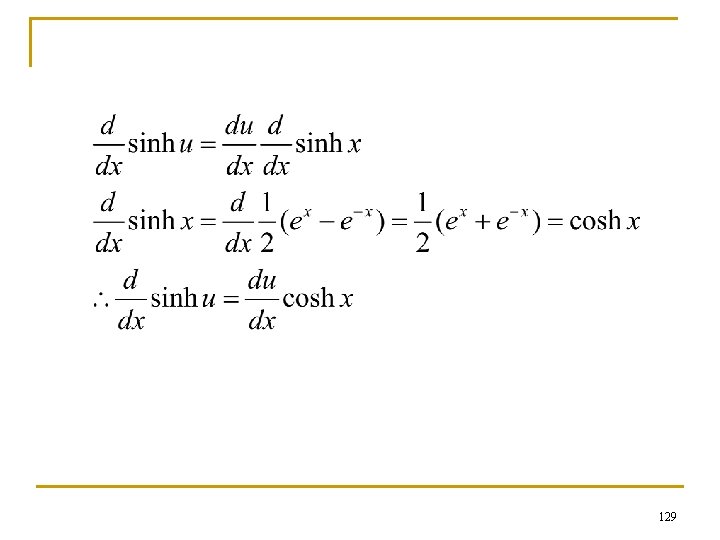










- Slides: 140

Chapter 7 Transcendental Functions 1

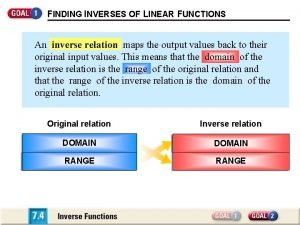
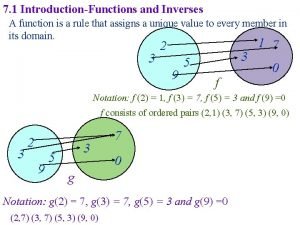
7. 1 Inverse Functions and Their Derivatives 2

3

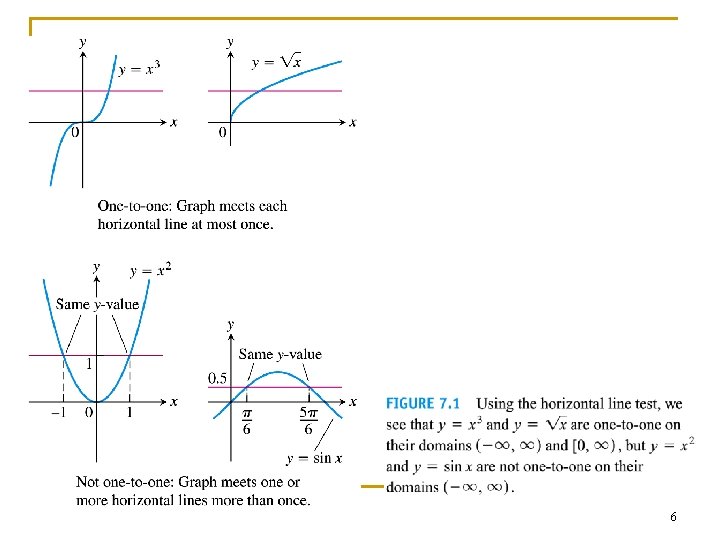
Example 1 Domains of one-to-one functions n n (a) f(x) = x 1/2 is one-to-one on any domain of nonnegative numbers (b) g(x) = sin x is NOT one-to-one on [0, p] but one-to-one on [0, p/2]. 4

5

6

7

8

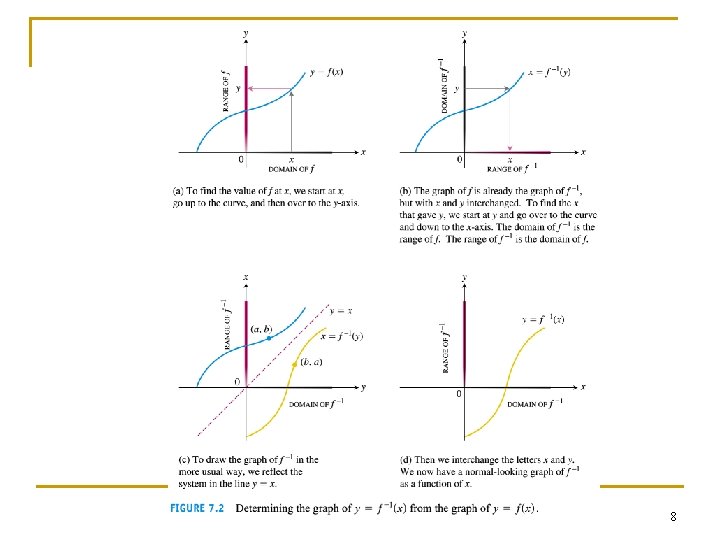
Finding inverses 1. Solve the equation y =f(x) for x. This gives a formula x = f -1(y) where x is expressed as a function of y. 2. Interchange x and y, obtaining a formula y = f -1(x) where f -1(x) is expressed in the conventional format with x as the independent variable and y as the dependent variables. n 9

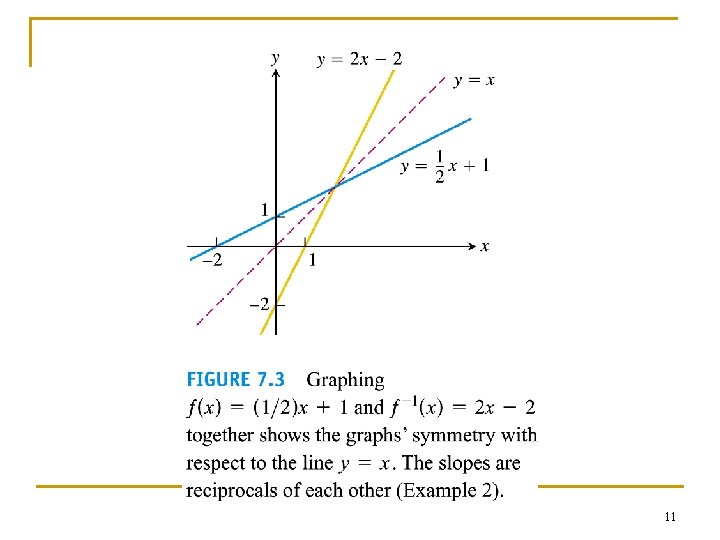
Example 2 Finding an inverse function n Find the inverse of y = x/2 + 1, expressed as a function of x. n Solution 1. solve for x in terms of y: x = 2(y – 1) 2. interchange x and y: y = 2(x – 1) The inverse function f-1(x) = 2(x – 1) Check: f -1[f(x)] = 2[f(x) – 1] = 2[(x/2 + 1) – 1] = x = f [f -1 (x)] n n 10

11

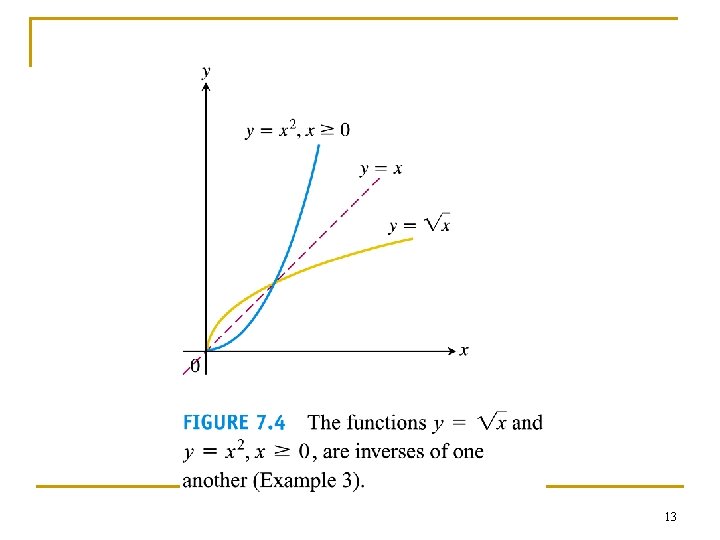
Example 3 Finding an inverse function n n Find the inverse of y = x 2, x ≥ 0, expressed as a function of x. Solution 1. solve for x in terms of y: x = y 2. interchange x and y: y = x The inverse function f-1(x) = x 12

13

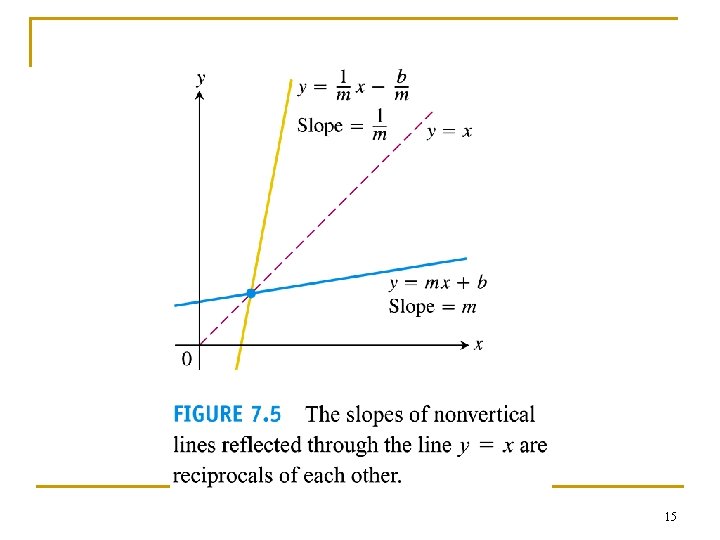
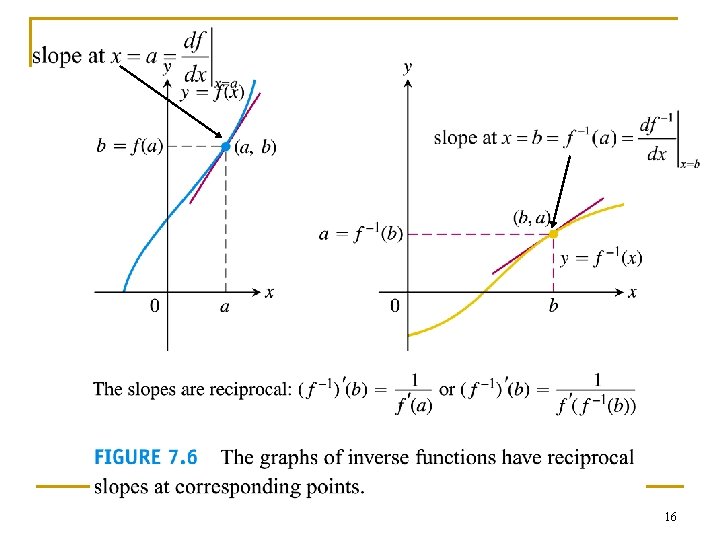
Derivatives of inverses of differentiable functions n n n From example 2 (a linear function) f(x) = x/2 + 1; f-1(x) = 2(x + 1); df(x)/dx = 1/2; df -1(x)/dx = 2, i. e. df(x)/dx = 1/df -1(x)/dx Such a result is obvious because their graphs are obtained by reflecting on the y = x line. In general, the reciprocal relationship between the slopes of f and f-1 holds for other functions. 14

15

16

17

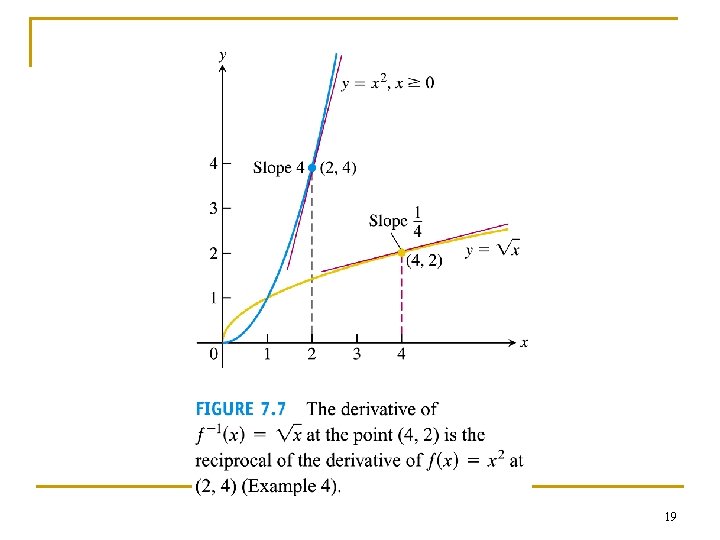
Example 4 Applying theorem 1 The function f(x) = x 2, x ≥ 0 and its inverse f 1(x) = x have derivatives f '(x) = 2 x, and (f -1)'(x) = 1/(2 x). n Theorem 1 predicts that the derivative of f -1(x) is (f -1)'(x) = 1/ f '[f -1(x)] = 1/ f '[ x] = 1/(2 x) n 18

19

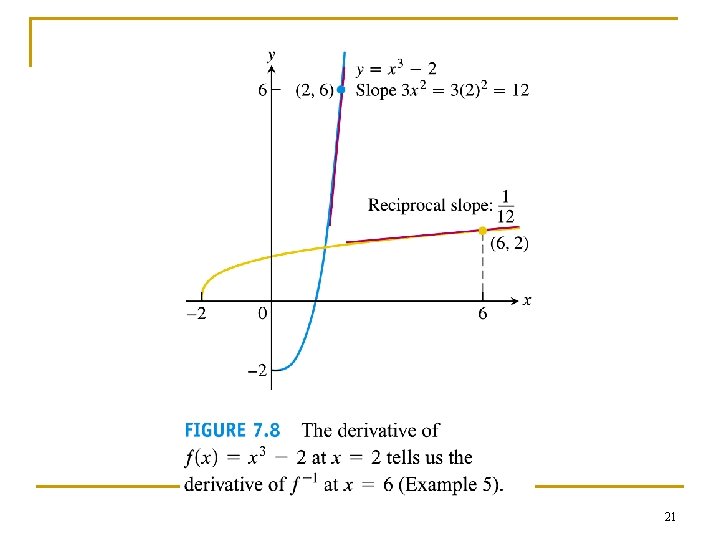
Example 5 Finding a value of the inverse derivative n n n Let f(x) = x 3 – 2. Find the value of df -1/dx at x = 6 = f(2) without a formula for f -1. The point for f is (2, 6); The corresponding point for f -1 is (6, 2). Solution df /dx =3 x 2 df -1/dx|x=6 = 1/(df /dx|x=2)= 1/(df/dx|x= 2) = 1/3 x 2|x=2 = 1/12 20

21

7. 2 Natural Logarithms 22

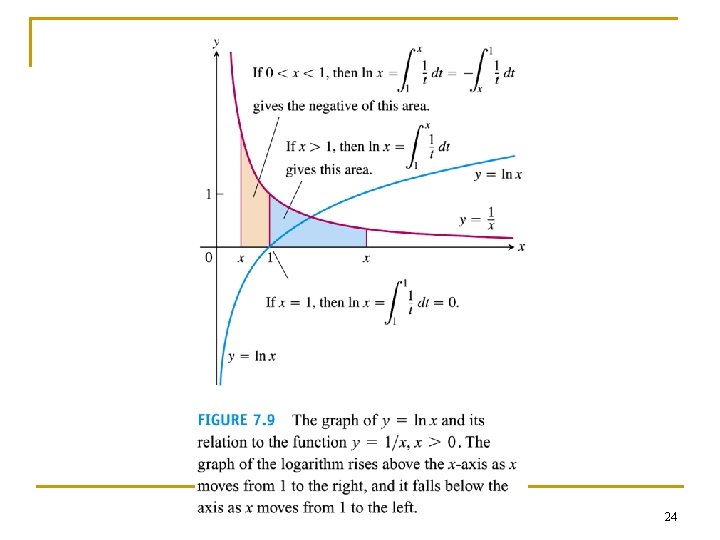
Definition of natural logarithmic fuction 23

24

n. Domain of ln x = (0, ∞) n. Range of ln x = (-∞, ∞) nln x is an increasing function since dy/dx = 1/x > 0 25

e lies between 2 and 3 ln x = 1 26

27

By definition, the antiderivative of ln x is just 1/x Let u = u (x). By chain rule, d/dx [ln u(x)] = d/du(ln u) du(x)/dx =(1/u) du(x)/dx 28

Example 1 Derivatives of natural logarithms 29

Properties of logarithms 30

Example 2 Interpreting the properties of logarithms 31

Example 3 Applying the properties to function formulas 32

Proof of ln ax = ln a + ln x n ln ax and ln x have the same derivative: n Hence, by the corollary 2 of the mean value theorem, they differs by a constant C n We will prove that C = ln a by applying the definition ln x at x = 1. 33

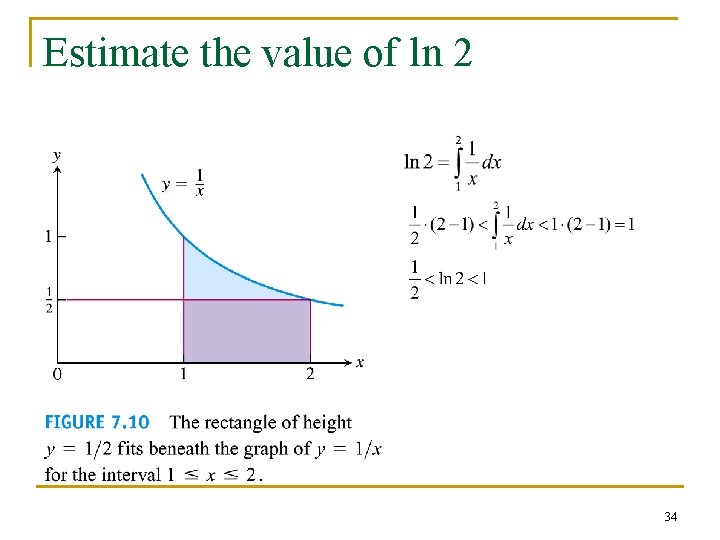
Estimate the value of ln 2 34

The integral (1/u) du 35

36

Example 4 Applying equation (5) 37

The integrals of tan x and cot x 38

Example 5 39

Example 6 Using logarithmic differentiation n Find dy/dx if 40

7. 3 The Exponential Function 41

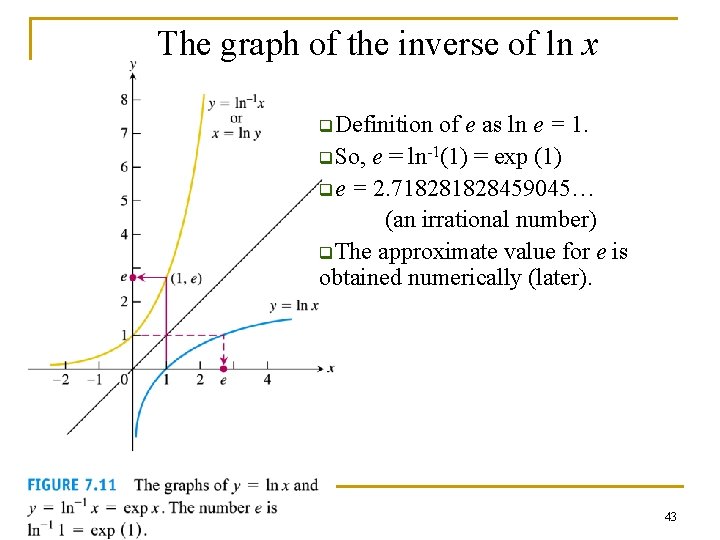
The inverse of ln x and the number e n ln x is one-to-one, hence it has an inverse. We name the inverse of ln x, ln-1 x as exp (x) 42

The graph of the inverse of ln x q. Definition of e as ln e = 1. q. So, e = ln-1(1) = exp (1) qe = 2. 71828459045… (an irrational number) q. The approximate value for e is obtained numerically (later). 43

The function y = ex n n We can raise the number e to a rational power r, er er is positive since e is positive, hence er has a logarithm (recall that logarithm is defied only for positive number). From the power rule of theorem 2 on the properties of natural logarithm, ln xr = r ln x, where r is rational, we have ln er = r We take the inverse to obtain ln-1 (ln er) = ln-1 (r) er = ln-1 (r) exp r, for r rational. 44

The number e to a real (possibly irrational) power x n n How do we define ex where x is irrational? This can be defined by assigning ex as exp x since ln-1 (x) is defined (as the inverse function of ln x is defined for all real x). 45

Note: please do make a distinction between ex and exp x. They have different definitions. ex is the number e raised to the power of real number x. exp x is defined as the inverse of the logarithmic function, exp x = ln-1 x 46

47

n n (2) follows from the definition of the exponent function: From ex = exp x, let x → ln x eln x = exp[ln x] = x (by definition). For (3): From ex = exp x, take logarithm both sides, → ln ex = ln [exp x] = x (by definition) 48

Example 1 Using inverse equations 49

Example 2 Solving for an exponent n Find k if e 2 k=10. 50

The general exponential function ax n n Since a = elna for any positive number a ax = (elna)x = exlna For the first time we have a precise meaning for an irrational exponent. (previously ax is defined for only rational x and a) 51

Example 3 Evaluating exponential functions 52

Laws of exponents Theorem 3 also valid for ax 53

Proof of law 1 54

Example 4 Applying the exponent laws 55

The derivative and integral of ex 56

Example 5 Differentiating an exponential 57

By the virtue of the chain rule, we obtain This is the integral equivalent of (6) 58

Example 7 Integrating exponentials 59

The number e expressed as a limit 60

Proof n If f(x) = ln x, then f '(x) = 1/x, so f '(1) = 1. But by definition of derivative, n 61

62

63

n By virtue of chain rule, 64

Example 9 using the power rule with irrational powers 65

7. 4 ax and loga x 66

The derivative of ax By virtue of the chain rule, 67

Example 1 Differentiating general exponential functions 68

Other power functions n n Example 2 Differentiating a general power function Find dy/dx if y = xx, x > 0. Solution: Write xx as a power of e xx = exlnx 69

Integral of u a 70

Example 3 Integrating general exponential functions 71

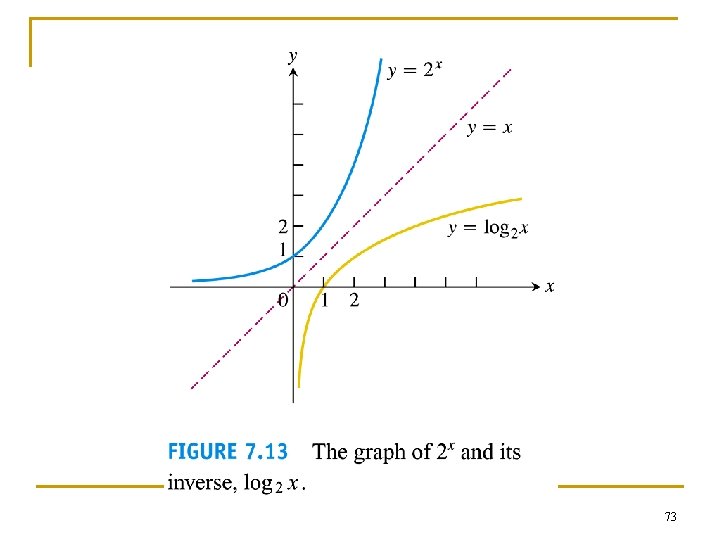
Logarithm with base a 72

73

Example 4 Applying the inverse equations 74

Evaluation of loga x n Example: log 102= ln 2/ ln 10 75

n Proof of rule 1: 76

Derivatives and integrals involving loga x 77

Example 5 78

7. 5 Exponential Growth and Decay 79

The law of exponential change n For a quantity y increases or decreases at a rate proportional to it size at a give time t follows the law of exponential change, as per 80

81

Example 1 Reducing the cases of infectious disease n Suppose that in the course of any given year the number of cases of a disease is reduced by 20%. If there are 10, 000 cases today, how many years will it take to reduce the number to 1000? Assume the law of exponential change applies. 82

Example 3 Half-life of a radioactive element n The effective radioactive lifetime of polonium 210 is very short (in days). The number of radioactive atoms remaining after t days in a sample that starts with y 0 radioactive atoms is y= y 0 exp(-5 10 -3 t). Find the element’s half life. 83

Solution Radioactive elements decay according to the exponential law of change. The half life of a given radioactive element can be expressed in term of the rate constant k that is specific to a given radioactive species. Here k=-5 10 -3. n At the half-life, t= t 1/2, y(t 1/2)= y 0/2 = y 0 exp(-5 10 -3 t 1/2) = 1/2 ln(1/2) = -5 10 -3 t 1/2 = - ln(1/2)/5 10 -3 = ln(2)/5 10 -3 = … n 84

7. 7 Inverse Trigonometric Functions 85

Defining the inverses n n Trigo functions are periodic, hence not one-to -one in their domains. If we restrict the trigonometric functions to intervals on which they are one-to-one, then we can define their inverses. 86

Domain restriction that makes the trigonometric functions oneto-one 87

Domain restriction that makes the trigonometric functions oneto-one 88

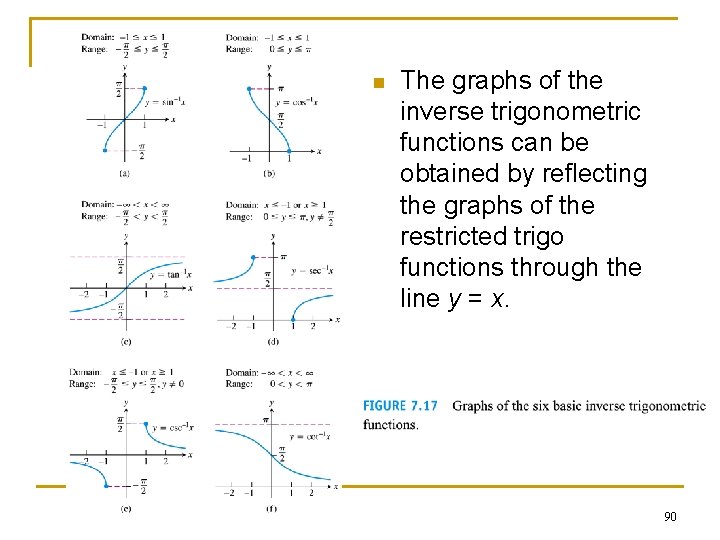
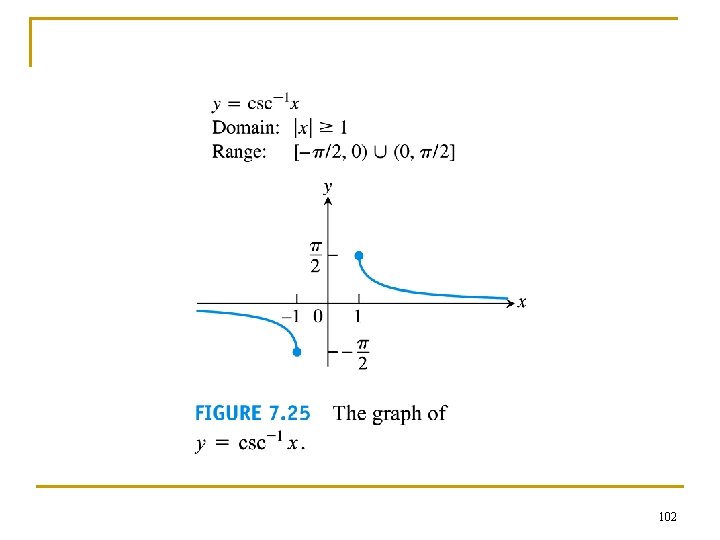
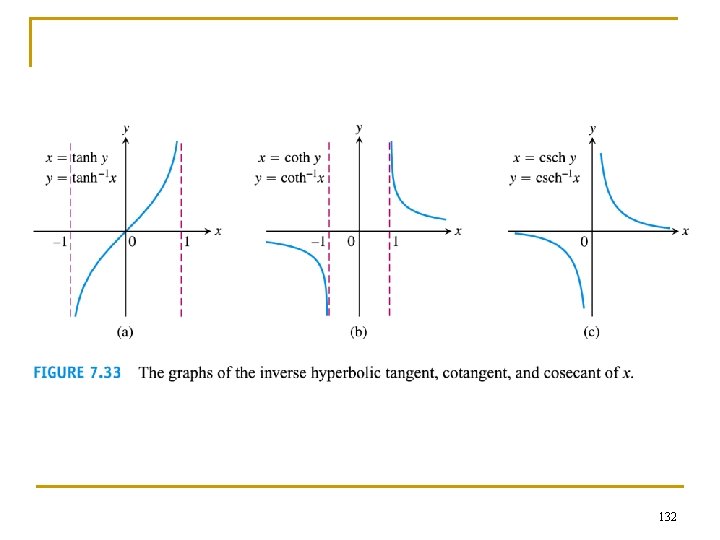
Inverses for the restricted trigo functions 89

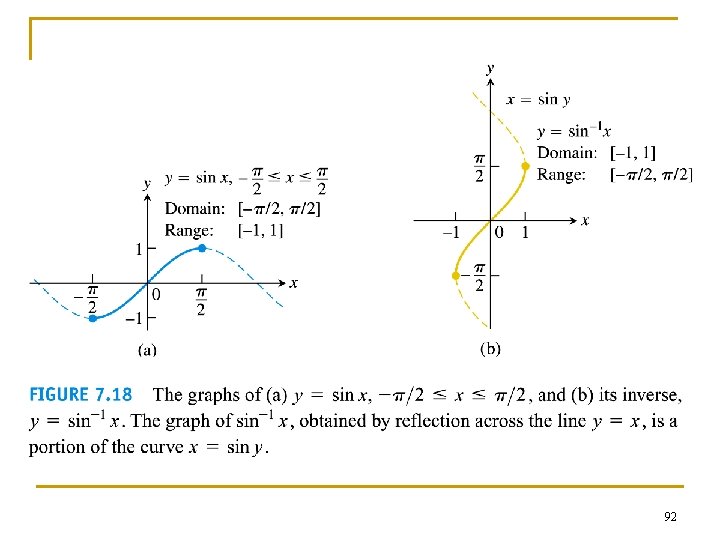
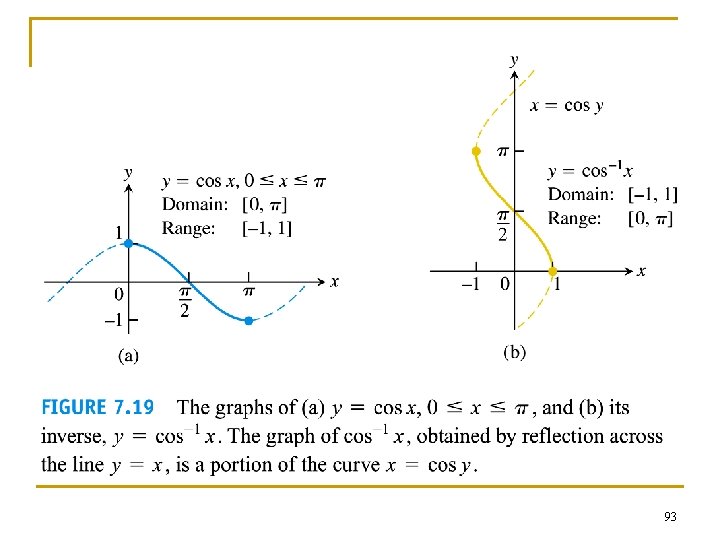
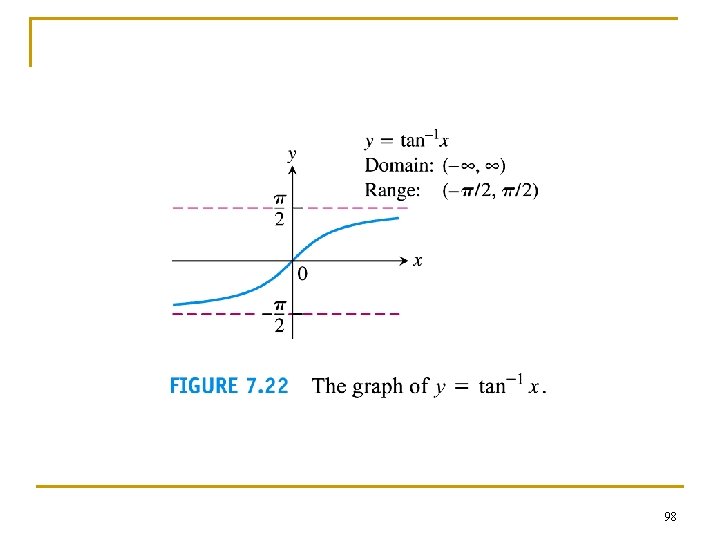
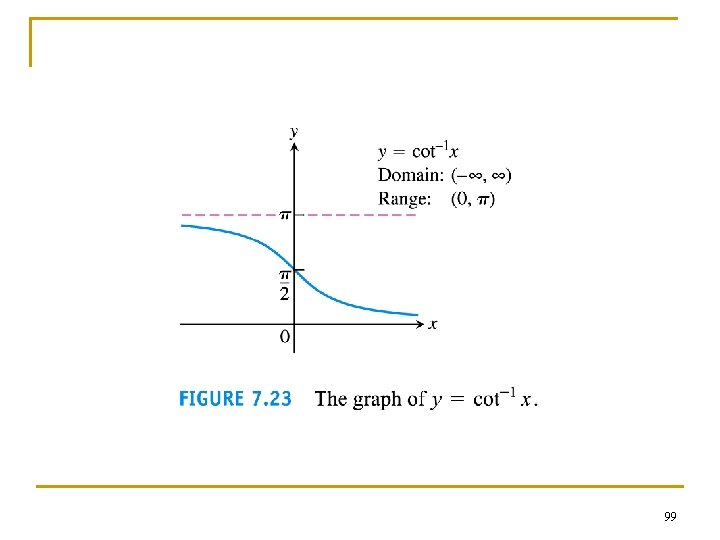
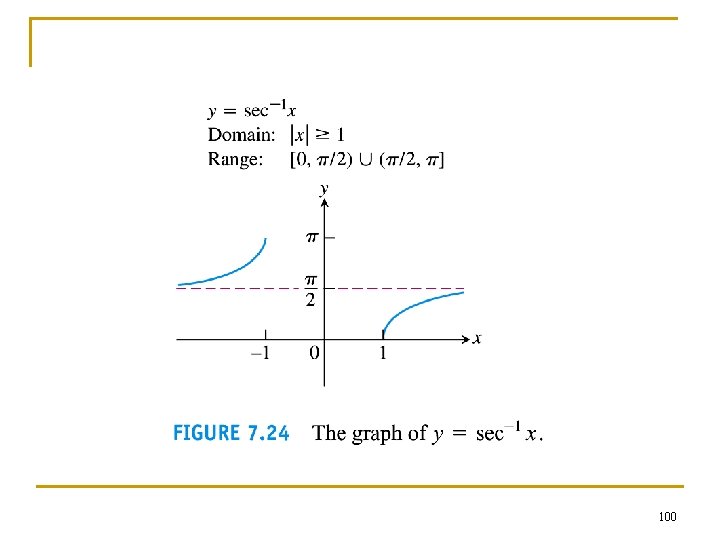
n The graphs of the inverse trigonometric functions can be obtained by reflecting the graphs of the restricted trigo functions through the line y = x. 90

91

92

93

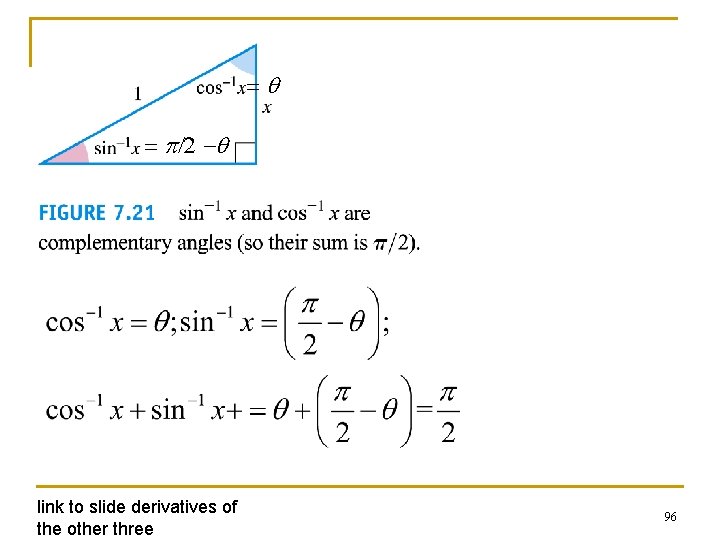
Some specific values of sin-1 x and cos-1 x 94

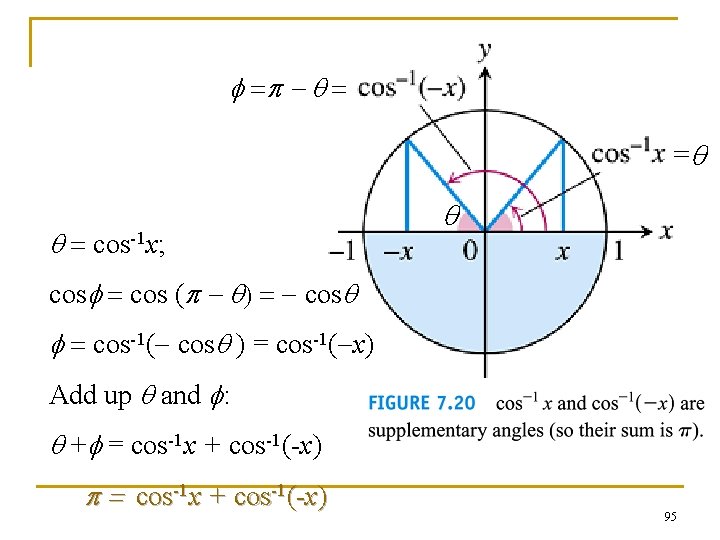
f =p - q = =q q = cos-1 x; q cosf = cos (p - q) = - cosq f = cos-1(- cosq ) = cos-1(-x) Add up q and f: q +f = cos-1 x + cos-1(-x) p = cos-1 x + cos-1(-x) 95

=q = p/2 -q link to slide derivatives of the other three 96

97

98

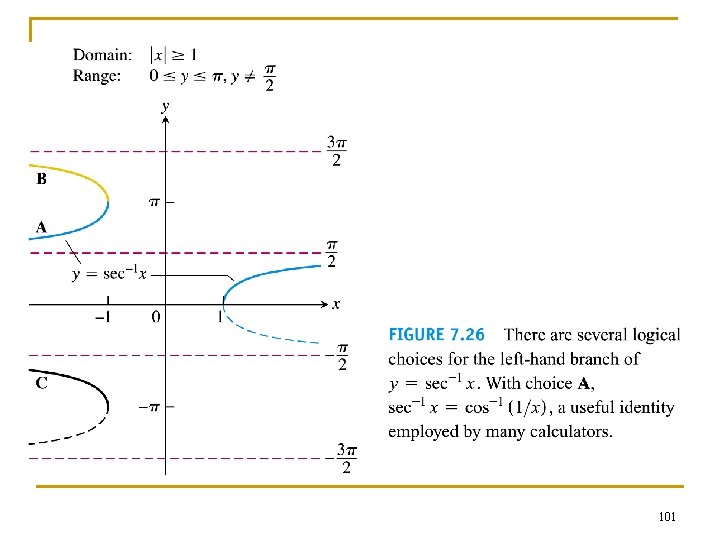
99

100

101

102
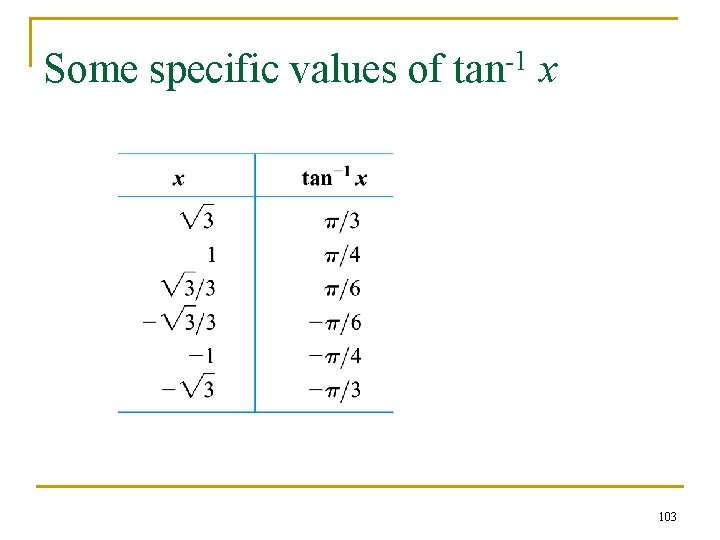
Some specific values of tan-1 x 103

Example 4 n Find cos a, tan a, sec a, csc a if a = sin-1 (2/3). n n sin a = 2/3. . . 104

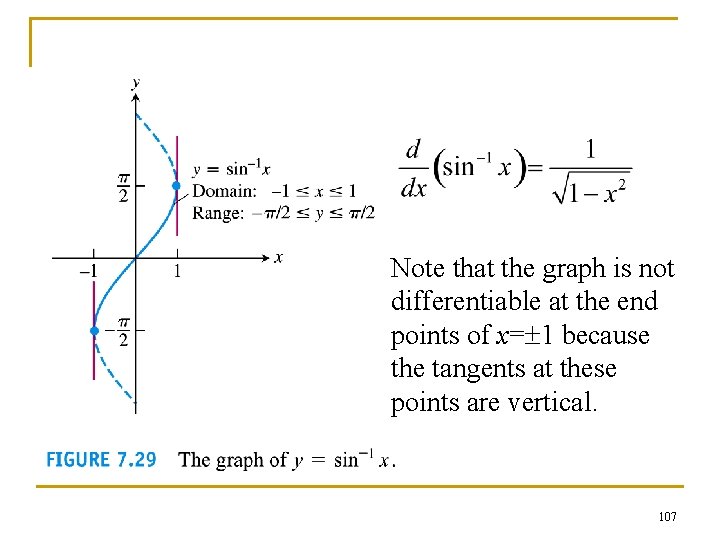
105

The derivative of y = sin-1 x 106

Note that the graph is not differentiable at the end points of x= 1 because the tangents at these points are vertical. 107

The derivative of y = -1 sin u Note that |u |<1 for the formula to apply 108

Example 7 Applying the derivative formula 109

The derivative of y = tan-1 u 1 x (1 -x 2) y By virtue of chain rule, we obtain 110

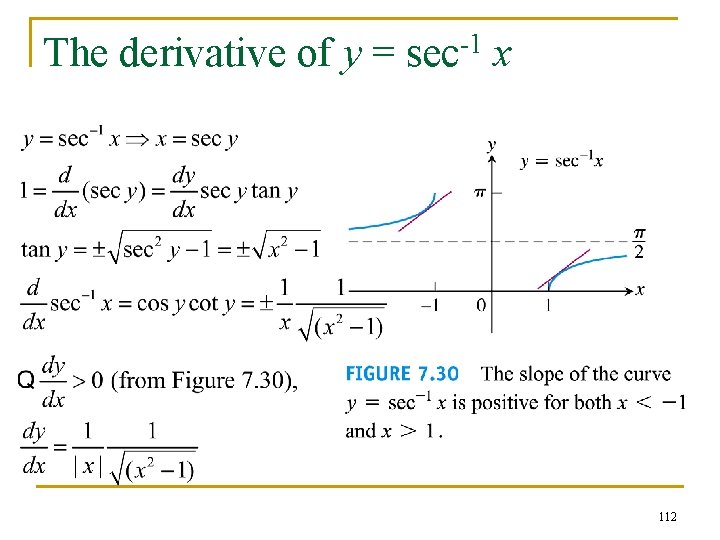
Example 8 111

The derivative of y = sec-1 x 112

The derivative of y = sec-1 u By virtue of chain rule, we obtain 113

Example 5 Using the formula 114

Derivatives of the other three n The derivative of cos-1 x, cot-1 x, csc-1 x can be easily obtained thanks to the following identities: Link to fig. 7. 21 115

116

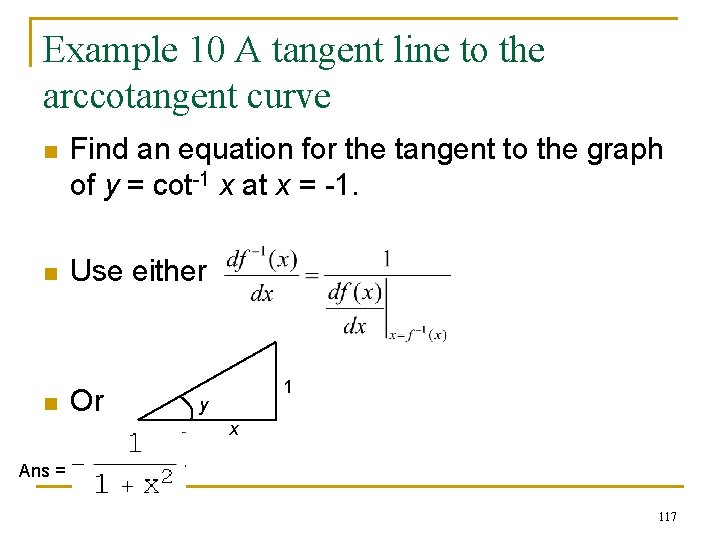
Example 10 A tangent line to the arccotangent curve n Find an equation for the tangent to the graph of y = cot-1 x at x = -1. n Use either n Or 1 y x Ans = 117

Integration formula n By integrating both sides of the derivative formulas in Table 7. 3, we obtain three useful integration formulas in Table 7. 4. 118

Example 11 Using the integral formulas 119

Example 13 Completing the square 120

Example 15 Using substitution 121

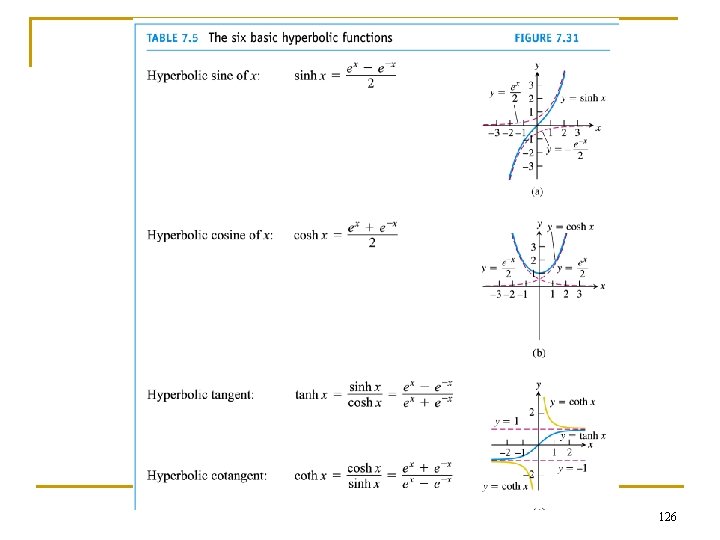
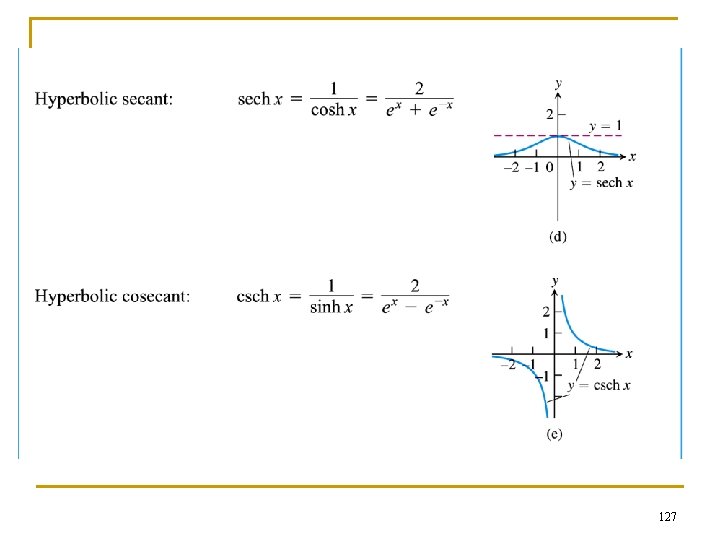
7. 8 Hyperbolic Functions 122

Even and odd parts of the exponential function n n n n In general: f (x) = ½ [f (x) + f (-x)] + ½ [f (x) - f (-x)] ½ [f (x) + f (-x)] is the even part ½ [f (x) - f (-x)] is the odd part Specifically: f (x) = ex = ½ (ex + e-x) + ½ (ex – e-x) The odd part ½ (ex - e-x) ≡ cosh x (hyperbolic cosine of x) The even part ½ (ex + e-x) ≡ sinh x (hyperbolic sine of x) 123

124

Proof of 125

126

127

Derivatives and integrals 128
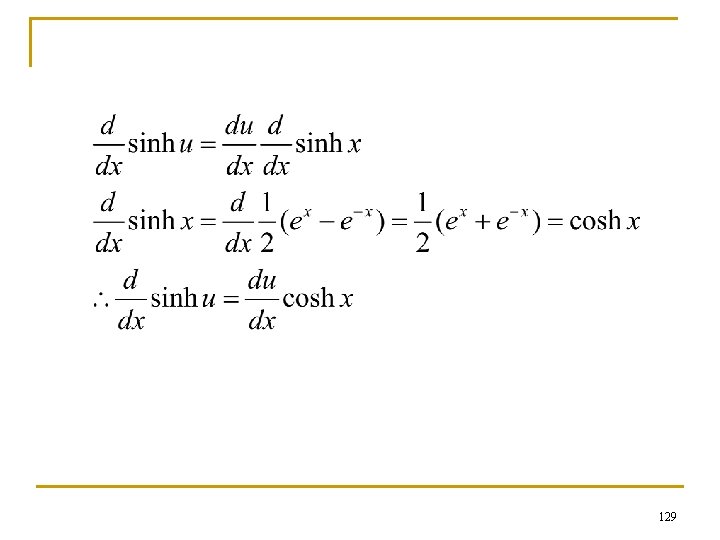
129

Example 1 Finding derivatives and integrals 130

Inverse hyperbolic functions The inverse is useful in integration. 131

132

Useful Identities 133

Proof 134

Integrating these formulas will allows us to obtain a list of useful integration formula involving hyperbolic functions 135

Proof 136

Example 2 Derivative of the inverse hyperbolic cosine n Show that 137

Example 3 Using table 7. 11 138

139

140
 Logarithmic exponential and other transcendental functions
Logarithmic exponential and other transcendental functions Transcendental functions
Transcendental functions Inverse function graph examples
Inverse function graph examples Logarithmic exponential and other transcendental functions
Logarithmic exponential and other transcendental functions Transcendentalism in english literature
Transcendentalism in english literature Rationalist vs empiricist
Rationalist vs empiricist Transcendental aesthetic
Transcendental aesthetic How transcendental are you
How transcendental are you Interpretive phenomenology
Interpretive phenomenology Transcendental movement
Transcendental movement Transcendental idealism
Transcendental idealism Transcendental self
Transcendental self Qualidade transcendental
Qualidade transcendental Conservation values and ethics
Conservation values and ethics Conservation ethics
Conservation ethics Find the exact value of . a. c. b. d.
Find the exact value of . a. c. b. d. Restrictions for inverse trig functions
Restrictions for inverse trig functions Properties of inverse trigonometric functions
Properties of inverse trigonometric functions Domain and range of tan function
Domain and range of tan function Kazkhistan
Kazkhistan 4-7 inverse linear functions
4-7 inverse linear functions Inverse of log
Inverse of log Simplify inverse trig functions
Simplify inverse trig functions Inverse function arrow diagram
Inverse function arrow diagram Derivatives of inverse functions and logarithms
Derivatives of inverse functions and logarithms Cos inverse x differentiation
Cos inverse x differentiation Integration of inverse trigonometric functions
Integration of inverse trigonometric functions Hyperbolic functions derivatives
Hyperbolic functions derivatives Inverse functions notes
Inverse functions notes Indeterminate forms
Indeterminate forms Inverse circular functions and trigonometric equations
Inverse circular functions and trigonometric equations Inverse variation graph calculator
Inverse variation graph calculator Integration of exponential
Integration of exponential Inverse relations and functions
Inverse relations and functions Inverse function in real life
Inverse function in real life Composition of inverse functions
Composition of inverse functions Lesson 1-4 inverses of functions
Lesson 1-4 inverses of functions Constant parent function graph
Constant parent function graph Implicit differentiation with inverse trig functions
Implicit differentiation with inverse trig functions Evaluating inverse trig functions without a calculator
Evaluating inverse trig functions without a calculator Inverse trig ratios and finding missing angles
Inverse trig ratios and finding missing angles Inverse laplace transform integral formula
Inverse laplace transform integral formula Proving inverse functions using composition
Proving inverse functions using composition Reverse exponential graph
Reverse exponential graph Inverse of a rational function
Inverse of a rational function 6-7 inverse relations and functions
6-7 inverse relations and functions 4-7 inverse linear functions
4-7 inverse linear functions Inverse relations and functions
Inverse relations and functions Inverse functions linear discrete
Inverse functions linear discrete Inverse of exponential functions
Inverse of exponential functions Inverse functions linear discrete
Inverse functions linear discrete Sin inverse formula
Sin inverse formula Inverse trig quadrants
Inverse trig quadrants Summary of inverse trigonometric functions
Summary of inverse trigonometric functions Tan inverse x differentiation
Tan inverse x differentiation Derivative of inverse sin
Derivative of inverse sin Inverse functions
Inverse functions Derivative of inverse trig functions
Derivative of inverse trig functions Absolute value piecewise function
Absolute value piecewise function How to evaluate function
How to evaluate function Evaluating functions and operations on functions
Evaluating functions and operations on functions Chapter 9 quadratic equations and functions
Chapter 9 quadratic equations and functions Chapter 8 quadratic functions and equations
Chapter 8 quadratic functions and equations Chapter 6 exponential and logarithmic functions answers
Chapter 6 exponential and logarithmic functions answers Chapter 4 polynomial and rational functions
Chapter 4 polynomial and rational functions Chapter 4 exponential and logarithmic functions
Chapter 4 exponential and logarithmic functions Chapter 4: exponential and logarithmic functions answer key
Chapter 4: exponential and logarithmic functions answer key Chapter 3 polynomial and rational functions
Chapter 3 polynomial and rational functions Chapter 11 structure and functions of the executive branch
Chapter 11 structure and functions of the executive branch Chapter 10 exponential and logarithmic functions answers
Chapter 10 exponential and logarithmic functions answers Chapter 10 exponential and logarithmic functions answers
Chapter 10 exponential and logarithmic functions answers Lesson 8 quadratic functions page 339
Lesson 8 quadratic functions page 339 Evaluating the six trigonometric functionsassignment
Evaluating the six trigonometric functionsassignment Unit 6 polynomials and polynomial functions
Unit 6 polynomials and polynomial functions Chapter 6 quadratic functions and inequalities answers
Chapter 6 quadratic functions and inequalities answers Chapter 4 trigonometric functions
Chapter 4 trigonometric functions Chapter 1 functions and their graphs
Chapter 1 functions and their graphs Chapter 6 trigonometry
Chapter 6 trigonometry Lesson 5-2
Lesson 5-2 Condensing logarithmic functions
Condensing logarithmic functions Chapter 3 linear and quadratic functions
Chapter 3 linear and quadratic functions Chapter 2 functions and graphs
Chapter 2 functions and graphs Chapter 11 school policies and their functions
Chapter 11 school policies and their functions Chapter 1 quadratic functions and factoring
Chapter 1 quadratic functions and factoring Chapter 9 exponential and logarithmic functions answer key
Chapter 9 exponential and logarithmic functions answer key Chapter 9 exponential and logarithmic functions answer key
Chapter 9 exponential and logarithmic functions answer key Chapter 5 trigonometric functions
Chapter 5 trigonometric functions Chapter 5 exponential and logarithmic functions answer key
Chapter 5 exponential and logarithmic functions answer key Chapter 4 trigonometric functions
Chapter 4 trigonometric functions Chapter 3 graphing linear functions answer key
Chapter 3 graphing linear functions answer key Chapter 2 functions and their graphs answers
Chapter 2 functions and their graphs answers Chapter 1 graphs functions and models answers
Chapter 1 graphs functions and models answers Chapter 13 trigonometric functions answers
Chapter 13 trigonometric functions answers Excel project 2
Excel project 2 Chapter 5 exponential and logarithmic functions
Chapter 5 exponential and logarithmic functions Chapter 3 polynomial and rational functions
Chapter 3 polynomial and rational functions Chapter 3 exponential and logarithmic functions
Chapter 3 exponential and logarithmic functions Chapter 2 functions and graphs
Chapter 2 functions and graphs Chapter 11 structure and functions of the executive branch
Chapter 11 structure and functions of the executive branch Direct proportionality formula
Direct proportionality formula Inverse of log function
Inverse of log function Fonction de dirac
Fonction de dirac Inverse of log function
Inverse of log function Additive inverse of 2
Additive inverse of 2 Domain and range of sin inverse x
Domain and range of sin inverse x Soh cah toa inverse
Soh cah toa inverse Tabel invers transformasi laplace
Tabel invers transformasi laplace Inverse laplace of complex roots
Inverse laplace of complex roots Inverse error discrete math
Inverse error discrete math Fourier transform
Fourier transform Fourier transform of dirac
Fourier transform of dirac Dividing matrices
Dividing matrices Stretch extended analogy
Stretch extended analogy Inverse stretch reflex
Inverse stretch reflex Pythagorean theorem with square roots
Pythagorean theorem with square roots Using inverse operations
Using inverse operations Domain requirements
Domain requirements Inverse requirements
Inverse requirements Reciprocal of parabola
Reciprocal of parabola Inverse trig table
Inverse trig table Domain and range of an inverse function
Domain and range of an inverse function Calcoli percentuali sopra e sotto cento
Calcoli percentuali sopra e sotto cento Inverse proportion
Inverse proportion Commutative associative identity
Commutative associative identity Inverse property of addition
Inverse property of addition Stretch reflex
Stretch reflex Eutectic phase diagram
Eutectic phase diagram Inverse voltage
Inverse voltage 11-1 inverse variation
11-1 inverse variation Forward and inverse fourier transform
Forward and inverse fourier transform Parallelepipedo formule
Parallelepipedo formule Find an inverse of 101 modulo 4620
Find an inverse of 101 modulo 4620 Sconto composto formule inverse
Sconto composto formule inverse Invertible modulo
Invertible modulo Fish symbol in maths
Fish symbol in maths Sentence with converse
Sentence with converse Lacet inverse
Lacet inverse Modular inverse
Modular inverse 7^11 mod 23
7^11 mod 23 Inverse laplace transform in matlab
Inverse laplace transform in matlab Inverse lorentz transformation
Inverse lorentz transformation