Inverse Laplace Transform Consider a given function Fs








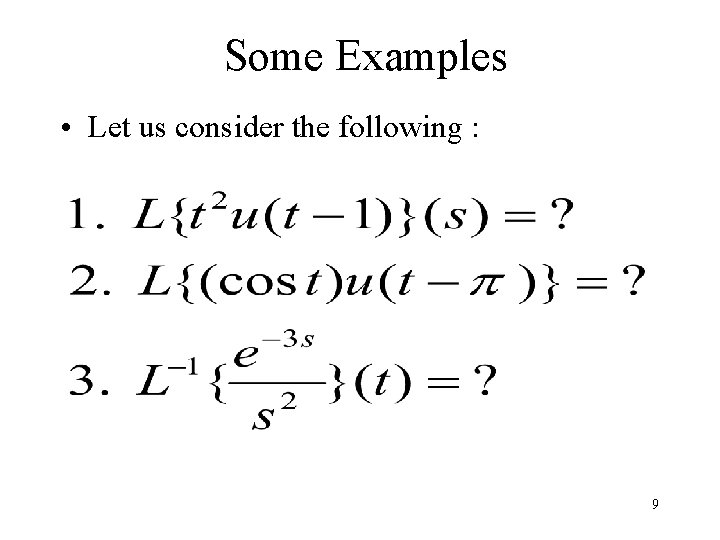






















- Slides: 31

Inverse Laplace Transform • Consider a given function F(s), is it possible to find a function f(t) defined on [0, ), such that • If this is possible, we say f(t) is the inverse Laplace transform of F(s), and we write 1

Some Examples. • First we note that the Inverse Laplace Transform is a “ Linear Operator”. 2

Applications • Consider the Initial Value Problem: • We shall use Laplace Transform and Inverse Laplace Transform to solve this I. V. P. 3

Next let us consider a D. E. with variable coefficents • Given the following I. V. P: (#36, P. 406) 4

Laplace Transform of Discontinuous and Periodic Functions • Discontinuous functions play a very important role in Engineering, for example: • This is known as the unit step function. 1 t 0 5

Shifts and scalar multiples of the Unit Step Functions 6

Unit step functions can be used to represent any piecewise continuous function. • For example: … • What is the Laplace Transform of u(t- a), a > 0? 7

Next, what is: 8
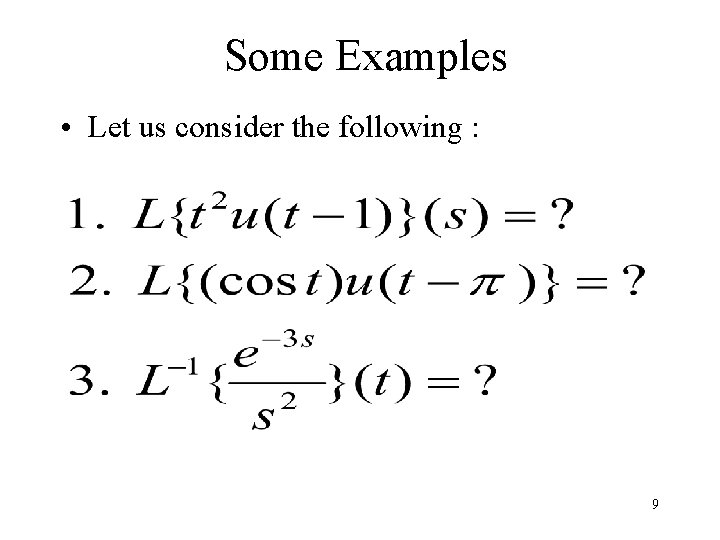
Some Examples • Let us consider the following : 9

Laplace Transform of Periodic Functions • Periodic functions play a very important role in the study of dynamical systems • Definition: A function f (t) is said to be periodic of period T, if for all t D(f) , we have f (t + T) = f (t). • For examples, sine waves, cosine waves and square waves are periodic functions. • What can we say about the transforms of periodic functions? 10

Let f T (t) be the part of f over the basic period [0, T]. This is known as the Windowed version of the periodic function f. • It is not difficult to see that f (t) can be written as the sum of translates of f T (t). Namely, 11

Example: The square wave with period 2 • Note that in this case f T (t) is given by : 1 1 2 t • f T (t) = 1 - u(t - 1). Hence 12

Some problems in the exercise • #10, 15, 31, 13

Convolution Operator “ * “. • Definition: Given two functions f (t) and g(t) piecewise continuous on [0, ). The convolution of f and g , denoted by • Covolution is 1. commutative, 2. distributive, 3. associative and with 4. existence of zero. 14

Laplace Transform of convolution • An important property of convolution is the • Theorem: 15

Proof of Convolution theorem can be done by • 1. Writing • 2. Then apply the Fubini’s theorem on interchanging the order of integration. 16

Applications • Solve the initial value problem 17

Example 2: Integral-Differential Equation • Consider the following equation: 18

Transfer function and Impulse response function • Consider the linear system governed by the I. V. P: • Thus given g(t) we wish to find the solution y(t). g(t) is called the input function and y(t) the output. The ratio of their Laplace Transforms, 19

For our example, take the Laplace transform of the I. V. P • we get • The inverse Laplace Transform of H(s), written h(t) = L-1{H(s)}(t) is called the Impulse response function for the system. Graph!! 20

This function h(t) is the unique solution to the homogeneous problem • Namely: • This can be checked easily (using Laplace transform). Now to solve a general I. V. P. such as • This is a non-homogeneous eq with non-trivial 21 initial values.

We shall split the given I. V. P into two problems • They are the equivalent to the original I. V. P. Namely: 22

Theorem on solution using Impulse Response Function • Theorem: Let I be an interval containing the origin. The unique solution to the initial value problem 23

Example • #24, P. 428 • Let a linear system be governed by the given initial value problem. • Find the transfer function H(s), the impulse response function h(t) and solve the I. V. P. • Recall: y(t) = (h*g)(t) + yk(t) 24

Dirac Delta Function • Paul A. M. Dirac, one of the great physicists from England invented the following function: • Definition: A function (t) having the following properties: • is called the Dirac delta function. It follows from (2) that for any function f(t) continuous in an open interval containing t = 0, we have 25

Remarks on Theory of Distribution. • Symbolic function, generalized function, and distribution function. 26

Heuristic argument on the existence of -function. • When a hammer strikes an object, it transfer momentum to the object. If the striking force is F(t) over a short time interval [t 0, t 1], then the total impulse due to F is the integral 27

This heuristic leads to conditions 1 and 2. 28

What is the Laplace Transform of -function? • By definition, we have 29

Application: • Consider the symbolic Initial Value Problem: 30

Linear Systems can be solved by Laplace Transform. (7. 9) • For two equations in two unknowns, steps are: • 1. Take the Laplace Transform of both equations in x(t) and y(t), • 2. Solve for X(s) and Y(s), then • 3. Take the inverse Laplace Transform of X(s) and Y(s), respectively. • 4. Work out some examples. 31
 Laplace transformtable
Laplace transformtable Inverse laplace transform of complex roots
Inverse laplace transform of complex roots Inverse laplace transform matlab
Inverse laplace transform matlab Convolution laplace transform
Convolution laplace transform Laplace transform
Laplace transform Inverse laplace transform
Inverse laplace transform Laplace of derivative
Laplace of derivative Laplace inverse formula
Laplace inverse formula Delta function fourier transform
Delta function fourier transform Fourier series of unit step function
Fourier series of unit step function Fourier
Fourier Augmented grammer
Augmented grammer Tranformasi z
Tranformasi z Initial value theorem
Initial value theorem Laplace transform of 1
Laplace transform of 1 Scott surgent asu
Scott surgent asu Differential laplace transform
Differential laplace transform Laplace transform of differential equation
Laplace transform of differential equation Laplace transform of impulse
Laplace transform of impulse What is s in laplace transform
What is s in laplace transform Initial value theorem of laplace transform
Initial value theorem of laplace transform Laplace of sint
Laplace of sint Laplace transform symbol
Laplace transform symbol Bilateral laplace transform table
Bilateral laplace transform table Heaviside method
Heaviside method Laplace table
Laplace table Differential laplace transform
Differential laplace transform Circuit analysis laplace transform
Circuit analysis laplace transform Z transform vs laplace
Z transform vs laplace Laplace transformation matlab
Laplace transformation matlab Relation between fourier and laplace transform
Relation between fourier and laplace transform Electric circuit analysis using laplace transform
Electric circuit analysis using laplace transform