Chapter 6 Polynomials and Polynomial Functions 6 1

Chapter 6 Polynomials and Polynomial Functions

6. 1 Using Properties of Exponents

Properties of Exponents Let a and b be real numbers and let m and n be integers. PRODUCT OF POWERS PROPERTY am • an = am+n POWER OF A POWER PROPERTY (am)n = amn POWER OF A PRODUCT PROPERTY (ab)m = ambm NEGATIVE EXPONENT PROPERTY ZERO EXPONENT PROPERTY QUOTIENT OF POWERS PROPERTY POWER OF A QUOTIENT PROPERTY a 0 = 1, a ≠ 0

A number is expressed in Scientific Notation if it is in the form c X 10 n where 1 ≤ c < 10 and n is an integer. Decimal to scientific Notation: 5, 284, 000 = 5. 284 X 106 0. 0000075 = 7. 5 X 10 -6 Scientific Notation to decimal: 3. 45670123 X 108 = 345, 670, 123 6. 546 X 10 -5 = 0. 00006546

Classwork: Pg 326 – 328 (1 -15, 48, 52, 53) Homework: Pg 326 – 328 (16 -46 every 3 rd, 47, 49 -51, 54 -56)

6. 2 Evaluating and Graphing Polynomial Functions

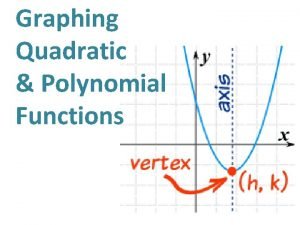
A Polynomial Function : Leading Coefficient: Constant Term: a 0 Degree: n Standard Form: terms are written in descending order of exponents from left to right

A Polynomial Function in Standard Form: Leading Coefficient: Constant Term: 5 Degree: 3 Standard Form: terms are written in descending order of exponents from left to right

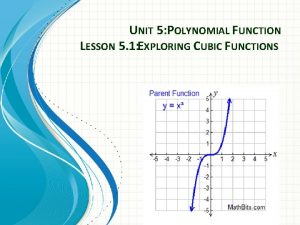
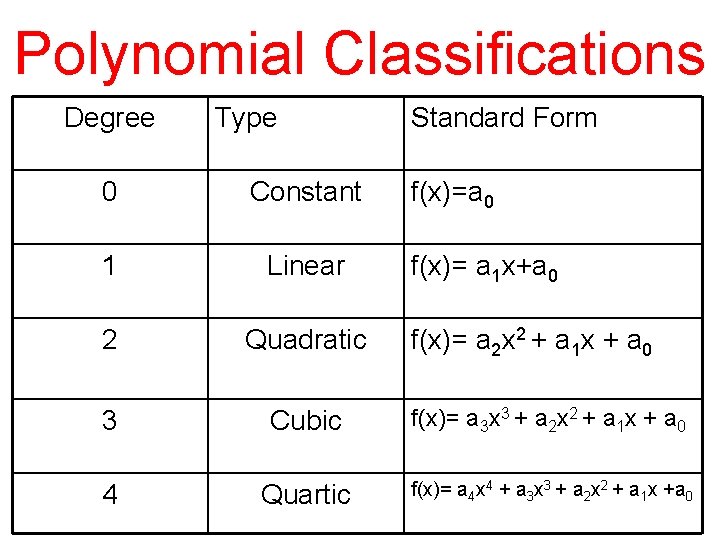
Polynomial Classifications Degree Type Standard Form 0 Constant f(x)=a 0 1 Linear 2 Quadratic 3 Cubic f(x)= a 3 x 3 + a 2 x 2 + a 1 x + a 0 4 Quartic f(x)= a 4 x 4 + a 3 x 3 + a 2 x 2 + a 1 x +a 0 f(x)= a 1 x+a 0 f(x)= a 2 x 2 + a 1 x + a 0

Synthetic Substitution Use synthetic Substitution to evaluate f(x)=2 x 4 - 8 x 2 + 5 x – 7 when x = 3. Write the value of x and the coefficients of ƒ(x) as shown. Polynomial in standard form 2 x 4 + 0 x 3 - 8 x 2 + 5 x – 7 2 0 -8 add 6 18 5 -7 30 105 35 98 3 3 Coefficients f(3) = 98 X x-value 2 6 10 The value of f(x) is the last number written in the bottom right hand corner

END BEHAVIOR FOR POLYNOMIAL FUNCTIONS For an>0 and n is even, both ends point up For an>0 and n is odd, left end points down and right end points up For an<0 and n is even, both ends point down For an<0 and n is odd, left end points up and right end points down See chart on pg 331

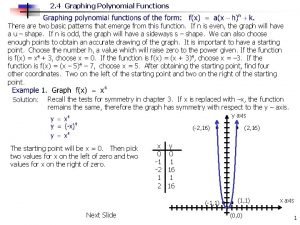
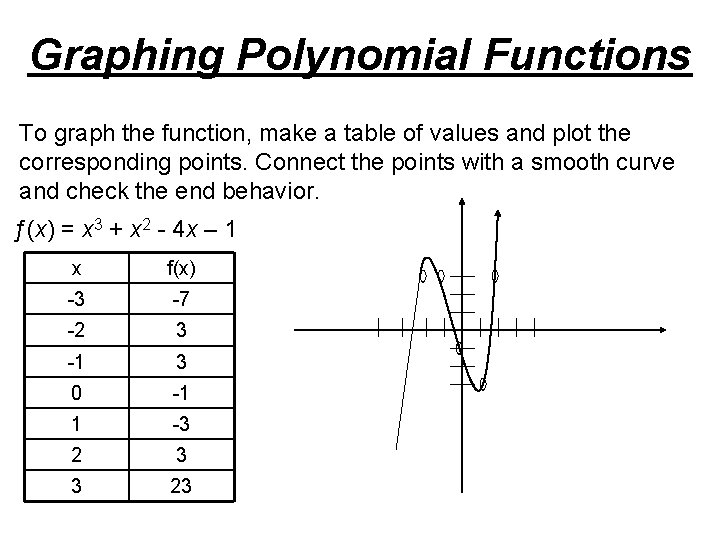
Graphing Polynomial Functions To graph the function, make a table of values and plot the corresponding points. Connect the points with a smooth curve and check the end behavior. ƒ(x) = x 3 + x 2 - 4 x – 1 x f(x) -3 -7 -2 3 -1 3 0 -1 1 -3 2 3 3 23

Classwork: Pg 333 – 336 (1 -13, 65, 68) Homework: Pg 333 – 336 (15, 16, 20, 21, 22, 25, 27, 28, 36, 37, 41, 45, 47, 4952, 53, 56, 59, 62, 66, 70, 81)

6. 3 Adding, Subtracting, and Multiplying Polynomials

To add or subtract polynomials, add or subtract the coefficients of like terms. You can use a vertical or horizontal format. 3 x 3+ 2 x 2 – x - 7 (9 x 3 - 2 x + 1) + (5 x 2 + 12 x - 4) = 9 x 3 + 5 x 2 - 2 x + 1 – 4 + x 3 - 10 x 2 - x + 8 = 9 x 3 + 5 x 2 + 10 x - 3 4 x 3 - 8 x 2 - x + 1 8 x 3 - 3 x 2 - 2 x + 9 -(2 x 3 + 6 x 2 -x + 1) -2 x 3 - 6 x 2 + x - 1 Add the opposite. 6 x 3 – 9 x 2 – x + 8 (2 x 2 + 3 x) -(3 x 2 + x - 4) = 2 x 2 + 3 x - 3 x 2 - x + 4 = - x 2 + 2 x + 4 Add the opposite.

Multiplying Polynomials To Multiply polynomials, use the distributive property regardless if you use the vertical or horizontal method. Horizontally Vertically (x - 3)(3 x 2 - 2 x - 4)=x(3 x 2)+x(-2 x)+x(-4)-3(3 x 2)-3(-2 x)-3(-4) =3 x 3 – 2 x 2 - 4 x – 9 x 2 + 6 x + 12 - x 2 + 2 x + 4 X =3 x 3 – 11 x 2 + 2 x +12 x-3 3 x 2 - 6 x - 12 Multiply -x 2 + 2 x + 4 by -3. -x 3 + 2 x 2 +4 x Multiply -x 2 + 2 x + 4 by x. -x + 5 x 2 – 2 x - 12 Combine like terms.

Special Product Patterns SUM AND DIFFERENCE (a + b)(a - b) = a 2 - b 2 Example (x + 3)(x - 3) = x 2 - 9 SQUARE OF A BINOMIAL (a + b)2 = a 2 + 2 ab + b 2 (y + 4)2 = y 2 + 8 y + 16 (a - b)2 = a 2 - 2 ab + b 2 (3 t 2 - 2)2 = 9 t 4 - 12 t 2 + 4 CUBE OF A BINOMIAL (a + b)3 = a 3 + 3 a 2 b + 3 ab 2 + b 3 (x + 1)3 = x 3 + 3 x 2 + 3 x + 1 (a - b)3 = a 3 - 3 a 2 b + 3 ab 2 - b 3 (p - 2)3 = p 3 - 6 p 2 + 12 p - 8

Classwork: Pg 341 – 343 (1 -12) Homework: Pg 341 – 343 (13 – 60 every 3 rd, 62, 63)

6. 4 Factoring and Solving Polynomial Equations

In Chapter 5 you learned how to factor the following types of quadratic expressions. TYPE EXAMPLE General trinomial 2 x 2 - 5 x - 12 = (2 x + 3)(x - 4) Perfect square trinomial x 2 + 10 x + 25 = (x + 5)2 Difference of two squares 4 x 2 - 9 = (2 x + 3)(2 x - 3) Common monomial factor 6 x 2 + 15 x = 3 x(2 x + 5) In this lesson you will learn how to factor other types of polynomials.

SPECIAL FACTORING PATTERNS SUM OF TWO CUBES Example a 3 + b 3 = (a + b)(a 2 - ab + b 2) x 3 + 8 = (x + 2)(x 2 - 2 x + 4) DIFFERENCE OF TWO CUBES a 3 - b 3 = (a - b)(a 2 + ab + b 2) x 3 + 27 = x 3 + 33 8 x 3 - 1 = (2 x - 1)(4 x 2 + 2 x + 1) Sum of two cubes = (x + 3)(x 2 - 3 x + 9) 16 u 5 - 250 u 2 = 2 u 2(8 u 3 - 125) = 2 u 2[(2 u)3 – 53] = 2 u 2(2 u - 5)(4 u 2 + 10 u + 25) Factor common monomial. Difference of two cubes

Factor By Grouping The pattern for this is as follows. ra + rb + sa + sb = r(a + b) + s(a + b) = (r + s)(a + b) x 3 - 2 x 2 - 9 x + 18 = x 2(x - 2) - 9(x - 2) Factor by grouping. = (x 2 - 9)(x - 2) = (x + 3)(x - 2) Difference of squares

In Chapter 5 you learned how to use the zero product property to solve factorable quadratic equations. You can extend this technique to solve some higher-degree polynomial equations. Solve 2 x 5 + 24 x = 14 x 3 Write original equation. 2 x 5 - 14 x 3 + 24 x = 0 Rewrite in standard form. 2 x(x 4 - 7 x 2 + 12) = 0 Factor common monomial. 2 x(x 2 - 3)(x 2 - 4) = 0 Factor trinomial. 2 x(x 2 - 3)(x + 2)(x - 2) = 0 Factor difference of squares. x = 0, x = Zero product property , x=- The solutions are 0, , x = -2, or x = 2 , , -2, and 2. Check these in the original equation.

Classwork: Pg 348 – 350 (1 -3, 5 -16, 88) Homework: Pg 348 – 350 (18, 21, 24, 2732, 33, 37, 41, 45, 49, 50, 51, 68, 71, 77, 80, 89)

6. 5 The Remainder and Factor Theorems If a polynomial ƒ(x) is divided by x -k, then the remainder is r = ƒ(k). REMAINDER THEOREM A polynomial ƒ(x) has a factor x - k if and only if ƒ(k) = 0. FACTOR THEOREM

Polynomial Long Division Divide 2 x 4 + 3 x 3 + 5 x - 1 by x 2 - 2 x + 2. Subtract 2 x 2(x 2 - 2 x+2) Subtract 7 x(x 2 - 2 x+2) Subtract 10(x 2 - 2 x+2) Remainder Answer

Synthetic Division Divide x 3 + 2 x 2 - 6 x - 9 by x - 2 Solve for x: x-2=0 2 1 X=2 1 2 -6 -9 2 8 4 4 2 -5 When writing solution, reduce the degree of the polynomial by 1. Add the remainder divided by the divisor at the end of the answer Answer

If the remainder is 0 then the divisor is a solution or a zero or a factor. You can use this fact to help factor completely.

Classwork: Pg 356 -358 (4 -13, 39, 47) Homework: P 356 – 358 (15 -54 every 3 rd)