CHAPTER 4 Polynomial and Rational Functions 4 1

  • Slides: 25
Download presentation

CHAPTER 4: Polynomial and Rational Functions 4. 1 Polynomial Functions and Models 4. 2

CHAPTER 4: Polynomial and Rational Functions 4. 1 Polynomial Functions and Models 4. 2 Graphing Polynomial Functions 4. 3 Polynomial Division; The Remainder and Factor Theorems 4. 4 Theorems about Zeros of Polynomial Functions 4. 5 Rational Functions 4. 6 Polynomial and Rational Inequalities Copyright © 2009 Pearson Education, Inc.

4. 5 Rational Functions · For a rational function, find the domain and graph

4. 5 Rational Functions · For a rational function, find the domain and graph the function, identifying all of the asymptotes. · Solve applied problems involving rational functions. Copyright © 2009 Pearson Education, Inc.

Rational Function A rational function is a function f that is a quotient of

Rational Function A rational function is a function f that is a quotient of two polynomials, that is, where p(x) and q(x) are polynomials and where q(x) is not the zero polynomial. The domain of f consists of all inputs x for which q(x) 0. Copyright © 2009 Pearson Education, Inc. Slide 4. 5 -4

Example Consider . Find the domain and graph f. The graph of the function

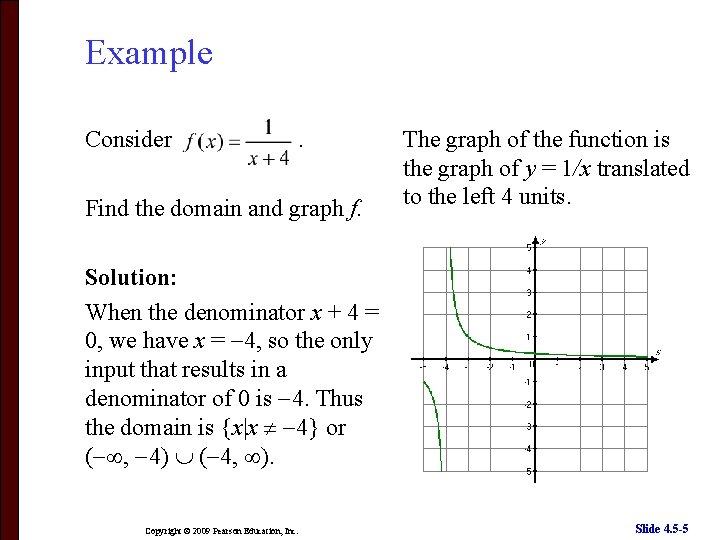
Example Consider . Find the domain and graph f. The graph of the function is the graph of y = 1/x translated to the left 4 units. Solution: When the denominator x + 4 = 0, we have x = 4, so the only input that results in a denominator of 0 is 4. Thus the domain is {x|x 4} or ( , 4) ( 4, ). Copyright © 2009 Pearson Education, Inc. Slide 4. 5 -5

Vertical Asymptotes The vertical asymptotes of a rational function f(x) = p(x)/q(x) are found

Vertical Asymptotes The vertical asymptotes of a rational function f(x) = p(x)/q(x) are found by determining the zeros of q(x) that are not also zeros of p(x). If p(x) and q(x) are polynomials with no common factors other than constants, we need to determine only the zeros of the denominator q(x). If a is a zero of the denominator but not the numerator, then the line x = a is a vertical asymptote for the graph of the function. Copyright © 2009 Pearson Education, Inc. Slide 4. 5 -6

Example Determine the vertical asymptotes of the function. Factor to find the zeros of

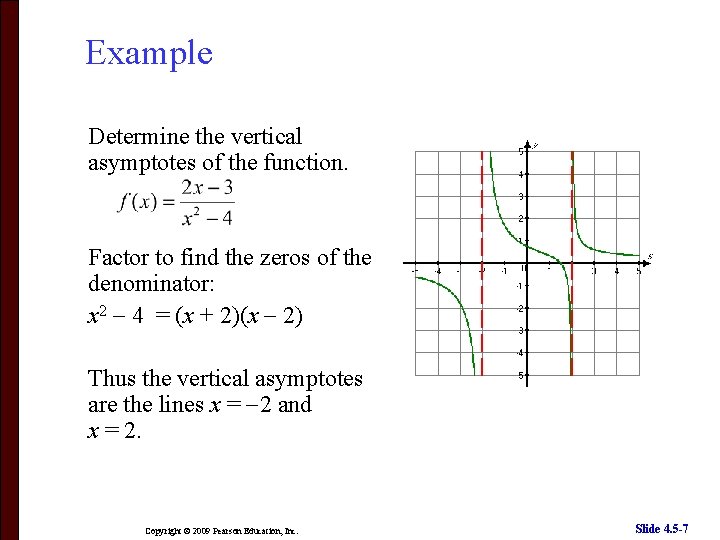
Example Determine the vertical asymptotes of the function. Factor to find the zeros of the denominator: x 2 4 = (x + 2)(x 2) Thus the vertical asymptotes are the lines x = 2 and x = 2. Copyright © 2009 Pearson Education, Inc. Slide 4. 5 -7

Horizontal Asymptote The line y = b is a horizontal asymptote for the graph

Horizontal Asymptote The line y = b is a horizontal asymptote for the graph of f if either or both of the following are true: When the numerator and the denominator of a rational function have the same degree, the line y = a/b is the horizontal asymptote, where a and b are the leading coefficients of the numerator and the denominator, respectively. Copyright © 2009 Pearson Education, Inc. Slide 4. 5 -8

Horizontal Asymptote Example: Find the horizontal asymptote: The numerator and denominator have the same

Horizontal Asymptote Example: Find the horizontal asymptote: The numerator and denominator have the same degree. The ratio of the leading coefficients is 6/9, so the line y = 2/3 is the horizontal asymptote. Copyright © 2009 Pearson Education, Inc. Slide 4. 5 -9

Determining a Horizontal Asymptote • • • When the numerator and the denominator of

Determining a Horizontal Asymptote • • • When the numerator and the denominator of a rational function have the same degree, the line y = a/b is the horizontal asymptote, where a and b are the leading coefficients of the numerator and the denominator, respectively. When the degree of the numerator of a rational function is less than the degree of the denominator, the x-axis, or y = 0, is the horizontal asymptote. When the degree of the numerator of a rational function is greater than the degree of the denominator, there is no horizontal asymptote. Copyright © 2009 Pearson Education, Inc. Slide 4. 5 -10

True Statements • The graph of a rational function never crosses a vertical asymptote.

True Statements • The graph of a rational function never crosses a vertical asymptote. • The graph of a rational function might cross a horizontal asymptote but does not necessarily do so. Copyright © 2009 Pearson Education, Inc. Slide 4. 5 -11

Example Graph Vertical asymptotes: x + 3 = 0, so x = 3. The

Example Graph Vertical asymptotes: x + 3 = 0, so x = 3. The degree of the numerator and denominator is the same. Thus y = 2, is the horizontal asymptote. 1. Draw the asymptotes with dashed lines. 2. Compute and plot some ordered pairs and draw the curve. Copyright © 2009 Pearson Education, Inc. Slide 4. 5 -12

Example continued x 7 5 4 2 0 2 h(x) 3. 5 5 8

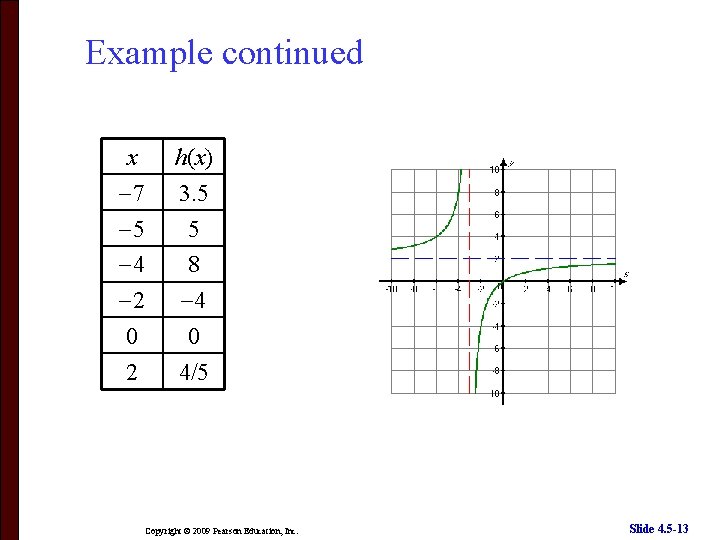
Example continued x 7 5 4 2 0 2 h(x) 3. 5 5 8 4 0 4/5 Copyright © 2009 Pearson Education, Inc. Slide 4. 5 -13

Oblique or Slant Asymptote Find all the asymptotes of . The line x =

Oblique or Slant Asymptote Find all the asymptotes of . The line x = 2 is a vertical asymptote. There is no horizontal asymptote because the degree of the numerator is greater than the degree of the denominator. Note that Copyright © 2009 Pearson Education, Inc. Slide 4. 5 -14

Oblique or Slant Asymptote continued Divide to find an equivalent expression. Copyright © 2009

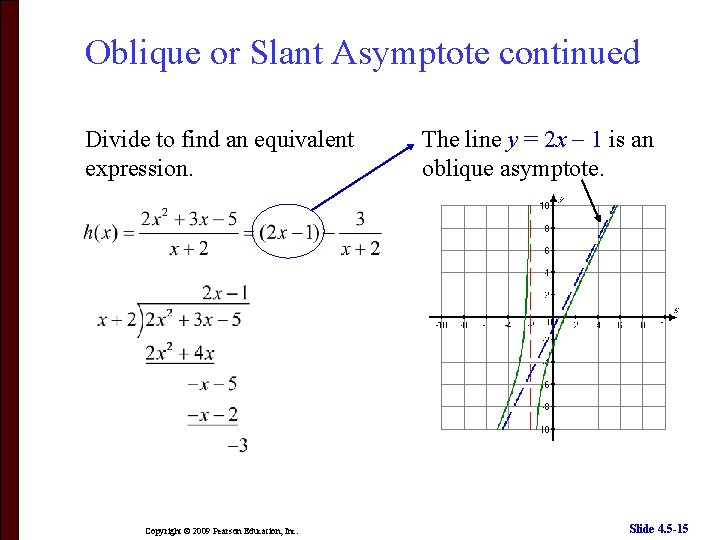
Oblique or Slant Asymptote continued Divide to find an equivalent expression. Copyright © 2009 Pearson Education, Inc. The line y = 2 x 1 is an oblique asymptote. Slide 4. 5 -15

Occurrence of Lines as Asymptotes of Rational Functions • • • For a rational

Occurrence of Lines as Asymptotes of Rational Functions • • • For a rational function f(x) = p(x)/q(x), where p(x) and q(x) have no common factors other than constants: Vertical asymptotes occur at any x-values that make the denominator 0. The x-axis is the horizontal asymptote when the degree of the numerator is less than the degree of the denominator. A horizontal asymptote other than the x-axis occurs when the numerator and the denominator have the same degree. Copyright © 2009 Pearson Education, Inc. Slide 4. 5 -16

Occurrence of Lines as Asymptotes of Rational Functions continued • • • An oblique

Occurrence of Lines as Asymptotes of Rational Functions continued • • • An oblique asymptote occurs when the degree of the numerator is 1 greater than the degree of the denominator. There can be only one horizontal asymptote or one oblique asymptote and never both. An asymptote is not part of the graph of the function. Copyright © 2009 Pearson Education, Inc. Slide 4. 5 -17

Graphing Rational Functions 1. Find the real zeros of the denominator. Determine the domain

Graphing Rational Functions 1. Find the real zeros of the denominator. Determine the domain of the function and sketch any vertical asymptotes. 2. Find the horizontal or oblique asymptote, if there is one, and sketch it. 3. Find the zeros of the function. The zeros are found by determining the zeros of the numerator. These are the first coordinates of the x-intercepts of the graph. 4. Find f (0). This gives the y-intercept (0, f (0)), of the function. 5. Find other function values to determine the general shape. Then draw the graph. Copyright © 2009 Pearson Education, Inc. Slide 4. 5 -18

Example Graph 1. Find the zeros by solving: The zeros are 1/2 and 3,

Example Graph 1. Find the zeros by solving: The zeros are 1/2 and 3, thus the domain excludes these values. The graph has vertical asymptotes at x = 3 and x = 1/2. We sketch these with dashed lines. 2. Because the degree of the numerator is less than the degree of the denominator, the x-axis, y = 0, is the horizontal asymptote. Copyright © 2009 Pearson Education, Inc. Slide 4. 5 -19

Example continued 3. To find the zeros of the numerator, we solve x +

Example continued 3. To find the zeros of the numerator, we solve x + 3 = 0 and get x = 3. Thus, 3 is the zero of the function, and the pair ( 3, 0) is the x-intercept. 4. We find f(0): Thus (0, 1) is the y-intercept. Copyright © 2009 Pearson Education, Inc. Slide 4. 5 -20

Example continued 5. We find other function values to determine the general shape of

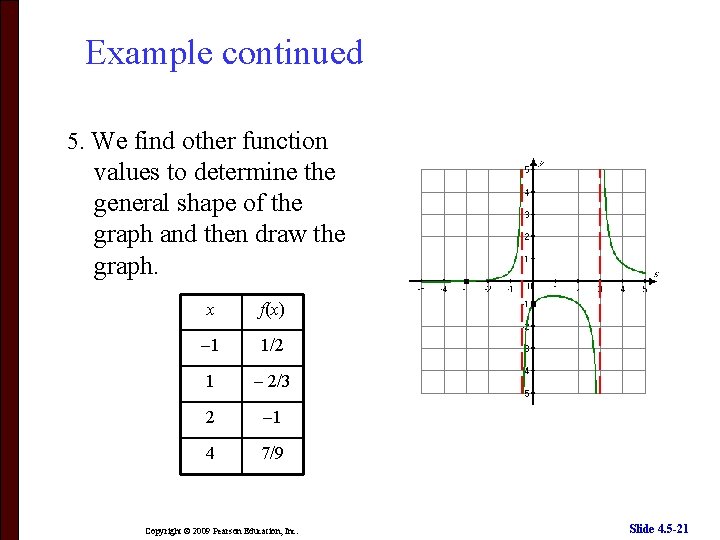
Example continued 5. We find other function values to determine the general shape of the graph and then draw the graph. x f(x) 1 1/2 1 2/3 2 1 4 7/9 Copyright © 2009 Pearson Education, Inc. Slide 4. 5 -21

More Examples Graph the following functions. a) b) c) Copyright © 2009 Pearson Education,

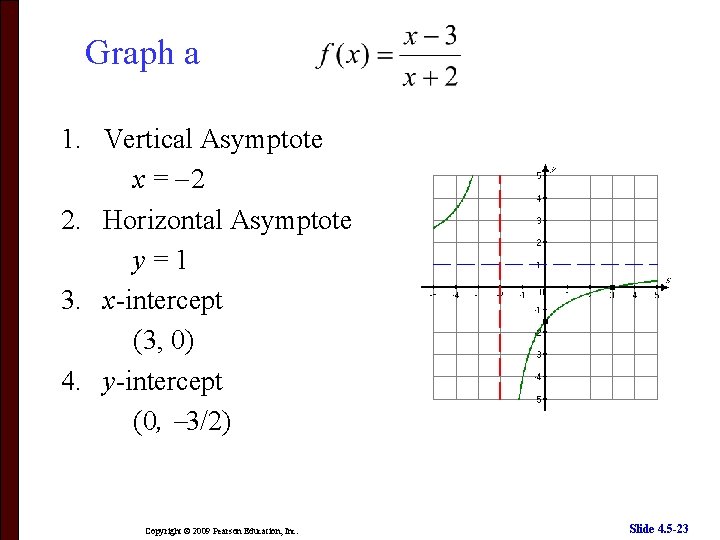
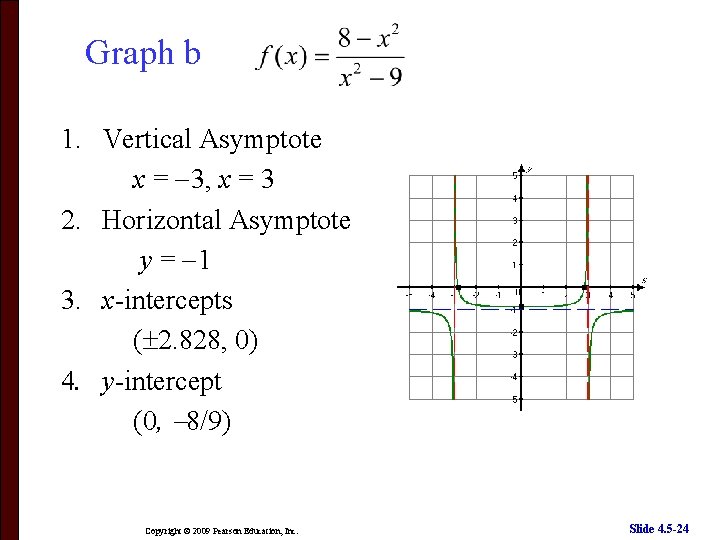
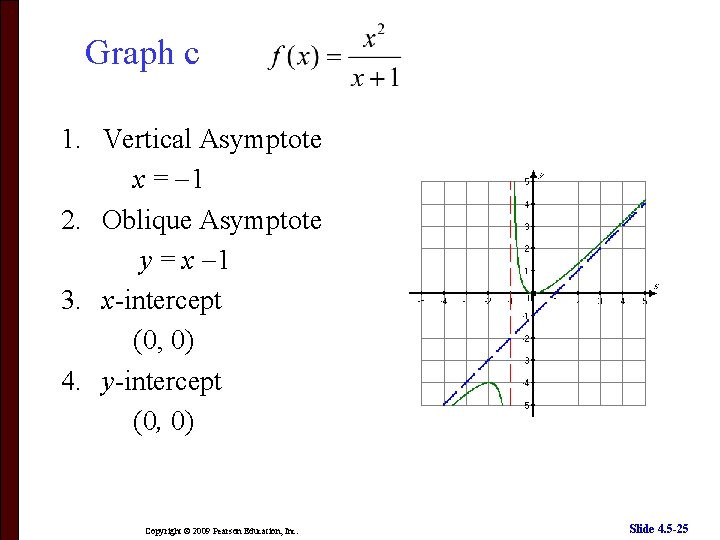
More Examples Graph the following functions. a) b) c) Copyright © 2009 Pearson Education, Inc. Slide 4. 5 -22

Graph a 1. Vertical Asymptote x = 2 2. Horizontal Asymptote y=1 3. x-intercept

Graph a 1. Vertical Asymptote x = 2 2. Horizontal Asymptote y=1 3. x-intercept (3, 0) 4. y-intercept (0, 3/2) Copyright © 2009 Pearson Education, Inc. Slide 4. 5 -23

Graph b 1. Vertical Asymptote x = 3, x = 3 2. Horizontal Asymptote

Graph b 1. Vertical Asymptote x = 3, x = 3 2. Horizontal Asymptote y = 1 3. x-intercepts ( 2. 828, 0) 4. y-intercept (0, 8/9) Copyright © 2009 Pearson Education, Inc. Slide 4. 5 -24

Graph c 1. Vertical Asymptote x = 1 2. Oblique Asymptote y = x

Graph c 1. Vertical Asymptote x = 1 2. Oblique Asymptote y = x 1 3. x-intercept (0, 0) 4. y-intercept (0, 0) Copyright © 2009 Pearson Education, Inc. Slide 4. 5 -25

5 3 Polynomial Functions Polynomial functions A polynomial5 3 Polynomial Functions Polynomial functions A polynomial
5 3 Polynomial Functions Polynomial Functions Polynomial Expression5 3 Polynomial Functions Polynomial Functions Polynomial Expression
Polynomial Functions EVALUATING POLYNOMIAL FUNCTIONS A polynomial functionPolynomial Functions EVALUATING POLYNOMIAL FUNCTIONS A polynomial function
Rational Functions I Rational functions A Rational functionRational Functions I Rational functions A Rational function
3 6 Rational Functions Rational Functions A rational3 6 Rational Functions Rational Functions A rational
3 6 Rational Functions Rational Functions A rational3 6 Rational Functions Rational Functions A rational
Chapter 4 Polynomial Rational Functions 4 4 RationalChapter 4 Polynomial Rational Functions 4 4 Rational
Rational Expressions Simplifying Rational Expressions Rational Expressions RationalRational Expressions Simplifying Rational Expressions Rational Expressions Rational
Chapter 8 Polynomial Functions and Rational Functions ALWAYSChapter 8 Polynomial Functions and Rational Functions ALWAYS
Chapter 8 Polynomial Functions and Rational Functions ALWAYSChapter 8 Polynomial Functions and Rational Functions ALWAYS
Chapter 4 Polynomial Functions and Rational Functions CopyrightChapter 4 Polynomial Functions and Rational Functions Copyright
Polynomial Functions and Their Graphs POLYNOMIAL FUNCTIONS APolynomial Functions and Their Graphs POLYNOMIAL FUNCTIONS A
Polynomial Functions and Graphs Higher Degree Polynomial FunctionsPolynomial Functions and Graphs Higher Degree Polynomial Functions
2 2 Polynomial Functions OBJECTIVE GRAPH POLYNOMIAL FUNCTIONS2 2 Polynomial Functions OBJECTIVE GRAPH POLYNOMIAL FUNCTIONS
Polynomial Functions Polynomial Functions An equation having aPolynomial Functions Polynomial Functions An equation having a
Graphing Polynomial Functions Graphs of Polynomial Functions 1Graphing Polynomial Functions Graphs of Polynomial Functions 1
Section 6 1 Polynomial Functions Exploring Polynomial FunctionsSection 6 1 Polynomial Functions Exploring Polynomial Functions
Polynomial Division Dividing one polynomial by another polynomialPolynomial Division Dividing one polynomial by another polynomial
YMBOIKO polynomial Expression Variable polynomial X X polynomialYMBOIKO polynomial Expression Variable polynomial X X polynomial
YMBOIKO polynomial Expression Variable polynomial X X polynomialYMBOIKO polynomial Expression Variable polynomial X X polynomial
YMBOIKO polynomial Expression Variable polynomial X X polynomialYMBOIKO polynomial Expression Variable polynomial X X polynomial
Polynomial Classes 1 class Polynomial public Polynomial PolynomialconstPolynomial Classes 1 class Polynomial public Polynomial Polynomialconst
Powerpoint Jeopardy Quadratic Polynomial Functions Models Rational FunctionsPowerpoint Jeopardy Quadratic Polynomial Functions Models Rational Functions
RATIONAL FUNCTIONS Model and graph rational functions YouRATIONAL FUNCTIONS Model and graph rational functions You