Polynomial Functions and Their Graphs POLYNOMIAL FUNCTIONS A
















- Slides: 28

Polynomial Functions and Their Graphs

POLYNOMIAL FUNCTIONS A POLYNOMIAL is a monomial or a sum of monomials. A POLYNOMIAL IN ONE VARIABLE is a polynomial that contains only one variable. Example: 5 x 2 + 3 x - 7

POLYNOMIAL FUNCTIONS The DEGREE of a polynomial in one variable is the greatest exponent of its variable. A LEADING COEFFICIENT is the coefficient of the term with the highest degree. What is the degree and leading coefficient of 3 x 5 – 3 x + 2 ?

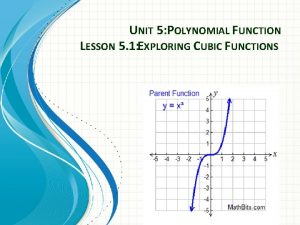
POLYNOMIAL FUNCTIONS A polynomial equation used to represent a function is called a POLYNOMIAL FUNCTION. Polynomial functions with a degree of 1 are called LINEAR POLYNOMIAL FUNCTIONS Polynomial functions with a degree of 2 are called QUADRATIC POLYNOMIAL FUNCTIONS Polynomial functions with a degree of 3 are called CUBIC POLYNOMIAL FUNCTIONS

POLYNOMIAL FUNCTIONS A polynomial function is an equation of the form f (x) = anxn + an-1 xn-1 + …+ a 2 x 2 + a 1 x + a 0 Where the coefficients an, an-1, ……a 1, a 0 is not zero, and the exponents are non-negative integers.

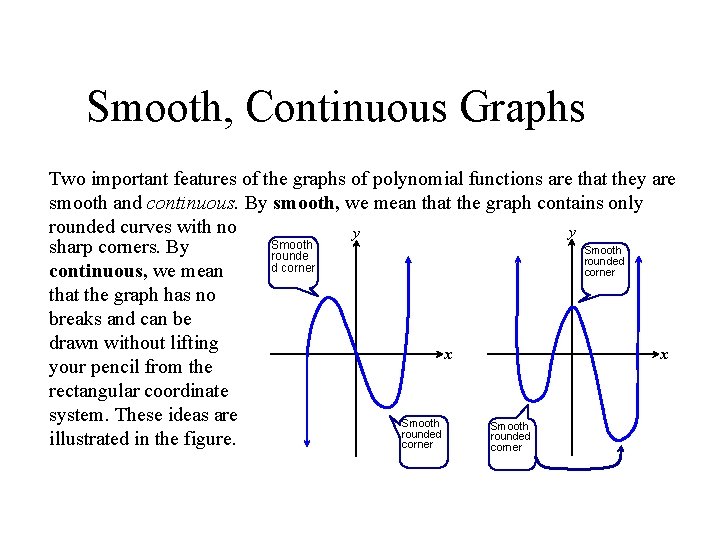
Smooth, Continuous Graphs Two important features of the graphs of polynomial functions are that they are smooth and continuous. By smooth, we mean that the graph contains only rounded curves with no y y Smooth sharp corners. By Smooth rounded d corner continuous, we mean that the graph has no breaks and can be drawn without lifting x x your pencil from the rectangular coordinate system. These ideas are Smooth rounded illustrated in the figure. corner

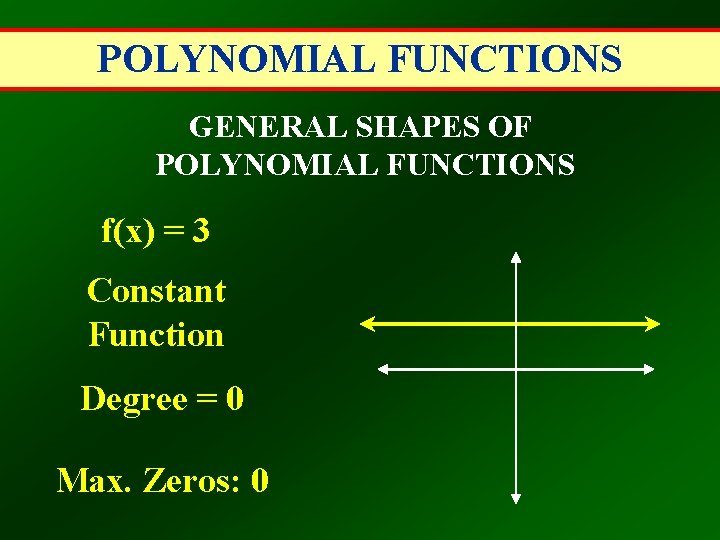
POLYNOMIAL FUNCTIONS GENERAL SHAPES OF POLYNOMIAL FUNCTIONS f(x) = 3 Constant Function Degree = 0 Max. Zeros: 0

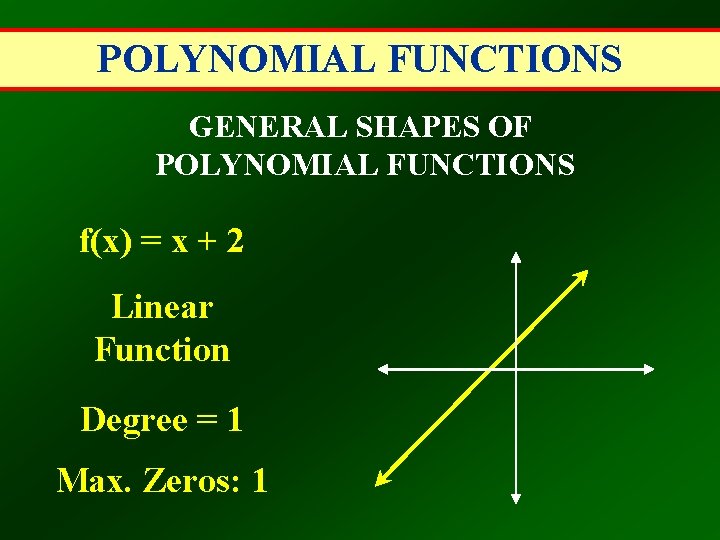
POLYNOMIAL FUNCTIONS GENERAL SHAPES OF POLYNOMIAL FUNCTIONS f(x) = x + 2 Linear Function Degree = 1 Max. Zeros: 1

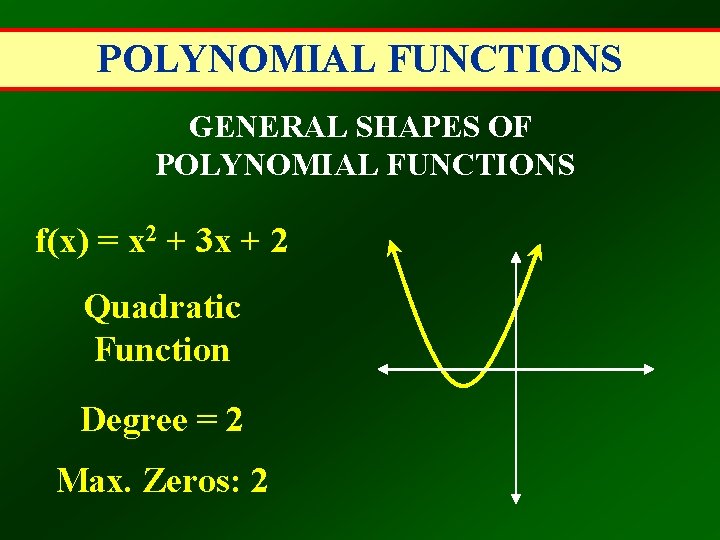
POLYNOMIAL FUNCTIONS GENERAL SHAPES OF POLYNOMIAL FUNCTIONS f(x) = x 2 + 3 x + 2 Quadratic Function Degree = 2 Max. Zeros: 2

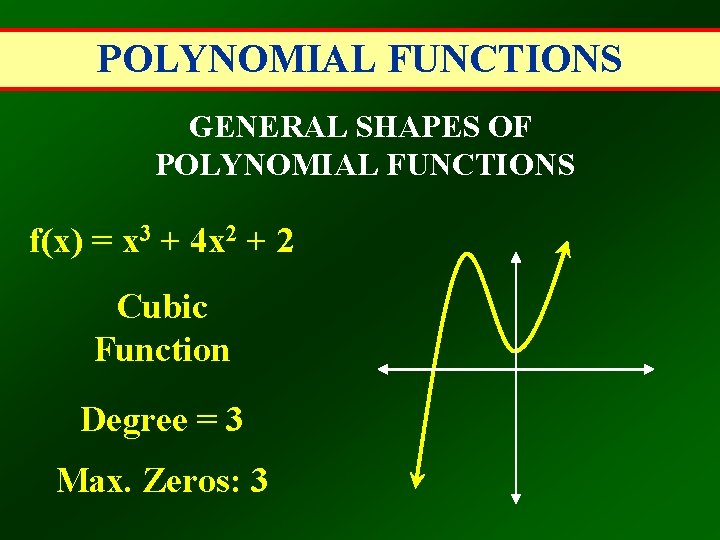
POLYNOMIAL FUNCTIONS GENERAL SHAPES OF POLYNOMIAL FUNCTIONS f(x) = x 3 + 4 x 2 + 2 Cubic Function Degree = 3 Max. Zeros: 3

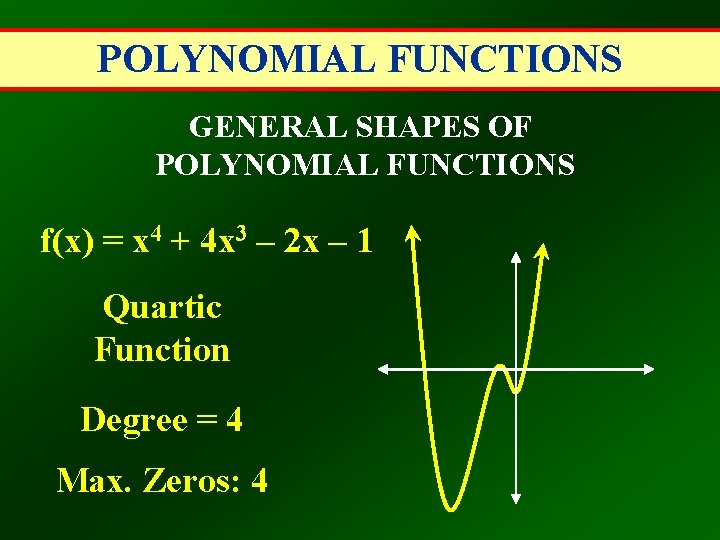
POLYNOMIAL FUNCTIONS GENERAL SHAPES OF POLYNOMIAL FUNCTIONS f(x) = x 4 + 4 x 3 – 2 x – 1 Quartic Function Degree = 4 Max. Zeros: 4

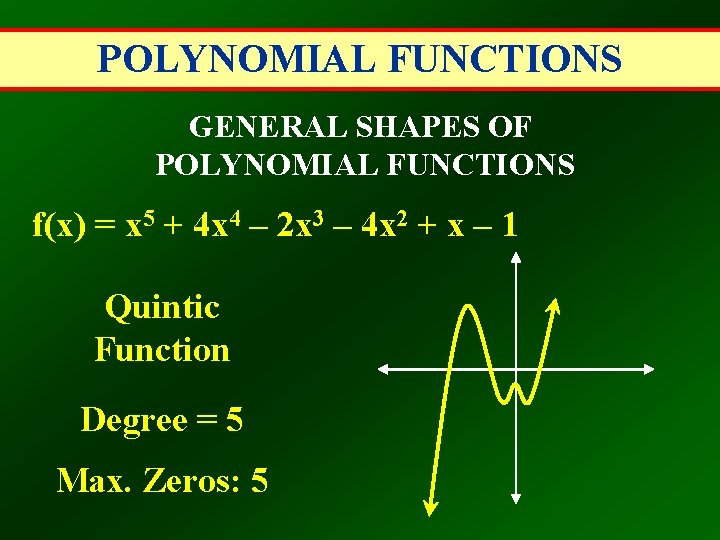
POLYNOMIAL FUNCTIONS GENERAL SHAPES OF POLYNOMIAL FUNCTIONS f(x) = x 5 + 4 x 4 – 2 x 3 – 4 x 2 + x – 1 Quintic Function Degree = 5 Max. Zeros: 5

POLYNOMIAL FUNCTIONS END BEHAVIOR Degree: Even Leading Coefficient: + End Behavior: As x -∞; f(x) +∞ As x +∞; f(x) +∞ f(x) = x 2

POLYNOMIAL FUNCTIONS END BEHAVIOR Degree: Even Leading Coefficient: – End Behavior: As x -∞; f(x) -∞ As x +∞; f(x) -∞ f(x) = -x 2

POLYNOMIAL FUNCTIONS END BEHAVIOR Degree: Odd Leading Coefficient: + End Behavior: As x -∞; f(x) -∞ As x +∞; f(x) +∞ f(x) = x 3

POLYNOMIAL FUNCTIONS END BEHAVIOR Degree: Odd Leading Coefficient: – End Behavior: As x -∞; f(x) +∞ As x +∞; f(x) -∞ f(x) = -x 3

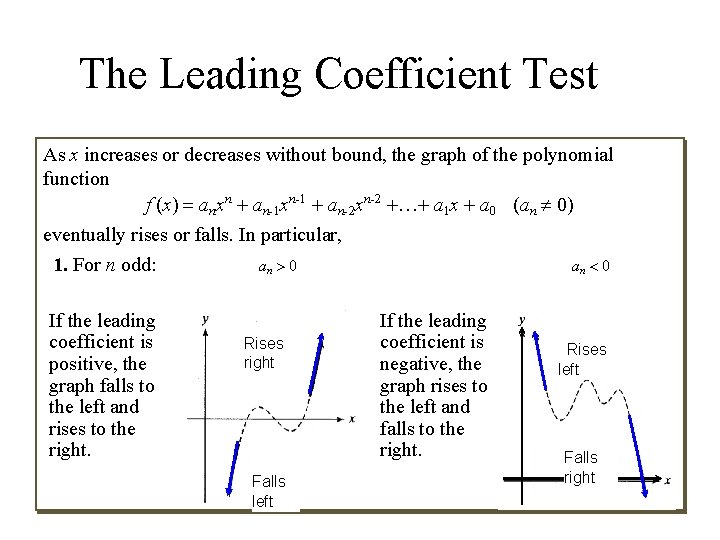
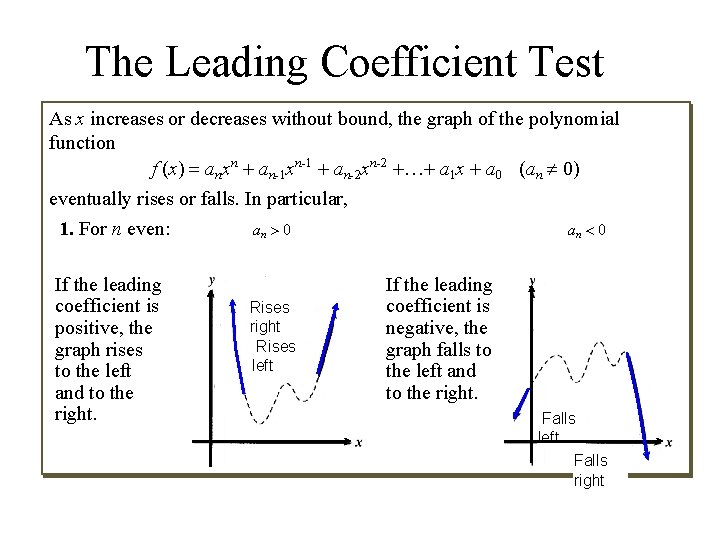
The Leading Coefficient Test As x increases or decreases without bound, the graph of the polynomial function f (x) = anxn + an-1 xn-1 + an-2 xn-2 +…+ a 1 x + a 0 (an ¹ 0) eventually rises or falls. In particular, 1. For n odd: an > 0 an < 0 If the leading coefficient is positive, the graph falls to the left and rises to the right. Rises right Falls left If the leading coefficient is negative, the graph rises to the left and falls to the right. Rises left Falls right

The Leading Coefficient Test As x increases or decreases without bound, the graph of the polynomial function f (x) = anxn + an-1 xn-1 + an-2 xn-2 +…+ a 1 x + a 0 (an ¹ 0) eventually rises or falls. In particular, 1. For n even: an > 0 an < 0 If the leading coefficient is positive, the graph rises to the left and to the right. Rises right Rises left If the leading coefficient is negative, the graph falls to the left and to the right. Falls left Falls right

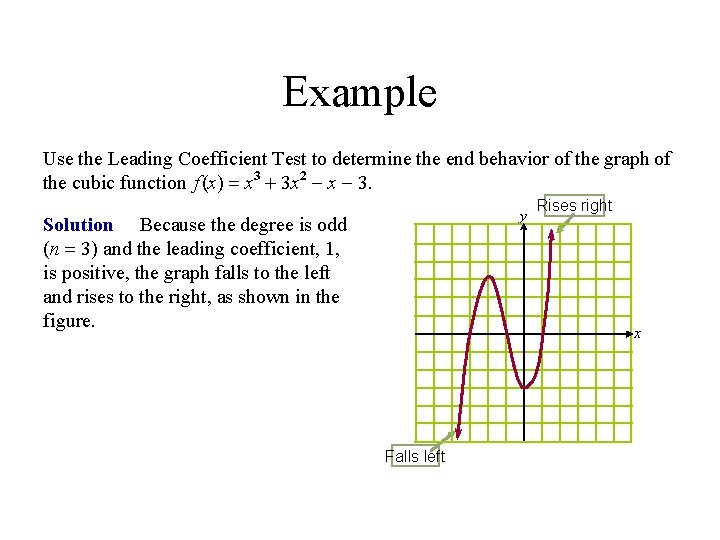
Example Use the Leading Coefficient Test to determine the end behavior of the graph of the cubic function f (x) = x 3 + 3 x 2 - x - 3. y Solution Because the degree is odd (n = 3) and the leading coefficient, 1, is positive, the graph falls to the left and rises to the right, as shown in the figure. Rises right x Falls left

Identifying Polynomial Function Determine whether each function is a polynomial function. If it is determine its degree. No. Variable is the exponent. Yes. Degree is 4.

Identifying Polynomial Function No. Exponent has a negative integer. Yes. Degree is 3.

Identifying Polynomial Function No. The term 1/x can not be written in the form x to the power of n. No. Same as above.

Graphing a Polynomial Function Example Find all zeros of f (x) = -x 4 + 4 x 3 - 4 x 2. Solution We find the zeros of f by setting f (x) equal to 0. -x 4 + 4 x 3 - 4 x 2 = 0 x 4 - 4 x 3 + 4 x 2 = 0 x 2(x 2 - 4 x + 4) = 0 x 2(x - 2)2 = 0 x=0 or (x - 2)2 = 0 x=2 We now have a polynomial equation. Multiply both sides by -1. (optional step) Factor out x 2. Factor completely. Set each factor equal to zero. Solve for x.

Example cont. Graph: f (x) = x 4 - 2 x 2 + 1. Solution Step 1 Determine end behavior. Because the degree is even (n = 4) and the leading coefficient, 1, is positive, the graph rises to the left and the right: y Rises left Rises right x

Example cont. Graph: f (x) = x 4 - 2 x 2 + 1. Solution Step 2 Find the x-intercepts (zeros of the function) by setting f (x) = 0. x 4 - 2 x 2 + 1 = 0 (x 2 - 1) = 0 (x + 1)(x - 1) = 0 (x + 1)2(x - 1)2 = 0 (x + 1)2 = 0 x = -1 or (x - 1)2 = 0 x=1 Factor completely. Express the factoring in more compact notation. Set each factor equal to zero. Solve for x.

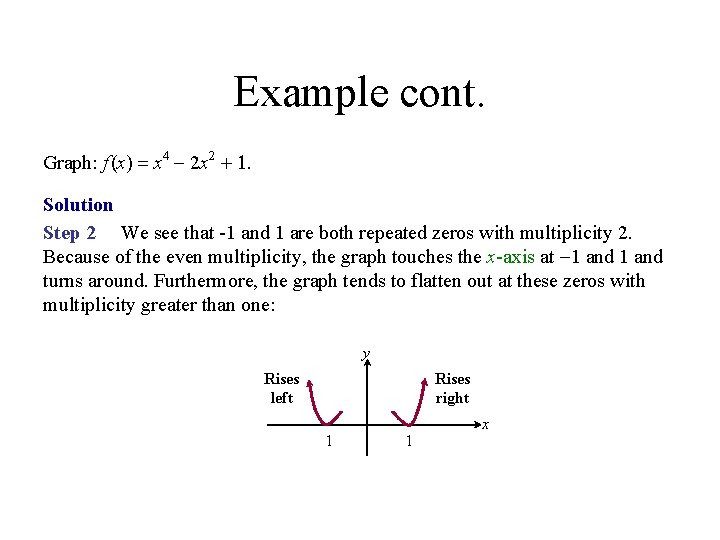
Example cont. Graph: f (x) = x 4 - 2 x 2 + 1. Solution Step 2 We see that -1 and 1 are both repeated zeros with multiplicity 2. Because of the even multiplicity, the graph touches the x-axis at -1 and turns around. Furthermore, the graph tends to flatten out at these zeros with multiplicity greater than one: y Rises right Rises left 1 1 x

Example cont. Graph: f (x) = x 4 - 2 x 2 + 1. Solution Step 3 Find the y-intercept. Replace x with 0 in f (x) = -x + 4 x - 1. f (0) = 04 - 2 • 02 + 1 = 1 There is a y-intercept at 1, so the graph passes through (0, 1). y Rises left Rises right 1 x 1 1

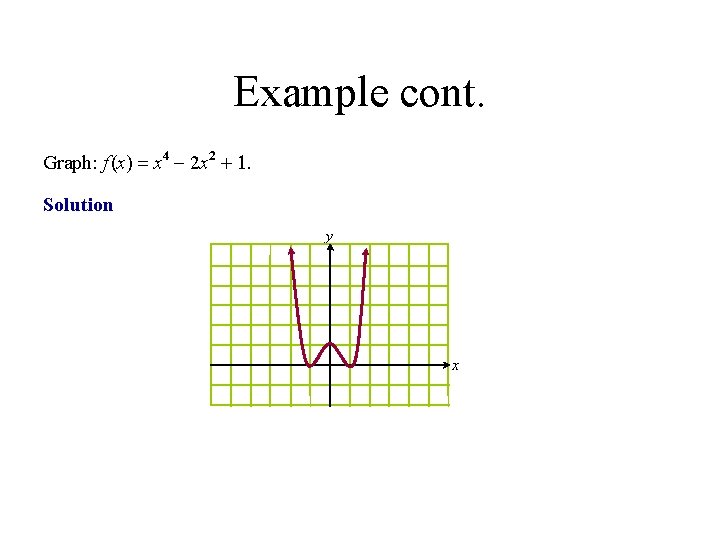
Example cont. Graph: f (x) = x 4 - 2 x 2 + 1. Solution y x
 5-3 polynomial functions
5-3 polynomial functions Polynomial vocabulary
Polynomial vocabulary Polynomial functions and their graphs
Polynomial functions and their graphs Polynomial functions and their graphs
Polynomial functions and their graphs Horizontal asymptote
Horizontal asymptote Quadratic functions and their graphs
Quadratic functions and their graphs 8-3 practice rational functions and their graphs
8-3 practice rational functions and their graphs Chapter 1 functions and their graphs
Chapter 1 functions and their graphs Sketch the graph of the following rational function
Sketch the graph of the following rational function Common functions and their graphs
Common functions and their graphs Exponential functions and their graphs
Exponential functions and their graphs Chapter 2 functions and their graphs answers
Chapter 2 functions and their graphs answers How to find horizontal asymptotes
How to find horizontal asymptotes Lesson 3 rational functions and their graphs
Lesson 3 rational functions and their graphs Investigating graphs of polynomial functions
Investigating graphs of polynomial functions Investigating graphs of functions for their properties
Investigating graphs of functions for their properties 6-7 investigating graphs of polynomial functions
6-7 investigating graphs of polynomial functions 5-4 analyzing graphs of polynomial functions
5-4 analyzing graphs of polynomial functions 6-7 investigating graphs of polynomial functions
6-7 investigating graphs of polynomial functions Unit 5 polynomial functions
Unit 5 polynomial functions 5-4 practice analyzing graphs of polynomial functions
5-4 practice analyzing graphs of polynomial functions Encoding bugs in software testing
Encoding bugs in software testing Graphs that enlighten and graphs that deceive
Graphs that enlighten and graphs that deceive Speed and velocity
Speed and velocity Quadratic graphs and their properties
Quadratic graphs and their properties Expander graphs and their applications
Expander graphs and their applications Lesson 3-1 inequalities and their solutions
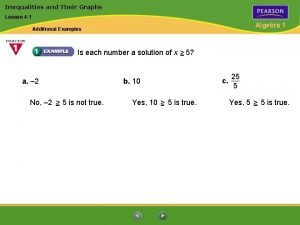
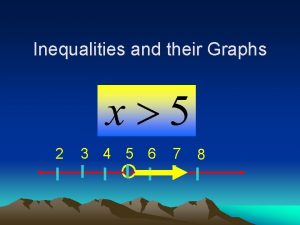
Lesson 3-1 inequalities and their solutions 3-1 inequalities and their graphs
3-1 inequalities and their graphs 3-1 inequalities and their graphs
3-1 inequalities and their graphs