Graphing Polynomial Functions Graphs of Polynomial Functions 1




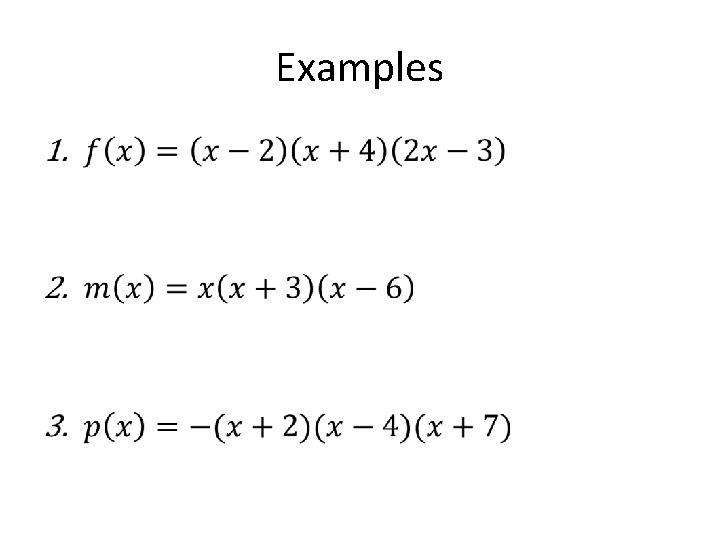

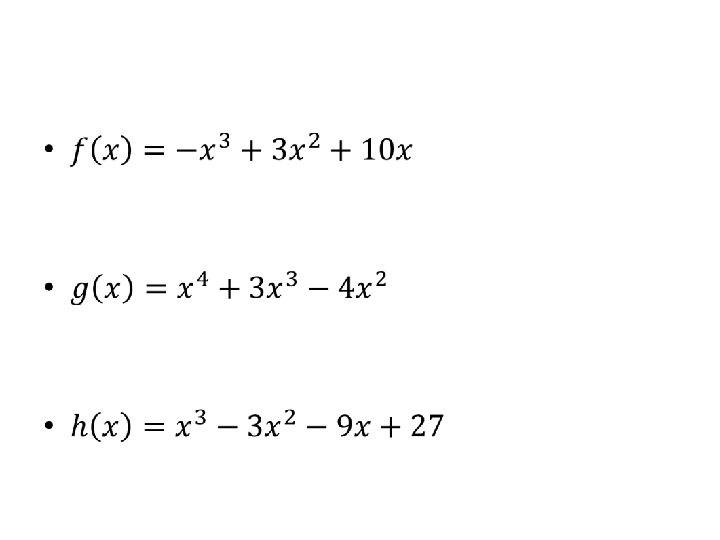
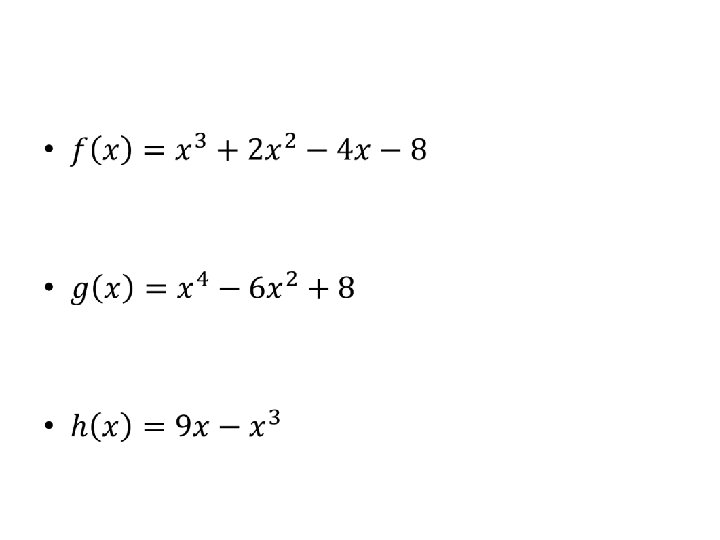





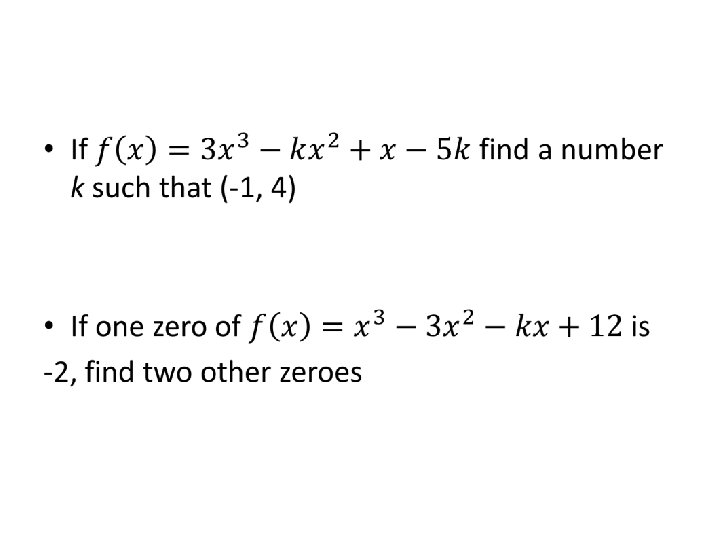










- Slides: 24

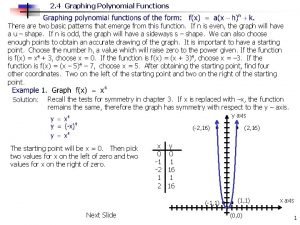
Graphing Polynomial Functions

Graphs of Polynomial Functions • 1. Polynomials have smooth, continuous curves • 2. Continuous means it can be drawn without picking up a pencil • 3. Smooth means it have no sharp points

• 1. Even powers are tangent to the x-axis • 2. Odd powers go across the x-axis at the origin • 3. As the power increases, the curve gets wider at the point of tangency or intersection

Steps for graphing polynomial functions: • • 1. find zeroes 2. Make a number line 3. determine positive and negative values 4. sketch graph
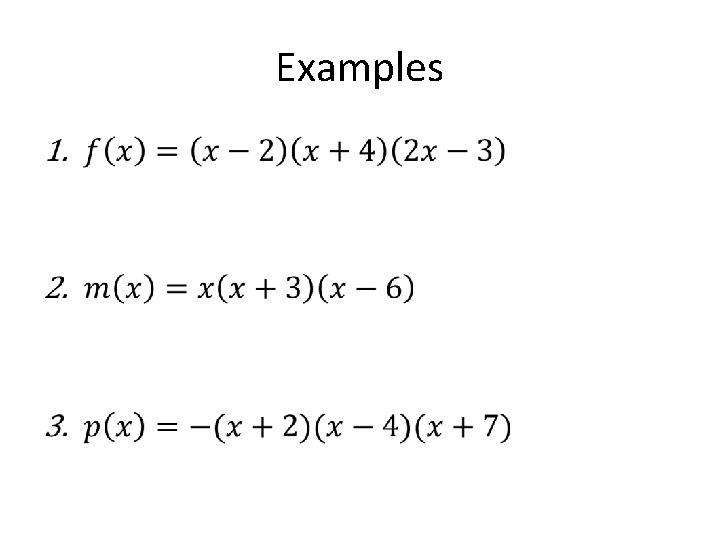
Examples •

Double Roots •
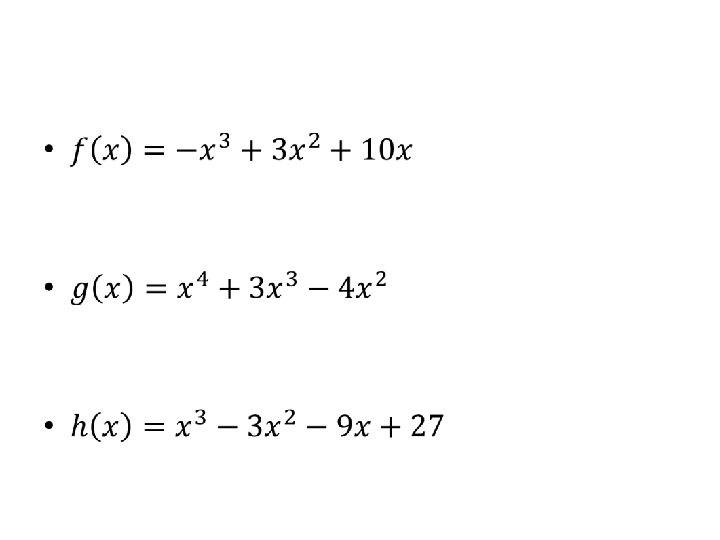
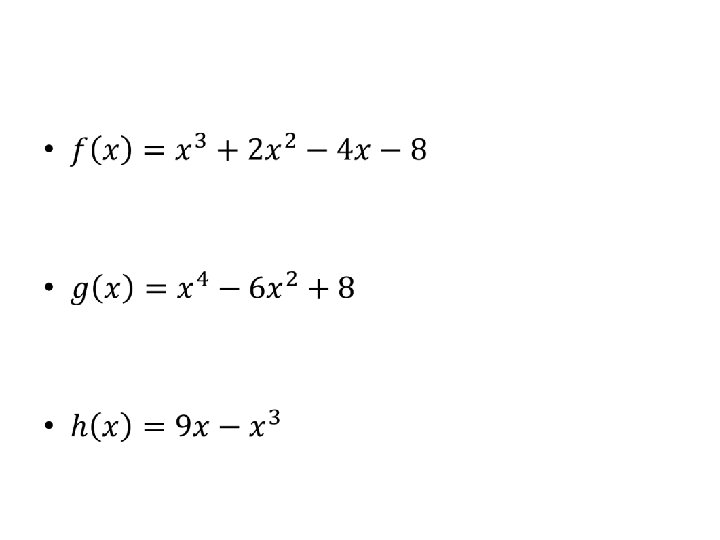

Polynomial Division •

Long Division • Check for placeholders, leave variables • Change signs

Synthetic Division • Find zeros • Check for placeholders • Divide zero into coefficients of polynomial function (multiply, add, repeat)

Remainder Theorem • Let f be a polynomial function. If f(x) is divdied by x-c, then remainder is f(c) • PROOF • When f(x) is divided by x-c, the remainder must be a constant, r, (because the remainder must have a smaller degree than x-c) so by the division algorithm: • f(x)=q(x)(x-c)+r • In order to find f(c), substitute c in for x • f(c)=q(c)(c-c)+r = q(c)0+r = r • So f(c)=r

Factor Theorem • Let f be a polynomial functions. Then x-c is a factor of f(x) if and only if (iff) f(c)=0 • PROOF (must prove both ways) • 1. If x-c is a factor, then when f(x) is divided by x-c the remainder is 0. By the remainder theorem, f(c)=the remainder, so f(c)=0 • 2. If f(c)=0, the remainder theorem, the remainder when f(x) is divided by x-c is 0. If the remainder is 0, then that means x-c goes into f(x), so x-c is a factor of f(x)
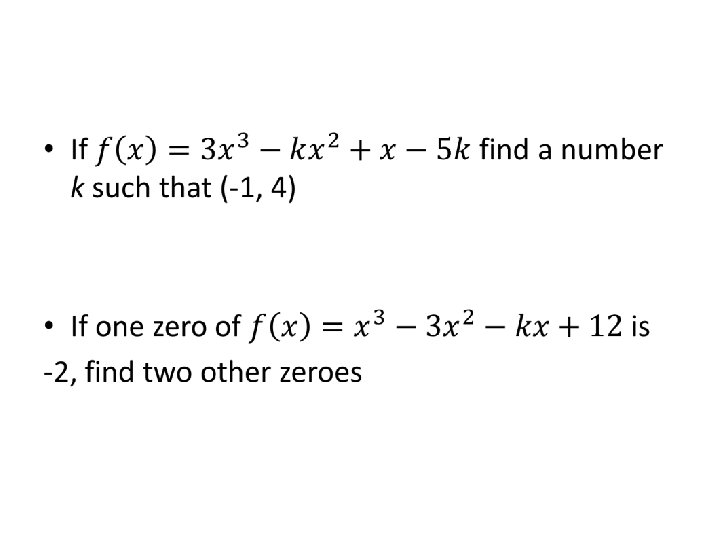

Things you know given f(3)=0 • • • 1. When x=3, y=0 2. (3, 0) is an ordered pair on the graph 3. x-3 is a factor of f(x) 4. when f(x) is divided by x-3, the remainder is 0 5. 3 is a root 6. 3 is an x-intercept 7. 3 is a solution if f(x)=0 8. f(x) touches the x-axis at 3 9. f(x) has a zero at 3 10. if the inverse of f(x) exists, then (0, 3) is on it

Things you know if f(-2)=5 • • • 1. When f(x) is divided by x+2, the remainder is 5 2. x+2 is not a factor of f(x) 3. The point (-2, 5) is on f(x) 4. when x= -2, y=5 5. If the inverse of f(x) exists, then the point (5, 2) is on it 6. -2 is not an x-intercept of f(x) 7. -2 is not a solution to f(x)=0 8. -2 is not a root of f(x) 9. -2 is not a zero of f(x)

Rational Zeros Theorem (P/Q) • =

After you identify possible zeros, find actual • Substitute possible zeros into f(x) OR do synthetic division 1 1 -4 -4 16 1 -3 -7 -9 Remainder is not 0, so 1 isn’t a root 2 1 -4 -4 16 2 -4 -16 1 -2 -8 0 Remainder is 0, so 2 is a root. Take coefficients and continue solving for other roots. -1 1 -4 -4 16 -1 5 -1 1 -5 1 15 Remainder is not 0, so -1 isn’t a root

Fundamental Theorem of Algebra • If f(x) is a polynomial function of degree n, where n>0, f(x) has n zeros in the complex number system • Number of answers= degree

Linear Factorization Theorem •

Irrational Conjugate Theorem •

Complex Conjugate Theorem •

Odd Degree Theorem • Any polynomial with real coefficients and with odd degree must have at least one real zero • (x+2 i)(x-5) 5 is real

Factors of a Polynomial •
 End behavior of polynomials
End behavior of polynomials Unit 5 homework 2 graphing polynomial functions
Unit 5 homework 2 graphing polynomial functions What is the coefficient in polynomials
What is the coefficient in polynomials (-2 4) graph
(-2 4) graph Power function end behavior model
Power function end behavior model Lesson 5-2 graphing polynomial functions answers
Lesson 5-2 graphing polynomial functions answers Polynomial vocabulary
Polynomial vocabulary Practice a investigating graphs of polynomial functions
Practice a investigating graphs of polynomial functions Investigating graphs of polynomial functions
Investigating graphs of polynomial functions Investigating graphs of polynomial functions
Investigating graphs of polynomial functions 5-4 analyzing graphs of polynomial functions
5-4 analyzing graphs of polynomial functions Polynomial functions and their graphs
Polynomial functions and their graphs Investigating graphs of polynomial functions
Investigating graphs of polynomial functions Polynomial functions and their graphs
Polynomial functions and their graphs Unit 5 polynomial functions
Unit 5 polynomial functions 5-4 practice analyzing graphs of polynomial functions
5-4 practice analyzing graphs of polynomial functions State graph in software testing
State graph in software testing Speed and velocity
Speed and velocity Graphs that enlighten and graphs that deceive
Graphs that enlighten and graphs that deceive Leading coefficient of a graph
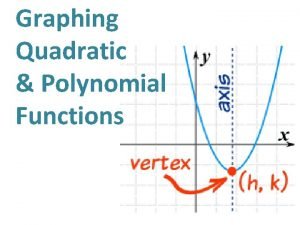
Leading coefficient of a graph Quadratic and polynomial functions
Quadratic and polynomial functions Graphing of polynomial function
Graphing of polynomial function Polynomial inequalities word problems
Polynomial inequalities word problems End behavior of polynomials
End behavior of polynomials Polynomial
Polynomial