5 3 Polynomial Functions Polynomial functions A polynomial

5. 3 Polynomial Functions

Polynomial functions. A polynomial in one variable is a function in the form f(x) = 5 x 8 + 3 x 7 – 8 x 6 + … + 2 x 1 + 11 an is the leading coefficient n is the degree of the polynomial a 0 is the constant term

Type of polynomial DEGREE 0 TYPE Constant 1 Linear 2 Quadratic 3 Cubic 4 Quartic

Example 1 : Answer these questions for the following functions. Is it a polynomial in one variable? Explain. What is the degree of the polynomial What is the leading coefficient of the polynomial? What is the constant (y-intercept) of the polynomial? What type of polynomial is it? a. f(x) = 3 x 2 + 3 x 3 – 7 x 4 + x – 6 b. f(x, y) = 4 x 5 – 14 xy 4 + x – 6 c. f(y) = (5 – 4 y)(6 + 2 y)

To evaluate a function, you need to plug a value into the function. Example 2: a) f(x) = 3 x 5 – x 4 – 5 x + 10 Find f(– 2)

To evaluate a function, you need to plug a value into the function. Example 2: b) f(x) = x 5 – x 4 – 5 x + 10 and g(x) = 2 x 3 – x – 5 Find f(3 d)

To evaluate a function, you need to plug a value into the function. Example 2: c) f(x) = x 5 – x 4 – 5 x + 10 and g(x) = 2 x 3 – x – 5 Find g(p 2)

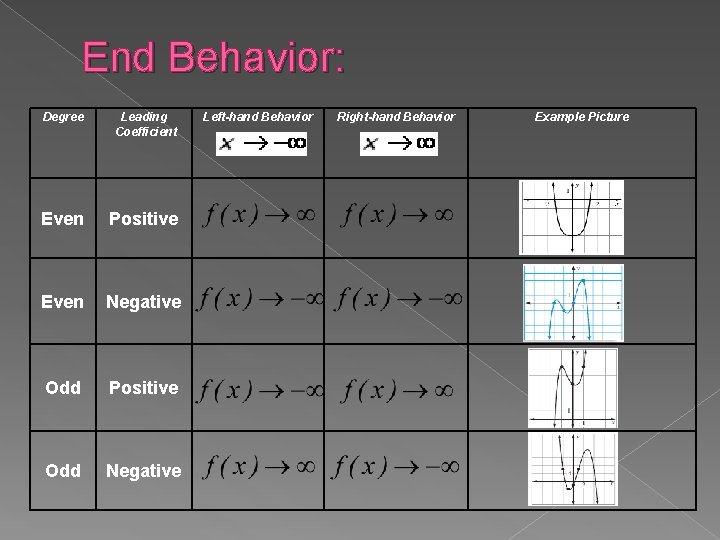
End Behavior: Degree Leading Coefficient Even Positive Even Negative Odd Positive Odd Negative Left-hand Behavior Right-hand Behavior Example Picture

Example 5: Describe the end behavior for each polynomial. a. f(x) = 3 x 5 – x 4 – 5 x + 10 b. f(x) = 3 x 3 – 4 x 6 + 2 x

Real Zeros The x-intercepts of the function.

Degree of polynomial Turning points – the points on a graph where the function changes its vertical direction (up/down). If the degree of the polynomial is n, there will be at most n – 1 turning points Ex) If a polynomial has 8 turning points then the degree is ____.

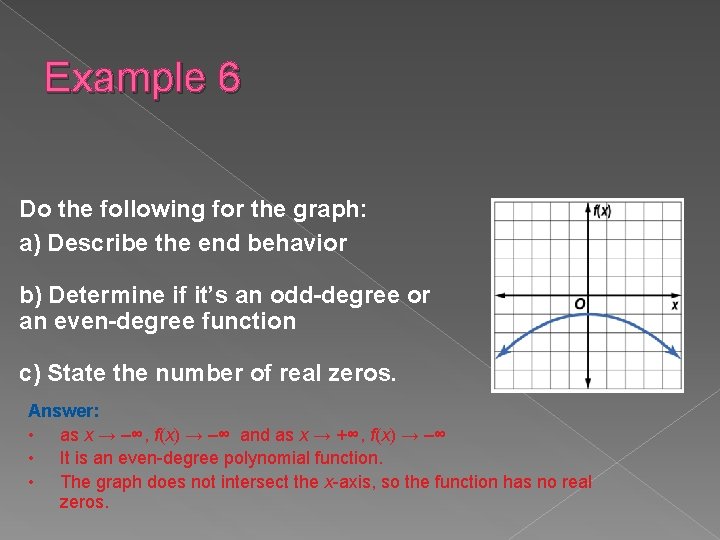
Example 6 Do the following for the graph: a) Describe the end behavior b) Determine if it’s an odd-degree or an even-degree function c) State the number of real zeros. Answer: • as x → –∞, f(x) → –∞ and as x → +∞, f(x) → –∞ • It is an even-degree polynomial function. • The graph does not intersect the x-axis, so the function has no real zeros.

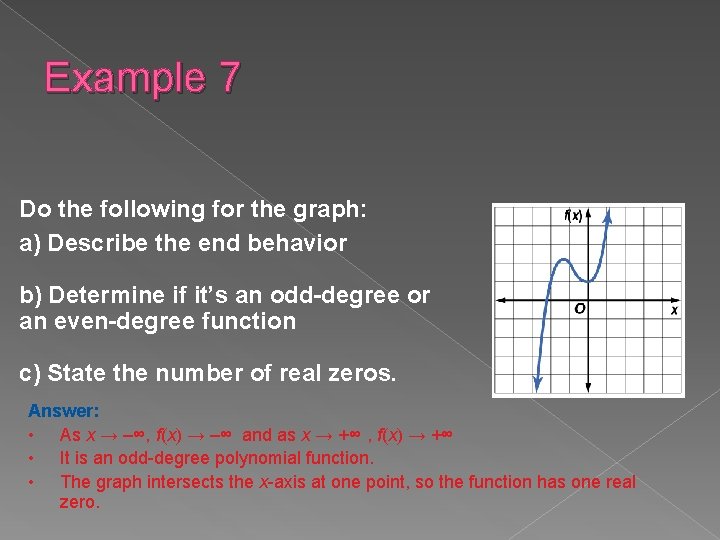
Example 7 Do the following for the graph: a) Describe the end behavior b) Determine if it’s an odd-degree or an even-degree function c) State the number of real zeros. Answer: • As x → –∞, f(x) → –∞ and as x → +∞ , f(x) → +∞ • It is an odd-degree polynomial function. • The graph intersects the x-axis at one point, so the function has one real zero.