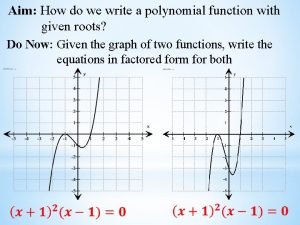
Polynomial Functions EVALUATING POLYNOMIAL FUNCTIONS A polynomial function




















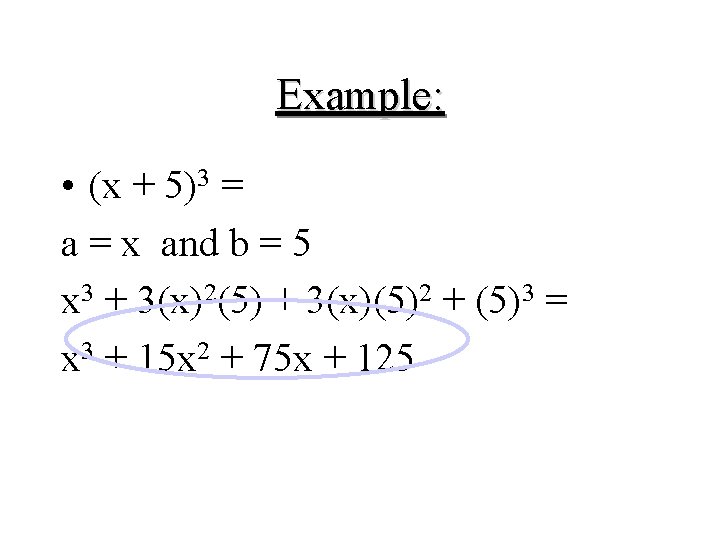



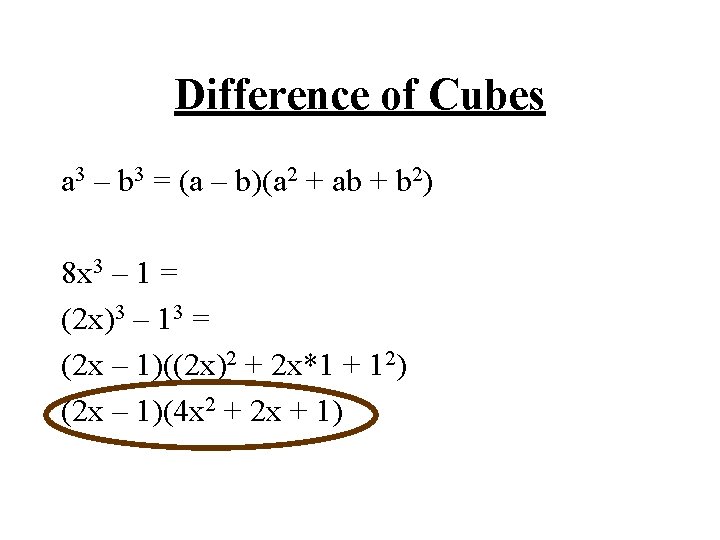


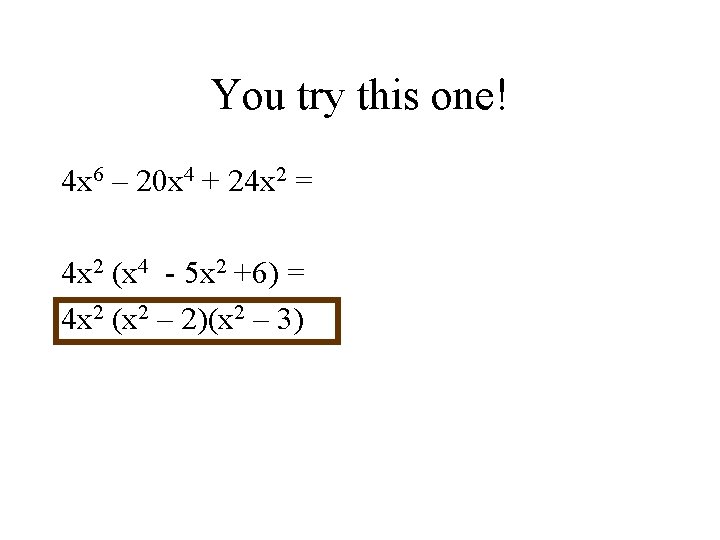

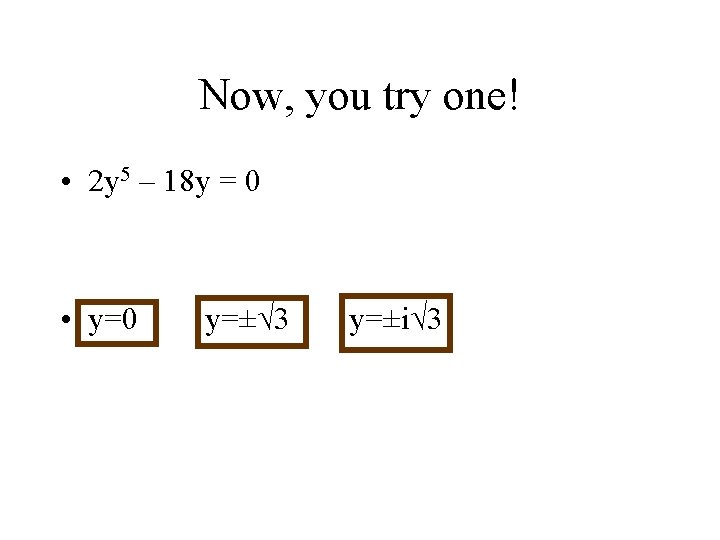
- Slides: 33

Polynomial Functions

EVALUATING POLYNOMIAL FUNCTIONS A polynomial function is a function of the form f (x) = an x nn + an – 1 x nn – 11 +· · ·+ a 1 x + aa 0 0 Where aann >0 0 and the exponents are all whole numbers. coefficient For this polynomial function, aann is the leading coefficient, constant term, term and n is the degree aa 00 is the constant A polynomial function is in standard form if its terms are descending order of of exponents from left to to right. written in descending

EVALUATING POLYNOMIAL FUNCTIONS You are already familiar with some types of polynomial functions. Here is a summary of common types of polynomial functions. Degree Type Standard Form 0 Constant f (x) = a 0 1 Linear f (x) = a 1 x + a 0 2 Quadratic f (x) = a 2 x 2 + a 1 x + a 0 3 Cubic f (x) = a 3 x 3 + a 2 x 2 + a 1 x + a 0 4 Quartic f (x) = a 4 x 4 + a 3 x 3 + a 2 x 2 + a 1 x + a 0

Identifying Polynomial Functions Decide whether the function is a polynomial function. If it is, write the function in standard form and state its degree, type and leading coefficient. f (x) = 1 x 2 – 3 x 4 – 7 2 SOLUTION The function is a polynomial function. Its standard form is f (x) = – 3 x 4 + 1 2 x – 7. 2 It has degree 4, so it is a quartic function. The leading coefficient is – 3.

Identifying Polynomial Functions Decide whether the function is a polynomial function. If it is, write the function in standard form and state its degree, type and leading coefficient. f (x) = x 3 + 3 x SOLUTION The function is not a polynomial function because the x term 3 does not have a variable base and an exponent that is a whole number.

Identifying Polynomial Functions Decide whether the function is a polynomial function. If it is, write the function in standard form and state its degree, type and leading coefficient. – f (x) = 6 x 2 + 2 x 1 + x SOLUTION The function is not a polynomial function because the term 2 x – 1 has an exponent that is not a whole number.

Identifying Polynomial Functions Polynomial function? f (x) = 12 x 2 – 3 x 4 – 7 f (x) = x 3 + 3 x f (x) = 6 x 2 + 2 x– 1 + x

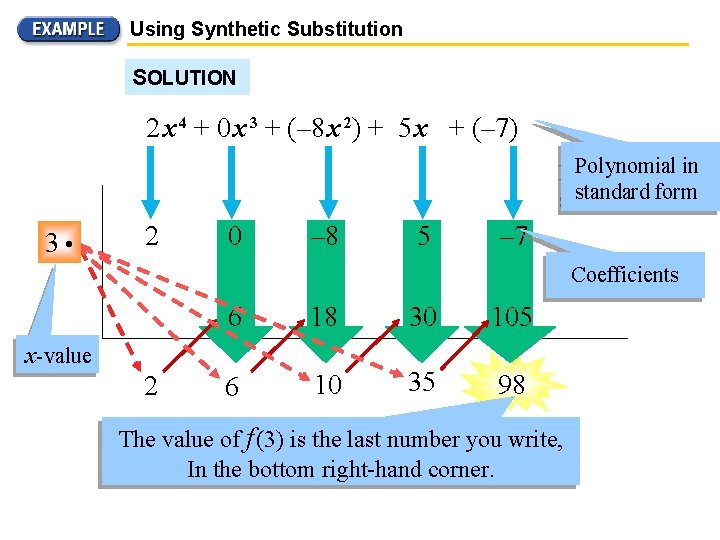
Using Synthetic Substitution One way to evaluate polynomial functions is to use direct substitution. Another way to evaluate a polynomial is to use synthetic substitution. Use synthetic division to evaluate f (x) = 2 x 4 + -8 x 2 + 5 x - 7 when x = 3.

Using Synthetic Substitution SOLUTION 2 x 4 + 0 x 3 + (– 8 x 2) + 5 x + (– 7) Polynomialinin Polynomial standardform standard 33 • 2 0 – 8 5 – 7 Coefficients 6 18 30 105 6 10 35 98 x-value 2 The value of f (3) is the last number you write, In the bottom right-hand corner.

GRAPHING POLYNOMIAL FUNCTIONS The end behavior of a polynomial function’s graph is the behavior of the graph as x approaches infinity (+ ∞) or negative infinity (– ∞). The expression x + ∞ is read as “x approaches positive infinity. ”

GRAPHING POLYNOMIAL FUNCTIONS END BEHAVIOR

GRAPHING POLYNOMIAL FUNCTIONS CONCEPT SUMMARY END BEHAVIOR FOR POLYNOMIAL FUNCTIONS x +∞ +∞ f (x) –∞ f (x) +∞ even f (x) –∞ odd f (x) +∞ f (x) –∞ an n x >0 even f (x) >0 odd <0 <0 –∞

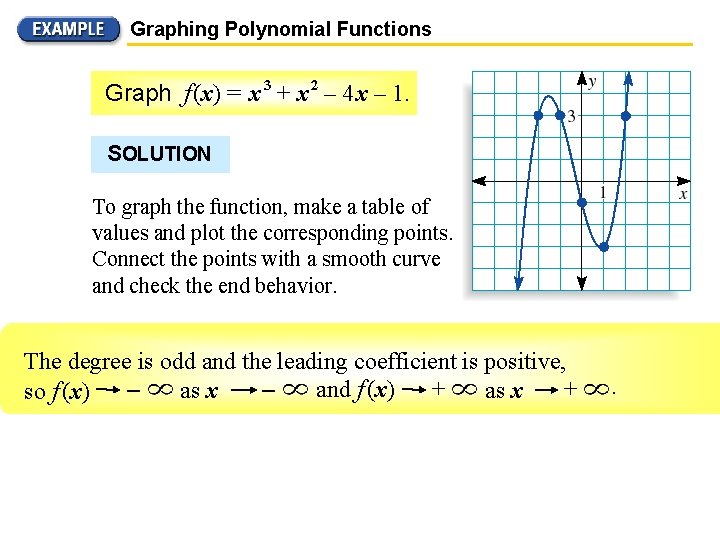
Graphing Polynomial Functions Graph f (x) = x 3 + x 2 – 4 x – 1. SOLUTION To graph the function, make a table of values and plot the corresponding points. Connect the points with a smooth curve and check the end behavior. – 3 and– 2 – 1 coefficient 0 1 is positive, 2 3 x The degree is odd the leading 3 and f (x) – 1 + – 3 as x 3 + 23. so f (x) f(x)– – 7 as x 3 –

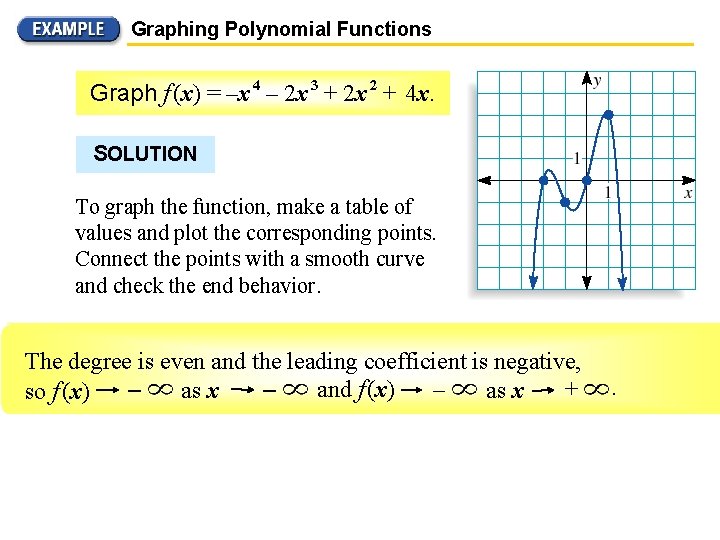
Graphing Polynomial Functions Graph f (x) = –x 4 – 2 x 3 + 2 x 2 + 4 x. SOLUTION To graph the function, make a table of values and plot the corresponding points. Connect the points with a smooth curve and check the end behavior. – 2 the leading – 1 0 coefficient 1 is negative, 2 3 x The degree is– 3 even and – 16 +. as x – 105 so f (x) – – 21 as x 0 – – 1 and f 0(x) 3–

Adding, Subtracting, & Multiplying Polynomials

To + or - , + or – the coeff. of like terms! Vertical format : • Add 3 x 3+2 x 2 -x-7 and x 3 -10 x 2+8. • 3 x 3 + 2 x 2 – x – 7 + x 3 – 10 x 2 + 8 Line up like terms • 4 x 3 – 8 x 2 – x + 1

Horizontal format : Combine like terms • (8 x 3 – 3 x 2 – 2 x + 9) – (2 x 3 + 6 x 2 – x + 1)= • (8 x 3 – 2 x 3)+(-3 x 2 – 6 x 2)+(-2 x + x) + (9 – 1)= • 6 x 3 + -9 x 2 + -x + 8= • 6 x 3 – 9 x 2 – x + 8

Examples: Adding & Subtracting • (9 x 3 – 2 x + 1) + (5 x 2 + 12 x -4) = • 9 x 3 + 5 x 2 – 2 x + 1 – 4 = • 9 x 3 + 5 x 2 + 10 x – 3 • • (2 x 2 + 3 x) – (3 x 2 + x – 4)= 2 x 2 + 3 x – 3 x 2 – x + 4 = 2 x 2 - 3 x 2 + 3 x – x + 4 = -x 2 + 2 x + 4

Multiplying Polynomials: Vertically • (-x 2 + 2 x + 4)(x – 3)= -x 2 + 2 x + 4 * x– 3 3 x 2 – 6 x – 12 -x 3 + 2 x 2 + 4 x -x 3 + 5 x 2 – 2 x – 12

Multiplying Polynomials : Horizontally • • (x – 3)(3 x 2 – 2 x – 4)= (x – 3)(3 x 2) + (x – 3)(-2 x) + (x – 3)(-4) = (3 x 3 – 9 x 2) + (-2 x 2 + 6 x) + (-4 x + 12) = 3 x 3 – 9 x 2 – 2 x 2 + 6 x – 4 x +12 = 3 x 3 – 11 x 2 + 2 x + 12

Multiplying 3 Binomials : • • (x – 1)(x + 4)(x + 3) = FOIL the first two: (x 2 – x +4 x – 4)(x + 3) = (x 2 + 3 x – 4)(x + 3) = Then multiply the trinomial by the binomial (x 2 + 3 x – 4)(x) + (x 2 + 3 x – 4)(3) = (x 3 + 3 x 2 – 4 x) + (3 x 2 + 9 x – 12) = x 3 + 6 x 2 + 5 x - 12

Some binomial products appear so much we need to recognize the patterns! • Sum & Difference (S&D): • (a + b)(a – b) = a 2 – b 2 • Example: (x + 3)(x – 3) = x 2 – 9 • Square of Binomial: • (a + b)2 = a 2 + 2 ab + b 2 • (a - b)2 = a 2 – 2 ab + b 2

Last Pattern • Cube of a Binomial • (a + b)3 = a 3 + 3 a 2 b + 3 ab 2 + b 3 • (a – b)3 = a 3 - 3 a 2 b + 3 ab 2 – b 3
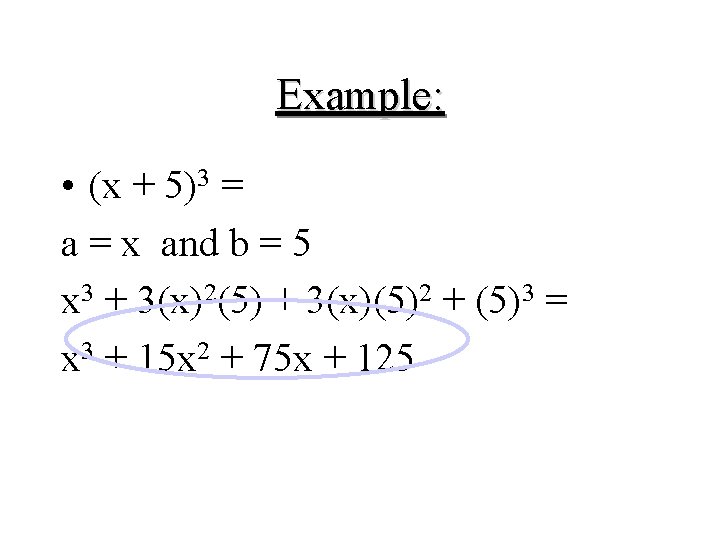
Example: • (x + 5)3 = a = x and b = 5 x 3 + 3(x)2(5) + 3(x)(5)2 + (5)3 = x 3 + 15 x 2 + 75 x + 125

Factoring and Solving Polynomial Expressions

Types of Factoring: – GCF : 6 x 2 + 15 x = 3 x (2 x + 5) – POS : x 2 + 10 x + 25 = (x + 5)2 – DOS : 4 x 2 – 9 = (2 x + 3)(2 x – 3) – “Bustin’ da B” = 2 x 2 – 5 x – 12 = » (2 x 2 - 8 x) + (3 x – 12) = » 2 x(x – 4) + 3(x – 4)= » (x – 4)(2 x + 3)

Now we will use Sum of Cubes: a 3 + b 3 = (a + b)(a 2 – ab + b 2) x 3 + 8 = (x)3 + (2)3 = (x + 2)(x 2 – 2 x + 4)
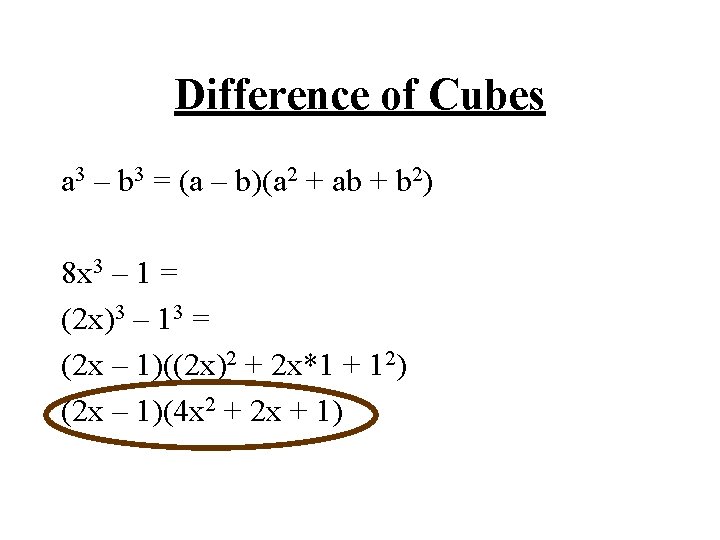
Difference of Cubes a 3 – b 3 = (a – b)(a 2 + ab + b 2) 8 x 3 – 1 = (2 x)3 – 13 = (2 x – 1)((2 x)2 + 2 x*1 + 12) (2 x – 1)(4 x 2 + 2 x + 1)

When there are more than 3 terms – use GROUPING x 3 – 2 x 2 – 9 x + 18 = (x 3 – 2 x 2) + (-9 x + 18) = x 2(x – 2) - 9(x – 2) = (x – 2)(x 2 – 9) = (x – 2)(x + 3)(x – 3) Group in two’s with a ‘+’ in the middle GCF each group Factor all that can be factored

Factoring in Quad form: 81 x 4 – 16 = (9 x 2)2 – 42 = (9 x 2 + 4)(9 x 2 – 4)= Can anything be factored still? ? ? (9 x 2 + 4)(3 x – 2)(3 x +2) Keep factoring ‘till you can’t factor any more!!
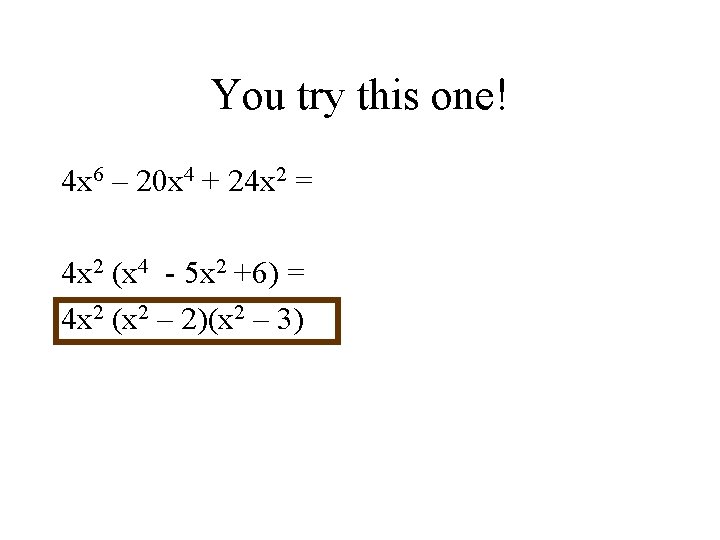
You try this one! 4 x 6 – 20 x 4 + 24 x 2 = 4 x 2 (x 4 - 5 x 2 +6) = 4 x 2 (x 2 – 2)(x 2 – 3)

Solve: • 2 x 5 + 24 x = 14 x 3 2 x 5 - 14 x 3 + 24 x = 0 2 x (x 4 – 7 x 2 +12) = 0 2 x (x 2 – 3)(x 2 – 4) = 0 2 x (x 2 – 3)(x + 2)(x – 2) = 0 2 x=0 x 2 -3=0 x+2=0 x=±√ 3 x=-2 Put in standard form GCF Bustin’ da ‘b’ Factor EVERYTHING x-2=0 set all to zero x=2
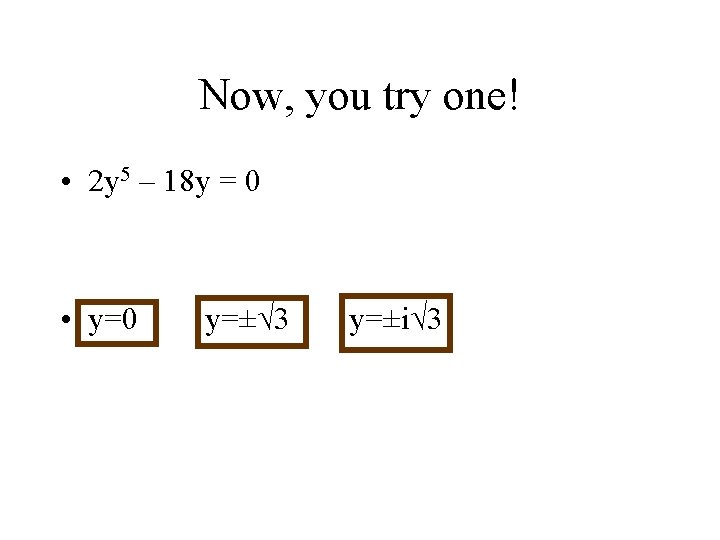
Now, you try one! • 2 y 5 – 18 y = 0 • y=0 y=±√ 3 y=±i√ 3
 Evaluating polynomial functions
Evaluating polynomial functions Evaluating polynomial functions
Evaluating polynomial functions Function notation and evaluating functions
Function notation and evaluating functions Evaluating functions and operations on functions
Evaluating functions and operations on functions Evaluating functions and operations on functions
Evaluating functions and operations on functions Identifying polynomial functions
Identifying polynomial functions Polynomial function parent function
Polynomial function parent function Power function vs polynomial function
Power function vs polynomial function 15.1 defining and evaluating a logarithmic function
15.1 defining and evaluating a logarithmic function Sin 45 exact value
Sin 45 exact value How do you solve piecewise functions
How do you solve piecewise functions Evaluating inverse trig functions without a calculator
Evaluating inverse trig functions without a calculator Evaluating composite functions using tables
Evaluating composite functions using tables How to write a exponential function from a table
How to write a exponential function from a table Evaluating an arithmetic combination of functions
Evaluating an arithmetic combination of functions Inverse trig quadrants
Inverse trig quadrants Composite functions domain and range practice
Composite functions domain and range practice Matplotlib inline
Matplotlib inline How to divide a polynomial by another polynomial
How to divide a polynomial by another polynomial Nth degree polynomial function
Nth degree polynomial function Third degree polynomial function
Third degree polynomial function Roots of a polynomial
Roots of a polynomial Zeros and multiplicity
Zeros and multiplicity Power function بالعربي
Power function بالعربي Find the end behavior of a polynomial function
Find the end behavior of a polynomial function Critical path motion
Critical path motion Polynomial standard form
Polynomial standard form Finding real roots of polynomial equations examples
Finding real roots of polynomial equations examples Zeros where the graph touches but does not cross the x-axis
Zeros where the graph touches but does not cross the x-axis Pg
Pg Polynomial function word problem
Polynomial function word problem Even degree polynomial
Even degree polynomial Polynomial constant term
Polynomial constant term Transforming polynomial functions
Transforming polynomial functions