Digital Lesson Polynomial Functions A polynomial function is

Digital Lesson Polynomial Functions

A polynomial function is a function of the form where n is a nonnegative integer and each ai (i = 0, , n) is a real number. The polynomial function has a leading coefficient an and degree n. Examples: Find the leading coefficient and degree of each polynomial function. Polynomial Function Copyright © by Houghton Mifflin Company, Inc. All rights reserved. Leading Coefficient Degree – 2 5 1 3 14 0 2

A real number a is a zero of a function y = f (x) if and only if f (a) = 0. Real Zeros of Polynomial Functions If y = f (x) is a polynomial function and a is a real number then the following statements are equivalent. 1. x = a is a zero of f. 2. x = a is a solution of the polynomial equation f (x) = 0. 3. (x – a) is a factor of the polynomial f (x). 4. (a, 0) is an x-intercept of the graph of y = f (x). A polynomial function of degree n has at most n zeros. Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 3

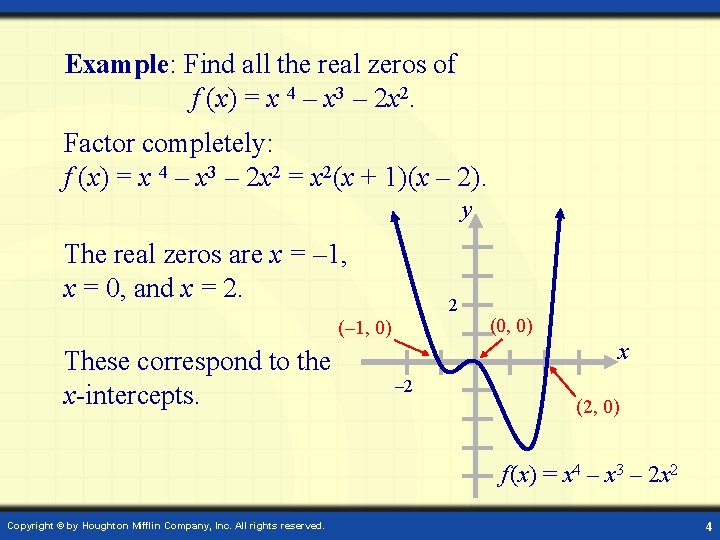
Example: Find all the real zeros of f (x) = x 4 – x 3 – 2 x 2. Factor completely: f (x) = x 4 – x 3 – 2 x 2 = x 2(x + 1)(x – 2). y The real zeros are x = – 1, x = 0, and x = 2. 2 (– 1, 0) These correspond to the x-intercepts. (0, 0) x – 2 (2, 0) f (x) = x 4 – x 3 – 2 x 2 Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 4

Dividing Polynomials Example: Divide x 2 + 3 x – 2 by x – 1 and check the answer. x + 2 x 2 + x 2 x – 2 2 x + 2 – 4 remainder Answer: x + 2 + – 4 1. 2. 3. 4. 5. 6. Check: (x + 2) (x + 1) + (– 4) = x 2 + 3 x – 2 quotient divisor remainder Copyright © by Houghton Mifflin Company, Inc. All rights reserved. dividend 5

Synthetic division is a shorter method of dividing polynomials. This method can be used only when the divisor is of the form x – a. It uses the coefficients of each term in the dividend. Example: Divide 3 x 2 + 2 x – 1 by x – 2 using synthetic division. Since the divisor is x – 2, a = 2. coefficients of the dividend value of a 2 3 3 2 – 1 6 16 8 15 coefficients of quotient Answer: 3 x + 8 Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 1. Bring down 3 2. (2 • 3) = 6 3. (2 + 6) = 8 4. (2 • 8) = 16 5. (– 1 + 16) = 15 remainder 15 6

Remainder Theorem: The remainder of the division of a polynomial f (x) by x – k is f (k). Example: Using the remainder theorem, evaluate f(x) = x 4 – 4 x – 1 when x = 3. value of x 3 1 1 0 0 – 4 – 1 3 9 27 69 3 9 23 68 The remainder is 68 at x = 3, so f (3) = 68. You can check this using substitution: f(3) = (3)4 – 4(3) – 1 = 68. Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 7

Factor Theorem: A polynomial f(x) has a factor (x – k) if and only if f(k) = 0. Example: Show that (x + 2) and (x – 1) are factors of f(x) = 2 x 3 + x 2 – 5 x + 2. – 2 2 2 1 – 5 2 – 4 6 – 2 – 3 1 0 1 2 2 – 3 1 2 – 1 0 The remainders of 0 indicate that (x + 2) and (x – 1) are factors. The complete factorization of f is (x + 2)(x – 1)(2 x – 1). Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 8

Rational Zero Test: If a polynomial f(x) has integer coefficients, every rational zero of f has the form where p and q have no common factors other than 1. • p is a factor of the constant term. • q is a factor of the leading coefficient. Example: Find the rational zeros of f(x) = x 3 + 3 x 2 – x – 3. q=1 p=– 3 The possible rational zeros are ± 1 and ± 3. Synthetic division shows that the factors of f are (x + 3), (x + 1), and (x – 1). The zeros of f are – 3, – 1, and 1. Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 9

Descartes’s Rule of Signs: If f(x) is a polynomial with real coefficients and a nonzero constant term, 1. The number of positive real zeros of f is equal to the number of variations in sign of f(x) or less than that number by an even integer. 2. The number of negative real zeros of f is equal to the number of variations in sign of f(–x) or less than that number by an even integer. A variation in sign means that two consecutive, nonzero coefficients have opposite signs. Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 10

Example: Use Descartes’s Rule of Signs to determine the possible number of positive and negative real zeros of f(x) = 2 x 4 – 17 x 3 + 35 x 2 + 9 x – 45. The polynomial has three variations in sign. + to – f(x) = 2 x 4 – 17 x 3 + 35 x 2 + 9 x – 45 – to + f(x) has either three positive real zeros or one positive real zero. f(– x) = 2(– x)4 – 17(– x)3 + 35(– x)2 + 9(– x) – 45 =2 x 4 + 17 x 3 + 35 x 2 – 9 x – 45 f(x) has one negative real zero. One change in sign f(x) = 2 x 4 – 17 x 3 + 35 x 2 + 9 x – 45 = (x + 1)(2 x – 3)(x – 5). Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 11

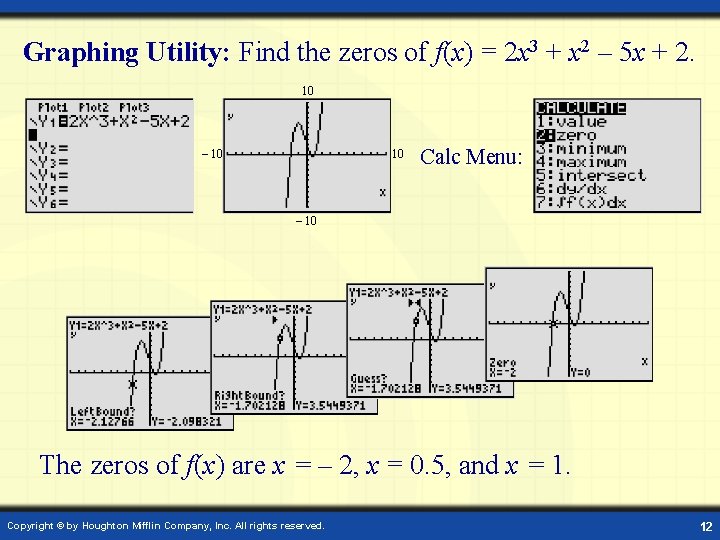
Graphing Utility: Find the zeros of f(x) = 2 x 3 + x 2 – 5 x + 2. 10 – 10 10 Calc Menu: – 10 The zeros of f(x) are x = – 2, x = 0. 5, and x = 1. Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 12