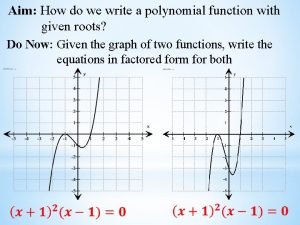
Polynomial Functions Lesson 9 2 Power Function Definition

Polynomial Functions Lesson 9. 2

Power Function • Definition • Recall from the chapter on shifting and stretching, what effect the k will have? § Vertical stretch or compression for k < 1

Special Power Functions • Parabola y = x 2 • Cubic function y = x 3 • Hyperbola y = x-1

Special Power Functions • y = x-2 • •

Special Power Functions • Most power functions are similar to one of these six • xp with even powers of p are similar to x 2 • xp with negative odd powers of p are similar to x -1 • xp with negative even powers of p are similar to x -2 • Which of the functions have symmetry? § What kind of symmetry?

Polynomials • Definition: § The sum of one or more power function § Each power is a non negative integer

Polynomials • General formula § a 0, a 1, … , an are constant coefficients § n is the degree of the polynomial § Standard form is for descending powers of x § anxn is said to be the “leading term”

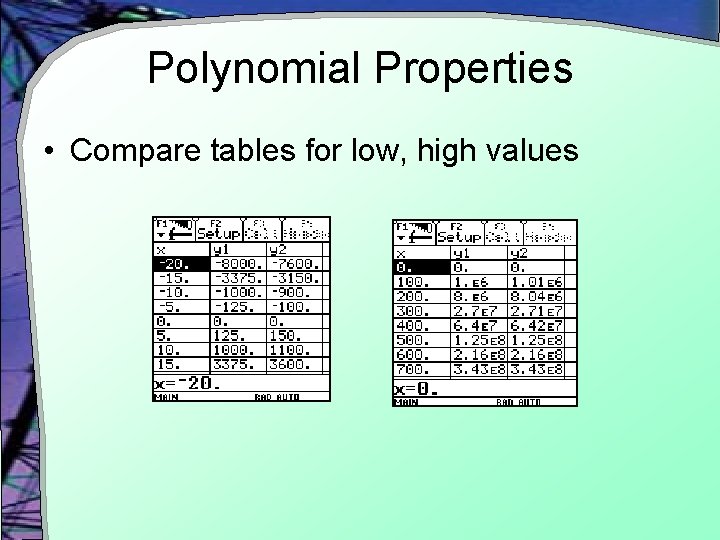
Polynomial Properties • Consider what happens when x gets very large negative or positive § Called “end behavior” § Also “long-run” behavior • Basically the leading term anxn takes over • Compare f(x) = x 3 with g(x) = x 3 + x 2 § Look at tables § Use standard zoom, then zoom out

Polynomial Properties • Compare tables for low, high values

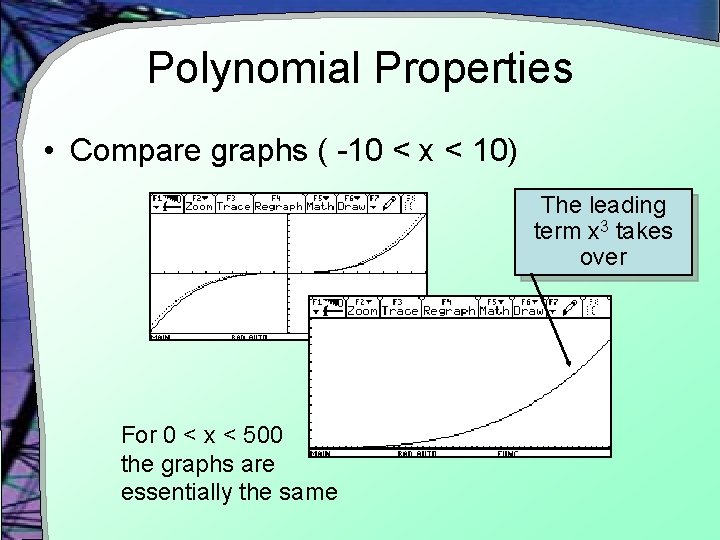
Polynomial Properties • Compare graphs ( -10 < x < 10) The leading term x 3 takes over For 0 < x < 500 the graphs are essentially the same

Zeros of Polynomials • We seek values of x for which p(x) = 0 • We have the quadratic formula • There is a cubic formula, a quartic formula

Zeros of Polynomials • We will use other methods • Consider § What is the end behavior? § What is q(0) = ? § How does this tell us that we can expect at least two roots?

Methods for Finding Zeros • Graph and ask for x-axis intercepts • Use solve(y 1(x)=0, x) • Use zeros(y 1(x), x) • When complex roots exist, use c. Solve() or c. Zeros()

Practice • Given y = (x + 4)(2 x – 3)(5 – x) § What is the degree? § How many terms does it have? § What is the long run behavior? • f(x) = x 3 +x + 1 is invertible (has an inverse) § How can you tell? § Find f(0. 5) and f -1(0. 5)

Assignment • Lesson 9. 2 • Page 400 • Exercises 1 – 29 odd