Polynomial Division Dividing one polynomial by another polynomial

Polynomial Division: Dividing one polynomial by another polynomial to find the zeros of the polynomial. Ex 1: Find the zeros of Solution: 1 st way: At the end of the last section we learned how to solve a third degree polynomial consisting of 4 terms. x = -2, -1, 1 2 nd way: Polynomial Division Since we know we can factor quadratics easily to find the Zeros, we need to be able to divide a higher degree Polynomial so that the remainder ends up being a quadratic. Since this example is of degree three, we need a polynomial of degree one as a divisor.

We are not “given” any zeros of the function that we can turn into factors, so we have to try and find one. Start by substituting in integers into the polynomial to see if it simplifies to zero – for this example we only need one! By inspection, P(1)=0, therefore, we turn it into a factor: x - 1 x – 1 becomes our divisor. NOTE: your polynomial must have a place reserved for every degree in decreasing order. If a term is missing you insert one with coefficient of zero. Now divide by asking: How many times does “x” go into x 3? Place your answer in the top. 2 x - 2 -(2 x – 2) 0 Multiply your first answer by the divisor and subtract that product from your polynomial. Repeat the process until you cannot divide anymore Note: For now, you may not always get a zero as a remainder!

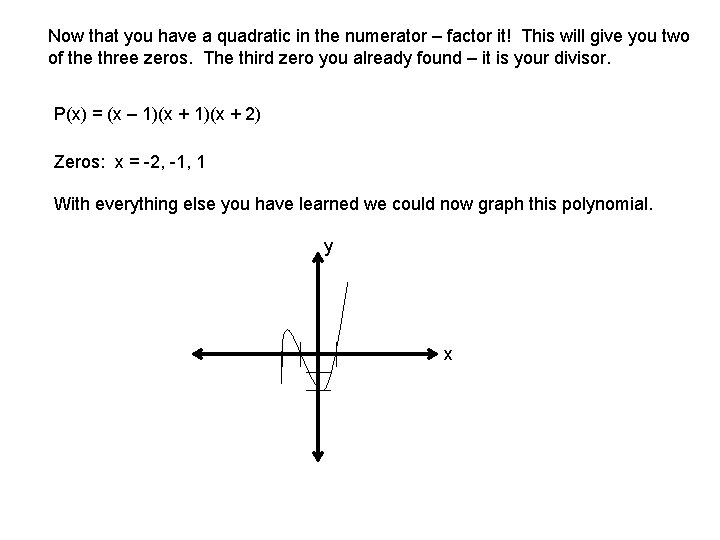
Now that you have a quadratic in the numerator – factor it! This will give you two of the three zeros. The third zero you already found – it is your divisor. P(x) = (x – 1)(x + 2) Zeros: x = -2, -1, 1 With everything else you have learned we could now graph this polynomial. y x

Division Algorithm: Suppose D(x) and P(x) are polynomials with D(x)≠ 0 and the degree of d(x) is Less than the degree of P(x). Then there exist unique polynomials Q(x) and R(x), Where R(x) is either 0 or has a degree less than D(x), such that P(x) = Q(x) ∙ D(x) + R(x) or, equivalently, Ex 2: Find the quotient and remainder when the polynomial is divided by the polynomial Solution: Note: The degree of 2 is missing from P(x). You must insert Now do polynomial division as in the last example. This time we do not need to find any zeros of our own because all they ask us to do is divide – they do not ask us to find zeros.

Ex: Find all the rational numbers that are possibilities for zeros of the polynomial If your polynomial has coefficients that are not integers – make them integers! Q: What is the smallest denominator that could we multiply by to eliminate all fractions at once? A: 4; since 4 is a multiple of 2 it will eliminate it as well. The rational zero test is performed by taking the factors of your constant and Divide them by the factors of your leading coefficient. Constant: -2 Leading coefficient: 4

Now divide all of these factors: We see that there are 8 possibilities for rational zeros Recall: Rational numbers can be put in the form of p/q. Irrational numbers cannot, and WOULD NOT be present in this list if any exist. The rational zero test limits the number of possibilities from infinitely many to just a few. Since this is a cubic function we can have anywhere from 1 to 3 zeros, some may be rational some may be irrational and some may be repeated. After finding which possibilities for zeros actually are zeros you would perform the division algorithm as before.

Solution: x = Think Pair Share: Given find all possibilities for rational roots, find all rational and irrational roots, and graph the polynomial. The factors used for the divisor are: x +2 x– 3 2 x – 1 Since this is a combination of linear factors R(x) must be 0.

Is not factorable for obtaining “real” zeros, meaning there are no other zeros – there are repeated zeros. The power of two in this quadratic tells you that none of the original three zeros are repeated. They all total 5.