11 3 Rational Functions and Their Graphs Rational

§ 11. 3 Rational Functions and Their Graphs

Rational Expressions A rational expression consists of a polynomial divided by a nonzero polynomial (denominator cannot be equal to 0). A rational function is a function defined by a formula that is a rational expression. For example, the following is a rational function: Blitzer, Algebra for College Students, 6 e – Slide #2 Section 11. 3

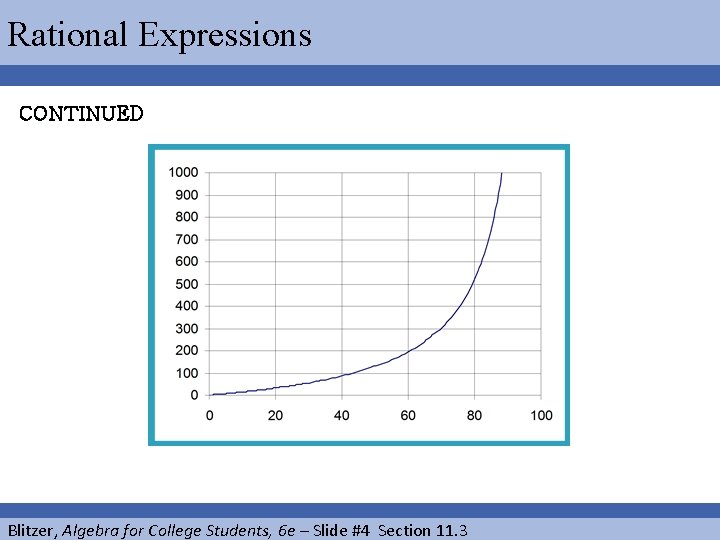
Rational Expressions EXAMPLE The rational function models the cost, f (x) in millions of dollars, to inoculate x% of the population against a particular strain of flu. The graph of the rational function is shown. Use the function’s equation to solve the following problem. Find and interpret f (60). Identify your solution as a point on the graph. Blitzer, Algebra for College Students, 6 e – Slide #3 Section 11. 3

Rational Expressions CONTINUED Blitzer, Algebra for College Students, 6 e – Slide #4 Section 11. 3

Rational Expressions CONTINUED SOLUTION We use substitution to evaluate a rational function, just as we did to evaluate other functions. This is the given rational function. Replace each occurrence of x with 60. Perform the indicated operations. Blitzer, Algebra for College Students, 6 e – Slide #5 Section 11. 3

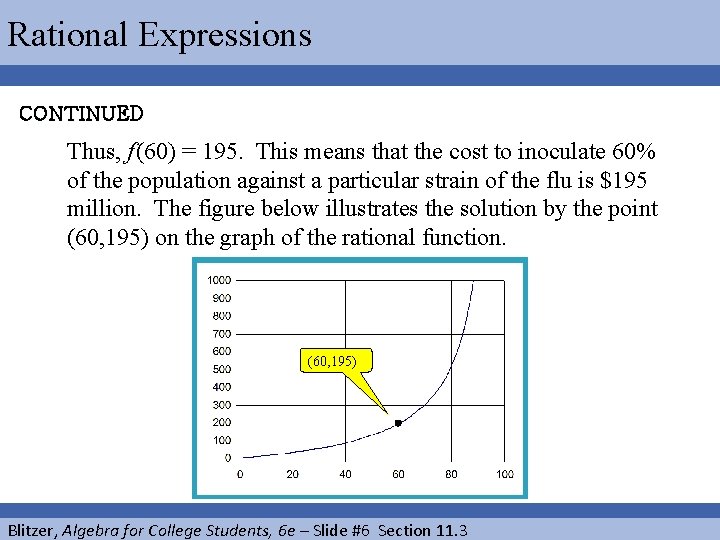
Rational Expressions CONTINUED Thus, f (60) = 195. This means that the cost to inoculate 60% of the population against a particular strain of the flu is $195 million. The figure below illustrates the solution by the point (60, 195) on the graph of the rational function. (60, 195) Blitzer, Algebra for College Students, 6 e – Slide #6 Section 11. 3

Rational Functions - Domain EXAMPLE Find the domain of f if SOLUTION The domain of f is the set of all real numbers except those for which the denominator is zero. We can identify such numbers by setting the denominator equal to zero and solving for x. Set the denominator equal to 0. Factor. Blitzer, Algebra for College Students, 6 e – Slide #7 Section 11. 3

Rational Functions - Domain CONTINUED or Set each factor equal to 0. Solve the resulting equations. Because 4 and 9 make the denominator zero, these are the values to exclude. Thus, or Blitzer, Algebra for College Students, 6 e – Slide #8 Section 11. 3

Rational Functions - Domain CONTINUED In this example, we excluded 4 and 9 from the domain. Unlike the graph of a polynomial which is continuous, this graph has two breaks in it – one at each of the excluded values. Since x cannot be 4 or 9, there is not a function value corresponding to either of those x values. At 4 and at 9, there will be dashed vertical lines called vertical asymptotes. The graph of the function will approach these vertical lines on each side as the x values draw closer and closer to each of them, but will not touch (cross) the vertical lines. The lines x = 4 and x = 9 each represent vertical asymptotes for this particular function. Blitzer, Algebra for College Students, 6 e – Slide #9 Section 11. 3

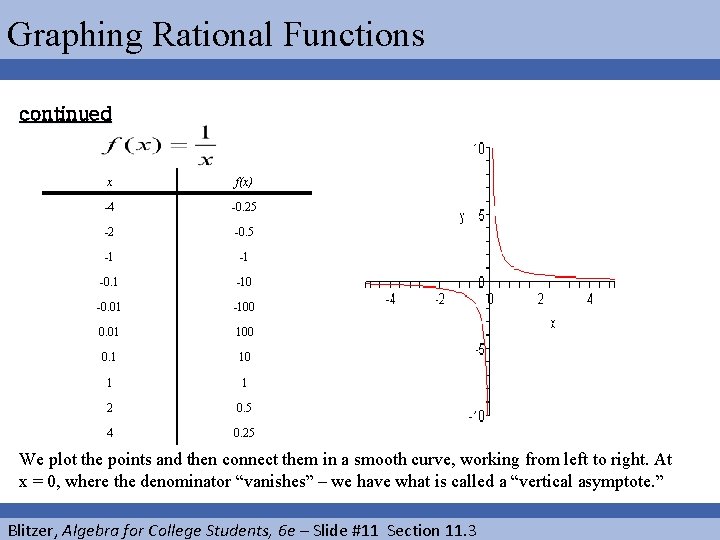
Graphing Rational Functions EXAMPLE Sketch the graph of the rational function: The first thing we notice is that x cannot be 0, for that value of x would make the denominator 0, and 0 denominators are not allowed. With rational functions, at any x value that would make the denominator equal to 0, we either get a hole in the graph or we get a vertical asymptote. On this first example, we’ll just plug in some values for x and see what we get for y or f(x). It looks like that when x is positive , f(x) is positive in this example. When x is negative, f(x) is also negative. Also, when x gets closer and closer to 0 coming from the positive side, f(x) gets bigger and bigger. Let’s get enough points now to see what the graph might look like. Blitzer, Algebra for College Students, 6 e – Slide #10 Section 11. 3

Graphing Rational Functions continued x f(x) -4 -0. 25 -2 -0. 5 -1 -1 -0. 1 -10 -0. 01 -100 0. 01 100 0. 1 10 1 1 2 0. 5 4 0. 25 We plot the points and then connect them in a smooth curve, working from left to right. At x = 0, where the denominator “vanishes” – we have what is called a “vertical asymptote. ” Blitzer, Algebra for College Students, 6 e – Slide #11 Section 11. 3

Graphing Rational Functions continued You should notice that this graph is made up of two separate pieces. Almost all rational functions have graphs that are in multiple pieces. Notice that there is no x intercept and no y intercept. Remember that y intercepts occur when x = 0 and x cannot be 0 in this example. X intercepts occur when y = 0. A rational function will be 0 when its numerator is 0 and in this example, the numerator is 1 and thus cannot be equal to 0. Blitzer, Algebra for College Students, 6 e – Slide #12 Section 11. 3

Asymptotes In graphing rational functions, it is most important to consider the asymptotes for the function. Asymptotes Vertical Asymptotes A vertical line that the graph of a function approaches, but does not touch. Horizontal Asymptotes A horizontal line that the graph of a function approaches as x gets very large or very small. The graph of a function may touch/cross its horizontal asymptote. Blitzer, Algebra for College Students, 6 e – Slide #13 Section 11. 3

Graphing Rational Functions We started with a very easy graphing example. Graphing rational functions can sometimes be very difficult. There are some things you should look at when graphing a rational function: Any vertical asymptotes? These will occur where the denominator vanishes, or is equal to 0 with no corresponding factor in the numerator to cancel the factor out (that is, in reduced form the problem factor is still in the denominator). The graph won’t cross a vertical asymptote. You may have several vertical asymptotes. Any horizontal asymptotes? This is what happens on the edges of the graph. Is there a number that f(x) will approach as x gets larger and larger, or as x gets smaller and smaller? Horizontal asymptotes will be indicated by dotted lines that go across the graph. The graph sometimes crosses the horizontal asymptote. Blitzer, Algebra for College Students, 6 e – Slide #14 Section 11. 3

Graphing Rational Functions Any x intercepts? Reduce the rational expression to lowest terms first. If there are values that make the numerator zero, they will make the whole expression 0 and thus they are your x intercepts. A y intercept? Set x = 0. If you get a value for y, then that is your y intercept. If you have a y intercept, you will have only one. Remember that we are looking at functions and for each x, there is only one y. Any symmetry? Sometimes we will see that, for example, substitution of +x and –x into the function produces the same y value. In that case, we know that the LHS of the graph looks just like the RHS and we have symmetry about the y axis. We could fold the graph on the y axis and one part would fall on top of the other. If f(-x) = f(x), we have y axis symmetry. Another symmetry that might exist is origin symmetry. If f(-x) is the opposite of f(x), we have origin symmetry. That is, if f(-x) = -f(x) we have symmetry with respect to the origin. If we folded the graph on the x axis and then again on the y, one part of the graph would fall on top of the other when we have origin symmetry. Blitzer, Algebra for College Students, 6 e – Slide #15 Section 11. 3

Graphing Rational Functions After looking at intercepts, asymptotes and symmetry – it’s time to just plot a few points. You should plot at least one point between and beyond each x-intercept and vertical asymptote. Hint for horizontal asymptotes… Look at the degree of the numerator and the degree of the denominator. If the degree of the numerator is higher, the numerator dominates and you have no horizontal asymptote. If the degree of the denominator is higher, the horizontal asymptote is y = 0 or the x-axis. If the degree of the numerator is equal to the degree of the denominator, your horizontal asymptote is the ratio of coefficients of leading terms. These facts can be proved using calculus. There is much to remember when graphing rational functions, but maybe some of this will come together for you when we look at some examples. And now…. We will get started with graphing rational functions. Blitzer, Algebra for College Students, 6 e – Slide #16 Section 11. 3

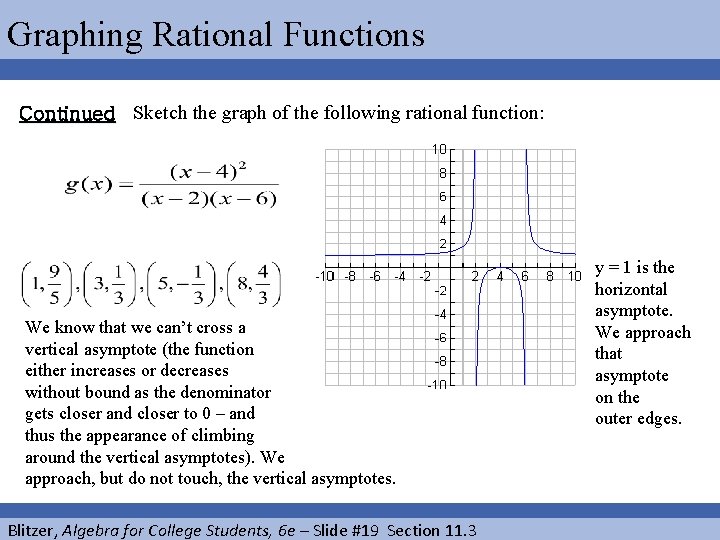
Graphing Rational Functions EXAMPLE Sketch the graph of the following rational function: We note that this rational expression is already reduced to lowest terms. In this form we can see several things. There are two vertical asymptotes. They occur at x = 2 and at x = 6, for the denominator is 0 at each of those values. The numerator is 0 when x = 4, and so we have an x intercept at (4, 0). We only have one x intercept in this example, although we sometimes have more than one x intercept. When we substitute 0 for x, we get (0, intercept. ) which is (0, Blitzer, Algebra for College Students, 6 e – Slide #17 Section 11. 3 ). That is our y

Graphing Rational Functions Continued Sketch the graph of the following rational function: The degree of the numerator is 2 and the degree of the denominator is 2. That means we have a horizontal asymptote of y equal to the ratio of leading coefficients of numerator and denominator. The leading coefficient in the numerator is just 1 and that is also the leading coefficient in the denominator. Then y = 1/1 is the horizontal asymptote. The graph will approach that line on the outer edges. Some important x values for us in this example are 2, 4, 6. We should plot some points around these important x values. Let’s pick x = 1, x = 3, x = 5, x = 8 to plot. We substitute these values for x into our equation and we get these values: Blitzer, Algebra for College Students, 6 e – Slide #18 Section 11. 3

Graphing Rational Functions Continued Sketch the graph of the following rational function: We know that we can’t cross a vertical asymptote (the function either increases or decreases without bound as the denominator gets closer and closer to 0 – and thus the appearance of climbing around the vertical asymptotes). We approach, but do not touch, the vertical asymptotes. Blitzer, Algebra for College Students, 6 e – Slide #19 Section 11. 3 y = 1 is the horizontal asymptote. We approach that asymptote on the outer edges.

Graphing Rational Functions EXAMPLE Sketch the graph of the following rational function: We first verify that the expression is reduced to lowest terms, and it is. Then we look at vertical asymptotes. There is one at x = 0. We now notice that the degree of the numerator is 2 and the degree of the denominator is also 2. That means that we have a horizontal asymptote at the ratio of coefficients of the leading terms, or at y = since the highest degree term in the numerator has a coefficient of 4 and the highest degree term in the denominator has a coefficient of 3. Blitzer, Algebra for College Students, 6 e – Slide #20 Section 11. 3

Graphing Rational Functions Continued Sketch the graph of the following rational function: We see that the numerator factors into (2 x+ 3)(2 x – 3) and it has roots of Then we have two x intercepts and they are at ( , 0) and ( and , 0) We try to substitute x = 0 into the equation and get that the function value is undefined there. We then remember that x= 0 is our vertical asymptote. We have no y intercepts then, for y doesn’t exist when x = 0. We can see that we have only even powered terms in our function and that means that x and (-x) would produce the same y value. Then we have symmetry with respect to the y axis and the left hand part of the graph will look just like the right hand part. Blitzer, Algebra for College Students, 6 e – Slide #21 Section 11. 3

Graphing Rational Functions Continued Sketch the graph of the following rational function: Now, having noted all these things, it’s time to just plot a few points. Our important x values for this example were Those three points divide our x axis into four parts and it’s important to pick at least one point from each part to graph. Let’s pick nice numbers that are not too far away from our values. Let’s pick… -2, -1, 1, 2. We substitute and get the following points on our graph: Blitzer, Algebra for College Students, 6 e – Slide #22 Section 11. 3

Graphing Rational Functions Continued Sketch the graph of the following rational function: and x-intercepts We plot these six points and then connect the dots, working from left to right, connecting in a smooth curve. We must remember to crawl to our horizontal asymptote of y = 4/3 on the sides, and “go to infinity” (or negative infinity in this case) around our vertical asymptote of x = 0. Blitzer, Algebra for College Students, 6 e – Slide #23 Section 11. 3

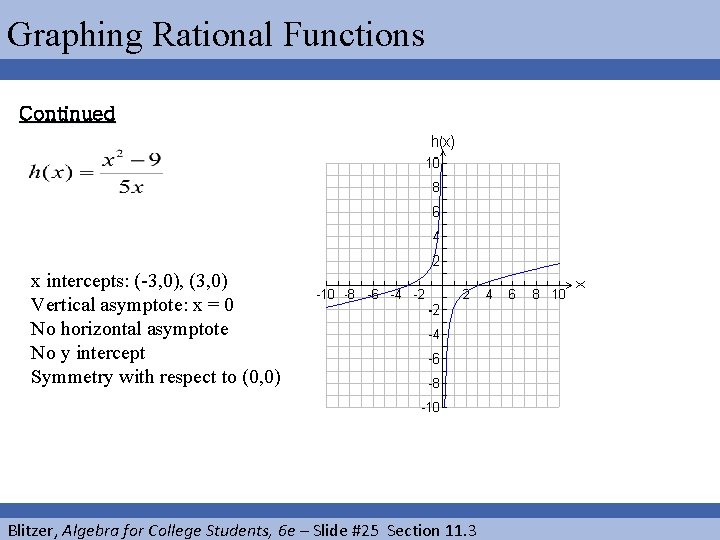
Graphing Rational Functions EXAMPLE Consider the following rational function and determine everything you can by looking at the original expression. Then put all your facts together to sketch the graph. Do you see the x-intercepts of plus and minus 3? Do you see that there is no yintercept and do you know why? Do you see that there is no horizontal asymptote? Do you see the symmetry with respect to the origin? If yes, you are on your way to understanding the basics of graphing rational functions. The graph for this function is provided on the next slide. Blitzer, Algebra for College Students, 6 e – Slide #24 Section 11. 3

Graphing Rational Functions Continued x intercepts: (-3, 0), (3, 0) Vertical asymptote: x = 0 No horizontal asymptote No y intercept Symmetry with respect to (0, 0) Blitzer, Algebra for College Students, 6 e – Slide #25 Section 11. 3

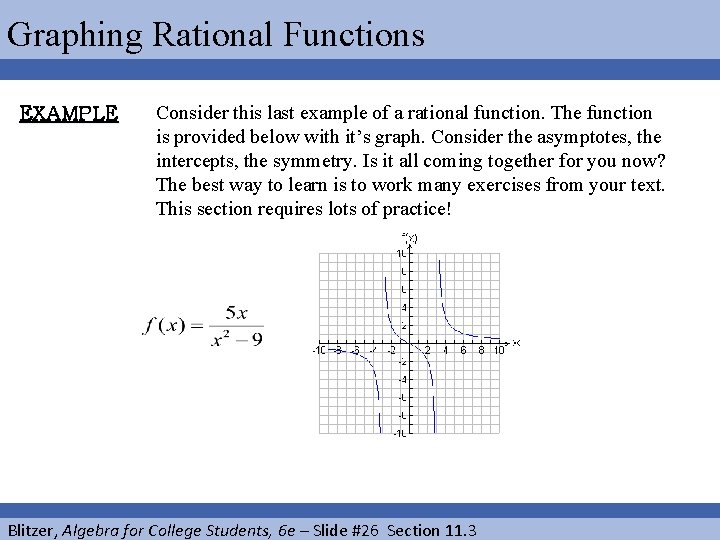
Graphing Rational Functions EXAMPLE Consider this last example of a rational function. The function is provided below with it’s graph. Consider the asymptotes, the intercepts, the symmetry. Is it all coming together for you now? The best way to learn is to work many exercises from your text. This section requires lots of practice! Blitzer, Algebra for College Students, 6 e – Slide #26 Section 11. 3