3 6 Graphs of Rational Functions A rational

3. 6 Graphs of Rational Functions

• A rational function is a quotient of two polynomial functions.

Parent function: has branches in 1 st and 3 rd quadrants. No x or y -intercepts. Branches approach asymptotes.

Vertical asymptote – the line x = a is a VA for f(x) if f(x) approaches infinity or f(x) approaches negative infinity as x approaches a from either the left or the right. The VA is where the function is undefined or the value(s) that make the denominator = 0. • Whenever the numerator and denominator have a common linear factor, a point discontinuity may appear. If, after dividing the common linear factors, the same factor remains in the denominator, a VA exists. Otherwise the graph will have point discontinuity. That means there is a hole in the Asymptote graph at that point and not an asymptote Hole

Ex 1 find any VA or holes

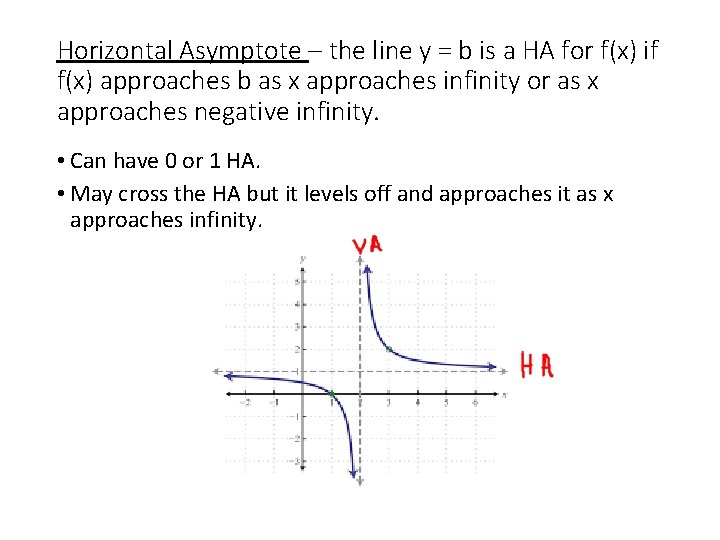
Horizontal Asymptote – the line y = b is a HA for f(x) if f(x) approaches b as x approaches infinity or as x approaches negative infinity. • Can have 0 or 1 HA. • May cross the HA but it levels off and approaches it as x approaches infinity.

Shortcut for HA’s • If the degree of the denominator is > the degree of the numerator then there is a HA at y = 0. • If the degree of the numerator is > the degree of the denominator then there is NO HA. • If the degree of the numerator = the degree of the denominator then the HA is y = a/b where a is the leading coefficient of the numerator & b is the LC of the denominator.

Determine the asymptotes & the x and yintercepts Degrees are equal a/b

Find asymptotes, x-int, y-int Degree is bigger in the denominator y=0

find asymptotes Degree is bigger in the denominator y=0 Degrees are equal y=a/b

Slant asymptote • There is an oblique or slant asymptote if the degree of P(x) is EXACTLY one degree higher than Q(x). • If this is the case the oblique asymptote is the quotient part of the division. • Can have 0 or 1 slant asymptote. • Can have a VA and slant, a HA and VA, but NOT a HA and slant. Either it has a slant or is has a HA

find the slant asymptote Degree is exactly one bigger in the numerator divide

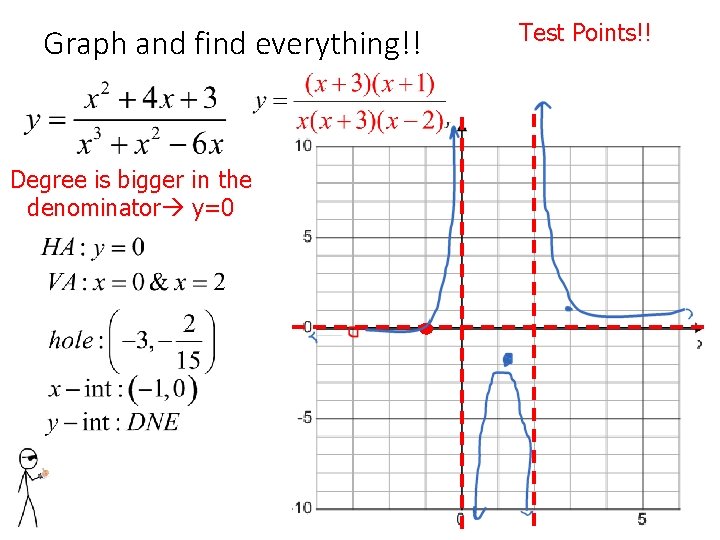
Graph and find everything!! Degree is bigger in the denominator y=0 Test Points!!

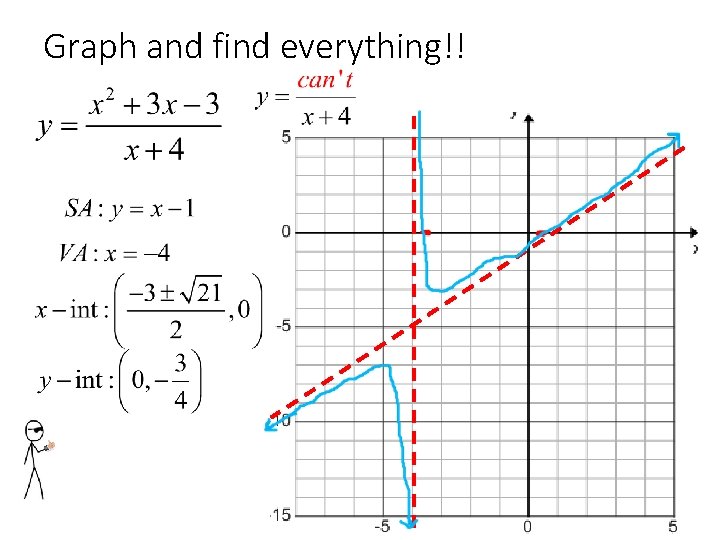
Graph and find everything!!

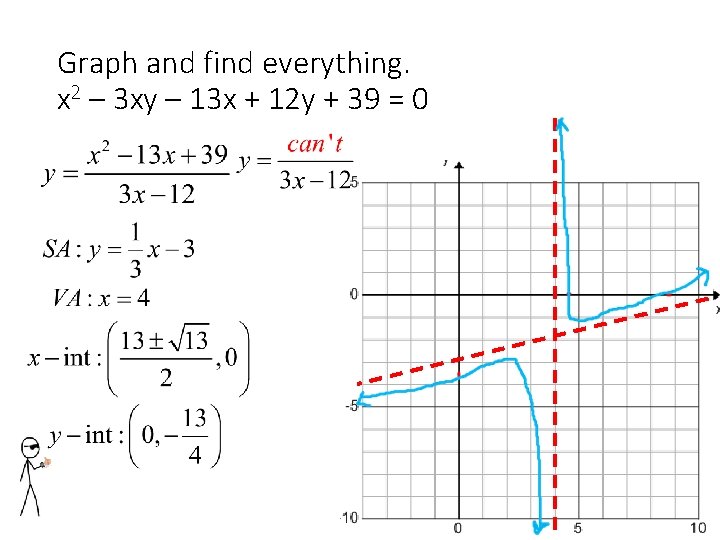
Graph and find everything. x 2 – 3 xy – 13 x + 12 y + 39 = 0

Homework pg 313 #5 -9 odd, 15 -23 odd, 33 -39 odd, 59, 63