Rational Functions and Their Graphs n r a












- Slides: 16

Rational Functions and Their Graphs n r a e l l l ’ u yo t a h W To identify properties of rational functions. To graph rational functions. y r a bul a c o V Rational function, continuous graph, discontinuous graph, point of discontinuity, Removable discontinuity, non removable discontinuity

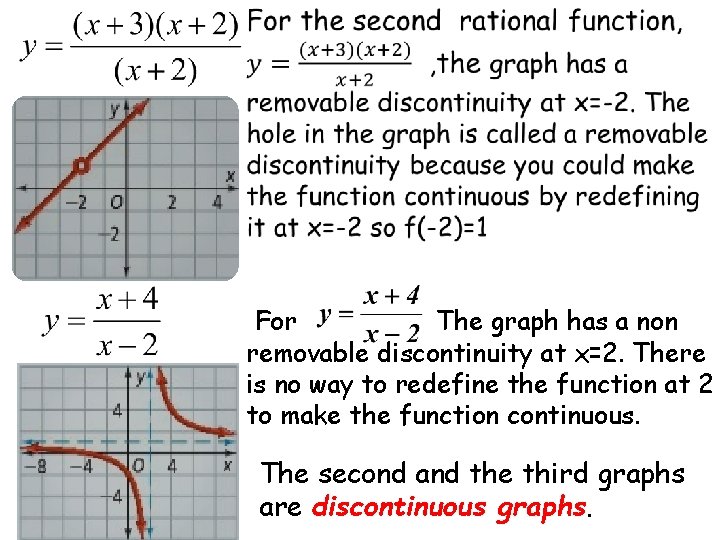
Here are graphs of three rational functions

For The graph has a non removable discontinuity at x=2. There is no way to redefine the function at 2 to make the function continuous. The second and the third graphs are discontinuous graphs.

Take Note: Key Concept Point of Discontinuity .


Problem 1: Finding Points of Discontinuity What are the domain and points of discontinuity of each rational functions? Are the points of discontinuity removable or non- removable? What are the x- and y-intercept? Factor numerator and denominator to check for common factors. To find the y- intercept, let x=0 and simplify.

You can not factor the numerator or the denominator. Also, there are not values of x that make the denominator 0. The domain of the function is all real numbers, and there are no discontinuities. To find the y- intercept, let x=0 and simplify.

Factor numerator and denominator.

Your Turn What are the domain and points of discontinuity of each rational functions? Are the points of discontinuity removable or non- removable? What are the x- and y-intercept? Domain: all real numbers except x=4 and x=-4 Points of discontinuity: (non removable) x=4 and x=-4 X intercept: NO Y intercept: Answers Domain: all real numbers. Points of discontinuity: NO X intercept: (1, 0) Y intercept: Domain: all real numbers except x=-2 and x=-1 Points of discontinuity: (non removable) x=-2 and removable at x=-1 X intercept: x=-1 Y intercept:

Take a note: Vertical Asymptotes

Problem 2: Finding Vertical Asymptotes Answer Your turn Since 2 and 3 are zeros of the denominator and neither is zero of the numerator, the lines x= 2 and x = 3 are vertical asymptotes. Answers

Take a note: Horizontal asymptote of a Rational Function To find the horizontal asymptote of the graph of a rational function, compare the degree of the numerator m to the degree of the denominator n. If m<n, the graph has an horizontal asymptote y=0 (the x-axis) If m>n, the graph has no horizontal asymptote If m=n, the graph has horizontal asymptote where a is the coefficient of the term of the greatest degree in the numerator and b is the coefficient of the term of the greatest degree in the denominator.

Problem 3 Finding Horizontal Asymptotes What is the Horizontal asymptote for the rational function? Answers The degree of the numerator is less than the degree of the The degree of the numerator The numerator is greater than the degree of and the denominator. have the same degree. No Horizontal Asymptote Take a note: You can get a reasonable graph for a rational function by finding all intercepts and asymptotes. Some times you will also have to plot a few points to get a good sense of the shape of the graph.

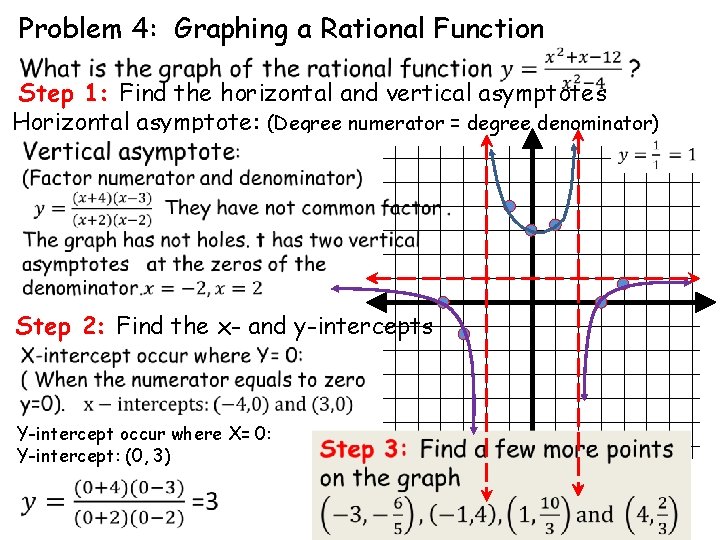
Problem 4: Graphing a Rational Function Step 1: Find the horizontal and vertical asymptotes Horizontal asymptote: (Degree numerator = degree denominator) Step 2: Find the x- and y-intercepts Y-intercept occur where X= 0: Y-intercept: (0, 3)

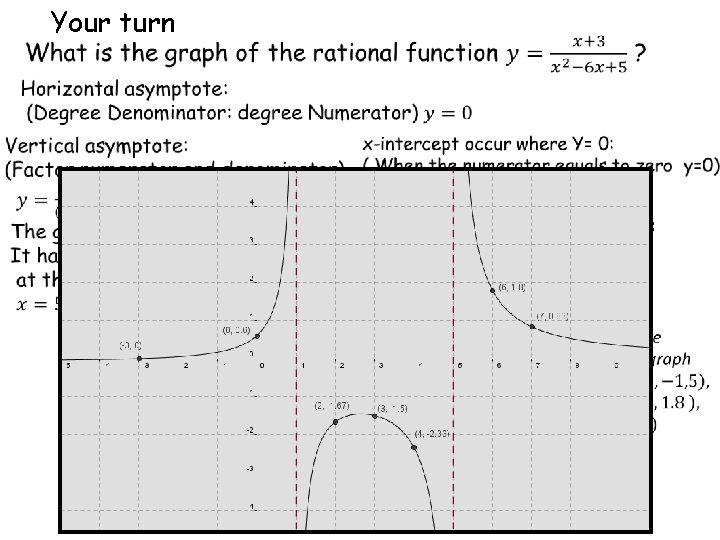
Your turn y-intercept occur where X= 0:

Classwork odd TB pg. 521 Ex. 13 -34 Homework even