Unit 6 Radical and Rational Functions Roots and






































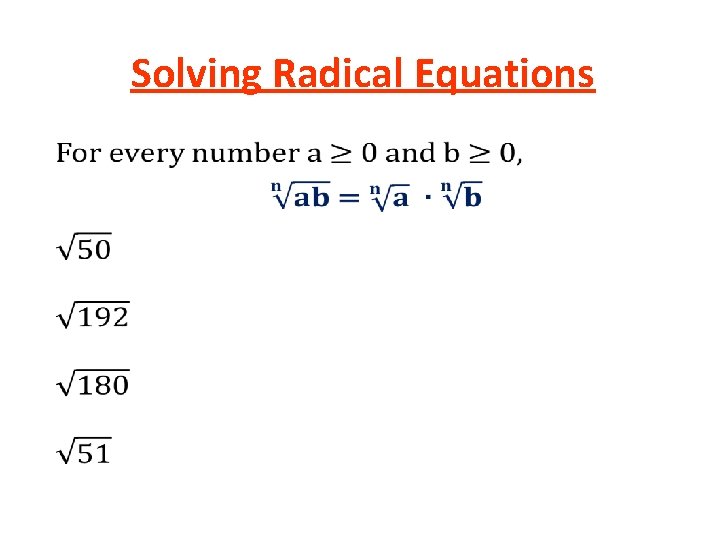














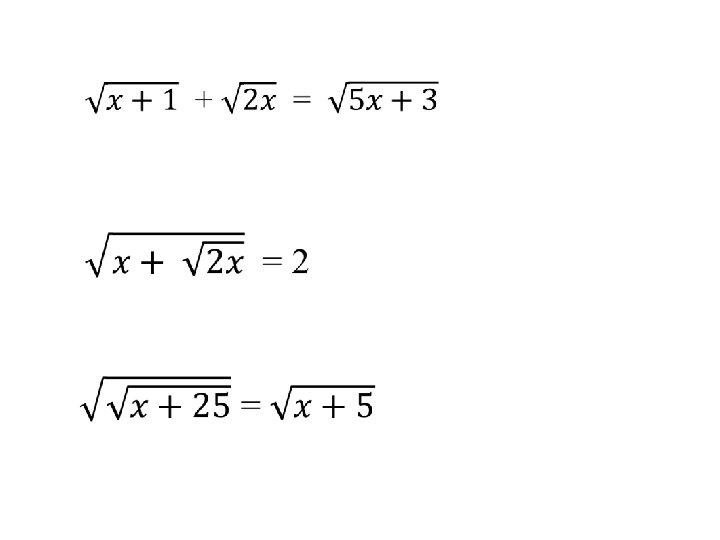








- Slides: 70

Unit 6: “Radical and Rational Functions” Roots and Radical Expressions Objective: To evaluate and simplify radical expressions. nth root – For any real number a, b, and positive integer n, if an = b, then “a is the nth root of b”. Example: Since 43 = 64, then “ 4 is the 3 rd root of 64” v. A radical is used to indicate a root.

Evaluating Radicals •

Simplifying Radicals • 1 4 9 16 25 36 49 64 81 100 121 144

Simplifying Radicals •

Simplifying Radicals with Variables •

Simplifying Radicals with Variables •

Multiply Two Radicals •

Multiply Two Radicals •

Dividing Two Radicals

Rationalizing the Denominator

End of Day 1 P 366 #13 – 16, #39 – 46 P 371 #17 - 22

Adding and Subtracting Two Radicals In order to add or subtract two radical expression they must be LIKE RADICALS. Like radicals have the same index and same radicand.

Adding Radicals

Subtracting Radicals

Multiplying Binomial Radicals

Rationalizing Binomial Denominators

P 377 #28 – 44 evens

Factoring Quadratic Expressions Objective: To find common factors and binomial factors of quadratic expressions. factor – if two or more polynomials are multiplied together, then each polynomial is a factor of the product. (2 x + 7)(3 x – 5) = 6 x 2 + 11 x – 35 FACTORS PRODUCT (2 x – 5)(3 x + 7) = 6 x 2 – x – 35 FACTORS PRODUCT “factoring a polynomial” – reverses the multiplication!

Finding Greatest Common Factor greatest common factor (GCF) – the greatest of the common factors of two or more monomials.


Finding Binomial Factors

Finding Binomial Factors

Finding Binomial Factors

Finding Binomial Factors

Finding Binomial Factors

Finding Binomial Factors

Factoring Special Expressions*

Solving Quadratics Equations: Factoring and Square Roots Objective: To solve quadratic equations by factoring and by finding the square root.

Solve by Factoring

Solve by Factoring

Solve by Factoring*

Solve by Factoring*

Solve Using Square Roots •

Solve Using Square Roots

Solve Using Square Roots*

Math 2 Assignment pp. 259 -260 #7 -21 odd, 35 -45 odd p. 266 #1 -19 odd End of Day 3

Solving Radical Equations •

Solving Radical Equations •
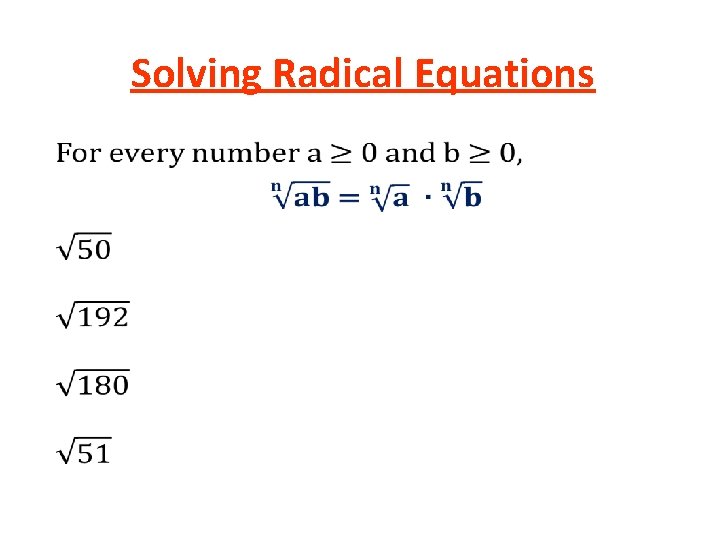
Solving Radical Equations •

Solving Radical Equations •

Solving Radical Equations •

Solving Radical Equations •

Solving Radical Equations •

Solving Radical Equations •

Solving Radical Equations •

Solving Radical Equations •

Solving Radical Equations •

Solving Radical Equations* •

Solving Radical Equations* •

Solving Radical Equations* •

Solving Radical Equations* •

Solving Radical Equations* •

P 388 # 2 -12 evens, 15 -18, 25, 26, 28, 30 End of Day 2
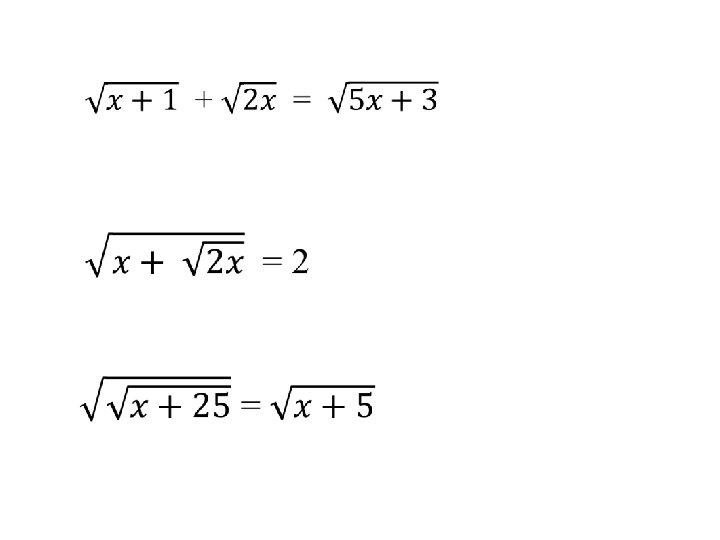

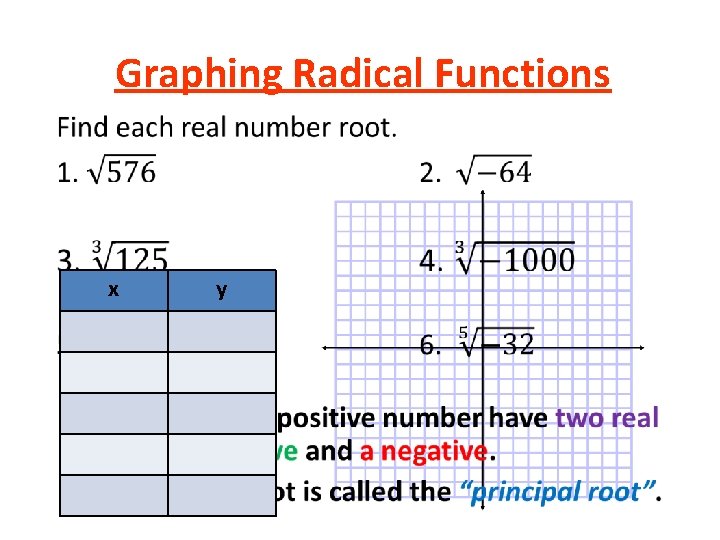
Graphing Radical Functions • x y

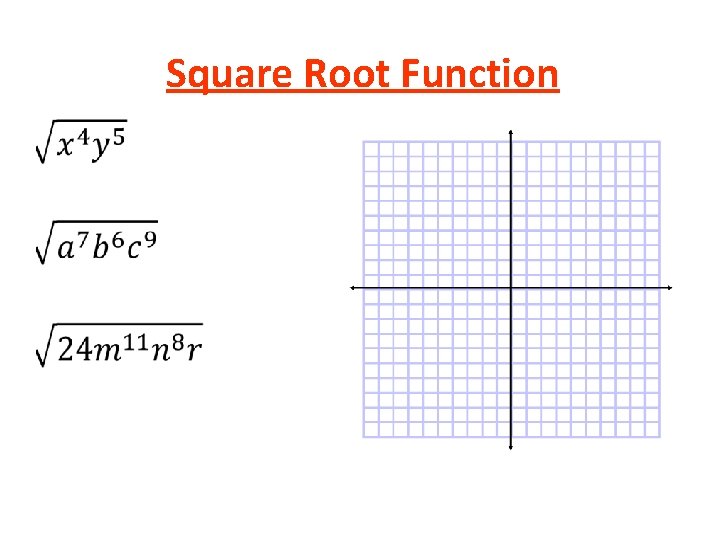
Square Root Function •

Square Root Function •

Square Root Function •

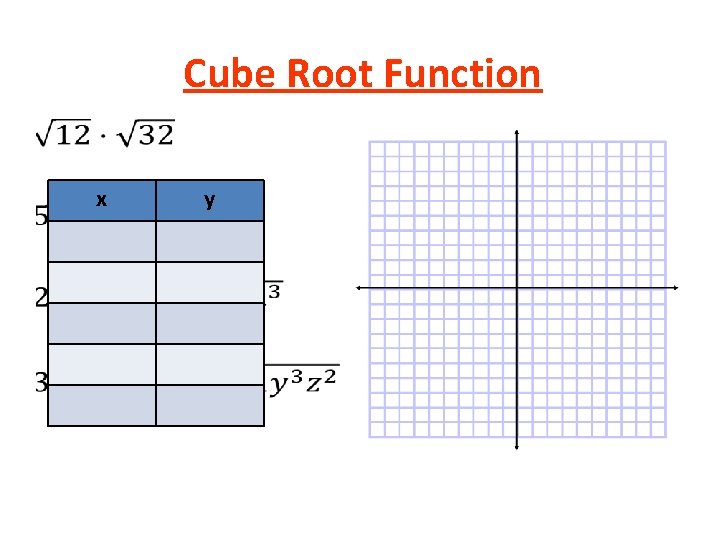
Cube Root Function • x y

Cube Root Function •

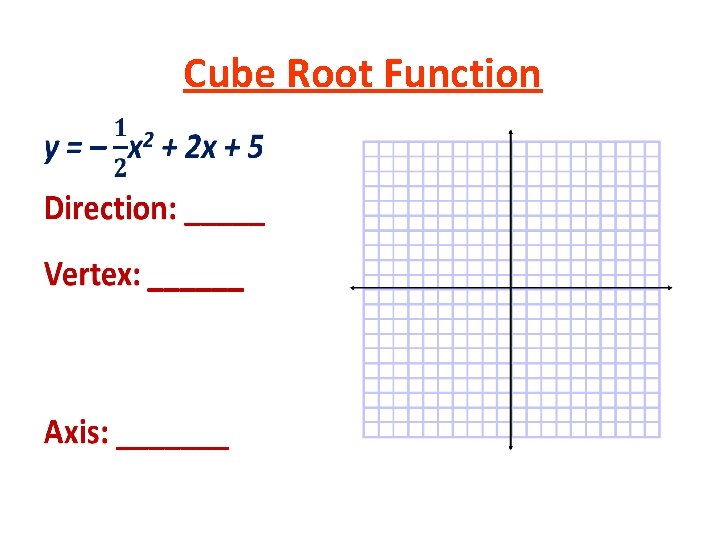
Cube Root Function •

Cube Root Function •

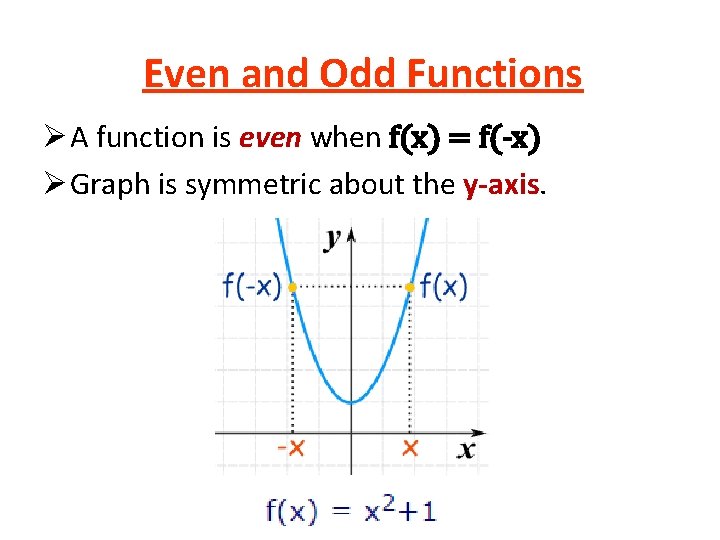
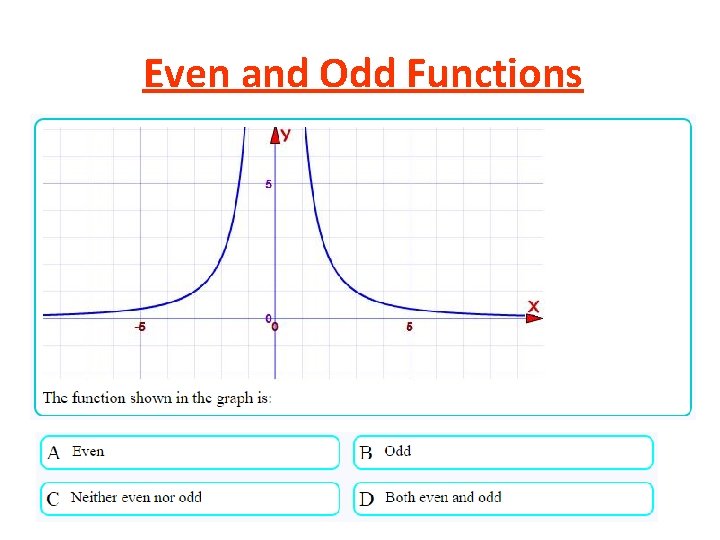
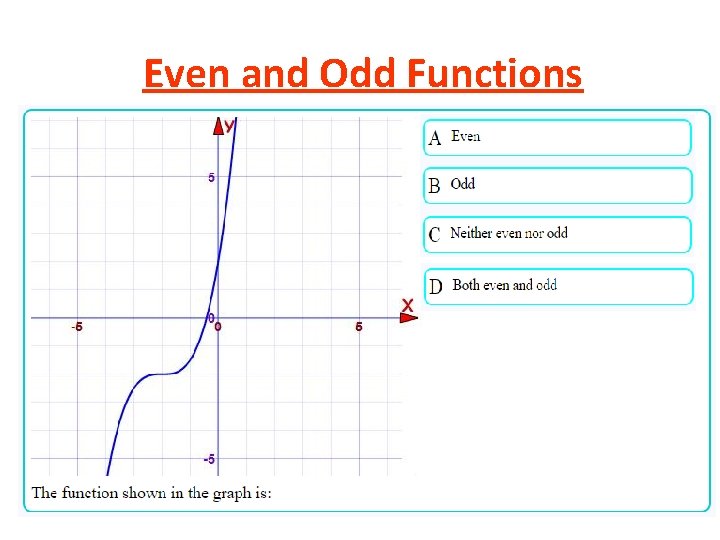
Even and Odd Functions Ø A function is even when f(x) = f(-x) Ø Graph is symmetric about the y-axis.

Even and Odd Functions Ø A function is odd when -f(x) = f(-x) Ø Graph is symmetric about the origin (180° Rot).

Even and Odd Functions

Even and Odd Functions

Even and Odd Functions

Even and Odd Functions

Cube Root Function •

End of day 3 P 411 #17 -21, 24 -28