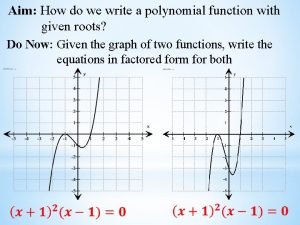
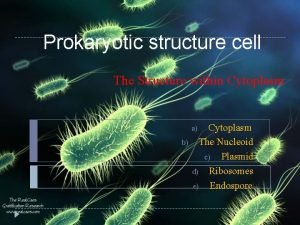
7 1 IntroductionFunctions and Inverses A function is















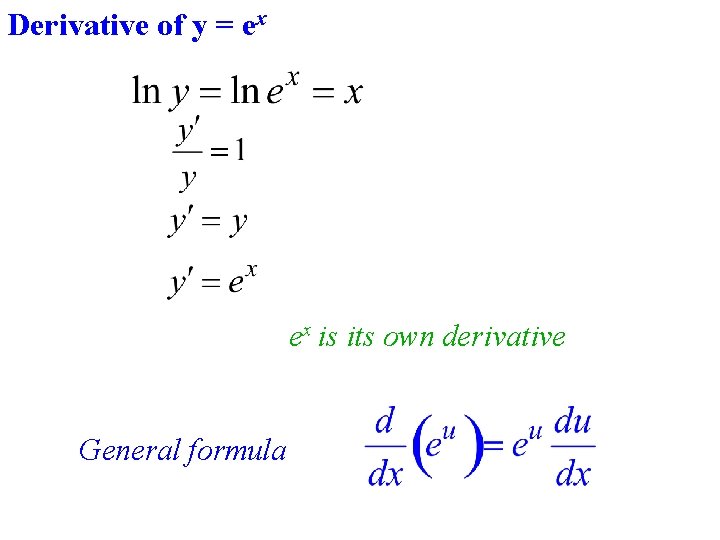
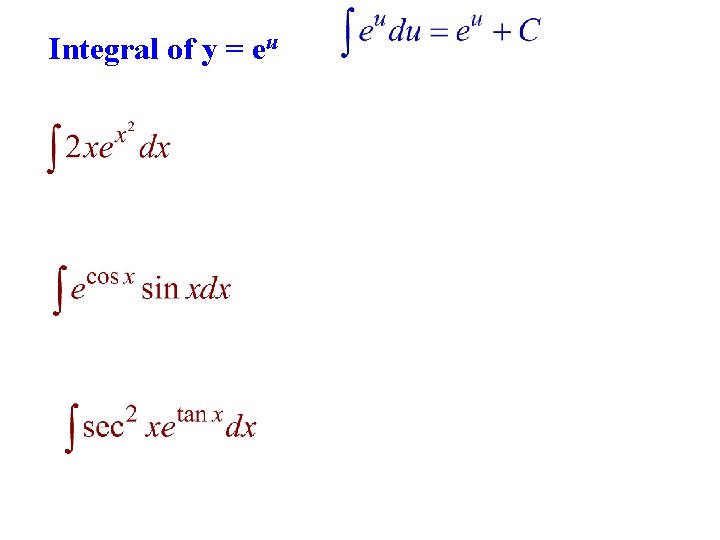
































- Slides: 63

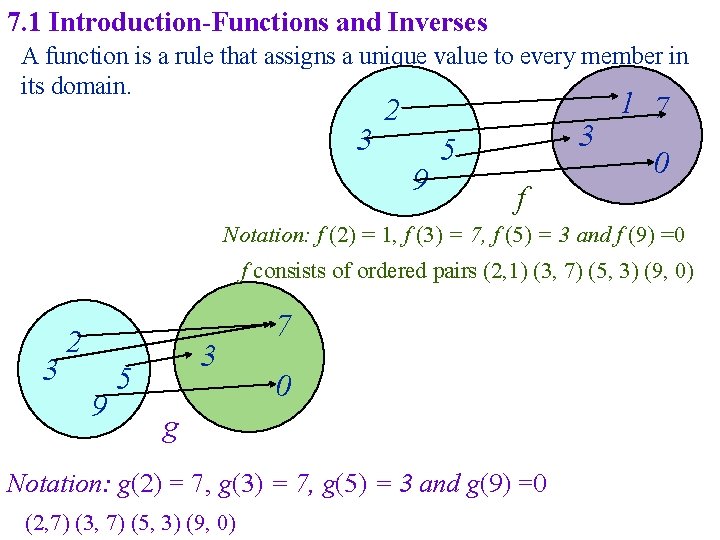
7. 1 Introduction-Functions and Inverses A function is a rule that assigns a unique value to every member in its domain. 3 2 9 3 5 1 7 0 f Notation: f (2) = 1, f (3) = 7, f (5) = 3 and f (9) =0 f consists of ordered pairs (2, 1) (3, 7) (5, 3) (9, 0) 3 2 9 3 5 7 0 g Notation: g(2) = 7, g(3) = 7, g(5) = 3 and g(9) =0 (2, 7) (3, 7) (5, 3) (9, 0)

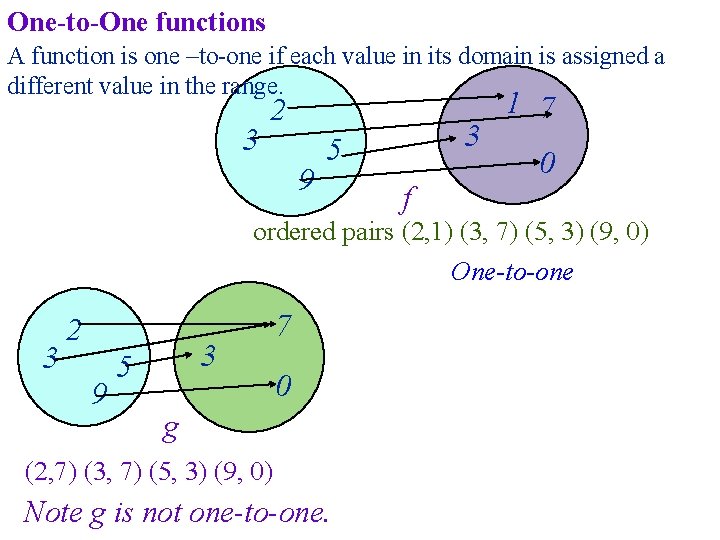
One-to-One functions A function is one –to-one if each value in its domain is assigned a different value in the range. 3 2 9 3 5 1 7 0 f ordered pairs (2, 1) (3, 7) (5, 3) (9, 0) One-to-one 3 2 9 3 5 7 0 g (2, 7) (3, 7) (5, 3) (9, 0) Note g is not one-to-one.

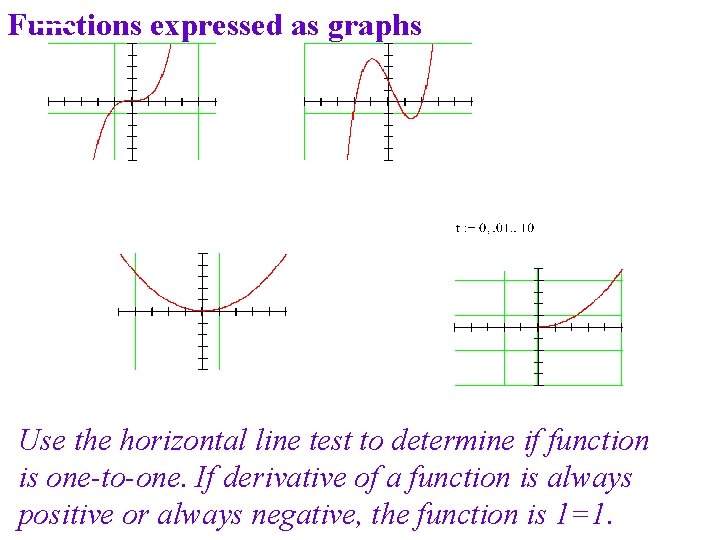
Functions expressed as graphs Use the horizontal line test to determine if function is one-to-one. If derivative of a function is always positive or always negative, the function is 1=1.

Restricting Domains Not 1 -1 Restrict domain to x 0 Now function is 1 -1 and has an inverse function You can make a function 1 -1 by restricting its domain. Such a function will have an inverse.

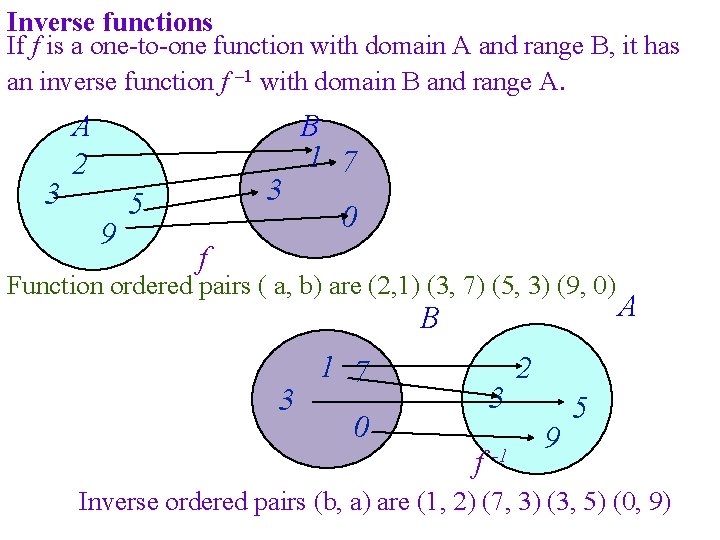
Inverse functions If f is a one-to-one function with domain A and range B, it has an inverse function f – 1 with domain B and range A. 3 A 2 9 3 5 B 1 7 0 f Function ordered pairs ( a, b) are (2, 1) (3, 7) (5, 3) (9, 0) B 3 1 7 0 3 f -1 A 2 9 5 Inverse ordered pairs (b, a) are (1, 2) (7, 3) (3, 5) (0, 9)

How to find the inverse of a one-to-one-function 1. 2. 3. 4. Replace f(x) with y Interchange x and y Solve the equation for x in terms of y (if possible) Replace y with f -1 (x)

f and f – 1 are inverses if and only if the result of the composition of a function and its inverse (in either order is the original input, x. f ={(2, 1) (3, 7) (5, 3) (9, 0)} f – 1(f (2)) = f – 1(1)= 2 f -1 = {(1, 2) (7, 3) (3, 5) (0, 9)} and f (f – 1(1) = f(2) =1 Use the composition of functions to show inverses

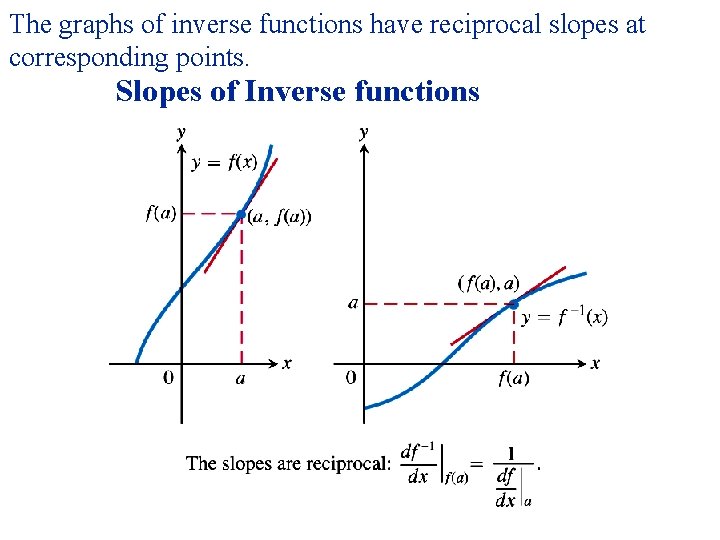
The graphs of inverse functions have reciprocal slopes at corresponding points. Slopes of Inverse functions

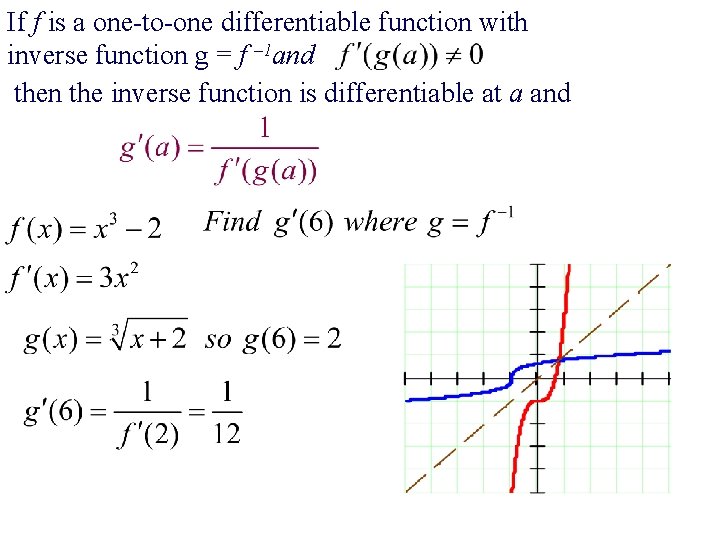
If f is a one-to-one differentiable function with inverse function g = f – 1 and then the inverse function is differentiable at a and

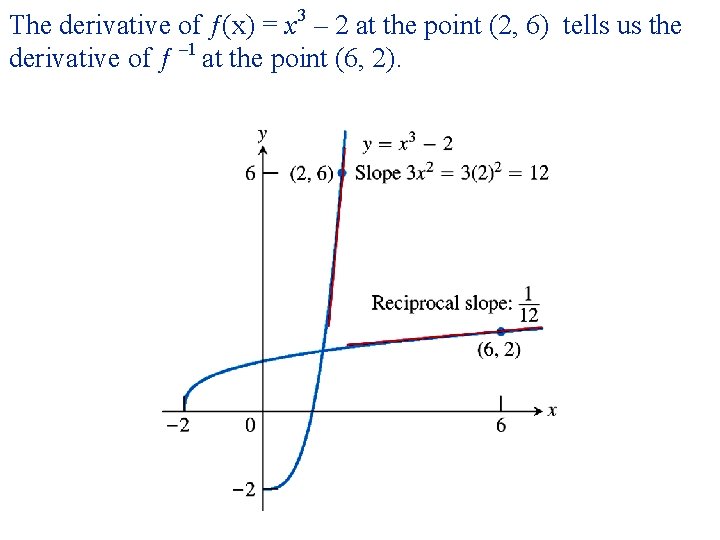
The derivative of ƒ(x) = x 3 – 2 at the point (2, 6) tells us the derivative of ƒ – 1 at the point (6, 2).

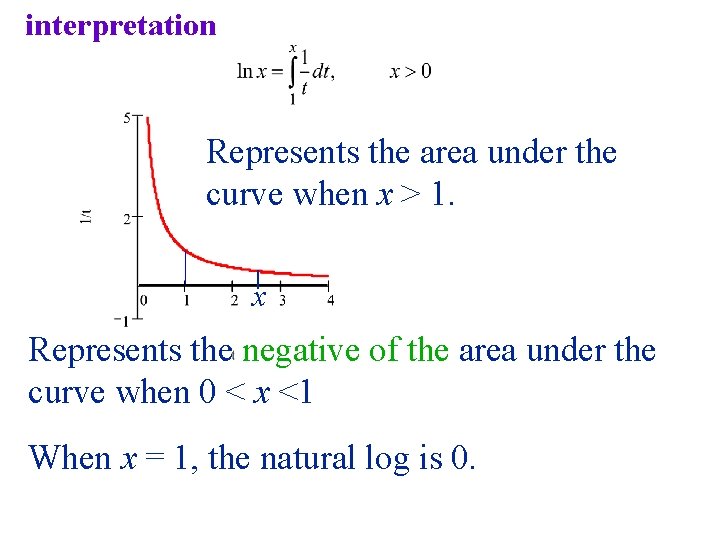
7. 2*New way to define a function From Calculus I: To investigate case for n = -1, we will define the integral as a new function. f(x) is called the natural logarithm f(x) = ln x • Domain is set of all positive real numbers. • Range is all reals • For x > 1, ln x is positive. • For 0 < x < 1, ln x is negative • ln 1 = 0

interpretation Represents the area under the curve when x > 1. x Represents the negative of the area under the curve when 0 < x <1 When x = 1, the natural log is 0.

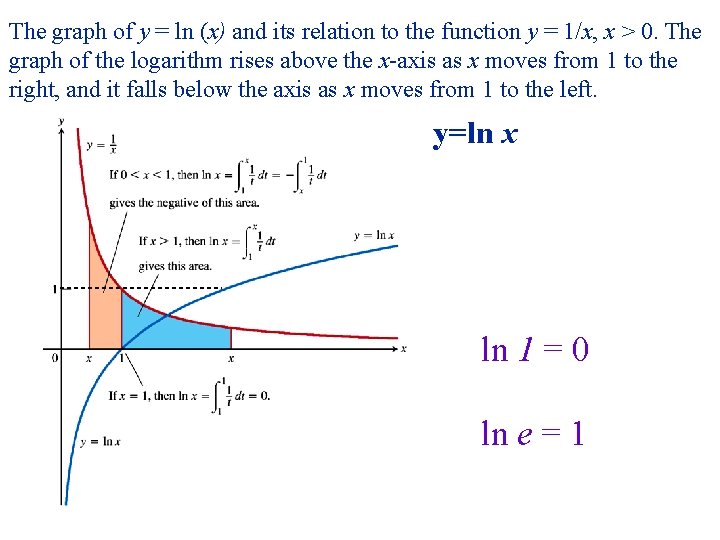
Characteristics of graph of y = ln x is an antiderivative of 1/x. Since x is positive, 1/x is also positive so the slope of ln x is always positive and ln x is increasing. The second derivative of ln x is The second derivative is always negative. ln x is always concave down. So, ln x is increasing, concave down and goes through (1, 0)

The graph of y = ln (x) and its relation to the function y = 1/x, x > 0. The graph of the logarithm rises above the x-axis as x moves from 1 to the right, and it falls below the axis as x moves from 1 to the left. y=ln x ln 1 = 0 ln e = 1

Differentiation of Natural Log Functions Examples (a)

Differentiation of Natural Log Functions Answers 1) Chain rule (a) 1) Chain rule 1) Product rule 1) power rule

Properties of natural logs • ln(1) = 0 • ln(ax) = ln(a) + ln (x) • ln(xn) = n ln x • ln(a/x) = ln (a) – ln (x) Expand Logarithmic expressions to sums (a) (b) ln (x 2 – 3)5 (c)

Expanding Logarithmic expressions to sums (a) = ln (3 x +1) – ln (5 x-2) (b) ln (x 2 – 3)5 = 5 ln (x 2 – 3) (c)

Logarithmic differentiation • Use properties of logs to expand then find the derivative (a) y = (3 x + 1)(5 x - 2)(7 x 2 +4) (b)

• y = (3 x + 1)(5 x - 2)(7 x 2 +4) • Take natural log of each side • ln y = ln ( 1) (3 x. + 1)(5 x - 2)(7 x 2 +4)) • Use the properties of logs to rewrite • ln y = ln (3 x + 1)+ ln(5 x - 2)+ ln(7 x 2 +4) • Differentiate both sides Solve for y’ Replace y with function of x.

• Take natural log of each side • Use the properties of logs to rewrite • Differentiate both sides Solve for y’ Replace y with function of x.

Integration involving the natural log function Examples

Solutions u=x 2 - 3 du=2 xdx u=3 + cos x du=-sin x dx u=cos x du=-sin x dx

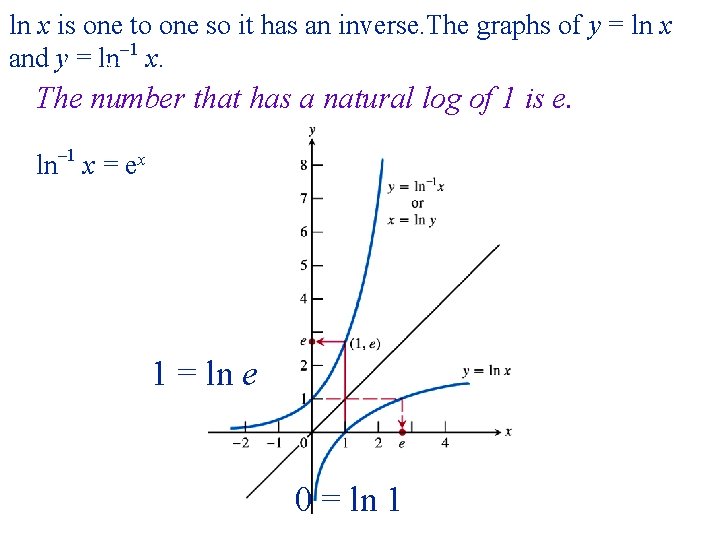
ln x is one to one so it has an inverse. The graphs of y = ln x and y = ln– 1 x. 7. 3*Inverse of ln The number that has a natural log of 1 is e. ln– 1 x = ex 1 = ln e 0 = ln 1

Cancellation properties Since ex and ln x are inverse functions ln ex = x lne = x elnx = x ln e 5 = 5 lne = 5 eln 7 = 7
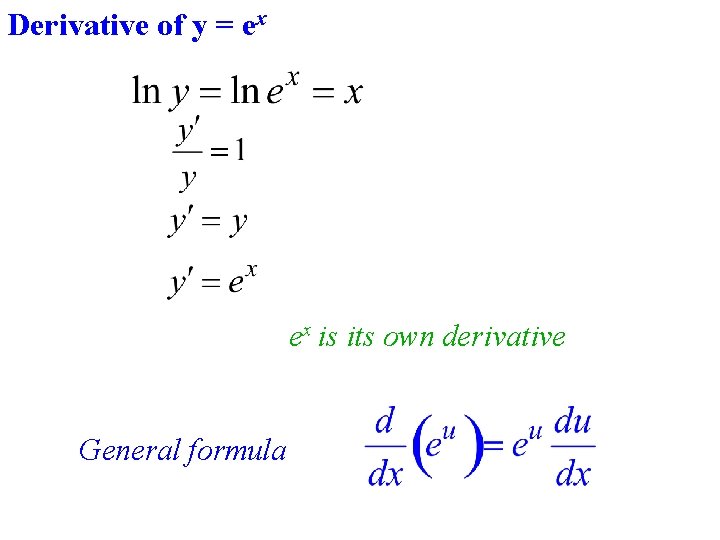
Derivative of y = ex ex is its own derivative General formula
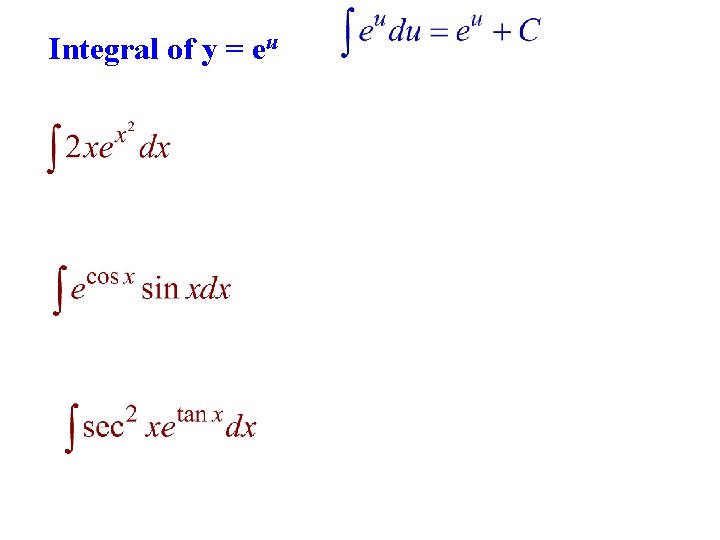
Integral of y = eu

Integral of y = eu 1. u=x 2 du=2 x dx 2. u=cos x du=-sin x dx 3. u=tan x du = sec 2 x dx

7. 4 Logs with other bases 1) 2) Hint: ln a is a constant factor

Logs with other bases u=ln 7 x du = 1/x dx

Exponential functions decrease if 0 < a < 1 and increase if a > 1. As x , we have ax 0 if 0 < a < 1 and ax if a > 1. As x – , we have ax if 0 < a < 1 and ax 0 if a > 1. Exponential functions

7. 4 Exponential functions with other bases General formula (using the chain rule):

Exponential functions with other bases General formula where u = f(x)

Exponential functions with other bases

Review questions Find the derivative for:

Answers to Review questions

Answers to review questions

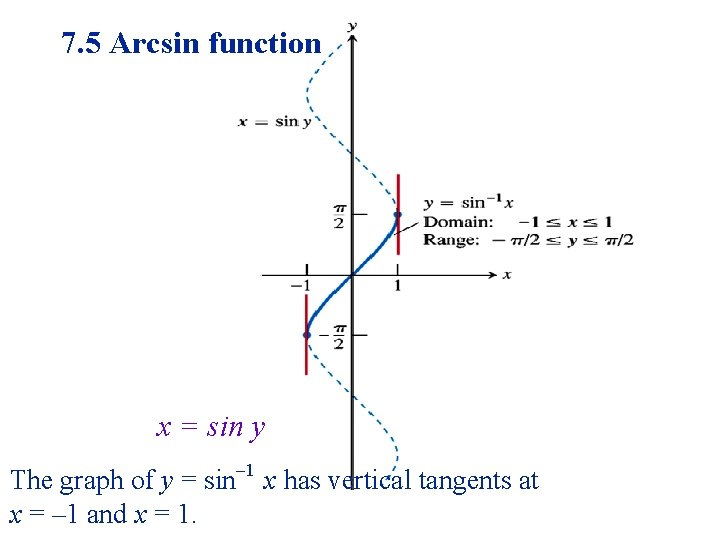
7. 5 Arcsin function x = sin y The graph of y = sin– 1 x has vertical tangents at x = – 1 and x = 1.

Derivative of inverse sine y = sin-1 x is equivalent to sin y = x Using implicit differentiation, cos y y = 1 1 y) x If y = sin-1 u Find the derivative for y = tan-1 u and sec-1 u.

Using inverse cofunction identities, find the derivatives of the inverse cofunctions. The derivative of the inverse cofunction is the negative of the derivative of the function.

Derivatives of inverse trig functions

Integrals

Integrals

Answers Pattern recognition Is the key to solving These.


Complete the Trigonometric Integrals

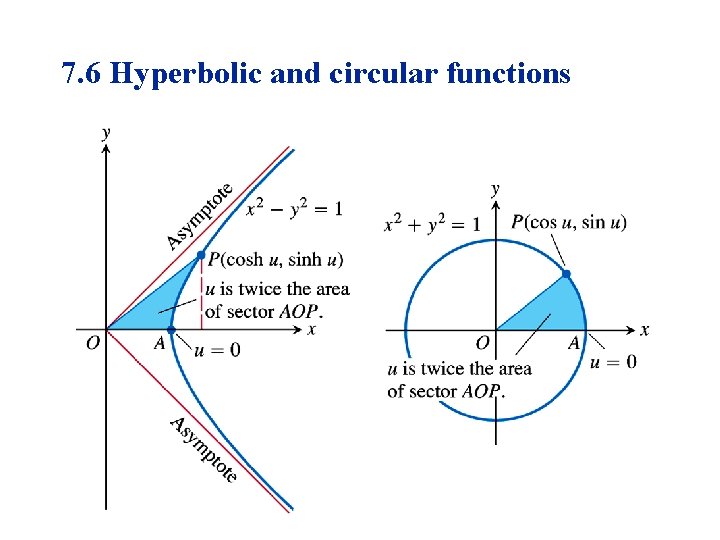
7. 6 Hyperbolic and circular functions

Definitions of Hyperbolic functions

Derivatives of Hyperbolic functions

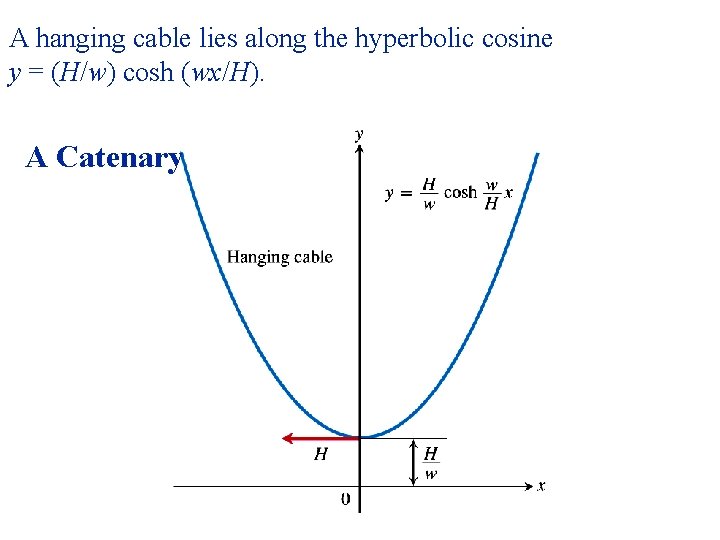
A hanging cable lies along the hyperbolic cosine y = (H/w) cosh (wx/H). A Catenary

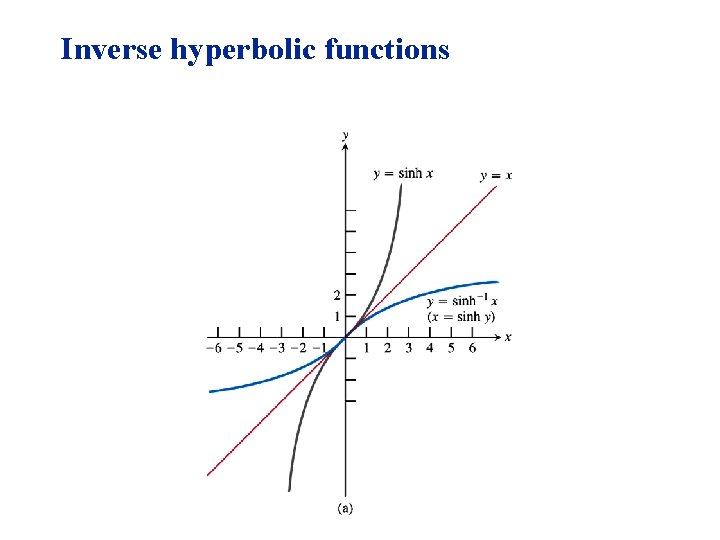
Inverse hyperbolic functions

Derivatives of inverse hyperbolic functions

Integrals leading to inverse hyperbolic functions. Interesting but you will learn how to do these in an easier way next chapter. They won’t be on your test!! Another example of integrals of algebraic functions Leading to transcendentals.

Inverse Hyperbolics as Natural Log functions Skip this for now.

Inverse Hyperbolics as Natural Log functions skip this-not on test.

Indeterminate forms. Determinate forms 0 0 0 - 1

L’Hôpital’s Rule Let f and g be functions that are differentiable on an interval (a, b) containing c except possible at c itself. Assume that g (x) 0. If produces the indeterminate form, then This result applies to the following indeterminate forms:

0 0 Since the indeterminate form results, apply L’Hôpital’s Rule.

Since the indeterminate form results, apply L’Hôpital’s Rule.

Since the indeterminate form results, apply L’Hôpital’s Rule. - - Since the indeterminate form results, apply L’Hôpital’s Rule again.

Indeterminate form 0* rewrite Since the indeterminate form results, apply L’Hôpital’s Rule.

Indeterminate forms involving variable bases and variable exponents leading to

Indeterminate forms involving 0 0
 Lesson 6-2 graphs of inverse functions
Lesson 6-2 graphs of inverse functions Determinant multiplication
Determinant multiplication Inverse functions notes
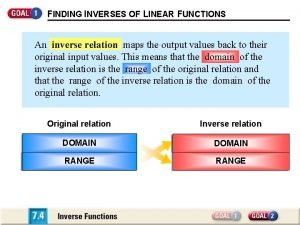
Inverse functions notes 4-2 inverses of relations and functions
4-2 inverses of relations and functions Functions and inverses
Functions and inverses 4-2 practice b inverses of relations and functions
4-2 practice b inverses of relations and functions 6-3 solving linear systems using inverses and cramer's rule
6-3 solving linear systems using inverses and cramer's rule Inequalities inverses and contrapositives
Inequalities inverses and contrapositives How to find inverse of logarithmic function
How to find inverse of logarithmic function Point indifférent diagramme binaire
Point indifférent diagramme binaire Diagrammes binaires
Diagrammes binaires Ses versailles cours inversés
Ses versailles cours inversés 4-7 practice inverse linear functions
4-7 practice inverse linear functions 13-4 inverses of trigonometric functions answers
13-4 inverses of trigonometric functions answers Inverses of linear functions
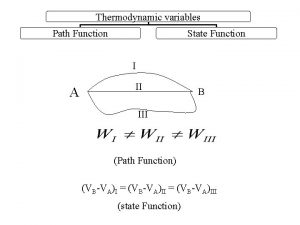
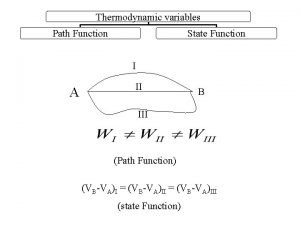
Inverses of linear functions Heat capacity is state or path function
Heat capacity is state or path function Function or not a function
Function or not a function What is function prototype
What is function prototype Why do we study thermodynamics
Why do we study thermodynamics Rational functions parent function
Rational functions parent function Transformations of a rational function
Transformations of a rational function Pressure is state function or path function
Pressure is state function or path function Log parent function
Log parent function How to identify linear functions from tables
How to identify linear functions from tables Exponential parent function
Exponential parent function Pressure is state function or path function
Pressure is state function or path function 1-6 relations and functions answers
1-6 relations and functions answers Parent functions notes
Parent functions notes Piecewise function absolute value
Piecewise function absolute value Direct substitution polynomial
Direct substitution polynomial A rational function of the form
A rational function of the form How a predicate function become a propositional function?
How a predicate function become a propositional function? Linear quadratic cubic reciprocal
Linear quadratic cubic reciprocal Reverse exponential graph
Reverse exponential graph Revenue function from demand function
Revenue function from demand function Polynomial function parent function
Polynomial function parent function Graphing polynomial functions
Graphing polynomial functions Functions of community
Functions of community Content words and function words
Content words and function words Vector function and space curves
Vector function and space curves Difference between procedure and function in sql
Difference between procedure and function in sql Brain structure and function
Brain structure and function Functions of reproductive system
Functions of reproductive system Papez circuit ppt
Papez circuit ppt Circuit diagram of suction machine
Circuit diagram of suction machine Difference between procedure and function in sql
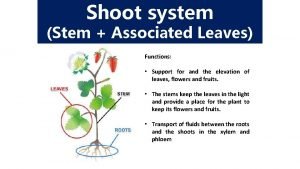
Difference between procedure and function in sql Function of shoot system
Function of shoot system Stress sentence
Stress sentence Positioning and staffing the security function
Positioning and staffing the security function Relation and function
Relation and function Domain and range of an inverse function
Domain and range of an inverse function Domain and range of a rational function
Domain and range of a rational function Function equation
Function equation Personal function of art
Personal function of art Function of pili and fimbriae
Function of pili and fimbriae Poles and zeros of transfer function
Poles and zeros of transfer function Explain about the placement of encryption function.
Explain about the placement of encryption function. Parts of a flower objectives
Parts of a flower objectives The function of the seed
The function of the seed What are the 4 parts of a plant
What are the 4 parts of a plant What is the illuminating parts of microscope
What is the illuminating parts of microscope How to find the x intercept
How to find the x intercept Answer
Answer Calquing elt
Calquing elt