CHAPTER 5 Exponential and Logarithmic Functions 5 1

5. 6 Applications and Models: Growth and Decay; and Compound Interest · · Solve

Population Growth The function P(t) = P 0 ekt, k > 0 can model

Population Growth - Graph Copyright © 2012 Pearson Education, Inc. Publishing as Addison Wesley

Example In 2009, the population of Mexico was about 111. 2 million, and the

Example (continued) Solution: a) At t = 0 (2009), the population was about 111.

Example (continued) c) We are looking for the doubling time; T such that P(T)

Interest Compound Continuously The function P(t) = P 0 ekt can be used to

Example Suppose that $2000 is invested at interest rate k, compounded continuously, and grows

Example (continued) Solution: a. At t = 0, P(0) = P 0 = $2000.

Example (continued) Solution: b. The exponential growth function is P(t) = 2000 e 0.

Example (continued) d. To find the doubling time T, we set P(T) = 2

Growth Rate and Doubling Time The growth rate k and doubling time T are

Example The population of Kenya is now doubling every 25. 8 years. What is

Models of Limited Growth In previous examples, we have modeled population growth. However, in

Models of Limited Growth - Graph Copyright © 2012 Pearson Education, Inc. Publishing as

Exponential Decay, or decline, of a population is represented by the function P(t) =

Graphs Copyright © 2012 Pearson Education, Inc. Publishing as Addison Wesley Slide 5. 6

Decay Rate and Half-Life The decay rate k and the half-life T are related

Example Carbon Dating. The radioactive element carbon-14 has a half-life of 5750 years. The

Example (continued) Solution: First find k when the half-life T is 5750 yr: Now

Example (continued) If the linen wrapping lost 22. 3% of its carbon-14 from the

Slides: 23

Download presentation

CHAPTER 5: Exponential and Logarithmic Functions 5. 1 5. 2 5. 3 5. 4 5. 5 Inverse Functions Exponential Functions and Graphs Logarithmic Functions and Graphs Properties of Logarithmic Functions Solving Exponential and Logarithmic Equations 5. 6 Applications and Models: Growth and Decay; and Compound Interest Copyright © 2012 Pearson Education, Inc. Publishing as Addison Wesley

5. 6 Applications and Models: Growth and Decay; and Compound Interest · · Solve applied problems involving exponential growth and decay. Solve applied problems involving compound interest. Copyright © 2012 Pearson Education, Inc. Publishing as Addison Wesley

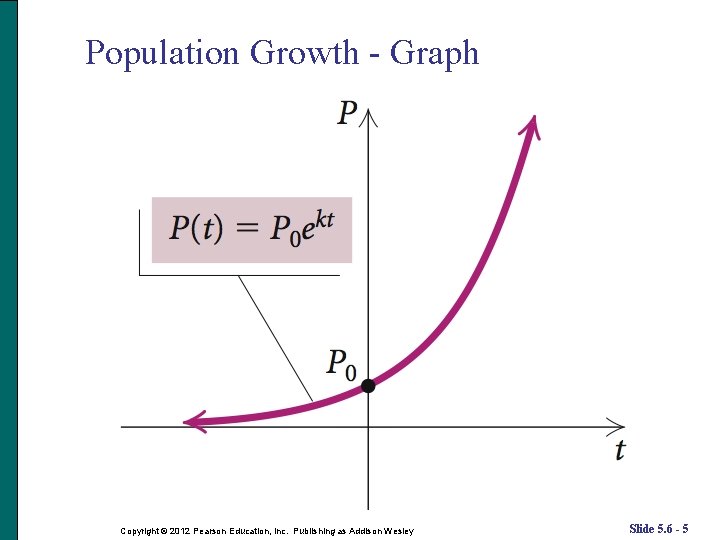
Population Growth The function P(t) = P 0 ekt, k > 0 can model many kinds of population growths. In this function: P 0 = population at time 0, P(t) = population after time t, t = amount of time, k = exponential growth rate. The growth rate unit must be the same as the time unit. Copyright © 2012 Pearson Education, Inc. Publishing as Addison Wesley Slide 5. 6 - 4

Example In 2009, the population of Mexico was about 111. 2 million, and the exponential growth rate was 1. 13% per year. a) Find the exponential growth function. b) Estimate the population in 2014. c) After how long will the population be double what it was in 2009? Copyright © 2012 Pearson Education, Inc. Publishing as Addison Wesley Slide 5. 6 - 6

Example (continued) Solution: a) At t = 0 (2009), the population was about 111. 2 million. We substitute 111. 2 for P 0 and 1. 13% or 0. 0113 for k to obtain the exponential growth function. P(t) = 111. 2 e 0. 113 t b) In 2014, t = 5; that is 5 years have passed since 2009. To find the population in 2014, we substitute 5 for t. The population will be about 117. 7 million in 2014. Copyright © 2012 Pearson Education, Inc. Publishing as Addison Wesley Slide 5. 6 - 7

Example (continued) c) We are looking for the doubling time; T such that P(T) = 2 • 111. 2 or 222. 4. Solve The population of Mexico will be double what it was in 2009 about 61. 3 years after 2009. Copyright © 2012 Pearson Education, Inc. Publishing as Addison Wesley Slide 5. 6 - 8

Interest Compound Continuously The function P(t) = P 0 ekt can be used to calculate interest that is compounded continuously. In this function: P 0 = amount of money invested, P(t) = balance of the account after t years, t = years, k = interest rate compounded continuously. Copyright © 2012 Pearson Education, Inc. Publishing as Addison Wesley Slide 5. 6 - 9

Example Suppose that $2000 is invested at interest rate k, compounded continuously, and grows to $2504. 65 after 5 years. a. b. c. d. What is the interest rate? Find the exponential growth function. What will the balance be after 10 years? After how long will the $2000 have doubled? Copyright © 2012 Pearson Education, Inc. Publishing as Addison Wesley Slide 5. 6 - 10

Example (continued) Solution: a. At t = 0, P(0) = P 0 = $2000. Thus the exponential growth function is P(t) = 2000 ekt. We know that P(5) = $2504. 65. Substitute and solve for k: The interest rate is about 0. 045 or 4. 5%. Copyright © 2012 Pearson Education, Inc. Publishing as Addison Wesley Slide 5. 6 - 11

Example (continued) Solution: b. The exponential growth function is P(t) = 2000 e 0. 045 t. c. The balance after 10 years is Copyright © 2012 Pearson Education, Inc. Publishing as Addison Wesley Slide 5. 6 - 12

Example (continued) d. To find the doubling time T, we set P(T) = 2 • P 0= 2 • $2000 = $4000 and solve for T. Thus the orginal investment of $2000 will double in about 15. 4 yr. Copyright © 2012 Pearson Education, Inc. Publishing as Addison Wesley Slide 5. 6 - 13

Growth Rate and Doubling Time The growth rate k and doubling time T are related by k. T = ln 2 or or Note that the relationship between k and T does not depend on P 0. Copyright © 2012 Pearson Education, Inc. Publishing as Addison Wesley Slide 5. 6 - 14

Example The population of Kenya is now doubling every 25. 8 years. What is the exponential growth rate? Solution: The growth rate of the population of Kenya is about 2. 69% per year. Copyright © 2012 Pearson Education, Inc. Publishing as Addison Wesley Slide 5. 6 - 15

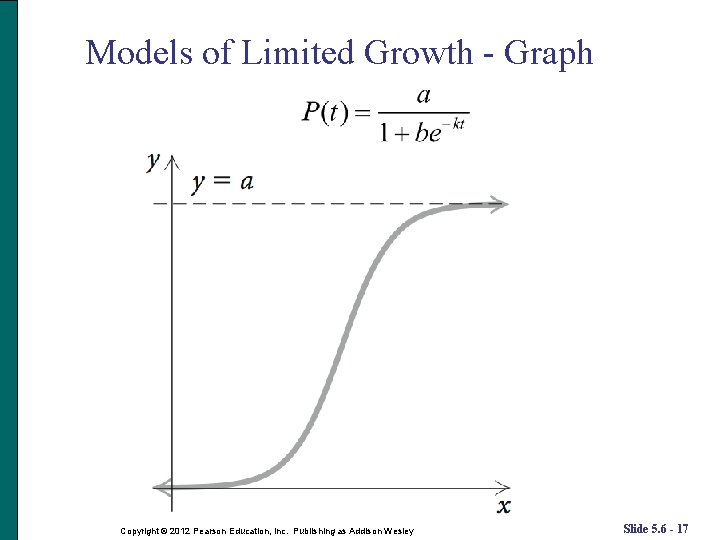
Models of Limited Growth In previous examples, we have modeled population growth. However, in some populations, there can be factors that prevent a population from exceeding some limiting value. One model of such growth is which is called a logistic function. This function increases toward a limiting value a as t approaches infinity. Thus, y = a is the horizontal asymptote of the graph. Copyright © 2012 Pearson Education, Inc. Publishing as Addison Wesley Slide 5. 6 - 16

Exponential Decay, or decline, of a population is represented by the function P(t) = P 0 e kt, k > 0. In this function: P 0 = initial amount of the substance (at time t = 0), P(t) = amount of the substance left after time, t = time, k = decay rate. The half-life is the amount of time it takes for a substance to decay to half of the original amount. Copyright © 2012 Pearson Education, Inc. Publishing as Addison Wesley Slide 5. 6 - 18

Decay Rate and Half-Life The decay rate k and the half-life T are related by k. T = ln 2 or or Note that the relationship between decay rate and halflife is the same as that between growth rate and doubling time. Copyright © 2012 Pearson Education, Inc. Publishing as Addison Wesley Slide 5. 6 - 20

Example Carbon Dating. The radioactive element carbon-14 has a half-life of 5750 years. The percentage of carbon-14 present in the remains of organic matter can be used to determine the age of that organic matter. Archaeologists discovered that the linen wrapping from one of the Dead Sea Scrolls had lost 22. 3% of its carbon-14 at the time it was found. How old was the linen wrapping? Copyright © 2012 Pearson Education, Inc. Publishing as Addison Wesley Slide 5. 6 - 21

Example (continued) If the linen wrapping lost 22. 3% of its carbon-14 from the initial amount P 0, then 77. 7% is the amount present. To find the age t of the wrapping, solve for t: The linen wrapping on the Dead Sea Scrolls was about 2103 years old when it was found. Copyright © 2012 Pearson Education, Inc. Publishing as Addison Wesley Slide 5. 6 - 23