Exponential and Logarithmic Functions 1 2 1 Exponential









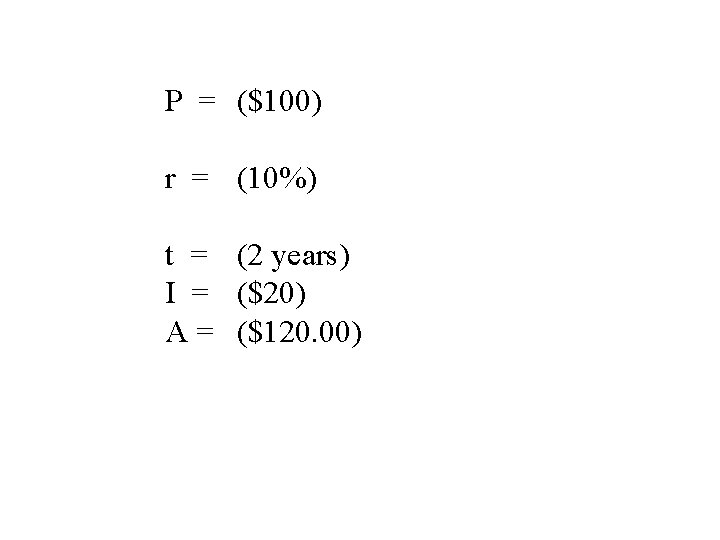












- Slides: 30

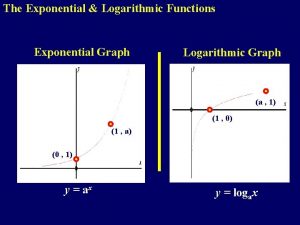
Exponential and Logarithmic Functions 1

2 -1 Exponential Functions Function type linear quadratic polynomial exponential Example f(x) = 3 x + 2 f(x) = 3 x 2 + 2 x - 3 f(x) = 2 x 4 + 3 x 2 f(x) = 2 x f(x) = 2. 63 x-1 2

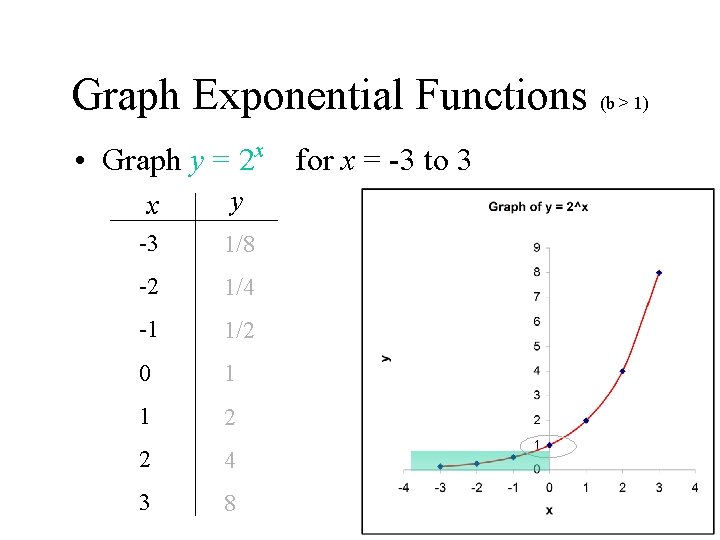
Graph Exponential Functions (b > 1) • Graph y = 2 x for x = -3 to 3 x y -3 1/8 -2 1/4 -1 1/2 0 1 1 2 2 4 3 8

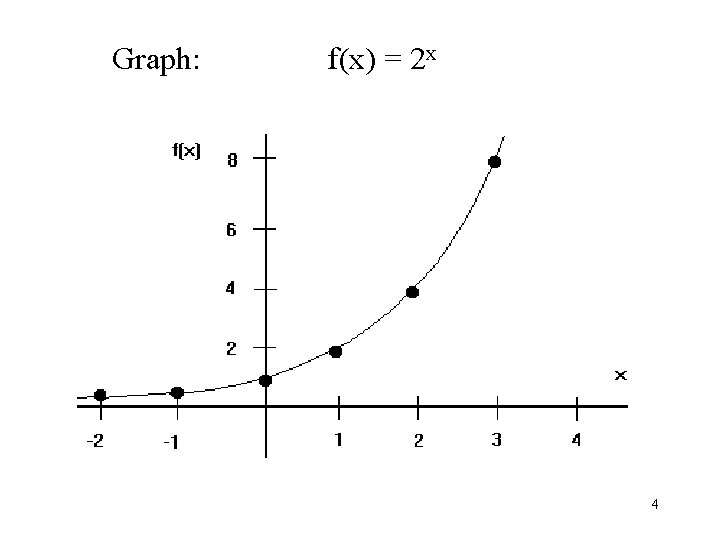
Graph: f(x) = 2 x 4

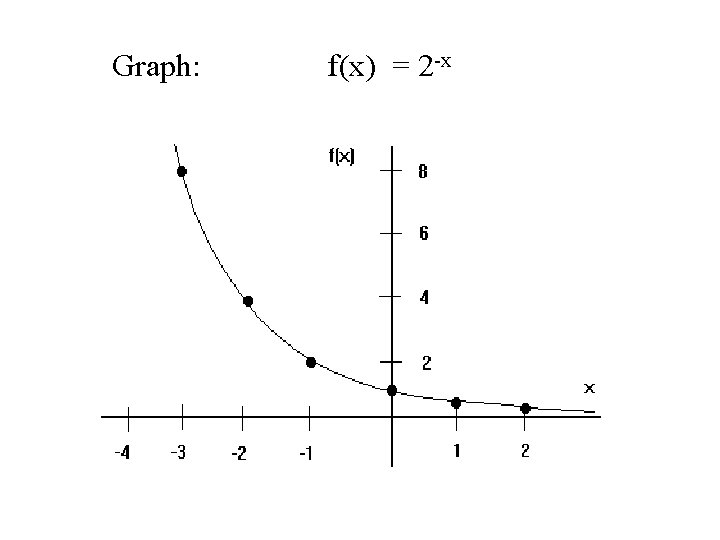
Graph: f(x) = 2 -x

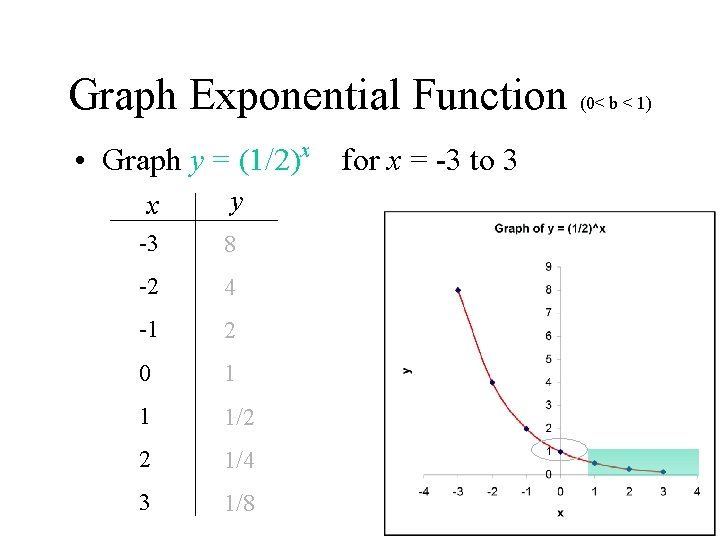
Graph Exponential Function (0< b < 1) • Graph y = (1/2)x for x = -3 to 3 x y -3 8 -2 4 -1 2 0 1 1 1/2 2 1/4 3 1/8

• 2 is the base of the exponential –“exponential base 2” • the base can be any positive number • common bases are 2, 10, and e Exponential functions with base e f(x) = ex • e is a real number constant (like ) value = 2. 7182818… • frequently seen as the base for exponential functions • called the natural base 7

Properties of the exponential functions: • f(x) = bx and f(x) = b-x, - < x < • b is called the base • can always make b > 1 • e. g. f(x) = = 2 -x • domain: (- , ) range: (0, ) • continuous • f(x) = bx is an increasing function • f(x) = b-x is a decreasing function

• y-intercept: y = 1 • no x-intercepts; graph always above x axis • x-axis is an asymptote: as x + for f(x) = b-x as x - for f(x) = bx • bx = by x = y (one-to-one property)

Growth Decay

Exponential function – A function of the form y=abx, where b>0 and b 1. Step 1 – Make a table of values for the function.

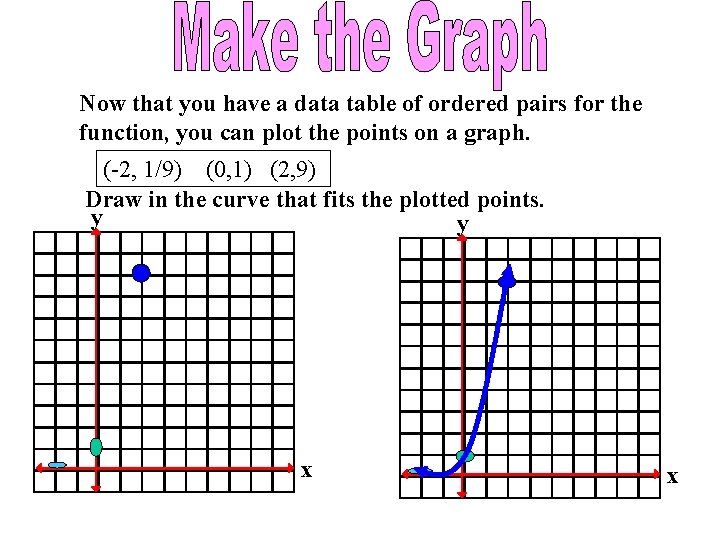
Now that you have a data table of ordered pairs for the function, you can plot the points on a graph. (-2, 1/9) (0, 1) (2, 9) Draw in the curve that fits the plotted points. y y x x

APPLICATION Simple Interest formulas I = Prt A = P + Prt = P(1 + rt)

P = principal invested (also called present value) r = annual interest rate (expressed as a decimal) t = time in years I = interest earned A = total amount after t years (also called future value)

Simple Interest You invest $100. 00 for at 10% simple interest. How much do you have at the end of 2 years? We can do this in our heads: 10% of $100 is $10 that's $10 interest earned per year for 2 years for a total of $20 interest plus the $100 original investment. . . for a new amount of : $120
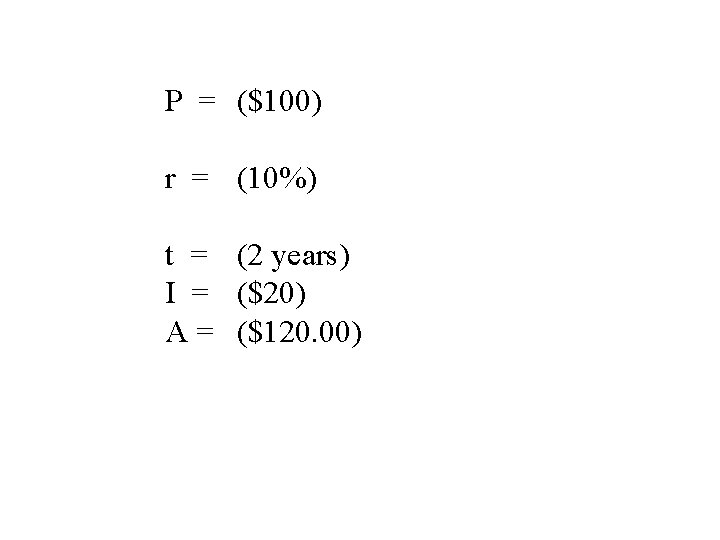
P = ($100) r = (10%) t = (2 years) I = ($20) A = ($120. 00)

If you know any 3 of the variables, the formula (plus some algebra) can be used to solve for the 4 th variable: Example: $100 is invested (simple interest) for 10 years, and the investment doubled in value. What was the interest rate? The equation: 200 = 100(1 + r(10)) Solve: r = 0. 10= (10%)

You deposit $1500 in an account that pays 2. 3% interest compounded yearly, 1) What was the initial principal (P) invested? 2) What is the growth rate (r)? The growth factor? 3) Using the equation A = P(1+r)t, how much money would you have after 2 years if you didn’t deposit any more money? 1) The initial principal (P) is $1500. 2) The growth rate (r) is 0. 023. The growth factor is 1. 023.

2 -2 Logarithmic Functions The common log of a number is that exponent (or power) to which 10 must be raised to obtain the number. Notation: y = log (x) or y = log x "y = log of x" Example: • log (1000) =. . . • . . . the power to which 10 must be raised to obtain 1000 • so log(1000) = 3 19

Another way to put it: 3 = log(1000) because 103 = 1000 y = log(x) means 10 y = x Be CAREFUL! log x + 2 log(x + 2) = log(x) + 2 20

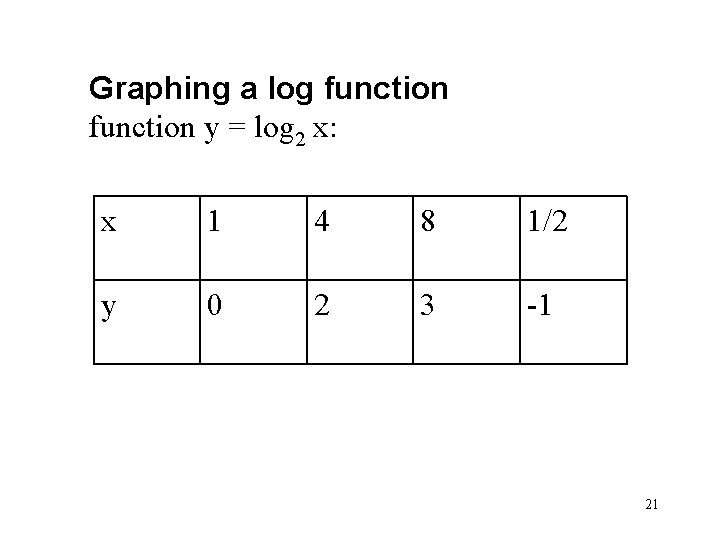
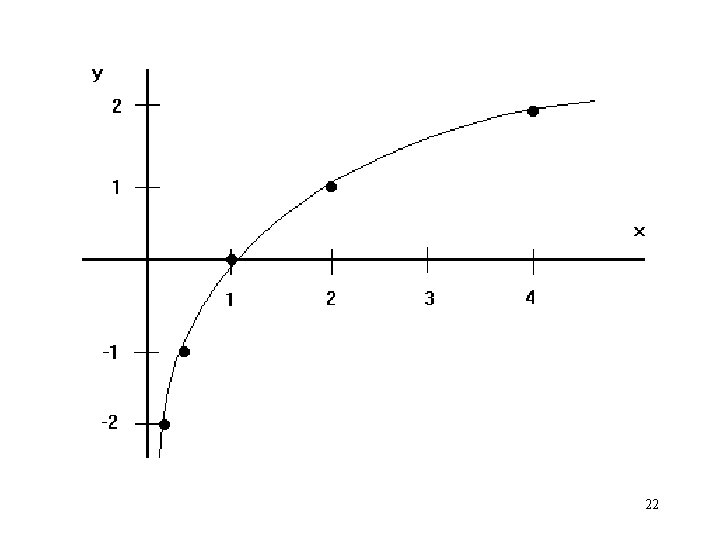
Graphing a log function y = log 2 x: x 1 4 8 1/2 y 0 2 3 -1 21

22

+ Properties of logs Property 1 Recall: if m = 102 then 2 = log m 100000 = 100 x 1000 mn = m x n 105 = 102 x 103 10 log mn = 10 log m x 10 log n 10=mlog mn 10 log exponents) +log mn m = log then x = y) the log of a product = the sum of the logs 23

- Property 2 ================ 100000 1000 m/n = m n 102 = 105 103 10 log m/n = 10 log m 10 log n m m/n 10 log 10=log exponents) - log m/n m = log then x = y) the log of a quotient = the difference of the logs =====================24

Property 3 log mr = log mm … m (for r factors) = log m +. . . + log m (for r terms) = r log mr = r log m the log of a power = the exponent times the log of the base 25

These relationships hold for any base: 1. loga mn = loga m + loga n (log of a product) 2. loga m/n = loga m - loga n (log of a quotient) 3. loga mr = r loga m (log of a power) Each property can be used in two directions, e. g. log (10)(20) = log 10 + log 20 uses property 1 going from left-hand to right-hand side called expansion ( ) 26

log 10 - log 20 = log (10/20) uses property 2 going from right-hand to lefthand side called collection, or writing as the log of a single expression “log expression” ( ) the book directions are “write as a one logarithm” - this is ambiguous. Read “Write as the log of a single expression” 3 log x not acceptable as an answer, but log x 3 27

Examples: Write the equivalent exponential equation and solve for y. Logarithmic Equation y = log 216 y = log 2( ) Equivalent Exponential Equation Solution 16 = 2 y 16 = 24 y = 4 = 2 y = 2 -1 y = – 1 y = log 416 16 = 4 y 16 = 42 y = 2 y = log 51 1=5 y 1 = 50 y = 0 28

Properties of Logarithms 1. loga 1 = 0 since a 0 = 1. 2. loga a = 1 since a 1 = a. 3. loga ax = x and alogax = x inverse property 4. If loga x = loga y, then x = y. one-to-one property Examples: Solve for x: log 6 6 = x log 6 6 = 1 property 2 x = 1 Simplify: log 3 35 = 5 property 3 Simplify: 7 log 79 = 9 property 3 29

Properties of Natural Logarithms 1. ln 1 = 0 since e 0 = 1. 2. ln e = 1 since e 1 = e. 3. ln ex = x and eln x = x inverse property 4. If ln x = ln y, then x = y. one-to-one property Examples: Simplify each expression. inverse property 2 property 1 30
 Unit 8 exponential and logarithmic functions
Unit 8 exponential and logarithmic functions Unit 5: exponential and logarithmic functions answers
Unit 5: exponential and logarithmic functions answers Y=ab^x
Y=ab^x Chapter 6 exponential and logarithmic functions answers
Chapter 6 exponential and logarithmic functions answers Chapter 4 exponential and logarithmic functions
Chapter 4 exponential and logarithmic functions Solving exponential and logarithmic equations worksheet
Solving exponential and logarithmic equations worksheet Lesson 10-2 exponential growth and decay
Lesson 10-2 exponential growth and decay Property of equality for exponential functions
Property of equality for exponential functions Transforming exponential and logarithmic functions
Transforming exponential and logarithmic functions Reverse exponential graph
Reverse exponential graph Lesson 5-2
Lesson 5-2 Expanding natural logarithms
Expanding natural logarithms Chapter 9 exponential and logarithmic functions answer key
Chapter 9 exponential and logarithmic functions answer key Chapter 9 exponential and logarithmic functions answer key
Chapter 9 exponential and logarithmic functions answer key Chapter 5 exponential and logarithmic functions answer key
Chapter 5 exponential and logarithmic functions answer key Transcendental functions examples with solutions
Transcendental functions examples with solutions Solving exponential calculator
Solving exponential calculator Inverse function graph examples
Inverse function graph examples Integration of exponent
Integration of exponent Chapter 5 exponential and logarithmic functions
Chapter 5 exponential and logarithmic functions Chapter 3 exponential and logarithmic functions
Chapter 3 exponential and logarithmic functions 7-5 exponential and logarithmic equations and inequalities
7-5 exponential and logarithmic equations and inequalities Exponential and logarithmic equations and inequalities
Exponential and logarithmic equations and inequalities Logarithmic inequality example
Logarithmic inequality example Exponential equations examples
Exponential equations examples Exponential and logarithmic equations and inequalities
Exponential and logarithmic equations and inequalities Modeling with exponential and logarithmic equations quiz
Modeling with exponential and logarithmic equations quiz Log form to exponential form
Log form to exponential form 3-4 exponential and logarithmic equations
3-4 exponential and logarithmic equations 3-4 exponential and logarithmic equations
3-4 exponential and logarithmic equations Logarithm
Logarithm