Chapter 6 Exponential and Logarithmic Functions and Applications

Chapter 6 Exponential and Logarithmic Functions and Applications Section 6. 4

Section 6. 4 Exponential and Logarithmic Equations • Solving Exponential Equations o Exponential Equality Property o Base 10 or Base e o Graphically • Fundamental Properties of Logarithms o Solving Exponential Equations Using Properties of Logarithms • Solving Logarithmic Equations • Solving Literal Equations Involving Exponential and Logarithmic Equations • Change of Base Formula • Applications

Exponential Equality Property: For b > 0 and b 1, if bm = bn, then m = n. *Solving Exponential Equations with the Exponential Equality Property: 1. Express each side of the equation as a power of the same base. 2. Apply the exponential equality property to equate the exponents. 3. Solve for the variable. 4. Check your solution. *Also referred to as solving by "equating the bases" or "relating the bases. "

Use the exponential equality property to solve 2 92 x + 4 = 162. Step 1. Express each side of the equation as a power of the same base. First, we divide both sides of 2 92 x + 4 = 162 by “ 2. ” 92 x + 4 = 81 Next, we express each side of the equation as a power of “ 3. ” (3 2)2 x + 4 = 34 3 4 x + 8 = 34 Make sure to distribute correctly: 2(2 x + 4) = 4 x + 8 Steps 2 -3. Apply the exponential equality property to equate the exponents. Solve for the variable. 4 x + 8 = 4 x = – 1 Step 4. Check your solution. 2 9[2(– 1) + 4] = 162 2 92 = 162 2(81) = 192 True

Use the exponential equality property to solve Check:

Solving Exponential Equations with Base 10 or Base e. 1. Isolate the power (the term containing the variable exponent) on one side of the equation. If necessary, divide both sides of the equation by any coefficient of the power term. 2. Convert the equation to logarithmic form. 3. Solve for the variable. Use a calculator if necessary. 4. Check your solution.

Solve the exponential equation 2(– 6 + 102 x) = 16. 26. your answer to 4 decimal places as needed. Round Step 1. Isolate the power. First, divide both sides of the equation by “ 2. ” Then, add “ 6” to both sides of the equation. – 6 + 102 x = 8. 13 10 2 x = 14. 13 Step 2. Convert the equation to logarithmic form. log 1014. 13 = 2 x or log 14. 13 = 2 x Step 3. Solve for the variable. x = log 14. 13 2 x 0. 5751 Step 4. Check your solution. 2[– 6 + 10(2 0. 5751)] = 16. 26 2(8. 1319) = 16. 2638 16. 26

Solve the exponential equation 25. 6 = – 2 + 3. 1 e– 0. 15 x. Round your answer to 4 decimal places as needed. 27. 6 = 3. 1 e– 0. 15 x 3. 1 8. 9032 = loge 8. 9032 = – 0. 15 x or e– 0. 15 x ln 8. 9032 = – 0. 15 x x = ln 8. 9032 – 0. 15 x – 14. 5761 You can check the answer.

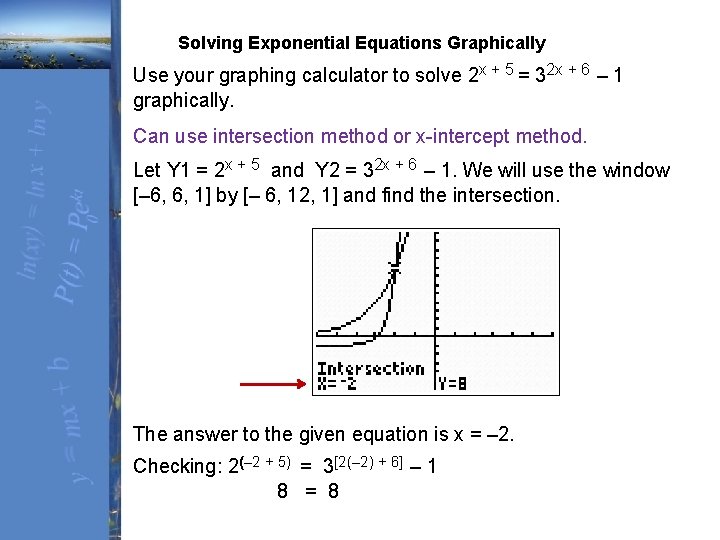
Solving Exponential Equations Graphically Use your graphing calculator to solve 2 x + 5 = 32 x + 6 – 1 graphically. Can use intersection method or x-intercept method. Let Y 1 = 2 x + 5 and Y 2 = 32 x + 6 – 1. We will use the window [– 6, 6, 1] by [– 6, 12, 1] and find the intersection. The answer to the given equation is x = – 2. Checking: 2(– 2 + 5) = 3[2(– 2) + 6] – 1 8 = 8

Recall the Basic Properties of Logarithms: For b > 0 and b 1, logb 1 = 0, logb b = 1, logb bx = x, and Fundamental Properties of Logarithms For positive real numbers M, N, and b, b 1, and any real number k: Product Property: Quotient Property: Power Property: Note: These properties apply to natural logarithms as well.

Use the fact that log 3 4 = 1. 2619 and log 3 7 = 1. 7712 and the properties of logarithms to estimate the value of the following expressions. Round your answers to 4 decimal places as needed. a. log 3 28 = log 3 (4 7) = log 3(4) + log 3(7) = 1. 2619 + 1. 7712 = 3. 0331 b. log 3 (1. 75) = log 3 (7/4) = log 3(7) – log 3(4) = 1. 7712 – 1. 2619 = 0. 5093 c.

Use the properties of logarithms to rewrite each expression as a single logarithm. a. 5 log x + log 9 = log x 5 + log 9 = log (9 x 5) b. log (x + 3) – log (x 2 – 9) c. or

Expand the given expression in terms of simpler logarithms. Assume that all variable expressions are positive real numbers.

Solving Exponential Equations Using Properties of Logarithms 1. Isolate the power on one side of the equation. 2. Take the logarithm of both sides of the equation; may take either the common logarithm (base 10) or a natural logarithm (base e). 3. Apply the power property of logarithms to simplify (that is, "bring down" the variable exponent to the front). 4. Solve for the variable. 5. Check your solution.

Solve the exponential equation – 7 + 4 x = 5. Round your answer to 4 decimal places. Step 1: Isolate the power on one side of the equation. 4 x = 12 Step 2: Take the logarithm of both sides of the equation. log 4 x = log 12 Step 3: Apply the power property of logarithms. x log 4 = log 12 Step 4: Solve for the variable. 5. Check your solution. – 7 + 4(1. 7925) 5

Solve the exponential equation 27 ex – 2 = 7. Round your answer to 4 decimal places. ex – 2 = 0. 2593 ln ex – 2 = ln 0. 2593 (x – 2) ln e = ln 0. 2593 (x – 2) (1) = ln 0. 2593 (Recall ln e is equivalent to loge e) x = ln 0. 2593 + 2 x 0. 6502 Checking: 27 e(0. 6502 – 2) 7

Logarithmic Equality Property: For positive real numbers m, n, and b, b 1, if logb m = logb n, then m = n. Solving Logarithmic Equations: 1. Isolate the logarithmic expression on one side of the equation. If needed, apply the properties of logarithms to combine all logarithms as a single logarithm. 2. Convert the logarithmic equation to an exponential equation. 3. Solve for the variable. 4. Check for possible extraneous solutions.

Solve the logarithmic equation 6 log 4 x = 18. Step 1. Isolate the logarithmic expression on one side of the equation. log 4 x = 3 Step 2: Convert the logarithmic equation to an exponential equation. 103 = 4 x Step 3: Solve for the variable. 4 x = 1000 x = 250 Step 4: Check for possible extraneous solutions. 6 log [4(250)] = 18 18 = 18

Solve the logarithmic equation We discard x = – 10/3 (it is not in the domain). Thus, x = 10. You can verify the solution.

Solve the equation ln x + ln (x + 3) = ln (x + 15). ln [x(x + 3)] = ln (x + 15) ln (x 2 + 3 x) = ln (x + 15) x 2 + 3 x = x + 15 Logarithmic equality x 2 + 3 x – 15 = 0 x 2 + 2 x – 15 = 0 (x + 5)(x – 3) = 0 x = – 5 or x = 3 We discard x = – 5 (it is not in the domain). Thus, x = 3. You can verify the solution.

Solve the equation ln (2 x – 1) = 3 and approximate your answer to 4 decimal places. Recall ln (2 x – 1) = 3 is equivalent to loge(2 x – 1) = 3 e 3 = 2 x – 1 2 x = e 3 + 1 2 x = 21. 085537 x 10. 5428

Solving Literal Equations Involving Exponential or Logarithmic Equations Solve for y:

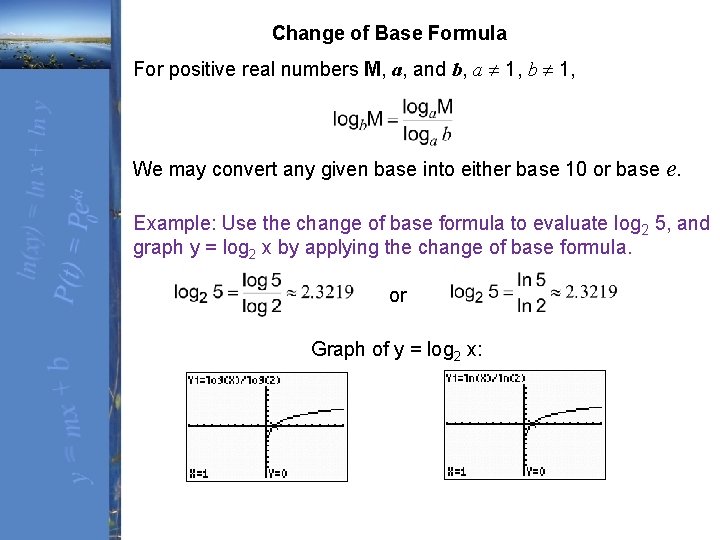
Change of Base Formula For positive real numbers M, a, and b, a 1, b 1, We may convert any given base into either base 10 or base e. Example: Use the change of base formula to evaluate log 2 5, and graph y = log 2 x by applying the change of base formula. or Graph of y = log 2 x:

The function P(t) = 89. 371(3. 2)t models the number of digital 3 D screens worldwide for t number of years after 2005. Using this model, estimate when the number of digital 3 D screens worldwide reached approximately 9, 000. Solve algebraically and round your answer to the nearest whole number. Source: mpaa. org. The number of digital 3 D screens reached approximately 9, 000 in 2009.

The number of prohibited firearms intercepted by the Transportation Security Administration (TSA) at U. S. airport screenings from 2005 to 2009 can be modeled by the function f(x) = 2391. 893 – 931. 691 ln x, where x = 1 represents 2005, x = 2 is 2006, and so on. Use this model to estimate when the TSA intercepted approximately 892 firearms. Round your answer to the nearest whole number. Sources: www. aaa. com; www. safecarguide. com The TSA intercepted approximately 892 firearms in 2009.

Using your textbook, practice the problems assigned by your instructor to review the concepts from Section 6. 4.