Chapter 4 Trigonometric Functions 4 5 MATHPOWERTM 12

Chapter 4 Trigonometric Functions 4. 5 MATHPOWERTM 12, WESTERN EDITION 4. 5. 1

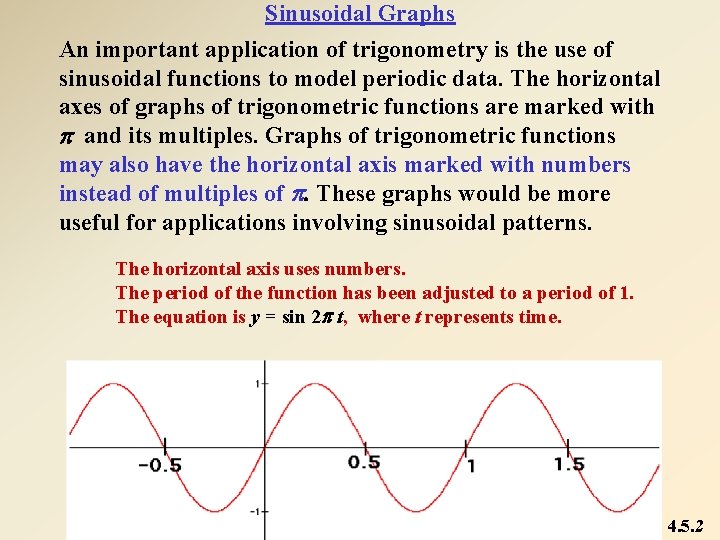
Sinusoidal Graphs An important application of trigonometry is the use of sinusoidal functions to model periodic data. The horizontal axes of graphs of trigonometric functions are marked with p and its multiples. Graphs of trigonometric functions may also have the horizontal axis marked with numbers instead of multiples of p. These graphs would be more useful for applications involving sinusoidal patterns. The horizontal axis uses numbers. The period of the function has been adjusted to a period of 1. The equation is y = sin 2 p t, where t represents time. 4. 5. 2

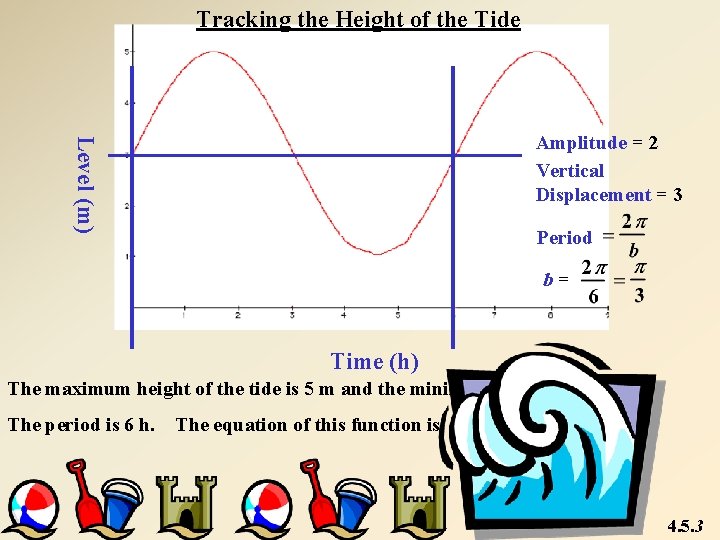
Tracking the Height of the Tide Level (m) Amplitude = 2 Vertical Displacement = 3 Period b= Time (h) The maximum height of the tide is 5 m and the minimum height is 1 m. The period is 6 h. The equation of this function is 4. 5. 3

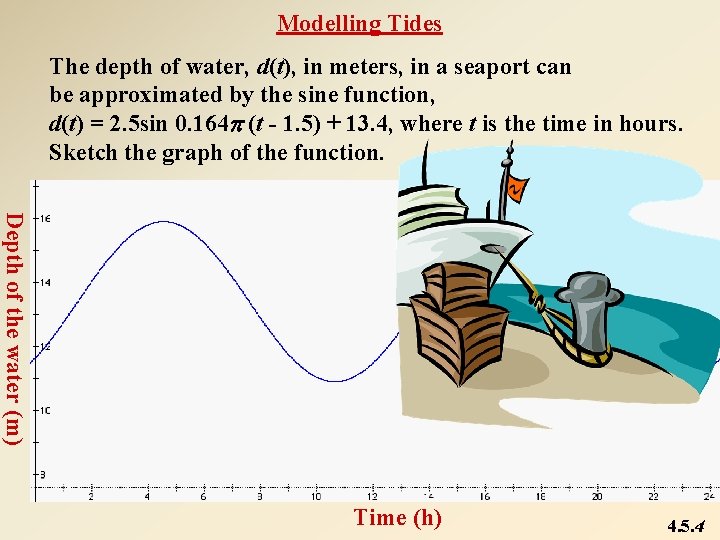
Modelling Tides The depth of water, d(t), in meters, in a seaport can be approximated by the sine function, d(t) = 2. 5 sin 0. 164 p (t - 1. 5) + 13. 4, where t is the time in hours. Sketch the graph of the function. Depth of the water (m) Time (h) 4. 5. 4

Modelling Tides [cont’d] Depth of the water (m) Maximum = 15. 9 12. 2 h 8. 751 0. 346 Minimum = 10. 9 d(t) = 2. 5 sin 0. 164 p (t - 1. 5) + 13. 4 Amplitude = 2. 5 m Period = 12. 2 h Time (h) Phase Shift = 1. 5 units to the right Find the time for which the depth of the water is at least 12 m: 8. 751 - 0. 346 = 8. 4 h for each cycle. 4. 5. 5

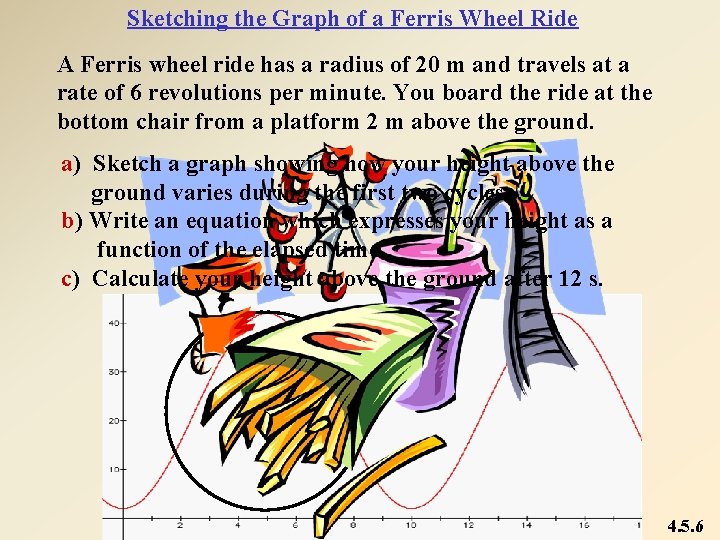
Sketching the Graph of a Ferris Wheel Ride A Ferris wheel ride has a radius of 20 m and travels at a rate of 6 revolutions per minute. You board the ride at the bottom chair from a platform 2 m above the ground. a) Sketch a graph showing how your height above the ground varies during the first two cycles. b) Write an equation which expresses your height as a function of the elapsed time. c) Calculate your height above the ground after 12 s. 4. 5. 6

Height (m) Sketching the Graph of a Ferris Wheel Ride [cont’d] Time (s) The equation is: The height after 12 s is 15. 9 m. or 4. 5. 7

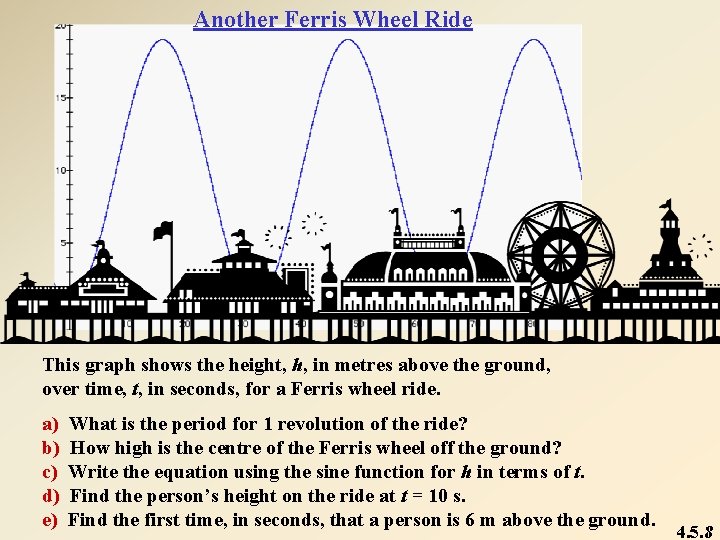
Another Ferris Wheel Ride This graph shows the height, h, in metres above the ground, over time, t, in seconds, for a Ferris wheel ride. a) b) c) d) e) What is the period for 1 revolution of the ride? How high is the centre of the Ferris wheel off the ground? Write the equation using the sine function for h in terms of t. Find the person’s height on the ride at t = 10 s. Find the first time, in seconds, that a person is 6 m above the ground. 4. 5. 8

Another Ferris Wheel Ride [cont’d] a) The period is 32 s. b) The centre of the Ferris wheel is 10 m off the ground. c) The equation, using the sine function for h in terms of t, is d) The height of the person when t = 10 is = 13. 4 m because e) Using the graph and tracing, the person is 6 m above the ground after 5. 63 s. 4. 5. 9

Suggested Questions: Pages 225 -227 1 -5 odd, 6 -15, 18, 20, 22 4. 5. 8