Chapter 4 Trigonometric Functions 4 2 Trigonometric Functions

Chapter 4 Trigonometric Functions 4. 2 Trigonometric Functions: The Unit Circle Copyright © 2014, 2010, 2007 Pearson Education, Inc. 1

Objectives: • Use a unit circle to define trigonometric functions of real numbers. • Recognize the domain and range of sine and cosine functions. • Find exact values of the trigonometric functions at • Use even and odd trigonometric functions. • Recognize and use fundamental identities. • Use periodic properties. • Evaluate trigonometric functions with a calculator. Copyright © 2014, 2010, 2007 Pearson Education, Inc. 2

The Unit Circle A unit circle is a circle of radius 1, with its center at the origin of a rectangular coordinate system. The equation of this circle is Copyright © 2014, 2010, 2007 Pearson Education, Inc. 3

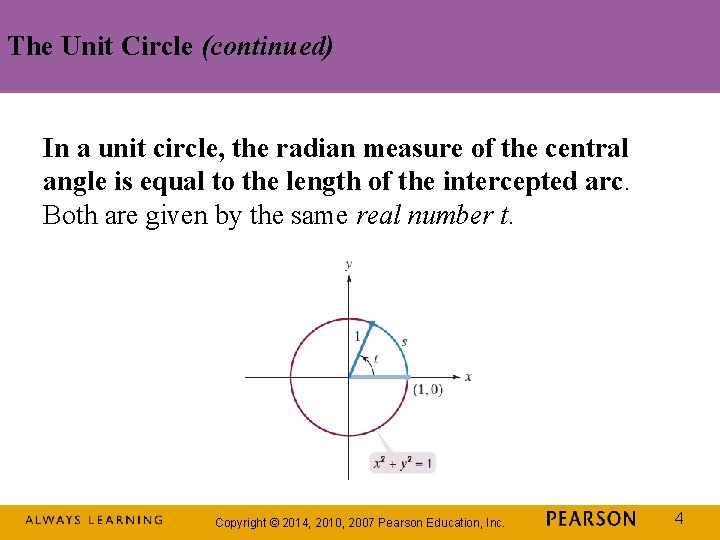
The Unit Circle (continued) In a unit circle, the radian measure of the central angle is equal to the length of the intercepted arc. Both are given by the same real number t. Copyright © 2014, 2010, 2007 Pearson Education, Inc. 4

The Six Trigonometric Functions Copyright © 2014, 2010, 2007 Pearson Education, Inc. 5

Definitions of the Trigonometric Functions in Terms of a Unit Circle Copyright © 2014, 2010, 2007 Pearson Education, Inc. 6

Example: Finding Values of the Trigonometric Functions Use the figure to find the values of the trigonometric functions at t. Copyright © 2014, 2010, 2007 Pearson Education, Inc. 7

Example: Finding Values of the Trigonometric Functions Use the figure to find the values of the trigonometric functions at t. Copyright © 2014, 2010, 2007 Pearson Education, Inc. 8

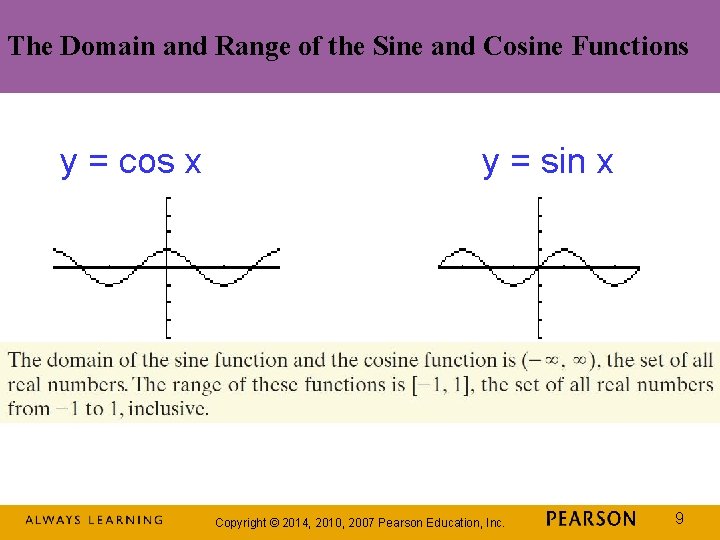
The Domain and Range of the Sine and Cosine Functions y = cos x y = sin x Copyright © 2014, 2010, 2007 Pearson Education, Inc. 9

Exact Values of the Trigonometric Functions at Trigonometric functions at occur frequently. We use the unit circle to find values of the trigonometric functions at We see that point P = (a, b) lies on the line y = x. Thus, point P has equal x- and y-coordinates: a = b. Copyright © 2014, 2010, 2007 Pearson Education, Inc. 10

Exact Values of the Trigonometric Functions at (continued) We find these coordinates as follows: Copyright © 2014, 2010, 2007 Pearson Education, Inc. 11

Exact Values of the Trigonometric Functions at (continued) We have used the unit circle to find the coordinates of point P = (a, b) that correspond to Copyright © 2014, 2010, 2007 Pearson Education, Inc. 12

Example: Finding Values of the Trigonometric Functions at Find Copyright © 2014, 2010, 2007 Pearson Education, Inc. 13

Example: Finding Values of the Trigonometric Functions at Find Copyright © 2014, 2010, 2007 Pearson Education, Inc. 14

Trigonometric Functions at Copyright © 2014, 2010, 2007 Pearson Education, Inc. 15

Even and Odd Trigonometric Functions Copyright © 2014, 2010, 2007 Pearson Education, Inc. 16

Example: Using Even and Odd Functions to Find Values of Trigonometric Functions Find the value of each trigonometric function: Copyright © 2014, 2010, 2007 Pearson Education, Inc. 17

Fundamental Identities Copyright © 2014, 2010, 2007 Pearson Education, Inc. 18

Example: Using Quotient and Reciprocal Identities Given and find the value of each of the four remaining trigonometric functions. Copyright © 2014, 2010, 2007 Pearson Education, Inc. 19

Example: Using Quotient and Reciprocal Identities (continued) Given and find the value of each of the four remaining trigonometric functions. Copyright © 2014, 2010, 2007 Pearson Education, Inc. 20

The Pythagorean Identities Copyright © 2014, 2010, 2007 Pearson Education, Inc. 21

Example: Using a Pythagorean Identity Given that and find the value of using a trigonometric identity. Copyright © 2014, 2010, 2007 Pearson Education, Inc. 22

Definition of a Periodic Function Copyright © 2014, 2010, 2007 Pearson Education, Inc. 23

Periodic Properties of the Sine and Cosine Functions Copyright © 2014, 2010, 2007 Pearson Education, Inc. 24

Periodic Properties of the Tangent and Cotangent Functions Copyright © 2014, 2010, 2007 Pearson Education, Inc. 25

Example: Using Periodic Properties Find the value of each trigonometric function: Copyright © 2014, 2010, 2007 Pearson Education, Inc. 26

Repetitive Behavior of the Sine, Cosine, and Tangent Functions Copyright © 2014, 2010, 2007 Pearson Education, Inc. 27

Using a Calculator to Evaluate Trigonometric Functions To evaluate trigonometric functions, we will use the keys on a calculator that are marked SIN, COS, and TAN. Be sure to set the mode to degrees or radians, depending on the function that you are evaluating. You may consult the manual for your calculator for specific directions for evaluating trigonometric functions. Copyright © 2014, 2010, 2007 Pearson Education, Inc. 28

Example: Evaluating Trigonometric Functions with a Calculator Use a calculator to find the value to four decimal places: Copyright © 2014, 2010, 2007 Pearson Education, Inc. 29