Transformations of the Graphs of Sine and Cosine





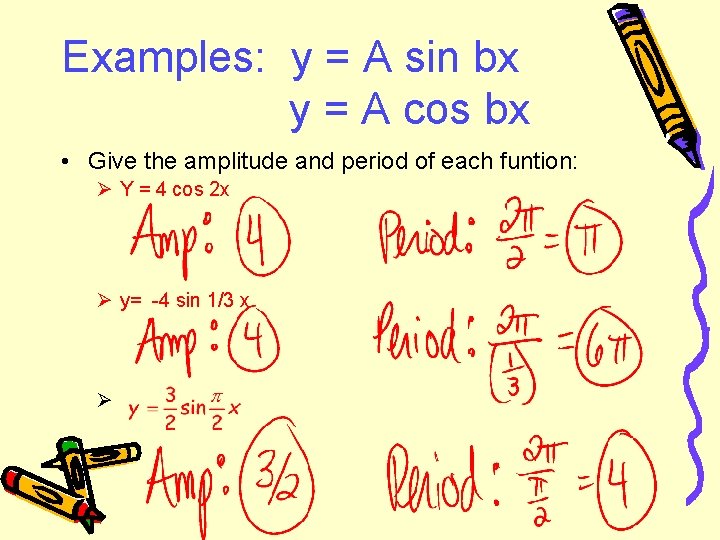

- Slides: 17

Transformations of the Graphs of Sine and Cosine Functions Credit to: JMerrill, 2010 EQ: How do I transform the graphs of trigonometric functions?

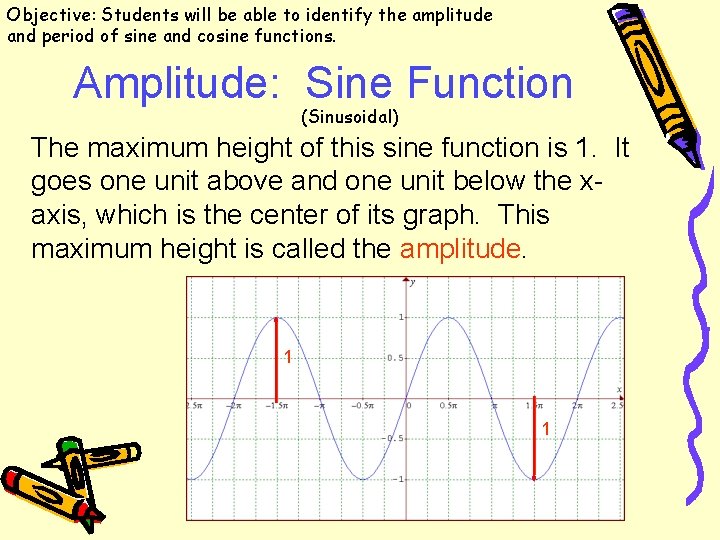
Objective: Students will be able to identify the amplitude and period of sine and cosine functions. Amplitude: Sine Function (Sinusoidal) The maximum height of this sine function is 1. It goes one unit above and one unit below the xaxis, which is the center of its graph. This maximum height is called the amplitude. 1 1

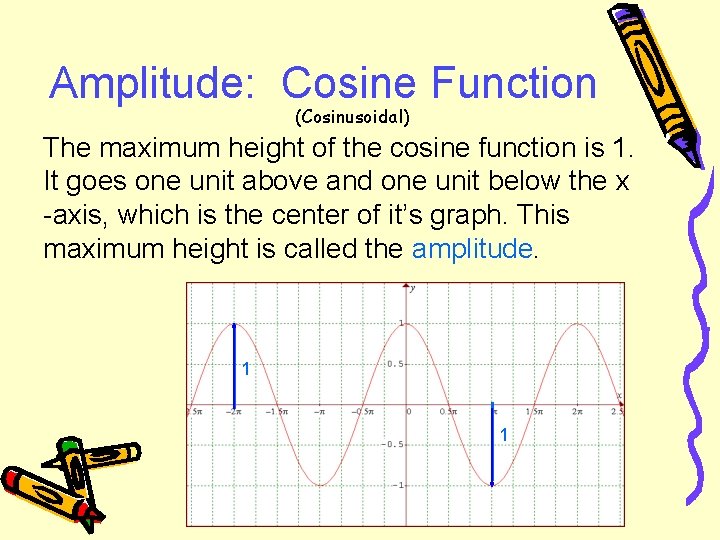
Amplitude: Cosine Function (Cosinusoidal) The maximum height of the cosine function is 1. It goes one unit above and one unit below the x -axis, which is the center of it’s graph. This maximum height is called the amplitude. 1 1

Amplitude The amplitude of the normal sine or cosine function is 1. To change the amplitude of a sine or cosine function, you would need to vertically stretch or compress the function. amplitude = ½|Max - Min| How to find: Choose the horizontal line that is dead-center of the graph. The amplitude has the same height above the center line (axis of the wave) as the height below the center line.

Examples: What is the amplitude? Vertical ______ by a factor of ___ Amp: ____

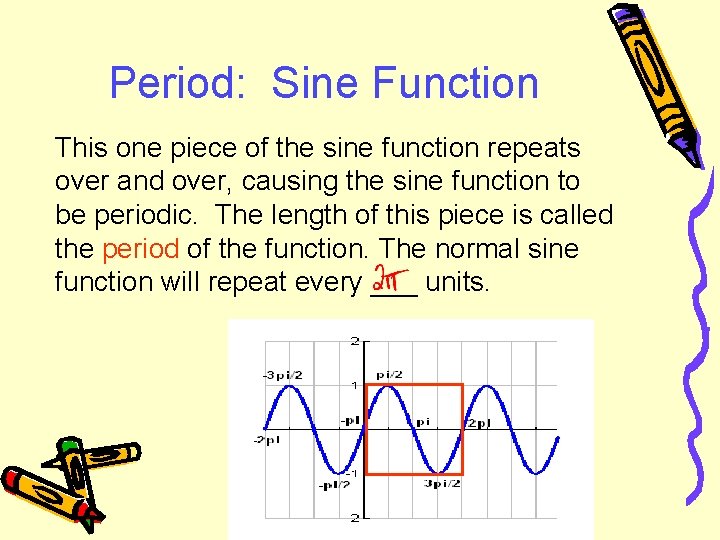
Period: Sine Function This one piece of the sine function repeats over and over, causing the sine function to be periodic. The length of this piece is called the period of the function. The normal sine function will repeat every ___ units.

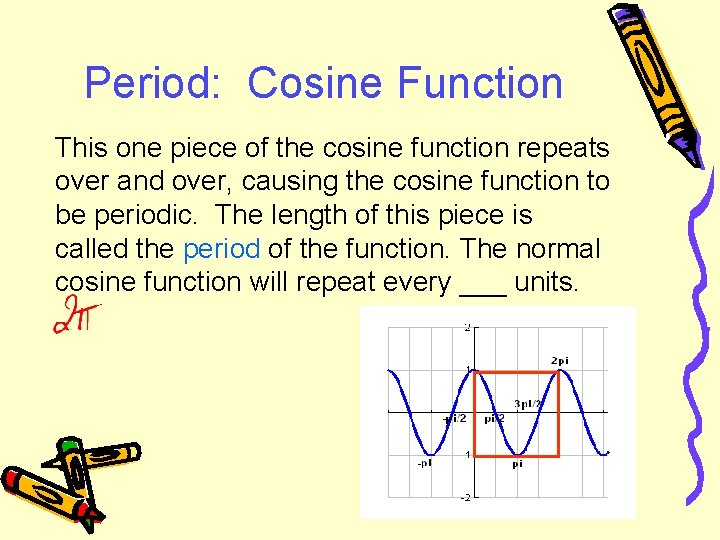
Period: Cosine Function This one piece of the cosine function repeats over and over, causing the cosine function to be periodic. The length of this piece is called the period of the function. The normal cosine function will repeat every ___ units.

Period Therefore, the period of a normal sine or cosine function is 2π. To change the period of a sine or cosine function, you would need to horizontally stretch or compress the function. The period is found by: period = In the equation, b affects the frequency, which is related to the period.

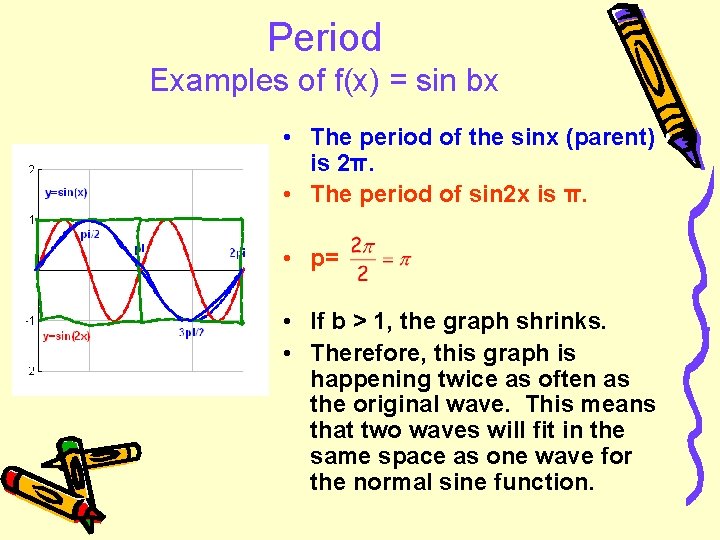
Period Examples of f(x) = sin bx • The period of the sinx (parent) is 2π. • The period of sin 2 x is π. • p= • If b > 1, the graph shrinks. • Therefore, this graph is happening twice as often as the original wave. This means that two waves will fit in the same space as one wave for the normal sine function.

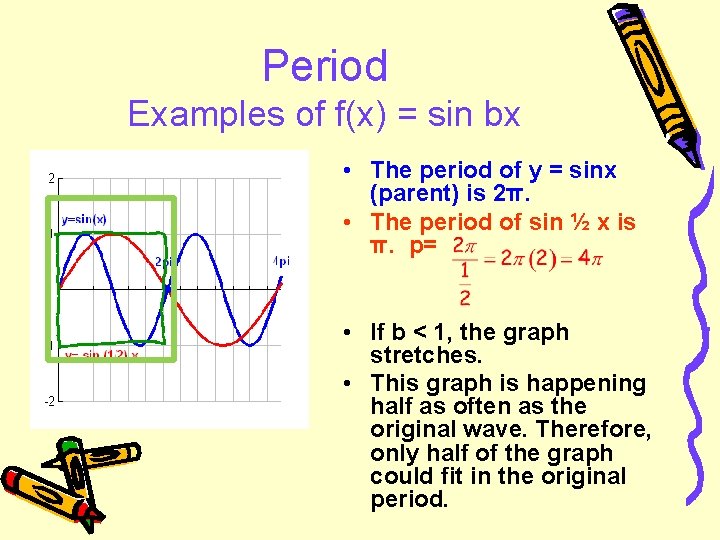
Period Examples of f(x) = sin bx • The period of y = sinx (parent) is 2π. • The period of sin ½ x is π. p= • If b < 1, the graph stretches. • This graph is happening half as often as the original wave. Therefore, only half of the graph could fit in the original period.

What is the period? Examples Horizontal ______ by a factor of ___ Per: ____
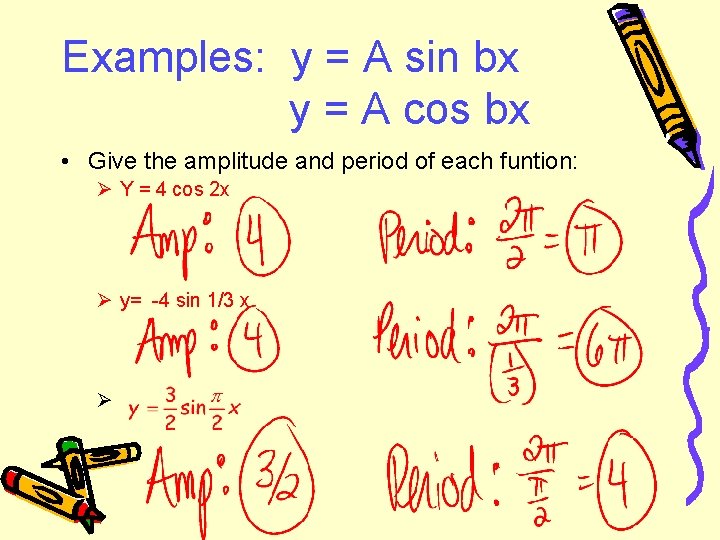
Examples: y = A sin bx y = A cos bx • Give the amplitude and period of each funtion: Ø Y = 4 cos 2 x Ø y= -4 sin 1/3 x Ø

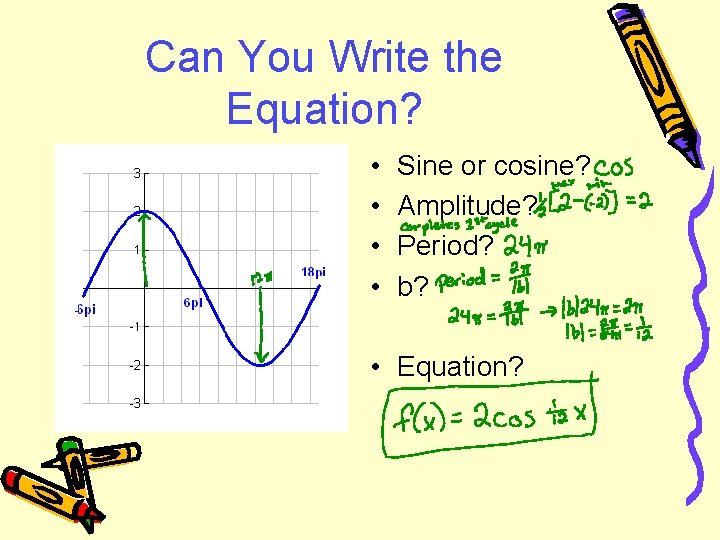
Can You Write the Equation? • • Sine or cosine? Amplitude? Period? b? • Equation?

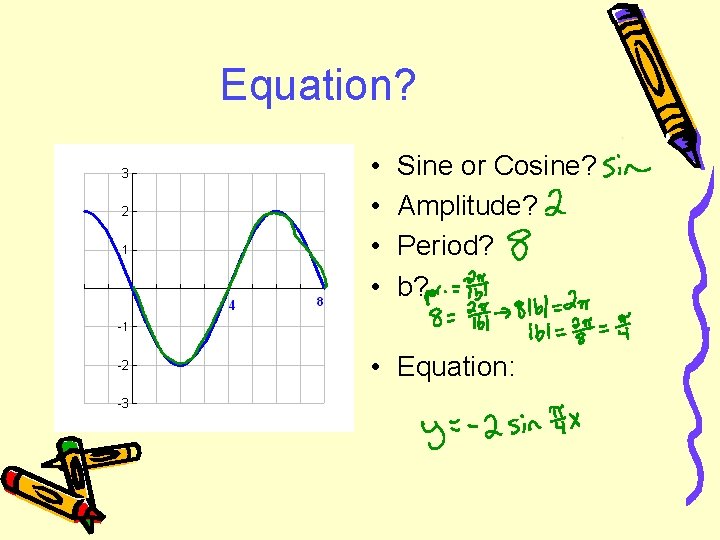
Equation? • • Sine or Cosine? Amplitude? Period? b? • Equation:

Graphing: Find the Critical points • To find the critical intervals (max/min, intercepts)

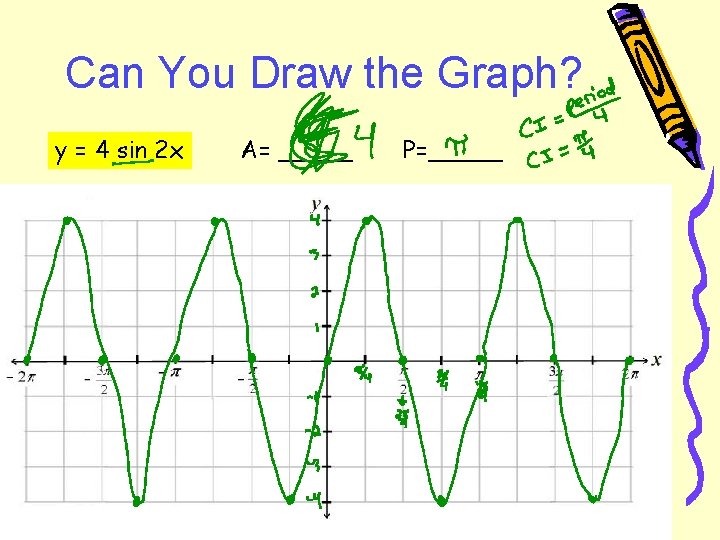
Can You Draw the Graph? y = 4 sin 2 x A= _____ P=_____

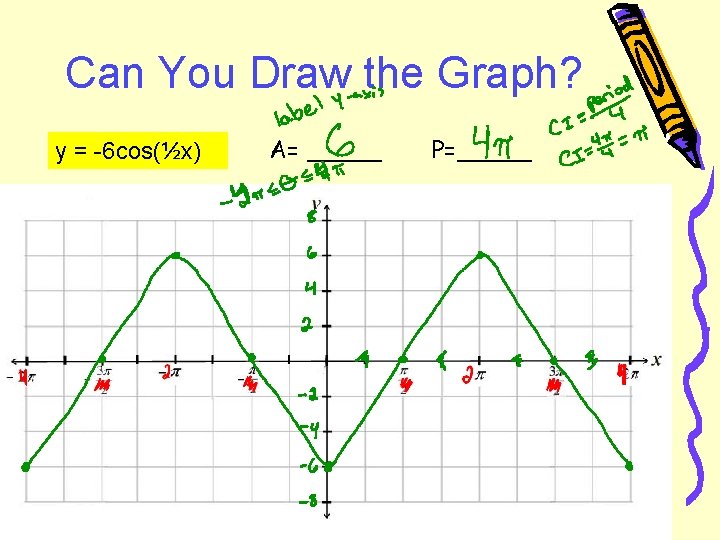
Can You Draw the Graph? y = -6 cos(½x) A= _____ P=_____
 Transformation of trigonometric functions
Transformation of trigonometric functions Cos wave formula
Cos wave formula Transformations of sine and cosine functions
Transformations of sine and cosine functions Graph transformations
Graph transformations How to find period from sine graph
How to find period from sine graph Tangent ratio geometry
Tangent ratio geometry Sine and cosine rule
Sine and cosine rule Sine maze
Sine maze Soh cah toa rules
Soh cah toa rules Graphing sine and cosine functions quiz
Graphing sine and cosine functions quiz When to use cosine rule
When to use cosine rule Sinusoids lesson 4-4 answer key
Sinusoids lesson 4-4 answer key Cos 1/2
Cos 1/2 Sine and cosine rules
Sine and cosine rules Cosine function graph equation
Cosine function graph equation Sine cosine tangent word problems
Sine cosine tangent word problems Sine cosine tangent
Sine cosine tangent Burj khalifa trigonometry
Burj khalifa trigonometry