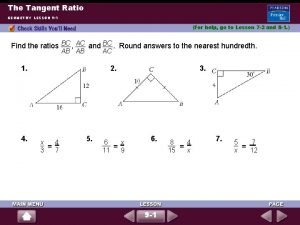
4 5 Graphs of Sine and Cosine Functions

4. 5 Graphs of Sine and Cosine Functions You’ll need graph paper

Unit Circle Activity On Graph paper use a radius of 7 in to represent the radius of your unit circle. ¡ Then give both the fractional and decimal value of your trig function for each value of theta on the unit circle. (Do not include the last value of theta for your quadrant) i. e. 90, 180, 270, 360 ¡ 2

12 Groups 1 -4 – Sine ¡ Groups 5 -8 – Cosine ¡ Groups 9 -12 – Tangent ne o eed n ly On group per h p gra ¡ Group ¡ 4 n+1 4 n+2 4 n+3 4 n+4 – – Q 1 Q 2 Q 3 Q 4 n is a whole # Ex: Group 7: 7 = 4(1)+3 Cosine Q 3 3

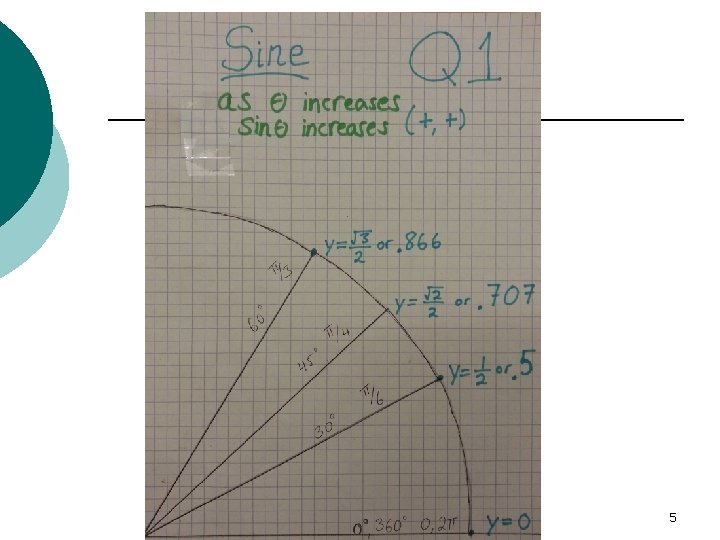
Label with “as increases, [trigfunction( )] increases/decreases. ” ¡ Ex for sine of Q 1: ¡ l “as increases, increases. ” 4

5

to ng i s t d r ee ta s n s i e one wn! y n r ryo e Eve heir o e v E t sin h do wit Graph the sine and cosine functions ¡ ¡ Graph the sine function on a new piece of graph paper Label your x-axis in radians in multiples of. Use 1 square for each measure 13 squares on each side of y-axis ¡ On your y-axis label 1 square as ¼. . Count 8 squares on each side of x-axis ¡ Then graph the cosine function a separate axis. (use the same labels) 6

Graph the csc and sec functions ¡ ¡ Graph csc with the sin graph and sec with the cos graph Then make a new graph for tan and cot l Label your x-axis in radians in multiples of 7

Ordered Pairs Consider the values for x and y in the table to the right ¡ Note ¡ l l l Period = 2π Maximum y values Minimum y values x sin(x) cos(x) -3. 1416 0. 0000 -1. 0000 -2. 6180 -0. 5000 -0. 8660 -2. 0944 -0. 8660 -0. 5000 -1. 5708 -1. 0000 0. 0000 -1. 0472 -0. 8660 0. 5000 -0. 5236 -0. 5000 0. 8660 0. 0000 1. 0000 0. 5236 0. 5000 0. 8660 1. 0472 0. 8660 0. 5000 1. 5708 1. 0000 0. 0000 2. 0944 0. 8660 -0. 5000 2. 6180 0. 5000 -0. 8660 3. 1416 0. 0000 -1. 0000 3. 6652 -0. 5000 -0. 8660 4. 1888 -0. 8660 -0. 5000 4. 7124 -1. 0000 0. 0000 5. 2360 -0. 8660 0. 5000 5. 7596 -0. 5000 0. 8660 6. 2832 0. 0000 1. 0000 8

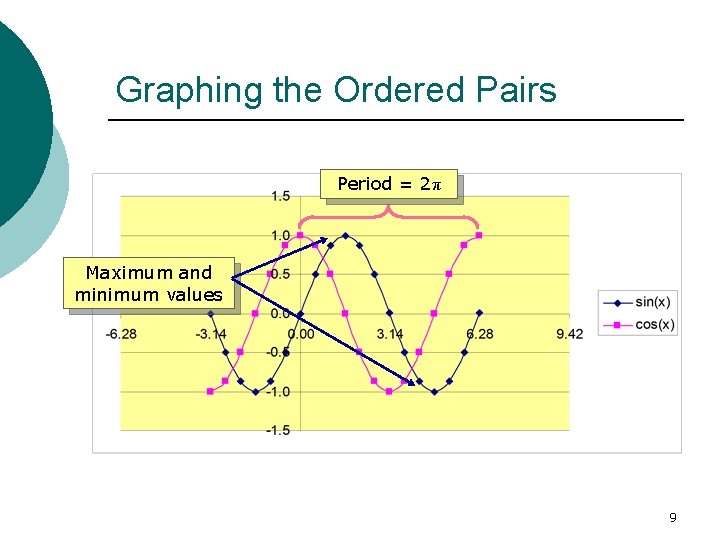
Graphing the Ordered Pairs Period = 2π Maximum and minimum values 9

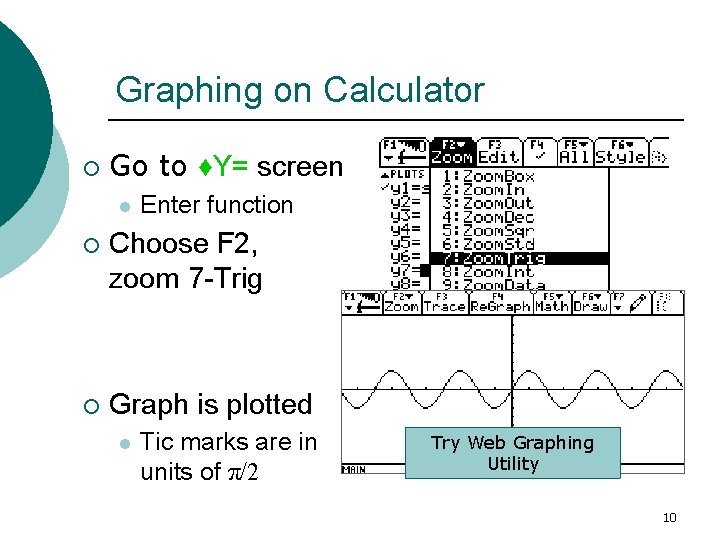
Graphing on Calculator ¡ Go to ♦Y= screen l Enter function ¡ Choose F 2, zoom 7 -Trig ¡ Graph is plotted l Tic marks are in units of π/2 Try Web Graphing Utility 10

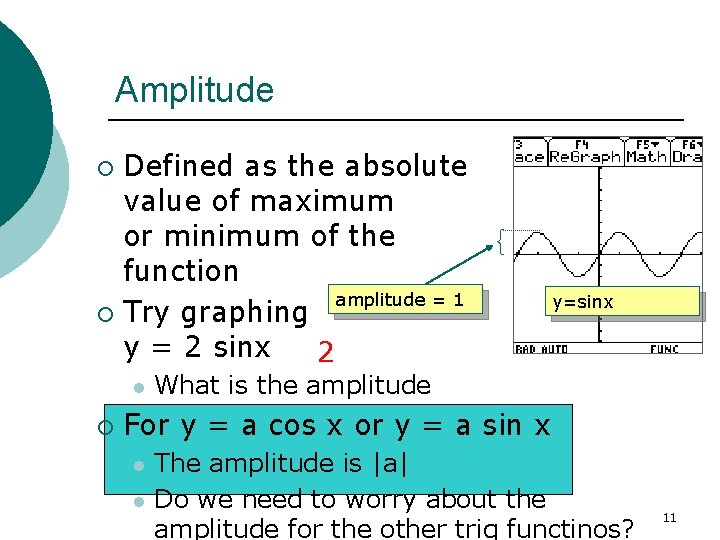
Amplitude Defined as the absolute value of maximum or minimum of the function amplitude = 1 ¡ Try graphing y = 2 sinx 2 ¡ l ¡ y=sinx What is the amplitude For y = a cos x or y = a sin x l l The amplitude is |a| Do we need to worry about the amplitude for the other trig functinos? 11

Period of a Trig Function (Recall slide from previous lesson) The functions repeat themselves ¡ The period is the smallest value, p for which f(x) = f(x + p) ¡ For sin, cos, sec, csc ¡ l ¡ The period is 2π For tan and cot l The period is π 12

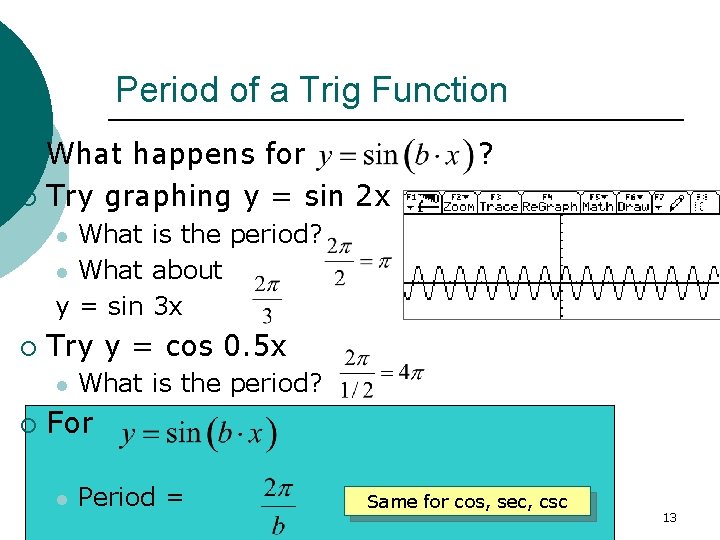
Period of a Trig Function What happens for ¡ Try graphing y = sin 2 x ¡ ? What is the period? l What about y = sin 3 x l ¡ Try y = cos 0. 5 x l ¡ What is the period? For l Period = Same for cos, sec, csc 13

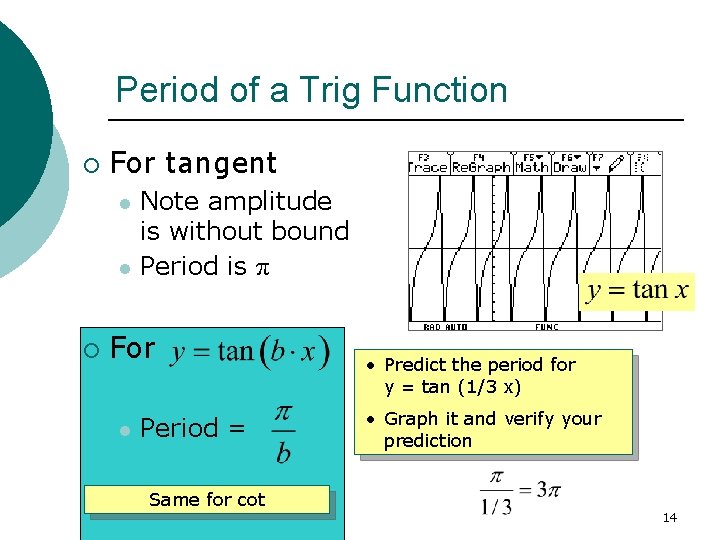
Period of a Trig Function ¡ For tangent l l ¡ Note amplitude is without bound Period is π For l Period = Same for cot • Predict the period for y = tan (1/3 x) • Graph it and verify your prediction 14

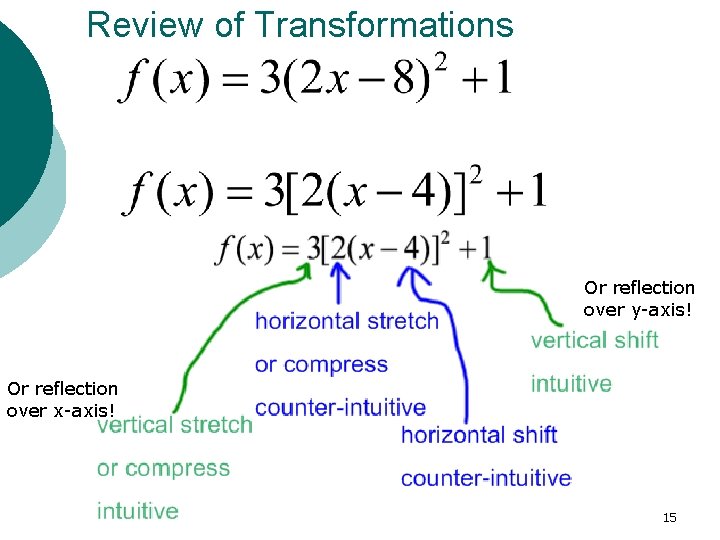
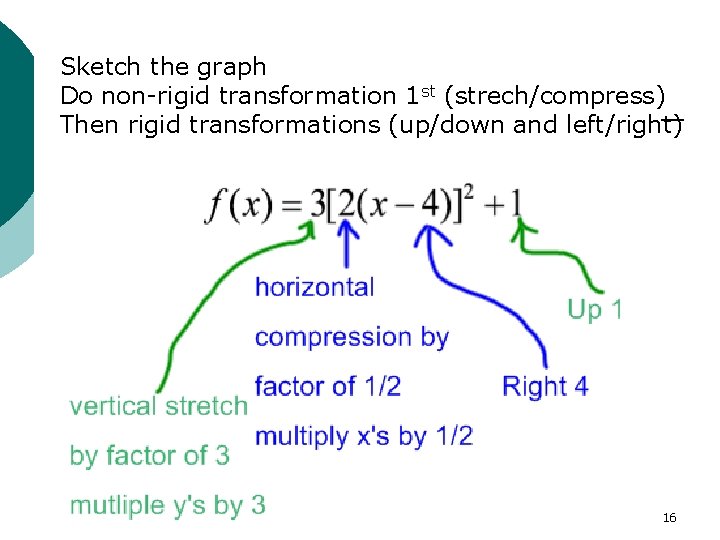
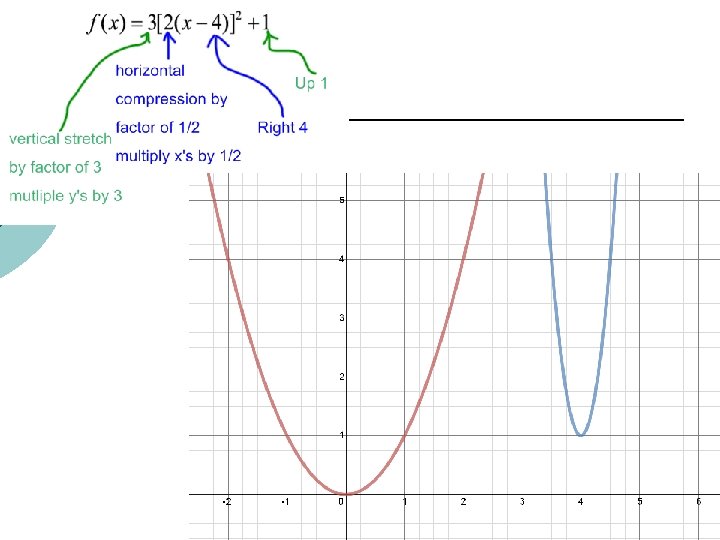
Review of Transformations Or reflection over y-axis! Or reflection over x-axis! 15

Sketch the graph Reviewtransformation of Transformations Do non-rigid 1 st (strech/compress) Then rigid transformations (up/down and left/right) 16

17

Let’s investigate with graphs of trig functions! Desmos. com 18

Practice time ¡ Graph Sketch each transformation of the graph a. Sketch between 0 and 2 pi while doing transformations b. Does the make a difference? 19

H Dub ¡ 4 -5 Pg 328 #1 -25 odd, 35 -51 EOO 20

Graph the sine and cosine functions Regraph the sine and cosine functions on two separate axis ¡ Label your graph in radians ¡ ¡ ¡ On your y-axis label Leave room above and below! On your x-axis label multiples of 21