The Tangent Ratio GEOMETRY LESSON 9 1 For

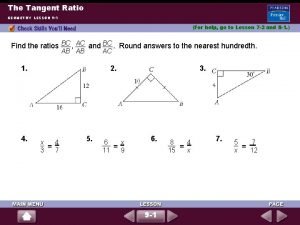
The Tangent Ratio GEOMETRY LESSON 9 -1 (For help, go to Lesson 7 -3 and 8 -1. ) BC , AC and BC. Round answers to the nearest hundredth. Find the ratios AB AB AC 1. 4. 2. x 4 = 3 7 5. 6 x = 11 9 3. 6. 9 -1 8 4 = 15 x 7. 5 7 = x 12

The Tangent Ratio GEOMETRY LESSON 9 -1 Solutions 1. Use the Pythagorean Theorem to find AB: a 2 + b 2 = c 2 (12)2 + (16)2 = AB 2 144 + 256 = AB 2 = 400 AB = 400 = 20; B�C 12 substitute 20 for AB, 16 for AC, and 12 for BC; = = 0. 60; AB 20 A�C 16 B�C 12 = = 0. 80; = = 0. 75 AB AC 16 20 2. BC = 10; use the Pythagorean Theorem to find AB: a 2 + b 2 = c 2 (10)2 + (10)2 = AB 2 100 + 100 = AB 2 = 200 AB = 200 = 10 2; substitute 10 2 for AB, 10 for AC, and 10 for BC; BC 10 A�C 10 B�C 10 = 0. 71; = = 1 AB 10 2 AC 10 3. AC = 4; The triangle is a 30 -60°-90° triangle, so the sides opposite the angles in order are in the ratio 1 : 3 : 2. BC is AC 3 = 4 3, and BC 4 3 3 AB = 2 AC = 2(4) = 8; By substitution, = 0. 87; AB 1 B�C 4 3 = = = 0. 5; = 3 1. 73 AB 8 2 AC 4 A�C 4 9 -1 8 2

The Tangent Ratio GEOMETRY LESSON 9 -1 Solutions (continued) x 4 4 3 12 5 4. Multiply both sides of = by 3: x = • = or 1 3 7 7 1 7 7 6 x 6 9 54 10 5. Multiply both sides of = by 9: x = • = or 4 11 8 15 4 x 5 x 7 12 9 11 11 6. = ; (8)x = (4)(15)(Cross Products); simplify: 8 x = 60; 60 8 15 2 divide by 8: x = = or 7 1 2 7. = ; (5)(12) = (7)x (Cross Products); simplify: 60 = 7 x; 60 divide by 7: x = or 8 7 4 7 9 -1

The Tangent Ratio GEOMETRY LESSON 9 -1 Write the tangent ratios for A and B. tan A = 20 opposite BC = = 21 adjacent AC tan B = opposite AC 21 = = adjacent BC 20 9 -1

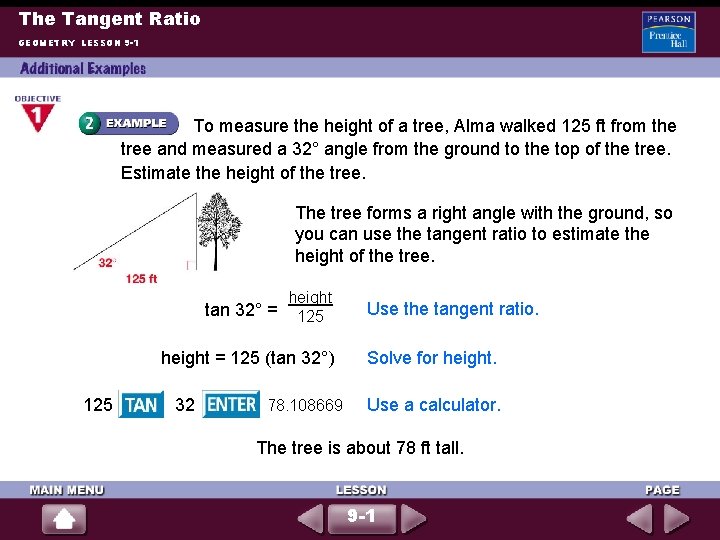
The Tangent Ratio GEOMETRY LESSON 9 -1 To measure the height of a tree, Alma walked 125 ft from the tree and measured a 32° angle from the ground to the top of the tree. Estimate the height of the tree. The tree forms a right angle with the ground, so you can use the tangent ratio to estimate the height of the tree. height tan 32° = 125 height = 125 (tan 32°) 125 32 78. 108669 Use the tangent ratio. Solve for height. Use a calculator. The tree is about 78 ft tall. 9 -1

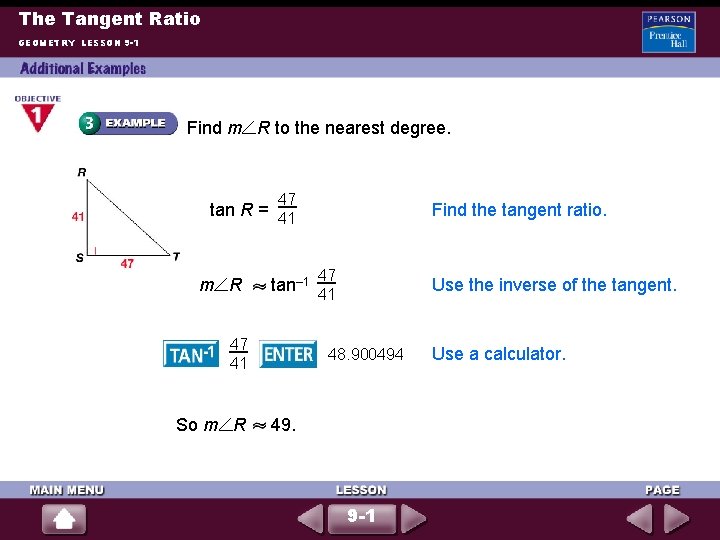
The Tangent Ratio GEOMETRY LESSON 9 -1 Find m R to the nearest degree. 47 tan R = 41 m R tan– 1 47 41 Find the tangent ratio. 47 41 Use the inverse of the tangent. 48. 900494 So m R 49. 9 -1 Use a calculator.

The Tangent Ratio GEOMETRY LESSON 9 -1 Pages 472 -475 Exercises 1. 1 ; 2 2 9. 21. 4 17. 74. 1 2. 2 3 ; 10. About 50 yd 18. 13. 5 3. 1; 1 11. 32 19. 114. 5 4. 11. 2 5. 12. 3 12. 58 13. 48 20. 89. 4 21. 44 and 136 6. 14. 4 14. 65 22. 52 m 7. 2. 5 15. 63 8. 1. 6 16. 58 23. Answers may vary. Sample: 5, 12, 13; 22. 6 and 67. 4 3 2 9 -1

The Tangent Ratio GEOMETRY LESSON 9 -1 24. Consider a 30 -60 -90 . Let the length of the shorter side be a. Then the length of the longer side, opposite the 60° , is a 3. Thus, tan a 3 60° = = 3. a 2 25. 2 = 1, so we have – 1 to show tan 1 = 45°. Consider a 45 -45 -90 . Let the lengths of the shorter sides be a. Thus, tan 45° = a = 1. 30. a. 0. 1; 0. 2; 0. 3; 0. 4; 0. 5; 0. 6; 0. 7; 0. 8; 1; 1. 2; 1. 4; 1. 7; 2. 1; 2. 7; 3. 7; 5. 7; 11. 4 b. a 26. 152° and 28° 27. w = 5; x = 4. 7 28. w = 6. 7; x = 8. 1 c. 29. w = 59; x = 36 9 -1 approaches 0; increases to infinity

The Tangent Ratio GEOMETRY LESSON 9 -1 30. (continued) d. Answers may vary. Samples: 82; 2. 5; 74 37. 45. 0 44. a. No; answers may vary. Sample: tan 45° + tan 30° 1 + 0. 6 = 1. 6, but tan(45 + 30)° = tan 75° 3. 7 b. No; Assume tan A° – tan B° = tan(A – B)°, or tan A° = tan B° + tan (A – B)°. Let A = B + C, so by subst. , tan(B + C)° = tan B° + tan C°. This is false by part (a). 38. 30. 0 39. 22. 4 31. about 51° 40. 10. 4 32. about 701 ft 41. 6. 0 33. about 296 ft 42. 3. 5 34. about 58. 4% 43. 1. 6 35. 71. 6 36. 60. 0 9 -1

The Tangent Ratio GEOMETRY LESSON 9 -1 45. a. 57. 290 b. 572. 96 c. Answers may vary. Sample: tan X° 572, 958 for X° 89. 9999 d. Answers may vary. Sample: 45. (continued) d. In a rt. , as an acute approaches 90°, the opp. side gets longer. 46. a. Every Y 1 value = 1. b. The graph is that of Y 1 = 1. c. Conjecture: tan x° • tan(90 – x) = 1. 46. (continued) c. Proof: Let x be an acute measure in a rt. . Then the other acute measures (90 – x). So tan x° = opp. , and tan adj. (90 – x)° = . opp. Therefore, tan x° • tan(90 – x)° = opp. • adj. = 1 adj. 9 -1 opp.

The Tangent Ratio GEOMETRY LESSON 9 -1 47. 42 55. 78. 7 63. 118. 1 48. 75 56. 53. 1 64. 19. 6 49. 6 57. 36. 9 65. 82. 4 50. 50 58. 33. 7 66. 900 cm 2 51. x 59. 9. 5 67. obtuse 60. 60 68. acute 53. 26. 6 61. 12. 2 69. right 54. 80. 5 62. 29. 0 70. R(a, b); S(a, –b); T(c, –b); V(c, b) 52. m X 9 -1

The Tangent Ratio GEOMETRY LESSON 9 -1 Use the figure for Exercises 1– 3. 1. Write the tangent ratio for K. 15 8 2. Write the tangent ratio for M. 8 15 3. Find m M to the nearest degree. 28 Find x to the nearest whole number. 4. 5. 29 52 9 -1

Sine and Cosine Ratios GEOMETRY LESSON 9 -2 (For help, go to Lesson 9 -1. ) For each triangle, find (a) the length of the leg opposite B and (b) the length of the leg adjacent to B. 1. 2. 3. 9 -2

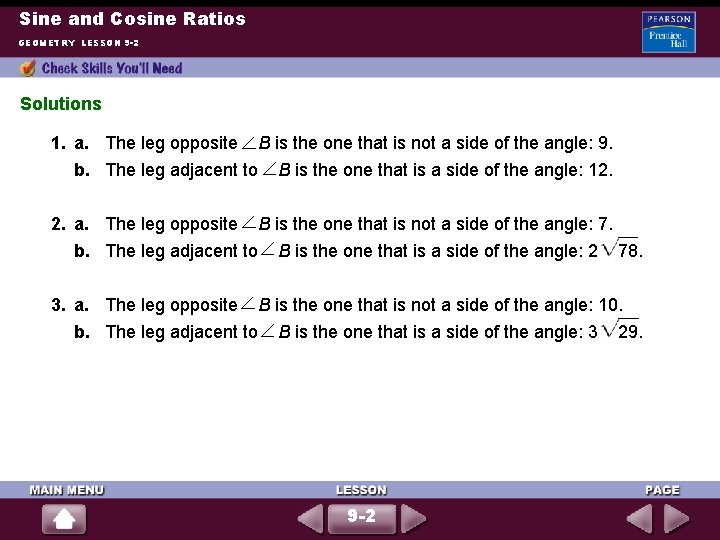
Sine and Cosine Ratios GEOMETRY LESSON 9 -2 Solutions 1. a. The leg opposite B is the one that is not a side of the angle: 9. b. The leg adjacent to B is the one that is a side of the angle: 12. 2. a. The leg opposite B is the one that is not a side of the angle: 7. b. The leg adjacent to B is the one that is a side of the angle: 2 78. 3. a. The leg opposite B is the one that is not a side of the angle: 10. b. The leg adjacent to B is the one that is a side of the angle: 3 29. 9 -2

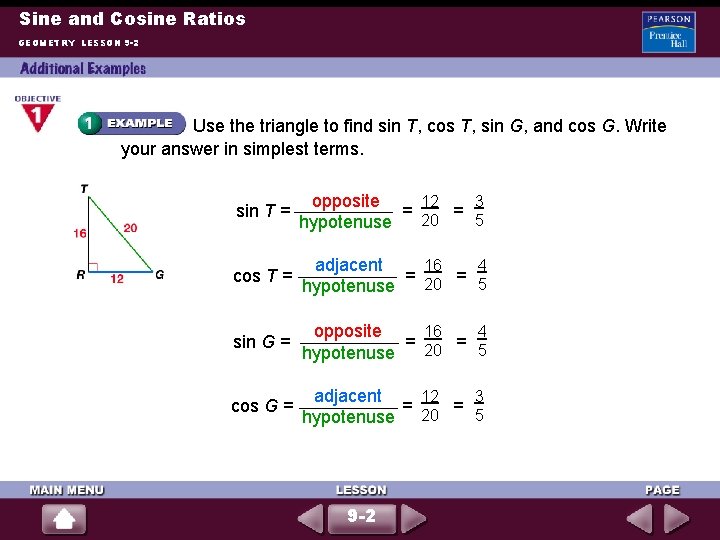
Sine and Cosine Ratios GEOMETRY LESSON 9 -2 Use the triangle to find sin T, cos T, sin G, and cos G. Write your answer in simplest terms. sin T = 12 3 opposite = 20 = 5 hypotenuse cos T = 16 4 adjacent = 20 = 5 hypotenuse sin G = 4 opposite 16 = 20 = 5 hypotenuse cos G = 3 adjacent 12 = 20 = 5 hypotenuse 9 -2

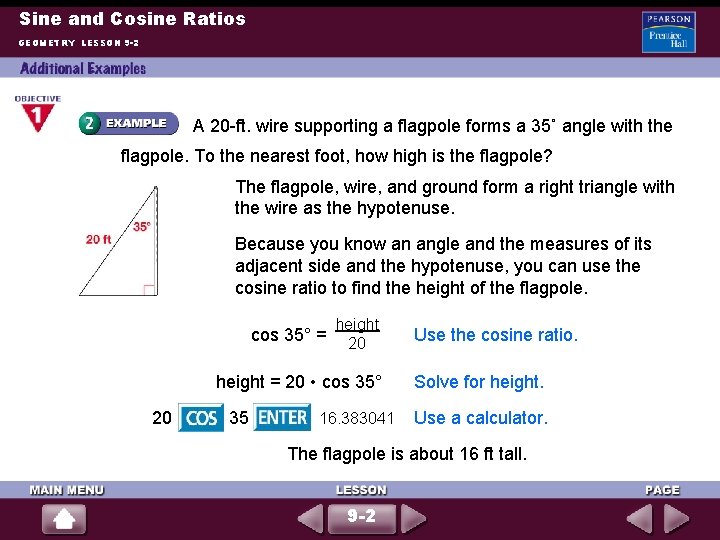
Sine and Cosine Ratios GEOMETRY LESSON 9 -2 A 20 -ft. wire supporting a flagpole forms a 35˚ angle with the flagpole. To the nearest foot, how high is the flagpole? The flagpole, wire, and ground form a right triangle with the wire as the hypotenuse. Because you know an angle and the measures of its adjacent side and the hypotenuse, you can use the cosine ratio to find the height of the flagpole. cos 35° = height 20 height = 20 • cos 35° 20 35 16. 383041 Use the cosine ratio. Solve for height. Use a calculator. The flagpole is about 16 ft tall. 9 -2

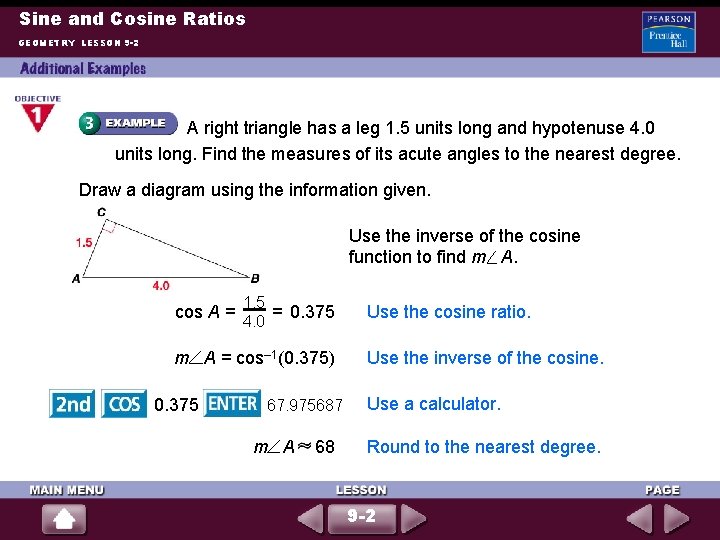
Sine and Cosine Ratios GEOMETRY LESSON 9 -2 A right triangle has a leg 1. 5 units long and hypotenuse 4. 0 units long. Find the measures of its acute angles to the nearest degree. Draw a diagram using the information given. Use the inverse of the cosine function to find m A. 1. 5 cos A = 4. 0 = 0. 375 Use the cosine ratio. m A = cos– 1(0. 375) Use the inverse of the cosine. 0. 375 67. 975687 m A 68 Use a calculator. Round to the nearest degree. 9 -2

Sine and Cosine Ratios GEOMETRY LESSON 9 -2 (continued) To find m B, use the fact that the acute angles of a right triangle are complementary. m A + m B = 90 68 + m B 90 Definition of complementary angles Substitute. m B 22 The acute angles, rounded to the nearest degree, measure 68 and 22. 9 -2

Sine and Cosine Ratios GEOMETRY LESSON 9 -2 Pages 479 -481 Exercises 1. 7 24 ; 25 25 9. 106. 5 17. about 17 ft 8 in. 2. 4 2 7 ; 10. 1085 ft 18. sin X ÷ cos X = 3. 4. 9 9 1 3 ; 2 2 11. 21 = tan X 5. 8. 3 12. 51 13. 46 6. 17. 9 14. 59 19. cos X • tan X = opp. adj. opp. • = hyp. adj. = sin X 7. 17. 0 15. 24 20. sin X ÷ tan X = 8. 11. 5 opp. adj. opp. ÷ = hyp. adj. hyp. 4. 3 opp. adj. ÷ = hyp. adj. hyp. 16. 66 = cos X 9 -2

Sine and Cosine Ratios GEOMETRY LESSON 9 -2 s 21. No; the are ~ and the sine ratio for 35° is constant. 22. w = 3; x = 41. 4 23. w = 37; x = 7. 5 24. w = 68. 3; x = 151. 6 25. a. They are equal; yes; the sine and cosine of complementary s are =. b. B; A c. Answers may vary. Sample: cosine of A = sine of the compl. of A. 26. a. 2 2 b. 2 2 c. 2 2 9 -2 d. 2 2 e. They are equal. 27. Yes; use any trig. function and the known measures to find one other side. Use the Pythagorean Thm. to find the 3 rd side. Subtract the acute measure from 90 to get the other measure.

Sine and Cosine Ratios GEOMETRY LESSON 9 -2 28. a. 3 2 b. 1 2 c. 1 2 d. 3 2 e. cos 30° = 3 sin 30° f. sin 60° = 3 cos 60° 29. (continued) opp. Since sin A = , hyp. if sin A ≥ 1, then opp. ≥ hyp. , which is impossible. hyp. approaches 1. 30. a. 0. 99985 31. (sin A)2 + (cos A)2 = b-d. Answers may vary, samples are given. b. 1. 29. Answers may vary. Sample: s d. For that approach 90, the opp. side gets close to the hyp. opp. in length, so c. sin X = 1 for X = 89. 9; no 9 -2 2 a + = b 2 c c a 2 + = b 2 c 2 c 2 a 2 + b 2 = = 1 c 2

Sine and Cosine Ratios GEOMETRY LESSON 9 -2 32. (sin B)2 + (cos B)2 = b 2 a 2 + = c c b 2 a 2 + = c 2 b 2 + a 2 = c 2 = 1 c 2 33. 1 – (tan A)2 = (cos A)2 b 2 a 2 1 ÷ – = 2 2 c b c 2 + a 2 c 2 – = a 2 b 2 b 2 = 1 b 2 1 1 1 34. 1 2 – = – = (sin A) a 2 b (tan A)2 a 2 c 2 – b 2 c 2 – = = 1 b 2 a 2 a 2 2 2 a a 35. (tan A)2 – (sin A)2 = – = – = 2 2 2 b c 2(c 2 – b 2) 2 c 2 2 b 2 2 c 2 – a 2 b 2 a a – = b 2 c 2 b c 2 2 2(sin A)2 a 2 • a a 2 = (tan A) b 2 • c 2 c b 36. a. about 1. 5 AU b. about 5. 2 AU 9 -2

Sine and Cosine Ratios GEOMETRY LESSON 9 -2 37. A 38. H 40. (continued) [1] one angle found correctly 39. A 41. 6. 9 40. [2] a. cos G = 7 42. 3. 3 10 m G = cos– 1 ≈ 46 7 10 b. m R ≈ 90 – 46 = 44 OR m R = 7 ≈ 44 sin– 1 10 43. 18 44. 12. 9 ft or 4. 9 ft 45. (36 + 18 3) cm 2 46. 42. 5 in 2 47. 30 3 mm 2 9 -2

Sine and Cosine Ratios GEOMETRY LESSON 9 -2 Use this figure for Exercises 1 and 2. 1. Write the ratios for sin A and sin B. 8 16 30 15 sin A = or , sin B = or 17 34 34 17 2. Write the ratios for cos A and cos B. 8 30 15 16 cos A = or , cos B = or 34 Use this figure for Exercises 3 and 4. 17 34 3. Find x to the nearest tenth. 21. 0 4. Find y to the nearest tenth. 13. 6 Use this figure for Exercises 5 and 6. 5. Find x to the nearest degree. 44 6. Find y to the nearest degree. 46 9 -2 17

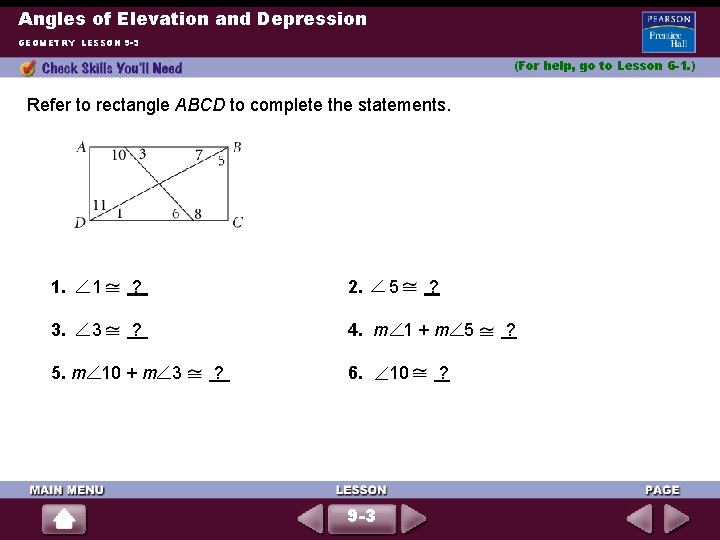
Angles of Elevation and Depression GEOMETRY LESSON 9 -3 (For help, go to Lesson 6 -1. ) Refer to rectangle ABCD to complete the statements. 1 ? 2. 3 ? 4. m 1 + m 5 5. m 10 + m 3 ? 6. 9 -3 5 ? 10 ? ?

Angles of Elevation and Depression GEOMETRY LESSON 9 -3 Solutions 1. Since all rectangles are parallelograms, AB || DC. By the Alternate Interior Angles Theorem, 1 7. 2. Since all rectangles are parallelograms, AD || BC. By the Alternate Interior Angles Theorem, 5 11. 3. Since all rectangles are parallelograms, AB || DC. By the Alternate Interior Angles Theorem, 3 6. 4. Since ABCD is a rectangle, each of its angles measures 90. So, BDC is a right triangle with m C = 90. The sum of the angles of a triangle is 180, so m 1 + m 5 + m C = 180; substitute for m C: m 1 + m 5 + 90 = 180; subtract 90 from each side: m 1 + m 5 = 90. 5. 10 and 3 form a straight angle so their sum is 180. 6. Since all rectangles are parallelograms, AB || DC. By the Alternate Interior Angles Theorem, 10 8. 9 -3

Angles of Elevation and Depression GEOMETRY LESSON 9 -3 Describe 1 and 2 as they relate to the situation shown. One side of the angle of depression is a horizontal line. 1 is the angle of depression from the airplane to the building. One side of the angle of elevation is a horizontal line. 2 is the angle of elevation from the building to the airplane. 9 -3

Angles of Elevation and Depression GEOMETRY LESSON 9 -3 A surveyor stands 200 ft from a building to measure its height with a 5 -ft tall theodolite. The angle of elevation to the top of the building is 35°. How tall is the building? Draw a diagram to represent the situation. tan 35° = x 200 Use the tangent ratio. x = 200 • tan 35° 200 35 140. 041508 Solve for x. Use a calculator. So x 140. To find the height of the building, add the height of the Theodolite, which is 5 ft tall. The building is about 140 ft + 5 ft, or 145 ft tall. 9 -3

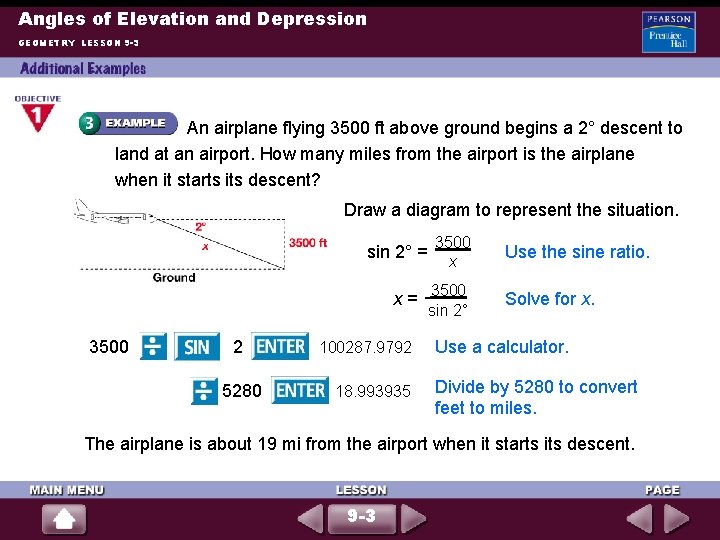
Angles of Elevation and Depression GEOMETRY LESSON 9 -3 An airplane flying 3500 ft above ground begins a 2° descent to land at an airport. How many miles from the airport is the airplane when it starts its descent? Draw a diagram to represent the situation. sin 2° = x = 3500 2 5280 100287. 9792 18. 993935 3500 x 3500 sin 2° Use the sine ratio. Solve for x. Use a calculator. Divide by 5280 to convert feet to miles. The airplane is about 19 mi from the airport when it starts its descent. 9 -3

Angles of Elevation and Depression GEOMETRY LESSON 9 -3 Pages 484 -488 Exercises 1. of elevation from sub to boat 6. of elevation from Kelley to waterfall 13. about 986 m 14. 51. 3 ft 2. of depression from boat to sub 7. of depression from waterfall to Jim 3. of elevation from boat to lighthouse 8. of depression from waterfall to Kelley 4. of depression from lighthouse to boat 9. 34. 2 ft 10. 502. 4 m 5. of elevation from Jim to waterfall 15. 777. 9 m 16. 263. 3 yd 17. 0. 6 km 18. 769 ft 19. 64° 11. 32. 2 m 20. 4. 8° 12. 86. 6 ft 9 -3

Angles of Elevation and Depression GEOMETRY LESSON 9 -3 21. about 194 m 22. a-b Check students’ work. 23. 3300 m 24. 72, 72 25. 46, 46 28. (continued) b. about 15. 9° 29. a. Length of any guy wire = dist. on the ground from tower to the guy wire div. by the cosine of the formed by the guy wire and the ground. 29. (continued) b. Height of attachment = dist. on the ground from tower to the guy wire times the tangent of the formed by the guy wire and the ground. 26. 27, 27 30. 5 27. 20, 20 31. about 2. 8 28. a. 560 ft 32. 0. 5; about 84. 9 9 -3

Angles of Elevation and Depression GEOMETRY LESSON 9 -3 33. 370 m 36. Check students’ work. 34. about 28 ft 37. C 35. Measure the length of the stick and the shortest shadow. The tangent of the angle of elevation is the ratio of the length of the stick to the length of the shadow. Then use inverse tangent. 38. F 44. [2] a. 39. B 40. A b. Let h represent the height of the tree. h ≈ 6 + 12 tan 83º h ≈ 6 + 12(8. 14) ≈ 6 + 98 = 104 The tree is about 104 ft tall. 41. C 42. A 43. C 9 -3

Angles of Elevation and Depression GEOMETRY LESSON 9 -3 44. [1] correct drawing OR correct solution without work shown 51. 130 52. 240 53. 230 45. 85. 2 m 54. x = 9; 60, 30, 40, 30 46. 38. 2 ft 47. 45 55. y = 3, x = 2; 16, 10, 16 48. 70 49. 110 50. 60 9 -3

Angles of Elevation and Depression GEOMETRY LESSON 9 -3 Use the diagram for Exercises 1 and 2. 1. Describe how 1 relates to the situation. angle of elevation from man’s eyes to treetop 2. Describe how 2 relates to the situation. angle of depression from treetop to man’s eyes A 6 -ft man stands 12 ft from the base of a tree. The angle of elevation from his eyes to the top of the tree is 76°. 3. About how tall is the tree? about 54 ft 4. If the man releases a pigeon that flies directly to the top of the tree, about how far will it fly? about 50 ft 5. What is the angle of depression from the treetop to the man’s eyes? 76° 9 -3

Vectors GEOMETRY LESSON 9 -4 (For help, go to Lesson 7 -2. ) Find the value of x. 1. 2. 3. 9 -4

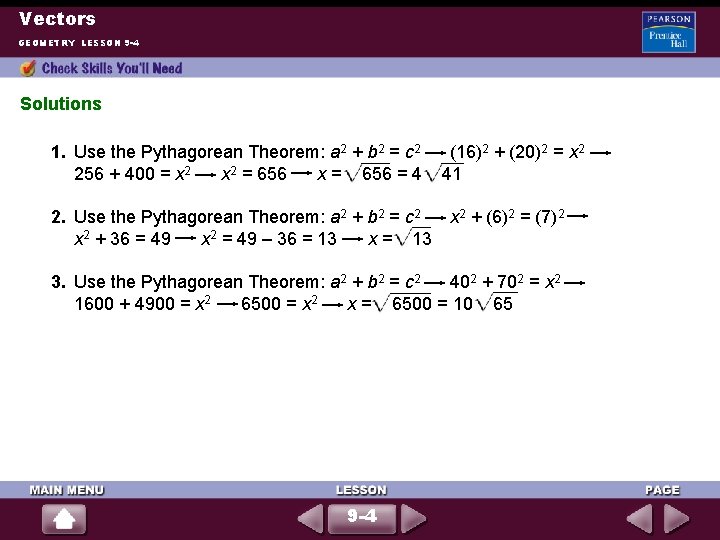
Vectors GEOMETRY LESSON 9 -4 Solutions 1. Use the Pythagorean Theorem: a 2 + b 2 = c 2 (16)2 + (20)2 = x 2 256 + 400 = x 2 = 656 x = 656 = 4 41 2. Use the Pythagorean Theorem: a 2 + b 2 = c 2 x 2 + (6)2 = (7)2 x 2 + 36 = 49 x 2 = 49 – 36 = 13 x = 13 3. Use the Pythagorean Theorem: a 2 + b 2 = c 2 402 + 702 = x 2 1600 + 4900 = x 2 6500 = x 2 x = 6500 = 10 65 9 -4

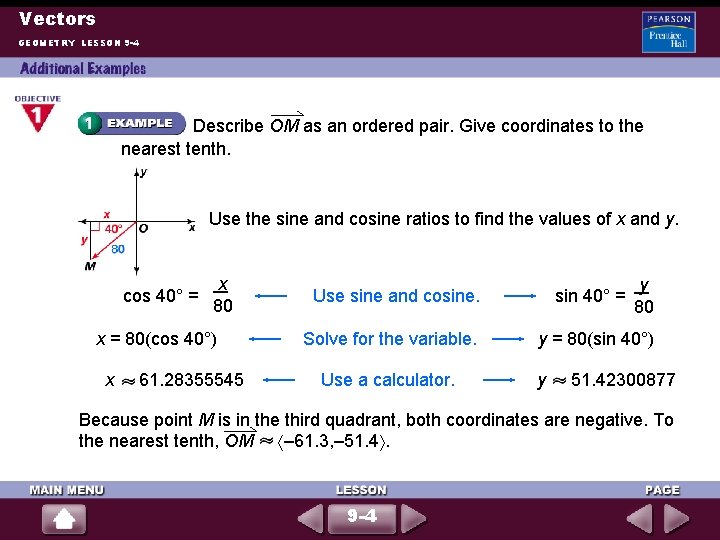
Vectors GEOMETRY LESSON 9 -4 Describe OM as an ordered pair. Give coordinates to the nearest tenth. Use the sine and cosine ratios to find the values of x and y. cos 40° = x 80 x = 80(cos 40°) x 61. 28355545 Use sine and cosine. y sin 40° = 80 Solve for the variable. y = 80(sin 40°) Use a calculator. y 51. 42300877 Because point M is in the third quadrant, both coordinates are negative. To the nearest tenth, OM – 61. 3, – 51. 4. 9 -4

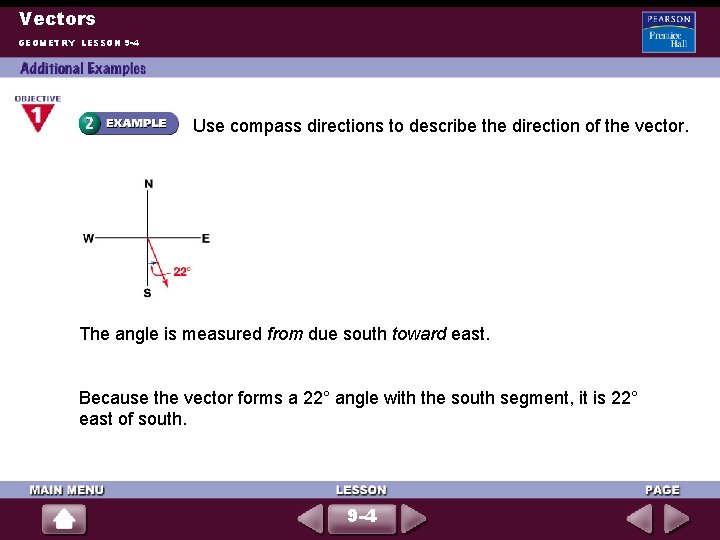
Vectors GEOMETRY LESSON 9 -4 Use compass directions to describe the direction of the vector. The angle is measured from due south toward east. Because the vector forms a 22° angle with the south segment, it is 22° east of south. 9 -4

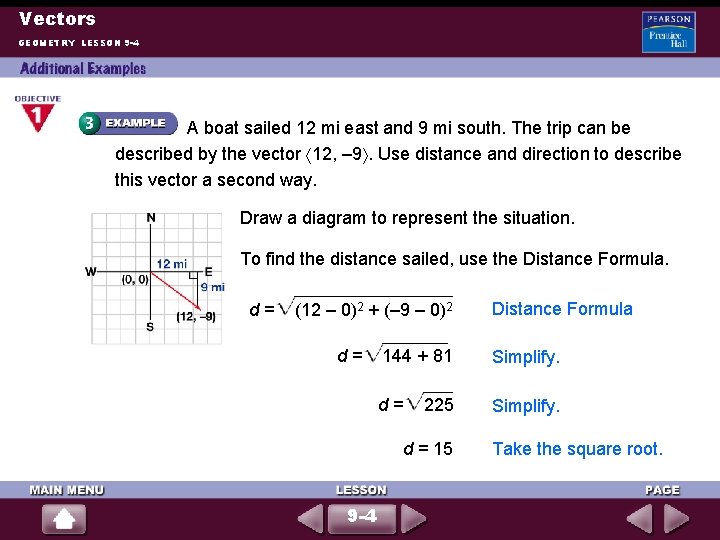
Vectors GEOMETRY LESSON 9 -4 A boat sailed 12 mi east and 9 mi south. The trip can be described by the vector 12, – 9. Use distance and direction to describe this vector a second way. Draw a diagram to represent the situation. To find the distance sailed, use the Distance Formula. d = (12 – 0)2 + (– 9 – 0)2 Distance Formula d = 144 + 81 Simplify. d = 225 Simplify. d = 15 9 -4 Take the square root.

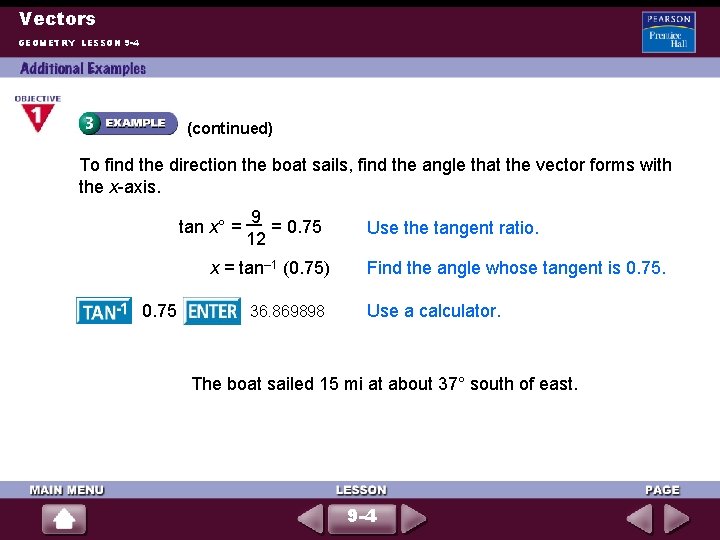
Vectors GEOMETRY LESSON 9 -4 (continued) To find the direction the boat sails, find the angle that the vector forms with the x-axis. 9 tan x° = = 0. 75 12 x = tan– 1 (0. 75) 0. 75 36. 869898 Use the tangent ratio. Find the angle whose tangent is 0. 75. Use a calculator. The boat sailed 15 mi at about 37° south of east. 9 -4

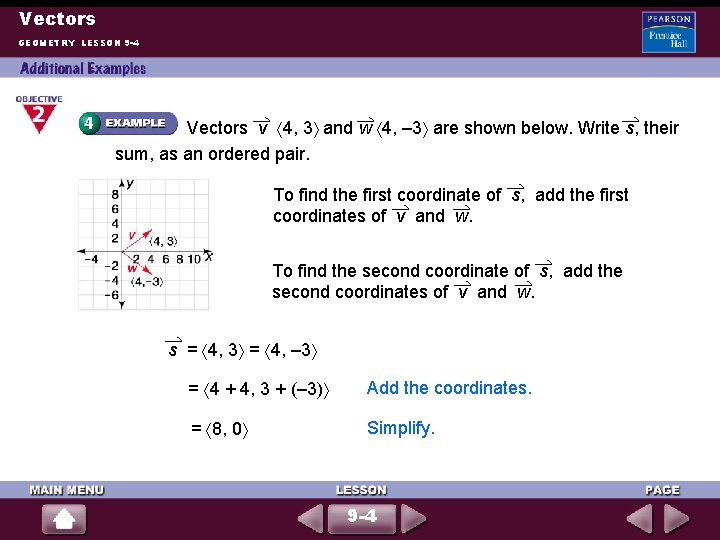
Vectors GEOMETRY LESSON 9 -4 Vectors v 4, 3 and w 4, – 3 are shown below. Write s, their sum, as an ordered pair. To find the first coordinate of s, add the first coordinates of v and w. To find the second coordinate of s, add the second coordinates of v and w. s = 4, 3 = 4, – 3 = 4 + 4, 3 + (– 3) Add the coordinates. = 8, 0 Simplify. 9 -4

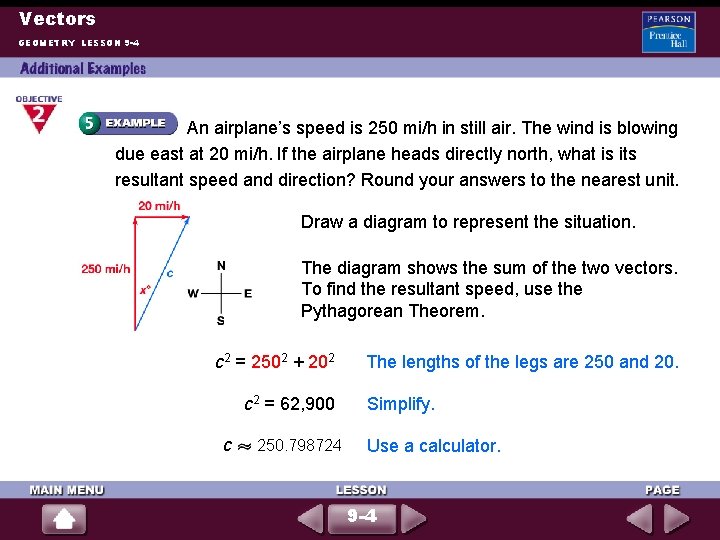
Vectors GEOMETRY LESSON 9 -4 An airplane’s speed is 250 mi/h in still air. The wind is blowing due east at 20 mi/h. If the airplane heads directly north, what is its resultant speed and direction? Round your answers to the nearest unit. Draw a diagram to represent the situation. The diagram shows the sum of the two vectors. To find the resultant speed, use the Pythagorean Theorem. c 2 = 2502 + 202 c 2 = 62, 900 c 250. 798724 The lengths of the legs are 250 and 20. Simplify. Use a calculator. 9 -4

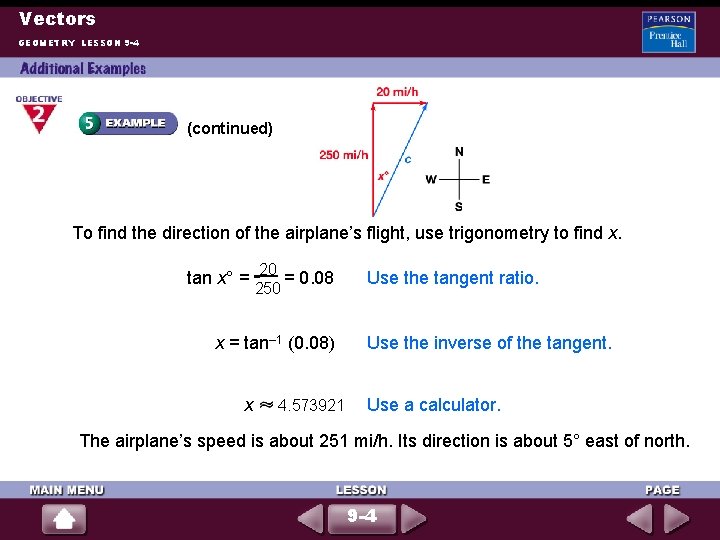
Vectors GEOMETRY LESSON 9 -4 (continued) To find the direction of the airplane’s flight, use trigonometry to find x. 20 tan x° = = 0. 08 250 x = tan– 1 (0. 08) x 4. 573921 Use the tangent ratio. Use the inverse of the tangent. Use a calculator. The airplane’s speed is about 251 mi/h. Its direction is about 5° east of north. 9 -4

Vectors GEOMETRY LESSON 9 -4 Pages 493 -497 Exercises 1. 602. 2, 668. 8 2. – 307. 3, – 54. 2 7. 10. 8. 11. 9. 12. 3. 37. 5, – 65. 0 4. 15° south of west 5. 20° west of south 6. 40° east of south 9 -4

Vectors GEOMETRY LESSON 9 -4 13. about 97 mi at 41° south of west 17. (continued) b. 19. a. – 1, 0 b. 14. about 707 mi; 65° south of west 15. about 54 mi/h; 22° north of east 16. 4805 km; 12° north of west 18. a. – 6, 2 20. a. 1, – 1 b. b. 17. a. – 9, – 9 9 -4

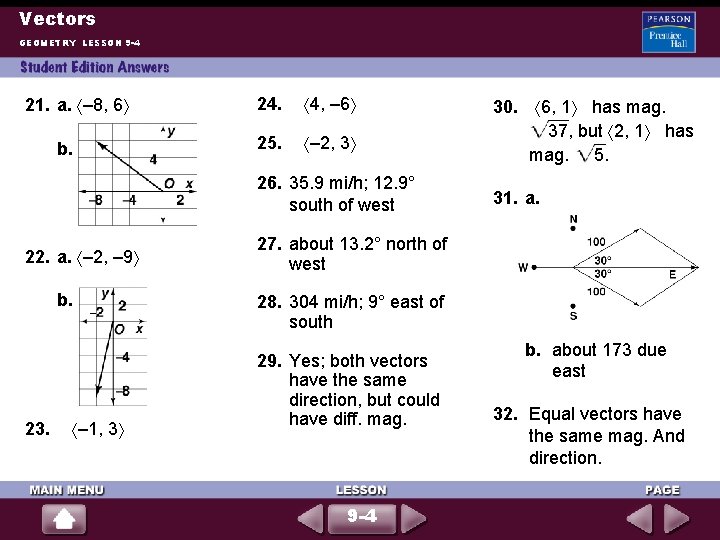
Vectors GEOMETRY LESSON 9 -4 21. a. – 8, 6 b. 24. 4, – 6 25. – 2, 3 26. 35. 9 mi/h; 12. 9° south of west 22. a. – 2, – 9 b. 23. – 1, 3 30. 6, 1 has mag. 37, but 2, 1 has mag. 5. 31. a. 27. about 13. 2° north of west 28. 304 mi/h; 9° east of south 29. Yes; both vectors have the same direction, but could have diff. mag. 9 -4 b. about 173 due east 32. Equal vectors have the same mag. And direction.

Vectors GEOMETRY LESSON 9 -4 33. Vectors are if they have the same or opp. directions. 34. (continued) b. 35. a. 0, 0 b. a and c have = mag. and opp. direction. 34. a. 36. about 386 mi/h at 148 south of west about 134 km at about 46. 6° south of east 9 -4 37. – 1 – 2 38. 11 – 5

Vectors GEOMETRY LESSON 9 -4 39. – 1 0 40. A. III B. II C. I 41. (continued) d. 471. 5 mi/h at 6. 3° south of east 44. 3, – 3 42. – 3, – 7 41. a. 45. The vectors have the same mag. ; the vectors have opp. directions. 43. 0, – 4 b. 530, 0 ; – 61. 3, – 51. 4 c. 468. 7, – 51. 4 9 -4

Vectors GEOMETRY LESSON 9 -4 46. Answers may vary. Sample: 7, 24 , – 7, 24 , 7, – 24 , 24, 7 47. a. about 15° south of west 49. about 2229 ft; about 10° 50. a. 2 3 b. Check students’ work b. about 6. 7 h 48. a. about 24. 1 mi; about 14. 1 mi b. about 28 mi at about 30° east of north 51. Answers may vary. Sample: zero vector = 0, 0 ; it has mag. 0 and no direction. 52. a. Yes; when you add integers, which are the coordinates of the vectors, order is not important. b. Yes; if the first two vectors are the same, but in opp. order. 53. D 54. [2] a. about 36 ft/min 9 -4

Vectors GEOMETRY LESSON 9 -4 54. [2] (continued) b. about 34° east of south [1]correct speed OR correct direction 55. [4] a. b. aircraft: 400, 0 wind: – 25, – 43. 3 55. [4] (continued) c. 375, – 43. 3 d. about 377 mi/h, 6. 6° south of east [3]appropriate methods, but with one computational error [2]correct speed of aircraft OR correct speed of wind 9 -4 55. (continued) [1] correct speed of aircraft OR correct speed of wind without work shown 56. 4492 ft 57. 1 8 58. 3 8 59. 1 3 60. 56 units 2

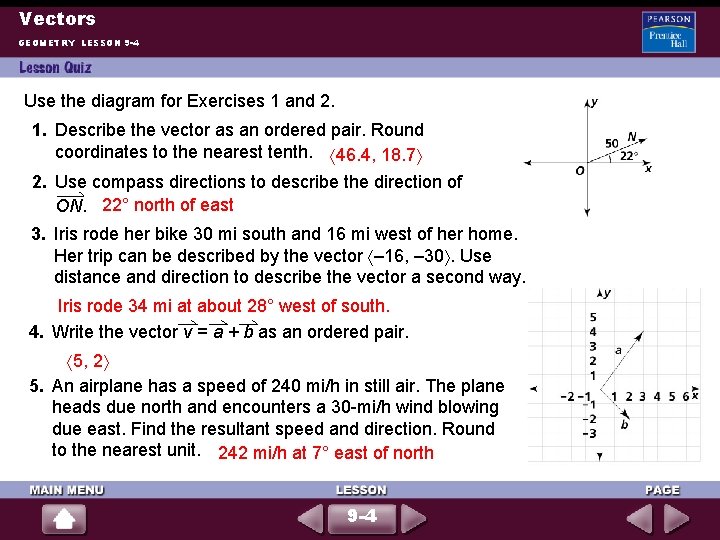
Vectors GEOMETRY LESSON 9 -4 Use the diagram for Exercises 1 and 2. 1. Describe the vector as an ordered pair. Round coordinates to the nearest tenth. 46. 4, 18. 7 2. Use compass directions to describe the direction of ON. 22° north of east 3. Iris rode her bike 30 mi south and 16 mi west of her home. Her trip can be described by the vector – 16, – 30. Use distance and direction to describe the vector a second way. Iris rode 34 mi at about 28° west of south. 4. Write the vector v = a + b as an ordered pair. 5, 2 5. An airplane has a speed of 240 mi/h in still air. The plane heads due north and encounters a 30 -mi/h wind blowing due east. Find the resultant speed and direction. Round to the nearest unit. 242 mi/h at 7° east of north 9 -4

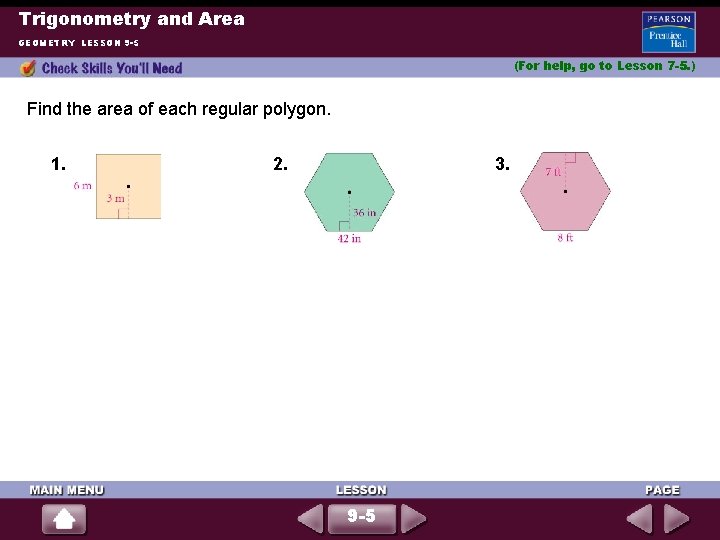
Trigonometry and Area GEOMETRY LESSON 9 -5 (For help, go to Lesson 7 -5. ) Find the area of each regular polygon. 1. 2. 3. 9 -5

Trigonometry and Area GEOMETRY LESSON 9 -5 Solutions 1. The perimeter is 4(6) = 24 m. The area A of a regular polygon is half the 1 1 2 apothem a times the perimeter p: A = ap = (3)(24) = 36 m 2 2 2. The perimeter is 6(42) = 252 in. The area A of a regular polygon is half 1 1 2 the apothem a times the perimeter p: A = ap = (36)(252) = 4536 in. 2 2 3. The perimeter is 6(8) = 48 ft. The area A of a regular polygon is half the 1 1 2 apothem a times the perimeter p: A = ap = (7)(48) = 168 ft 2 9 -5 2

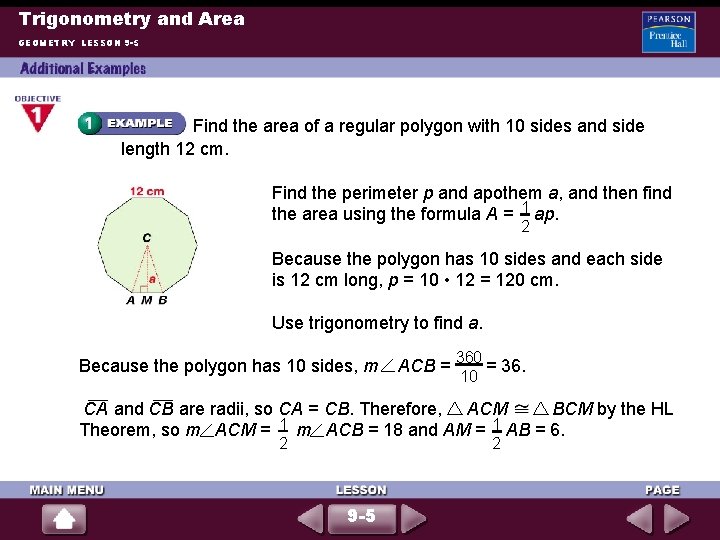
Trigonometry and Area GEOMETRY LESSON 9 -5 Find the area of a regular polygon with 10 sides and side length 12 cm. Find the perimeter p and apothem a, and then find 1 the area using the formula A = ap. 2 Because the polygon has 10 sides and each side is 12 cm long, p = 10 • 12 = 120 cm. Use trigonometry to find a. 360 Because the polygon has 10 sides, m ACB = = 36. 10 and CB are radii, so CA = CB. Therefore, ACM BCM by the HL CA 1 1 Theorem, so m ACM = m ACB = 18 and AM = AB = 6. 2 2 9 -5

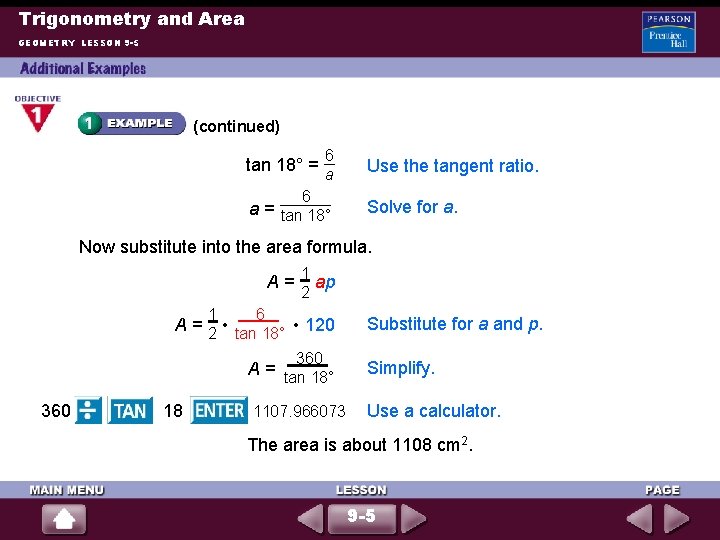
Trigonometry and Area GEOMETRY LESSON 9 -5 (continued) 6 a = tan 18° = Use the tangent ratio. Solve for a. Now substitute into the area formula. 1 A = ap 2 1 6 A = • • 120 2 tan 18° 360 18 Substitute for a and p. A = tan 18° Simplify. 1107. 966073 Use a calculator. The area is about 1108 cm 2. 9 -5

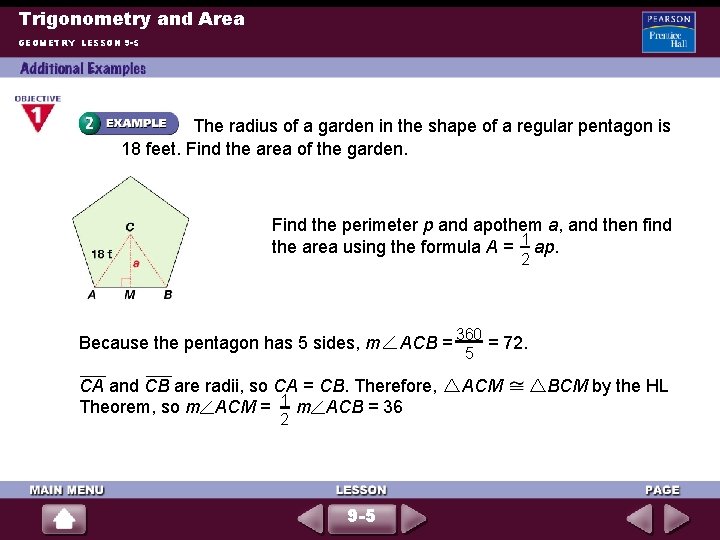
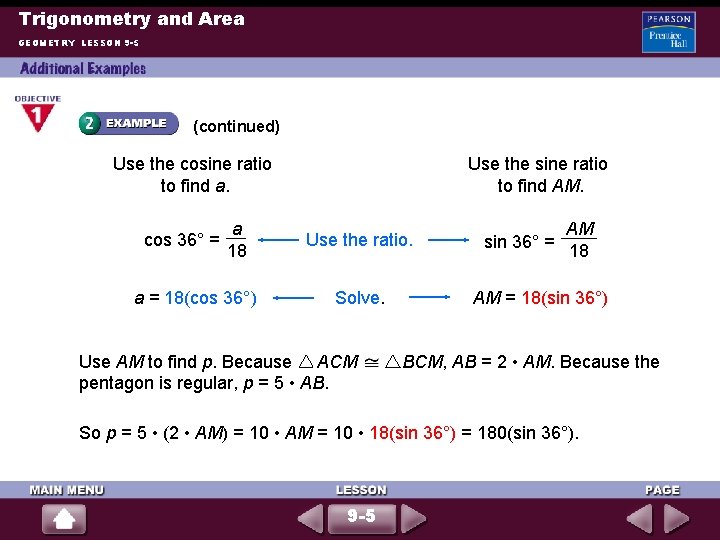
Trigonometry and Area GEOMETRY LESSON 9 -5 The radius of a garden in the shape of a regular pentagon is 18 feet. Find the area of the garden. Find the perimeter p and apothem a, and then find 1 the area using the formula A = ap. 2 360 Because the pentagon has 5 sides, m ACB = = 72. 5 CA and CB are radii, so CA = CB. Therefore, ACM BCM by the HL 1 Theorem, so m ACM = m ACB = 36 2 9 -5

Trigonometry and Area GEOMETRY LESSON 9 -5 (continued) Use the cosine ratio to find a. cos 36° = a 18 a = 18(cos 36°) Use the sine ratio to find AM. Use the ratio. Solve. sin 36° = AM 18 AM = 18(sin 36°) Use AM to find p. Because ACM BCM, AB = 2 • AM. Because the pentagon is regular, p = 5 • AB. So p = 5 • (2 • AM) = 10 • AM = 10 • 18(sin 36°) = 180(sin 36°). 9 -5

Trigonometry and Area GEOMETRY LESSON 9 -5 (continued) 1 Finally, substitute into the area formula A = ap. 2 1 2 A = • 18(cos 36°) • 180(sin 36°) Substitute for a and p. A = 1620(cos 36°) • (sin 36°) Simplify. A 770. 355778 Use a calculator. The area of the garden is about 770 ft 2. 9 -5

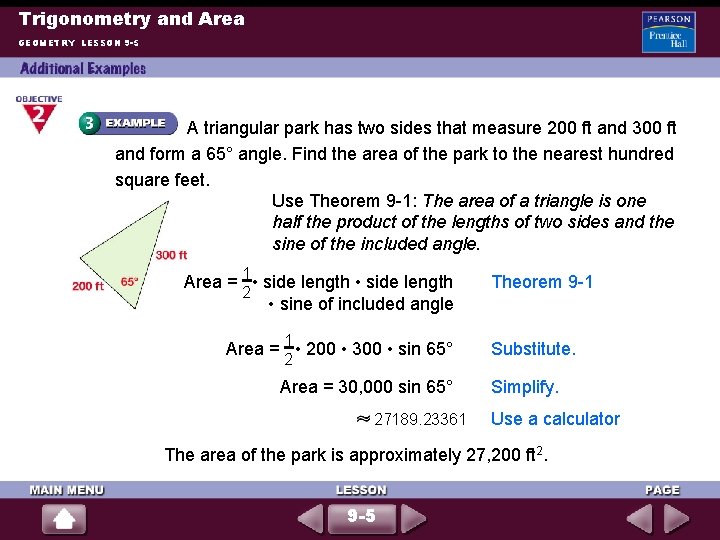
Trigonometry and Area GEOMETRY LESSON 9 -5 A triangular park has two sides that measure 200 ft and 300 ft and form a 65° angle. Find the area of the park to the nearest hundred square feet. Use Theorem 9 -1: The area of a triangle is one half the product of the lengths of two sides and the sine of the included angle. 1 Area = • side length 2 • sine of included angle 1 Area = • 200 • 300 • sin 65° 2 Area = 30, 000 sin 65° 27189. 23361 Theorem 9 -1 Substitute. Simplify. Use a calculator The area of the park is approximately 27, 200 ft 2. 9 -5

Trigonometry and Area GEOMETRY LESSON 9 -5 Pages 500 -503 Exercises 1. 173. 8 cm 2 5. (continued) e. about 58. 8 in. 2. 84. 3 in. 2 f. about 238 in. 2 3. 259. 8 m 2 12. 18. 0 ft 2 13. 7554. 0 m 2 14. 311. 3 km 2 6. 259. 8 ft 2 4. 2540. 5 yd 2 7. 47. 0 in. 2 5. a. 72 15. 151. 4 mm 2 16. 0. 7 ft 2 8. 1131. 4 cm 2 b. 36 17. 5523 yd 2 9. 8 ft 2 c. about 8. 1 in. 18. a. 50 mm 2 10. 151 m 2 d. about 11. 8 in. b. 116 mm 2 11. 27. 7 m 2 9 -5

Trigonometry and Area GEOMETRY LESSON 9 -5 19. Answers may vary. Sample: 1. Find the apothem and the side to the apothem using a 30 -60 -90 with hyp. 1. Then use the 1 formula A = ap. 2 2. After finding the apothem and the side, the height of the equil. is the apothem + 1. Then use the formula A= 1 bh 2 20. 1, 459, 000 ft 2 29. (area of pent. A) ≈ 1. 53 • (area of pent. B) 21. $51. 96 22. 20. 8 m; 20. 8 m 2 23. 45. 3 in. ; 128 in. 2 30. (area of hex. A) = (area of hex. B) 31. (area of oct. B) ≈ 1. 17 • (area of oct. A) 24. 17. 6 ft; 21. 4 ft 2 25. 42 cm; 127. 3 cm 2 32. (area of dec. A) = 0. 01 • (area of dec. B) 26. 61. 2 m; 282. 8 m 2 33. 5. 0 ft 2 27. 6. 2 mi; 3 mi 2 28. (area of sq. A) = 4 • (area of sq. B) 9 -5

Trigonometry and Area GEOMETRY LESSON 9 -5 34. a. Each central 34. (continued) measures (360 ÷ n) e. X tan(180/X) 1 and m C = 2 f. X increases by 1 that measure or and Y 1 (180 ÷ n). approaches . s b. tan C = = s 1 c. s = tan C, so p = n • 2(tan C) or 2 n(tan C). d. Since a = 1 and p = 2 n(tan C), A = 1 1 ap = (1) 2 2 (2 n tan C) = n(tan C) n tan 180 g. Answers may vary. Sample: 425; as X increases, Y 1 approaches , so the first 4 viewable decimal places become fixed; the n-gons n 9 -5 34. g. (continued) start to look like a circle of radius 1. 35. Using steps similar to Ex. 34, A = 180 n cos sin , n n which also appr. as n increases. 36. 320 ft

Trigonometry and Area GEOMETRY LESSON 9 -5 37. 0. 65 38. B 39. G 41. (continued) [1]Correct drawings OR correct solutions OR one correct drawing with solution 40. B 42. [4] a a. x = 54; tan 54° = 10 41. [2] so a = 10 tan 54° 13. 8 yd 42 sq. units, 24. 6 sq. units 42. [4] (continued) b. Use the formula 1 A= ap where A 2 represents the area, a represents the apothem, and p represents the perimeter. c. The perimeter is (20)(5), or 100 yd. A = 1 ap 1 2 A = 2 (10 tan 54°)(100) 688. 2 yd 2 9 -5

Trigonometry and Area GEOMETRY LESSON 9 -5 42. (continued) [3] appropriate methods, but with one computational error 43. – 2, – 9 44. 6, 1 45. – 6, – 1 46. – 2, – 2 and 4, – 2 [2] correct answer but with no work shown [1] correct answer to (a) 376 45 25 48. in. 2 4 63 2 49. m 8 47. cm 2 a 2 + 4 b 2 50. ; a , 0 2 a b 2 + b 2 51. ; a , 2 2 9 -5

Trigonometry and Area GEOMETRY LESSON 9 -5 Find the area of each figure. Give answers to the nearest unit. 1. regular hexagon with perimeter 90 ft 585 ft 2 2. regular pentagon with radius 12 m 342 m 2 3. regular polygon with 12 sides of length 1 in. 11 in 2 4. 5. 490 mm 2 70 yd 2 9 -5

Right Triangle Trigonometry GEOMETRY CHAPTER 9 Page 508 9. 41 8 57 1. 57 , , 10. 18. 7 11 11 8 33 4 2. 33 , , 4 7 7 17. 11. 9. 5 3. 48. 0 12. 28 sin x° = a 4. 28. 3 13. about 116 ft cos(90 – x)° = 5. 8. 9 14. about 710 m 6. 84. 9 15. about 31 ft It follows that sin x° = cos (90 – x)° by subst. 7. 36. 9 16. about 123. 7 mi; about 14° south of east 8. 5. 8 c 9 -A a c 18. 95, – 44 19. – 133, – 346

Right Triangle Trigonometry GEOMETRY CHAPTER 9 20. about 174. 9 mi/h at about 59° north of east 26. 22. 1 in 2 21. about 52. 2 mi at about 73° east of south 28. 86. 6 ft 2 27. 279. 1 mm 2 29. 21. 4 cm 2 22. 1, 8 23. 4, 1 24. 8. 1 mph at 39° north of west 25. Check students’ work. 9 -A